论Miller-Rabin算法预处理的局限性*

王景中，周 靖

(北方工业大学 信息与通信工程学院，北京100144)

论Miller-Rabin算法预处理的局限性*

王景中，周 靖

(北方工业大学 信息与通信工程学院，北京100144)

信息安全领域中极为重要的公钥密码体制的关键在于生成两个大素数，目前虽已有多项式运行时间的确定性素性检测算法AKS算法，可惜运行时间还达不到实用要求，故还是快速实用的概率性素性检测算法Miller-Rabin算法为主流，但其有一点一直被忽略——Miller-Rabin算法直接控制的其实是误判率而不是出错率，而后者才是真正需要降低的。对此做了详细分析，同时考察一些利用素数分布特性的预处理措施在降低出错率方面的效果，并分析了这一类优化的效果极限,否定了其必要性，相比之下，针对算法底层的优化更为直接有效。

素性检测;Miller-Rabin算法;误判率与出错率;素数分布;预处理的局限性;算法底层优化

0 引 言

目前，信息化已经成为社会发展的核心和潮流，信息是社会发展的一种非常重要的战略资源。因特网的发展，打破了传统的空间和地域的观念，从而实现了真正的全球信息化，然而由于网络的互联性、共享性和开发性，使得网络面临着信息的假冒、篡改和泄露等威胁。因此，随着互联网应用的不断广泛和深入的发展，信息安全的重要性亦越发凸显。

信息加密技术是保证网络中数据安全的最主要同时也是最基本的措施。在很多情况下，对网络中的数据进行加密是保证数据通信安全的唯一方法。在数据的加密过程中，需要使用各种加密算法来实现。另外，由于传输过程中存在数据被通信双方之外的第三方伪造或篡改的可能，通信双方无法验证数据来源，就很有可能出现一方抵赖的情况，此时就要求保证传输信息的不可否认性，数字签名就是通信双方在网上交换信息时，防止伪造和欺骗的一种身份认证技术。而公钥密码体制无论是在保密性还是鉴权认证方面都十分的实用和可靠，因而得到广泛的认同和应用。RSA目前已成为公钥密码的国际标准，其理论基础是数论中的一条重要论断：求两个大素数之积是容易的，而将一个具有大素数因子的合数进行分解却是非常困难的。显然大素数的选取是构造RSA密钥的关键[1-3]，为了保证安全性，一般产生素数是生成随机数然后对其进行素性检测，分为两类：确定性素性检测算法和概率性素性检测算法，前者不存在误判，但是运行都很慢，如AKS算法和APRCL算法[4-6]；后者存在一定的误判率，但可以被有效地控制到足够小，且运行速度较快，如Solovay-Strassen算法和Miller-Rabin算法[7-12]，其中Miller-Rabin算法更实用，但其有一点一直被忽略——Miller-Rabin算法直接控制的其实是误判率而不是出错率，以下将首先对此算法进行详细分析。

1 Miller-Rabin算法分析

为了后续的推导，首先不加证明地介绍如下4个引理及1个推论[7-9,13]：

引理1(Fermat小定理)：若n为大于2的素数，a为小于n的正整数，则an-1≡1(modn)。

引理2：若n为大于2的素数，则x2≡1(modn)的解满足x≡±1(modn)。

引理1、2推论：若n为大于2的素数，可令n-1=2sr，其中r为奇数，s为正整数，a为小于n的正整数，j为正整数且j≤s-1，则有ar≡1(modn)或存在j使得a2jr≡-1(modn)。

引理3：若n为大于2的素数，p,q为正整数,则xq-1≡1(modnp)的模n相异解的个数为gcd(q-1,(n-1)np-1)。

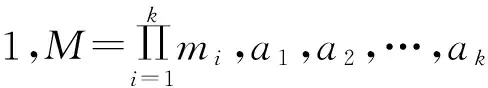
对模M有唯一解，且a1,a2,…,ak不完全相同时，解模M相异。

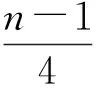
得证。

2 算法指标分析

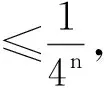
出错率与误判率其实是先验概率、后验概率的关系，这两者与随机选取数时选到一个素数的概率有关，不妨设其为p素，稍加分析可知：

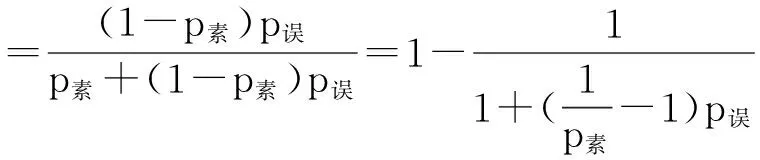
展开为级数得：

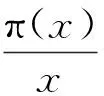
于是可以看出，要达到我们测试的真正目的，即降低p错，有两个方向：一是降低p误，简单地增加测试轮数即可；二是提高p素，这需要在随机抽取数n时采取一些策略，即预处理，根据素数分布特性，数越大素数越稀疏，因此合数拥有小素数因子的概率较大，故预处理时用一些小素数筛一下能较有效的滤除大部分合数，另外可采用递增随机法取数，即在一个大随机数的基础上，每次递增lnn附近的一个随机数的增量，因为这是素数的平均间距，从而更有可能选取到素数。然而这里仔细计算一下可以发现，明确了降低p错的目标之后，若以抵消掉p素的影响为要求，用第一种方法，只需要增加3、4轮测试即可达到要求，时间消耗增加约为7%，当然p素、p误的实际数值会影响这数据，但实际上，随着被测试数的增大，p素的减小十分缓慢，几乎不怎么需要额外增加测试轮数，例如被测试数从128位增加到256位后，还不需要增加额外的测试轮数，同时随着被测试数的增大，测试的标准轮数亦会相应增大，因此增加的时间消耗可能还会更低，不妨粗略定其为10%。再考虑预处理措施，无论如何p素是不可能被提高到1的，提高10倍几乎是其极限了，也就相当于额外增加1、2轮测试的效果，其时间额外消耗一般与额外测试轮数大致相当，至少节省的时间及其有限，然而算法的复杂性却提高了，带来了新的安全隐患。

相比之下，若对算法底层运算过程进行优化，不像预处理措施那样有理论上的很有限的优化效果上限，底层优化能够在效果不变时带来较大的时间节省，那么若利用节省的时间来增加测试轮数的话，就能在时间消耗不变的情况下，较大幅度的降低p误从而降低p错。至于算法底层优化则有较多方式，考虑到Miller-Rabin算法最为耗时的步骤在模幂操作和循环，常见的对算法的优化实现主要集中在对这两部分运算的优化。例如对模幂操作的优化可以使用改进的滑动窗口算法结合Montgomery模乘和模平方算法来改进其中的模乘操作，其中模乘算法如果采用大整数乘法和除法求模乘，因为涉及耗时的除法操作，所以要相对较慢，结合大整数乘法和Barrett求模算法可以用2(n2+3n+1)步单精度乘法完成。使用Montgomery求模算法结合大整数乘法算法，可以在2n(n+1)步单精度乘法内完成算法。Montgomery模平方的操作可以在3n(n+1)/2步单精度乘法内完成，而Barrett模平方需要(3n(n+3)/2+1)步单精度乘法。结合改进的滑动窗口算法和Montgomery类算法，可以得到目前非特殊情况下的较优的模幂算法。

表1给出模幂算法的比较，其中k是窗口大小，根据情况选择以达到最优，t是指数的二进制位数。

表1 模幂算法比较表

3 结 语

通过对Miller-Rabin算法的理论和性能的详细研究，发现若明确了降低p错的这个目标，则算法的预处理的优化效果还不如直接增加测试轮数，同时算法的复杂性提高带来了新的安全隐患，因此对Miller-Rabin算法的优化研究不应该再关注这一方面，相比之下，应该考虑算法底层实现过程中的优化，如针对其中模幂算法的优化，后者更为直接有效。

[1] 李荣森， 秦杰， 窦文华. RSA系列算法在工程中的应用研究[J]. 计算机科学，2007(34)： 86-90. LI Rong-sen, QIN Jie, DOU Wen-hua. Study on Implementing RSA Algorithm in Actual Project[J]. Computer Science, 2007( 34): 86-90.

[2] 陈作新. 一种基于AES和三素数RPrime RSA认证加密方案[J].计算机应用， 2008(28)： 3199-3201. CHEN Zuo-xin. New Authentication Encryption Schemebased on AES and Three-Prime RPrime RSA[J]. Journal of Computer Applications. 2008, 28: 3199-3201.

[3] 肖振久， 胡驰， 陈虹.四素数RSA数字签名算法的研究与实现[J].计算机应用， 2013(33):1374-1377. XIAO Zhenjiu, HU Chi, CHEN Hong. Research and Implementation of Four-Prime RSA Digital Signature Algorithm[J]. Journal of Computer Applications. 2013(33):1374-1377.

[4] MANINDRA AGRAWAL, NEERAJ KAYAL, NITIN SAXENA. Primes is in P[J]. Annals of Math. 2004(160): 781-793.

[5] BERRIZBEITIA P． Sharpening “Primes is in P”for a large family of numbers[J]. Math. Comp. 2005, 74(252): 2043-2059.

[6] 刘永亮， 姚鸿勋， 高文. AKS算法对现代密码学的影响[J].计算机工程与应用， 2003(11)： 0001-0003. LIU Yong-liang,YAO Hong-xun, GAO Wen. The Effect of AKS Algorithm on Modern Cryptography[J]. Computer Engineering and Applications, 2003(11):0001-03.

[7] YAN SONG YUAN. Number Theory for Computing[M].Berlin: Springer-Verlag, 2002.

[8] RABIN MICHAEL. Probabilistic Algorithmsfor Testing primality[J]. Journal of Number Theory. 1980(12):128-138.

[9] MONIER LOUIS. Evaluation and comparison of two efficient probabilistic primality testing algorithms[J]. TheoreticalComputer Science. 1980(12):97-108.

[10] BERNSTEIN J ．Proving Primality in Essentially Quartic Random Time[J]. Math. Comp. 2007, 76(257): 389-403.

[11] 杨波. 现代密码学[M]. 北京: 清华大学出版社, 2007. YANG Bo. Modern Cryptography[M].Beijing: Tsinghua University Press, 2007.

[12] 秦晓东, 辛运帏, 卢桂章. Miller_Rabin算法研究与优化实现[J]. 计算机工程, 2002(28): 55-57. QIN Xiao-dong, XIN Yun-wei, LU Guizhang. Research and Efficient Implementation of Miller-Rabin algorithm[J]. Computer Engineering, 2002,28: 55-57.

[13] RICHARD COURANT, HERBERT ROBBINS. What is Mathematics[M].London: Oxford University Press,2009.

National Natural Science Foundation Project(No.61371142)、Beijing innovation team building promotion plan(ID HT20130502)

Preprocessing Limit of Miller-Rabin Test

WANG Jing-zhong， ZHOU Jing

(Department of Information and Communication Engineering,North China University of Technology,Beijing 100144,China)

Public key cryptosystem is an extremely important part in information security field, and its key lies in generating two big primes. Nowadays, although there is polynomial-time definitive primality detecting algorithm, such as AKS algorithm, unfortunately its running time could not meet the practical demands, therefore, the fast and practical probabilistic primality testing algorithm, Miller-Rabin test, becomes the main algorithm. However, some detail of Miller-Rabin test is always ignored: it is misjudgment probability not error probability that is directly controlled by the test, while the latter is what indeed needs to decrease. Detailed analysis of this point is given, and meanwahile, the effects of some preprocessing methods with distribution features of primes to decrease error probability are tested. Finally, the optimized result limit is analyzed and its necessity negated. Comparison indicates that, the underlying optimization of algorithm is more effective.

primality test; Miller-Rabin test; misjudge probability and error probability; prime distribution; preprocessing limit; underlying optimization of algorithm

date:2014-10-05；Revised date：2015-02-27

国家自然基金项目(No.61371142)、北京市创新团队建设提升计划(No.ID HT20130502)

TP301.6

A

1002-0802(2015)04-0469-04

王景中(1962—)，男，硕士，教授，主要研究方向为数字图像处理及其应用、网络与信息安全；

周 靖(1990—)，男，硕士研究生，助研，主要研究方向为数字图像处理及其应用、网络与信息安全。

10.3969/j.issn.1002-0802.2015.04.017

2014-10-05；

2015-02-27