基于不同光源下的诱骗态双向QKD协议研究*
张昌宏,李 鹏
(1.海军工程大学 信息安全系,湖北 武汉 430033;2.中国人民解放军92886部队,山东 胶州 263000)
基于不同光源下的诱骗态双向QKD协议研究*
张昌宏1,李 鹏2
(1.海军工程大学 信息安全系,湖北 武汉 430033;2.中国人民解放军92886部队,山东 胶州 263000)
在量子密钥分配系统的光源特征研究中,通过实验分析了标记单光子源(HSPS)对基于诱骗态双向QKD协议系统安全性的影响。首先,基于诱骗态方法和双向QKD协议,给出使用HSPS的诱骗态双向QKD协议中单光子、双光子的计数率下限和误码率上限的计算公式;其次,计算出相应的安全密钥率公式;最后通过数值模拟,比较了不同光源下的诱骗态双向QKD协议的安全密钥率和安全传输距离,模拟结果表明HSPS光源相比WCP光源在安全密钥率和传输距离方面具有明显优势。
双向QKD;光源;诱骗态
0 引 言
密码的安全性由密码算法设计的科学性和密钥的保密性共同决定,如何使密码通信双方安全地获取密钥一直是信息安全领域关注热点。量子通信协议的建立,摆脱了传统密钥分配协议中加密协议部分在量子通信过程中不可使用的困境,在此基础上发展出的量子密钥分配协议在未来的保密通信中将发挥出越来越明显的技术优势。量子密钥分配(QKD,Quantum Key Distribution),是指以量子物理基本原理为核心,在量子通信系统的双方之间建立起无条件安全密钥的过程,其密钥分配方案通过将密钥信息编码在量子态中以确保密钥的安全性。1984年,Bennett和Brassard提出了著名的BB84协议[1],标志着量子密钥分配理论的逐渐成型,但在实用领域由于装置水平的限制等因素,量子通信的安全性仍然很难达到合理期望,因此,如何在通信双方之间的有效距离内形成较为安全的密钥成了研究的重点。近年来,诸如SARG04协议[2]、LM05协议[3]等一些基于参量下转换光子对的诱骗态(decoy state)方法的量子密钥方案相继被提出,相比于传统的BB84协议有了更为广阔的发展前景。
1 诱骗态量子密钥分配
1.1 光子数分束攻击
理想的量子通信的安全性已经被量子的物理特性所保证,但大多数协议的设计建立在单光子源的基础上。由于目前单光子源技术的不成熟,在实际QKD实验中,使用的多为强衰减的弱激光脉冲,而不是理想的单光子源,因此不可避免地会出现多光子的情况。特别是,单光子脉冲在传输信道中会受到各种衰减,经过一段距离后,多光子脉冲占据了剩余脉冲的主要地位,此时,窃听者Eve就可以通过光子数分束攻击(PNS),在通信双方Alice和Bob不知情的情况下利用多光子携带的相同信息特性,来获取Alice和Bob通信双方之间的密钥信息。而攻击者可以通过将单光子脉冲全部拦截后丢掉,不让其产生绝对安全的密钥。因此,考虑到光子数分束攻击的存在,传统的量子通信协议在非理想条件下的传输距离和安全密钥率都受到较大限制。
1.2 诱骗态方案
2003年,Hwang[4]提出了诱骗态方法,以更好地估计脉冲中的单光子比率,这使得QKD系统的安全密钥率和最大安全距离都有显著提升,并被证明是抵抗光子数分束攻击(PNS)的最佳方案[5]。诱骗态方法的基本原理是,发送方Alice分别制备信号态和诱骗态两种光子脉冲,这些冗余的诱骗态光脉冲与信号态光脉冲的唯一区别就是平均光强不同,根据不同强度下两种态的相位和偏振都是随机的特性,窃听者Eve在不知情的情况下,不能分辨出截获的信息是信号态光子还是诱骗态光子,只能对其完全接收。但接收方Bob通过对信号态和诱骗态分别进行计数,可以估计出信号态的单光子计数率下限和单光子误码率上限,最终可以得到诱骗态QKD协议的密钥生成率和安全通信距离。
这一方案的设计思想得到了学界的广泛认同,并出现了很多后续的改进方案。但总的来说,各个诱骗态协议具有的共同点,都是要设法在通信过程中利用不同光强下光源的不同特征,产生两种或两种以上的不同的光子数分布,借此对信道属性进行估计,通过观察光子数来测量是否有光子被窃取,最终得以判断是否存在窃听攻击。
1.3 LM05协议
LM05协议是一种典型的量子密钥分配方案,其具体工作流程如下:Bob在两种垂直偏振态、两种对角偏振态这四种偏振态中,选择一种光子态和两个基态(垂直偏振态)发送给Alice。与BB84协议类似,Alice利用控制模块以c的概率对其进行光子测量,这将保证这一部分光子至少会具有和BB84协议一样的安全性。而对于剩下的另一部分光子,Alice将以1-c的概率,通过对其进行翻转(编码为1)或不进行翻转(编码为0)进行编码,然后,Alice将处理后的光子发回给Bob,Bob通过其中相同的量子比特来准确地解码Alice的信息。可以看到,这种方法不需要经典信道,而是直接在量子信道之中进行通信,较以往的量子密钥分配协议,有了明显的突破。
需要指出的是,LM05协议并不能在信道被窃听或者有噪声时进行直接沟通。如果在其中使用纠错协议,窃听者Eve就会从中获取大量的信息,我们并不能确定这些信息是否会泄露密钥的相关信息;同样,如果在其中使用保密增强协议,Bob就不可能完全获得Alice的所有信息。目前而言,是否能够安全可靠地在有噪声或存在损失的信道中进行直接通信一直是众多协议中存在的瓶颈难题,但尽管如此,LM05协议仍是通过量子信道进行直接通信的卓有成效的方案。因此,本实验所使用的双向QKD协议即采用LM05协议。
2 基于不同光源下的诱骗态双向QKD协议分析
2.1 诱骗态双向QKD协议设计
一般诱骗态量子密钥分配的关键问题,是利用光脉冲检测得出安全的单光子计数率的下限和单光子误码率的上限,但由于双向QKD协议的设计,光子也会在双向信道的两次测量中出现损失。LM05协议中,采取了密钥提纯的方法并引入双光子计数率这一参数,有效减少了由于双向量子信道带来的部分损失,因此,本实验的设计采用LM05协议中的方法进行。
虽然,从理论上讲,无限诱骗态的方法更便于计算而且能更精确地研究不同光源下对其不同的干扰,然而,对于一个实用装置,其有限性是一个不可能改变的现实,因此,本文采用双诱骗态的方法,考虑分别用光强度为v1,v2下的两个诱骗态和光强度为μ下的一个信号态进行实验,其中v1+v2<μ且v1+v2<1。这些条件并不意味着对μ值的约束,仅仅是为了确保其最大密钥率,并可以在实验中观察Qv1,Qv2两个诱骗态增益和Qu信号态增益。
由于理想的单光子源是理想QKD协议安全性的基础,但其制备过程在实际使用中非常困难,因此在应用环境下,当前实验使用弱相干光源(WCP)和标记单光子源(HSPS)近似代替理想单光子源。
2.2 基于WCP光源下的诱骗态双向QKD分析
2.2.1 单光子和双光子单独计数
实验采纳SARG04协议中的方法对双光子探测概率进行计算,但由于单光子计数率下限Y1本身不能直接在实验中测量,而只能估计其下限,因此,首先需要对单光子的探测概率进行公式推导。记单光子计数率下限的形式为:
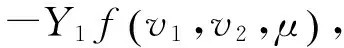
记在光强度v1,v2下的两个诱骗态的增益分别为Qv1,Qv2,误码率分别为e1,e2,可以建立关于增益和误码率的方程:
(1)
(2)
假设在光源发射的脉冲中,不含有大于2的光子数的光脉冲,则式(2)可化简为:
(3)
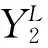
(4)

对于双光子脉冲计数率的计算,由于实验围绕光脉冲中单光子和双光子计数率展开,因此,可以对式(2)右边的第二项进行改写,令其为:
(5)
由此可得:
(6)
式(6)中,Y0的取值参考文献[6]的计算值:
(7)
这里,存在以下不等式:
(8)
(9)

(10)
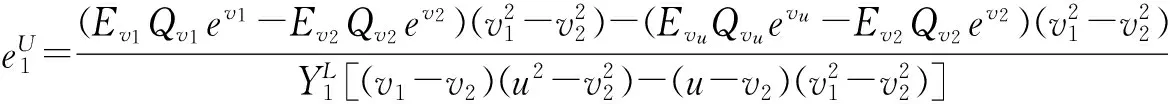
(11)
2.2.2 单光子和双光子整体计数
以上分析仅考虑单光子双光子计数率的准确性,但现实中由于探测装置只能探测到光脉冲的有无,却无法得知其确切的光子数。同时,由于信道干扰,无法完全根据Y1和Y2的函数关系确定接收到的究竟是单光子还是双光子,因此本节的计算,将把Y1和Y2当作一个整体来观察其在LM05协议中密钥生成率下界的变化,并期望得到一个下界为Y1+Y2的函数。由于:
(12)
(13)
(14)
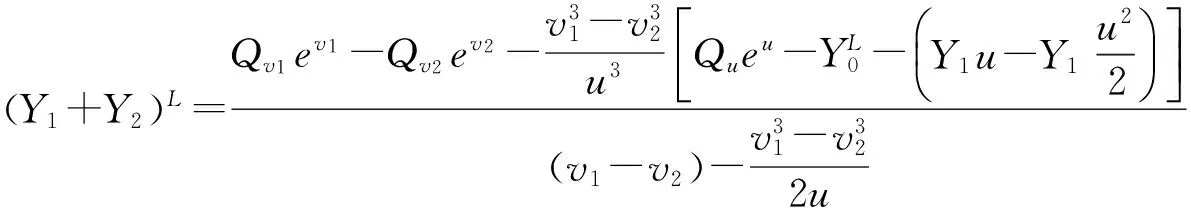
(15)
同样,以考虑Y1+Y2整体增益这种方式,可得Y1+Y2下界的有效增益为:
(16)
考虑到实际传输时存在于信道中的误码率,假设所有误码差均来自单光子和双光子检测(以及暗计数),可以得出:
EuQu=e0Y0e-u+εQ12(u)
(17)
式中,ε是有效误差的有效临界增益。最后,可以得到误码率的上限为:
(18)
2.3 基于HSPS光源的诱骗态双向QKD分析
2.2节在基于WPC相干光源的情况下对双向QKD协议进行了分析讨论,本节将在基于HSPS光源的情况下对双向QKD协议进行分析对比。由于二者的区别仅仅在于光子数分布不同,因此,仅需计算出在光子数分布不同的情况下,HSPS标记单光子引起的新的计数率和误码率的不同即可。
HSPS光源一般由单模自发参量转换触发机制产生,其产生的光子数分布如下式所示:
(19)
接收方Bob接受检测到的第i个光子态的增益,可以用指数函数表示为:
(20)
同时,可以计算出第i个光子态的量子比特误码率(QBER)为:
(21)
经过整理,可以得到HSPS光源的总误码率为:
(22)
同2.2节的方法一样,通过建立增益与误码率关系的方程,可以求得光子计数率的下限。首先,可计算增益为:
(23)
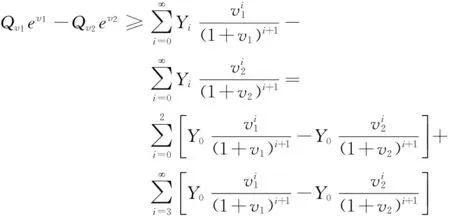
(24)
通过整理上式,可以得到基于HSPS光源下单光子、双光子计数率下限为:
(25)
(26)
在此列出增益与误码率的相关方程:
(27)
(29)
2.4 安全密钥率
在安全密钥率的计算上,文献[7]只涉及到单光子计数的安全密钥率,但在双光子态保密放大不超过单光子态的情况下,该框架可以被扩展到包括双光子计数率的情况。因此,可以用2.3节中得到的公式,通过GLLP公式[7]来推导它们的安全密钥率:
(30)
综合上述单独计数和整体计数的方法,得出其各自的安全密钥率为:
(31)
(32)
需要说明的是,本实验出于保密性能放大的要求,需从单光子和双光子贡献相结合的角度确定有效的误码率,因此,实验舍弃这两个比特数中较大的数值,以确保Eve窃取的信息量没有被低估。量子比特的取舍参考文献[8]中的公式:
(33)
3 实验结果
根据HSPS的诱骗态双向QKD协议中单光子、双光子计数率的下限和在误码率上限的计算公式和相应的安全密钥率公式,通过Matlab软件进行数值模拟,可以得到使用不同光源的诱骗态双向QKD协议的安全密钥率和安全传输距离。为了数值计算的方便,实验中统一采用弱+真空的诱骗态协议,令其中的一个光源强度无限趋近于0。在不考虑各种光强统计涨落的情况下,由于光纤在不同入射波长信号光作用下表现出不同的特性,光纤和探测器的具体数据选用如下的实验参数。

表1 光纤、探测器实验参数取值
首先,对上节两种不同计数方法得出的R1+2和R12安全密钥率作比较。图1中,1线标注处为80 km,2线R1+2代表使用单双光子单独计数时,WCP光源的安全密钥率随传输距离变化的曲线,3线R12代表使用单双光子统一计数时,WCP光源的安全密钥率随传输距离变化的曲线。显然,R1+2无论是距离还是安全性都高于R12。
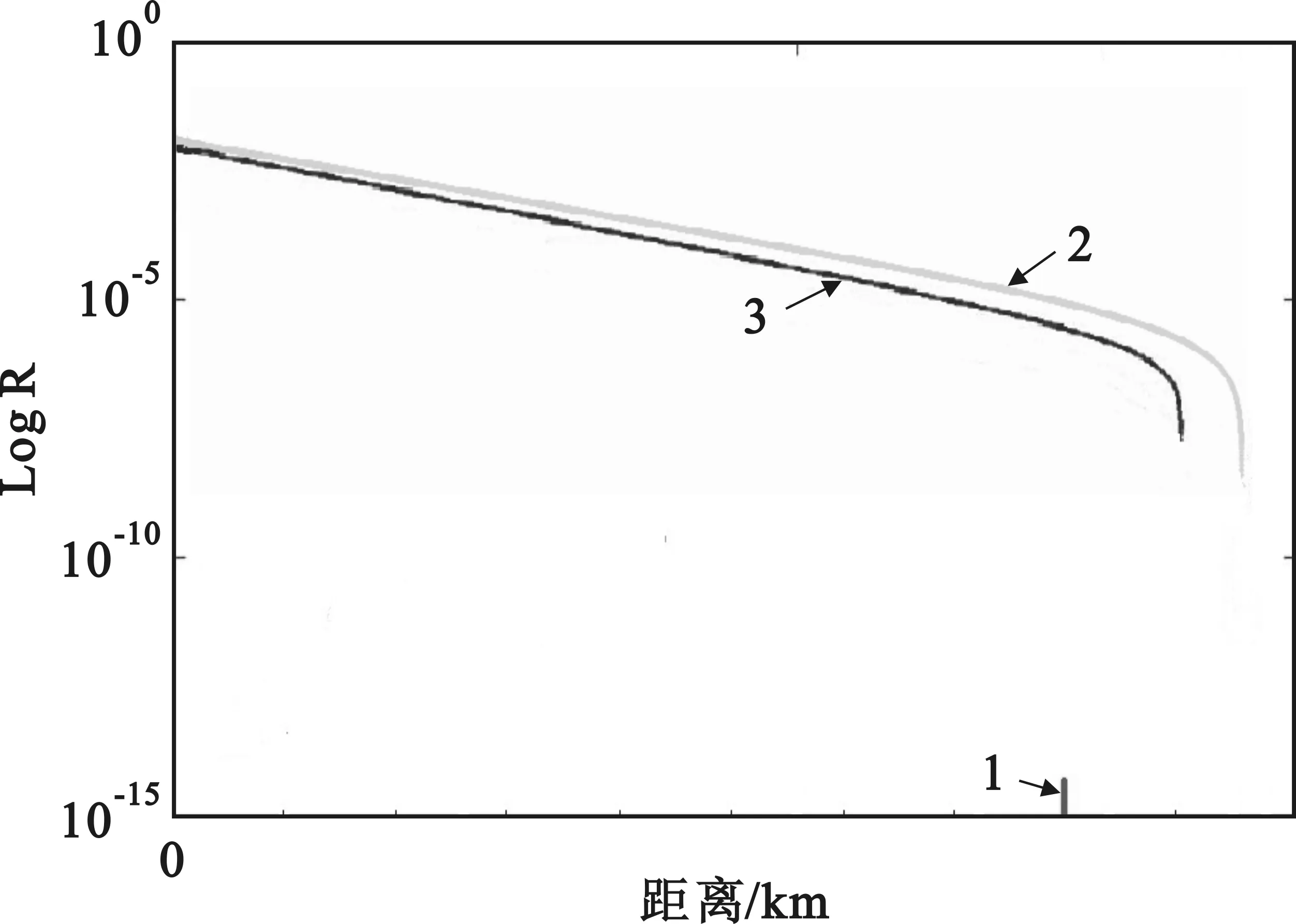
图1 单双光子单独计数与统一计数的密钥安全率曲线
接下来,将WCP相干光源在双向QKD(LM05协议)下安全密钥率R1+2随距离变化曲线,与传统WCP相干光源在普通QKD(BB84协议)下的曲线进行比较。图2中,1线标注处为80 km,在使用单双光子单独计数时,2线R1+2代表WCP光源在双向QKD下的安全密钥率随传输距离变化的曲线,3线代表WCP光源在普通诱骗态QKD下的安全密钥率随传输距离变化的曲线。
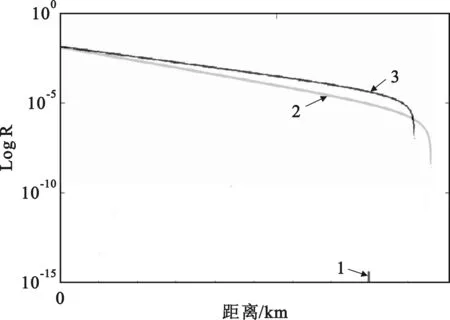
图2 WCP光源在双向QKD和普通QKD下的安全密钥率曲线
由图2可知,在传统BB84协议有效的安全密钥率范围内,双向QKD协议并没有优势,在一定的传输距离内,LM05协议使用的密钥率较BB84协议存在较低的安全性。但同时能够看到,虽然安全密钥率较低,但双向QKD协议延长了有效的通信距离。因此可以认为,在长距离(大于90 km)通信时,双向QKD协议较之传统的单向诱骗态协议具有优势。
最后,在基于双向QKD协议的条件之下,实验比较WCP和HSPS两种光源产生的密钥率的变化。图3中,1线标注处为80 km,在使用单双光子单独计数的条件下,2线为WCP光源的安全密钥率随传输距离变化的曲线,3线为HSPS光源的安全密钥率随传输距离变化的曲线。
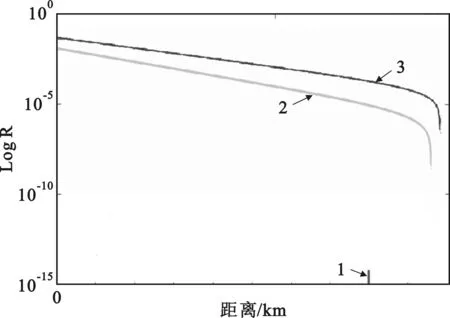
图3 WCP光源和HSPS光源的安全密钥率曲线
由图3可知,HSPS相比WCP,对此协议具有更好的适应性和安全性。通过将图2、图3对比可以发现,使用HSPS光源可以极大地扩展双向QKD协议的传输距离。因此,相比传统QKD协议,双向诱骗态QKD协议在传输距离方面有着明显的优势,在保证一定安全性的基础之上,未来研究的重心可以放在如何增大传输距离方面。模拟结果证明:HSPS光源相比WCP光源在双向诱骗态协议中,在安全密钥率和传输距离方面具有明显优势。
[1] Bennett C H, Brassard G. Quantum Cryptography: Public Key Distribution and Coin Tossing [J]. Theoretical Computer Science, 2014,560(1):7-19.
[2] Scarani, Acin A, Ribordy G. Quantum Cryptography Protocols Robust against Photon Number Splitting Attacks for Weak Laser Pulse Implementations [J]. Physical review letters,2004,20(6):119-124.
[3] Kwong H,Chau H F, Ardehali M. Efficient Quantum Key Distribution Scheme and a Proof of Its Unconditional Security [J]. Journal of Cryptology , 2005,18:133-140.
[4] Hwang W Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication [J]. Physical Review Letters,2003,91(5):97-99.
[5] 唐少杰.量子通信中单光子源特性的研究[D].北京:北京邮电大学,2011. TANG Shao-jie.The Charatieristic Study of Single Photon Source in Quantum Communication[D].Beijing:BUPT,2001.
[6] Shaari J S, Bahari I,Ali S. Decoy States and Two Way Quantum Key Distribution Schemes Optics Communications[J]. Optics Communications,2011,284(2): 697-702.
[7] Gottesman, Lutkenhaus H K. Security of Quantum Key Distribution with Imperfect Devices[J]. Information Theory, 2004(06):27-33.
[8] Kwong H. Practical Decoy State for Quantum Key Distribution[J]. Virtual Journal of Quantum Information ,2005(07):46-55.
Decoy State Two-Way QKD Protocol under Different Light Sources
ZHANG Chang-hong1,LI Peng2
(1.Department of Information Security,Navy University of Engineering, Wuhan Hubei 430033, China;2.PLA Unit,92886; Jiaozhou Shandong 263000, China )
In the research on light source characteristics of QKD (Quantum Key Distribution) system, the effects of HSPS on the system sucurity based on the two-way QKD protocols of decoy state are analyzed. Firstly, the formula for lower and upper limits of the counting rate is given in the single-photon and two-photon case under the basis of decoy state method and two-way QKD protocols. Then, the formula of appropriate security key rate is calculated. Finally, through numerical modeling, the secure key rate and transmission distance are compared in different sources of decoy state two-way QKD protocol. Simulation result shows that HSPS enjoys obvious advantages over WCP in both secure key rate and transmission distance.
two-way QKD; light source; decoy state
date:2014-10-22;Revised date:2015-02-28
TP393
A
1002-0802(2015)04-0463-06
张昌宏(1964—),男,硕士,副教授,主要研究方向为信息安全;
李 鹏(1986—),男,硕士,助理工程师,主要研究方向为信息安全。
10.3969/j.issn.1002-0802.2015.04.016
2014-10-22;
2015-02-28

