WSN中节点定位方法的改进*

马淑丽，赵建平，张炳婷，盛艳梅，陈 丽

(曲阜师范大学 物理工程学院,山东 曲阜 273165 )

WSN中节点定位方法的改进*

马淑丽，赵建平，张炳婷，盛艳梅，陈 丽

(曲阜师范大学 物理工程学院,山东 曲阜 273165 )

无线传感器网络节点位置信息的获取非常关键。首先考虑节点分布问题提出了一种新的节点分布模式，并改进定位算法，将节点定位过程主要分为一级定位和二级定位。一级定位采用基于优先值阈值的质心定位算法，并将一级定位的节点作为新锚节点参与二级定位。二级定位使用基于优先值阈值的DV-Hop最小二乘定位算法。Matlab仿真结果证明，提出的节点分布模式利于节点定位，一级定位算法降低了计算量，并与二级定位算法一起提高了定位精度。

节点定位；DV-Hop；最小二乘法；质心定位法

0 引 言

无线传感器网络(WSN，Wireless Sensor Network)传感器节点通常部署在人不能长时间滞留的环境中，由于成本原因传感器节点只有少数带有GPS或北斗等定位装置。节点定位根据已知节点位置信息求未知节点位置，方法主要分为两大类：一是基于测距的节点定位方法，定位精度高，但硬件成本、通信量、计算量高[1]；二是无需测距定位方法，成本低，定位精度低，能满足一般粗精度定位的应用。无需测距的定位算法包括 DV-Hop、质心定位法、凸规划定位算法、Amorphous定位算法、APIT算法、AHLos算法、N-Hop Multilateration Primitive算法、SeRLoc算法等[1]。本文主要研究并改进DV-Hop定位算法和质心定位算法。

1 典型定位算法概述

1.1 DV-Hop算法

DV-Hop定位算法是由美国罗格斯大学(Rutgers University)Dragos Niculescu等人提出的6种分布式定位算法之一[1]。主要分为4个过程：1.锚节点以泛洪的方式广播位置信息和初始跳数值0，每被转发一次跳数值加1。接收节点只保留每个锚节点最小的跳数值，最终得每个节点间的最小跳数。2.根据已知的锚节点位置信息计算锚节点间平均每一跳的距离如式(1)，并将其作为校正值广播。

(1)

式中，xi，yi是锚节点i坐标值，xj，yj是锚节点j坐标值，hij是锚节点i、j间的最小跳数，dHopi是锚节点i到其他锚节点的平均每一跳距离。3.未知节点到每个锚节点的跳数分别乘以与之最小跳数锚节点的校正值，得到未知节点与每个锚节点间的估算距离。4.利用最小二乘法或三边测距等定位方法计算未知节点坐标。

1.2 最小二乘法原理

为了使节点定位误差降到最低，需满足下式[2]

(2)

式中，n是锚节点个数，x，y是未知节点真实坐标值，di是未知节点与锚节点i间的估算距离。根据以下式子，利用最小二乘法最终估算出未知节点坐标：

(3)

将式(3)前(n-1)个方程分别减去第n个方程得：

AX=b

(4)

(5)

(6)

(7)

1.3 质心定位算法

质心定位算法由南加利福尼亚大学(University of Southern California)Nirupama Bulusu等人提出[1]，是将未知节点定位在锚节点的几何中心的定位方法如下式：

(8)

式中，(x，y)是未知节点坐标，xi，yi是未知节点通信范围内的锚节点i的坐标值，n是未知节点通信范围内锚节点个数。

质心定位算法计算量比DV-Hop算法计算量小，不需要广播信息得到所有跳数值和广播校正值，降低了无线传感器网络能量消耗。但其定位精度依赖于节点分布的均匀性。

1.4 其他概念

绝对误差：指未知节点估测坐标与实际坐标距离，一般作为节点的定位误差。定位精度：平均定位误差与节点通信半径的比率值，值越小定位精度越高。

2 改进的节点定位方法

2.1 改进节点分布模式

对于节点定位算法的研究首先要根据实际应用建立节点分布环境模型。许多文献如文献[3]采用未知节点与锚节点随机均匀分布的仿真环境如图1所示。

图1 文献[3]节点分布

为了更进一步提高节点定位精度，本文提出了锚节点完全均匀分布，其他节点随机均匀分布的仿真环境。将监控区域划分为m(4、9、16等)个相同的小几何区域，在每个小区域的几何中心放置1个锚节点。如图2所示。

图2 本文节点分布图m=9

2.2 改进节点定位方法

文献[4]提出一种按优先级定位节点的方法，并将先定位的节点升级为锚节点后再进行下一级定位的方法，直到所有节点定位完成，提高了定位精度。但是该方法定位分为多次进行，每次都采用改进的DV-Hop算法，节点广播信息次数多，会增加节点的能量消耗[5]。本文提出二级节点定位，第一级采用优先值阈值的质心节点定位方法，第二级将第一级定位节点升级为锚节点后采用优先值阈值的DV-Hop定位算法定位。剩余未定位节点(少量)可通过DV-Hop定位，或使用优先值阈值的DV-Hop再进行分级定位。比文献[4]降低了计算量与泛洪次数，减少了节点能量消耗。

2.3 基于优先值阈值的质心定位

文献[3]采用基于加权的质心定位方法，提高了定位精度，但是需要进行(n-2)次三边测量计算，最后根据加权质心法定位节点，计算量大。本文一级定位采用优先值阈值的质心定位方法：每个未知节点都有自己的优先值，未知节点每检测到1个与之一跳距离的锚节点，优先值加1。当优先值大于阈值时，未知节点参与定位。将参与一级定位的未知节点一跳距离的锚节点位置信息代入式(8)，求出未知节点坐标，并升级为新锚节点参与下一级节点定位。比文献[3]计算量降低。

2.4 基于优先值阈值的DV-HOP定位

新锚节点广播位置信息和初始跳数值0。二级未知节点优先值更新，优先值大于二级阈值的参与二级定位。根据锚节点位置信息与新锚节点的估算位置信息求出二级锚节点平均每跳距离，广播校正值。二级未知节点计算出与每个锚节点间的距离di。将与二级定位未知节点有一跳距离的锚节点位置信息代入式(3)中的相应方程，用最小二乘法估算每个二级节点坐标。

3 仿真结果分析

3.1 仿真环境验证

在边长为100 m的正方形区域分布109个节点并编号，其中9个锚节点的编号从1到9，未知节点的编号从10到109。节点通信半径30 m。文献[3]的仿真环境中所有节点随机均匀分布，本文仿真环境将其中9个锚节点分布在9个小正方形区域的几何中心，其他节点与文献[3]未知节点分布相同。用DV-Hop算法定位本文与文献[3]仿真环境中的未知节点，并对两种环境下节点定位误差进行比较，如图3所示。

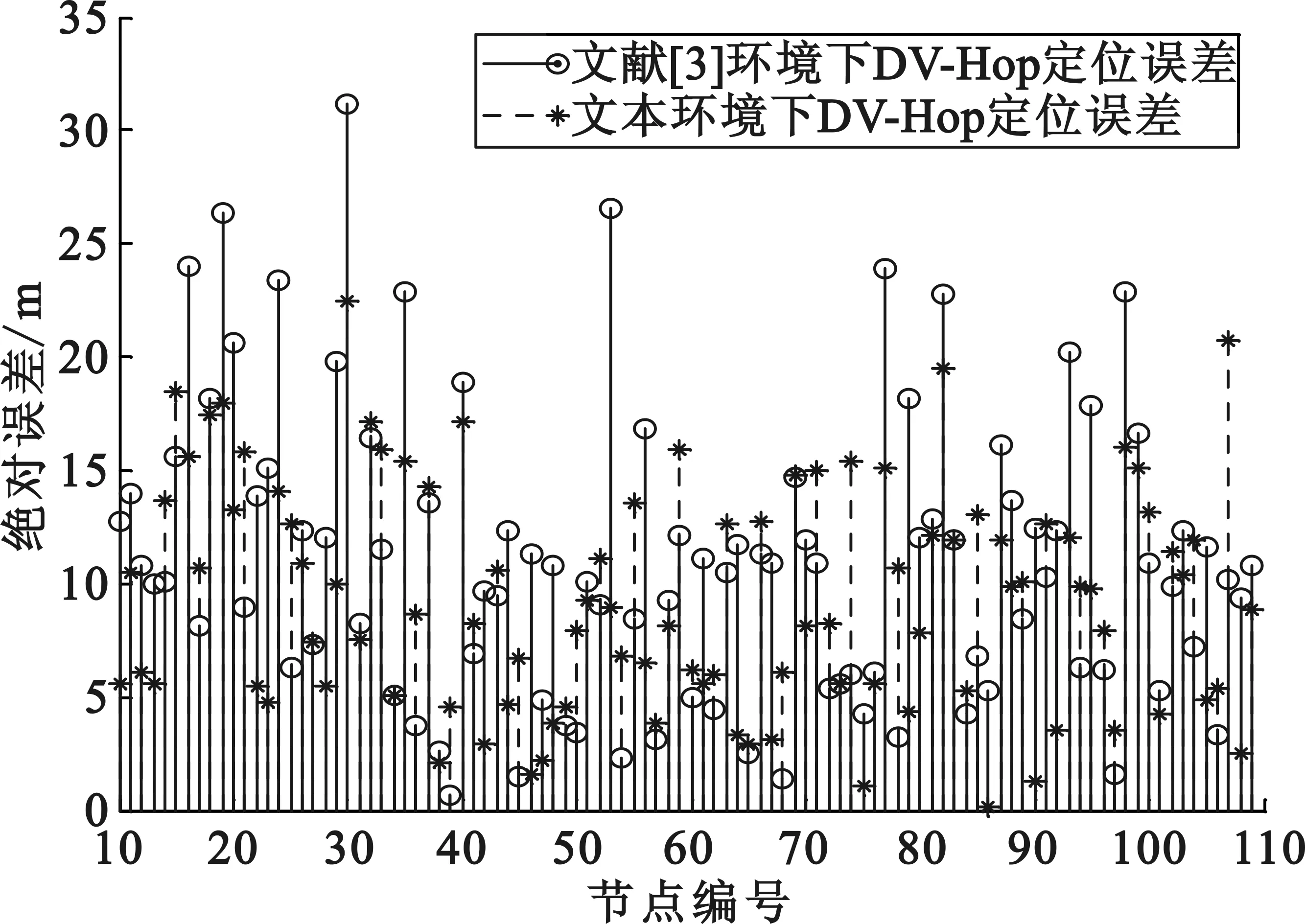
图3 两种环境下DV-Hop定位误差对比

仿真80次，在本文提出的的节点分布环境下定位精度为33%，比在文献[3]节点分布环境下定位精度提高约5.3%。证明本文提出的节点分布方法有利于提高DV-Hop算法定位精度。

3.2 一级基于优先值阈值的质心定位

未知节点通信范围内锚节点个数大于等于3时质心定位才有一定准确度。本文一级阈值设为3。将本文一级定位算法与文献[4]一级定位算法和DV-Hop算法在本文环境中仿真定位，并进行一级定位节点误差对比，如图4所示。

图4 本文一级定位、DV-Hop、文献[4]算法定位误差对比

仿真100次，本文算法一级定位精度15%，比文献[4]一级定位算法和DV-Hop算法分别提高约10%、11%。一级定位节点个数占总节点个数8%。

3.3 二级基于优先值阈值的DV-HOP定位

二级定位采用基于优先值阈值的DV-Hop最小二乘法定位。二级阈值取1到11的整数，分别进行100次仿真并与DV-Hop算法对比。当二级阈值为2、3时，本文算法二级定位精度分别提高约2%、3%，如图5所示。

图5 本文二级定位与DV-Hop定位精度对比

3.4 二级基于优先值阈值的质心定位

本文将二级定位方法改为基于优先值阈值的质心定位法进行仿真，并将一、二级定位精度与DV-Hop算法对比，如图6所示。

图6 两种定位算法对比

随着二级阈值增大，一、二级基于优先值阈值质心算法定位精度逐渐提高。当阈值达到8时开始定位精度比DV-Hop定位精度高，但是定位节点率低。

3.5 一级、二级基于优先值阈值定位

将本文一级基于优先值阈值的质心定位、二级基于优先值阈值的DV-HOP定位算法的定位精度与DV-Hop相应的节点定位精度对比，如图7所示。仿真证明本文提出的分级定位算法比DV-Hop算法定位精度高。二级阈值为9时，本文算法相应节点定位精度比原算法定位精度高9%。

图7 本文一、二级定位与DV-Hop定位精度对比

一、二级定位精度提高的同时，定位节点个数下降。二级阈值越大，二级定位节点个数越少。二级阈值为1时，一、二级节点定位率达85%，定位精度比DV-Hop高2%；二级阈值为2时，一、二级节点定位率达70%，定位精度比DV-Hop高3.7%。二级阈值从5开始越大需要的一级节点定位个数越多，如图8所示。

图8 定位节点个数与二级阈值关系

4 结 语

本文节点分布模式能提高DV-Hop定位精度5.3%，但增加了人力负担。本文模式中一级算法与文献[3]加权质心算法相比，降低了计算量并提高10%定位精度，与DV-Hop算法相比，提高11%。本文模式中：二级优先DV-Hop算法，在阈值为2、3时与DV-Hop算法相比，定位精度分别提高2%、3%；二级优先质心算法，在阈值为9到11的整数时，定位精度比DV-Hop算法提升，但是牺牲二级定位节点数。本文一、二级方法与DV-Hop算法在相同模式下，提高了定位精度，比文献[4]分多轮算法减少了泛洪次数，降低了节点能耗。本文定位方法能满足一般二维WSN应用，缺点是定位节点率达不到100%。下一步将改进的方法应用到三维仿真验证。

[1] 陈敏，王擘，李军华.无线传感器网络原理与实践[M].北京：化学工业出版社，2011. CHEN Min, WANG Bo, LI Jun-hua. Wireless Sensor Network Theory and Practice [M]. Beijing: Chemical Industry Press, 2011.

[2] 张是，李德敏，张晓露.基于ZIGBEE的自适应动态区域误差因子算法[J].通信技术，2014,2(47):179-183. ZHANG Shi, LI Min-de, ZHANG Xiao-lu. Adaptive Dynamic Regional Error Factor Algorithm based on ZIGBEE [J]. Communications Technology, 2014,2 (47): 179-183.

[3] 夏少波，连丽君，王鲁娜等.基于DV-Hop定位算法的改进[J].计算机应用，2014,34(05)：1247-1250. XIA Shao-bo, LIAN Li-jun, WANG Lu-na, et al.Improved DV-Hop Localization Algorithm[J]. Computer Application,2014,34 (05): 1247-1250.

[4] 杨石磊，樊晓平，刘少强等.一种改进的无线传感器网络DV-Hop定位算法[J].智能仪表与传感器，2008,16(09)：1356-1358. YANG Shi-lei, FAN Xiao-ping, LIU Shao-qiang, et al.An Improved DV-Hop Positioning Algorithm for Wireless Sensor Networks [J]. Intelligent Instruments And Sensors, 2008,16 (09): 1356-1358.

[5] (德)达尔吉,(美)玻尔拉伯尔.无线传感器网络基础理论与实践[M].孙利民等译.北京：清华大学出版社，2014. Dargie W(Germany),Poellabaure C(America). The Wireless Sensor Network Basic Theory and Practice [M]. SUN M L Translation. Tsinghua University Press, 2014.

Supported by the science and technology project of higher education of Shandong province(No.J12LN08);National Natural Science Foundation of China(No.11302118)

Improvement of Node Locating Algorithm in WSN

MA Shu-li，ZHAO Jian-ping，ZHANG Bing-ting，SHENG Yan-mei，CHEN Li

(College of Physics Engineering ，Qufu Normal University ， Qufu Shandon 273165，China )

It is of great importance to acquire the node location information of wireless sensor network. Firstly, for the problem of node distribution, a novel node distribution model is proposed, and the locating algorithm modified. Meanwhile,the node locating process is divided into first-stage locating and second-stage locating. The first-stage locating adopts centroid locating algorithm based on priority threshold, with its node as a new anchor node participating in the second-stage locating,while the second-stage locating uses DV-Hop locating algorithm based on least square priority threshold. Matlab simulation results show that the proposed node distribution model could facilitate node locating, the first-stage locating algorithm could reduce the amount of calculation and together with the second-stage locating algorithm,improve the locating precision.

node locating; DV-Hop; least square method; centroid locating algorithm

date:2014-10-09；Revised date：2014-02-17

山东省高等学校科技计划项目资助(No.J12LN08)；国家自然科学基金资助项目(No.11302118)

TP393

A

1002-0802(2015)04-0453-05

马淑丽(1989-)，女，硕士研究生，主要研究方向为无线传感器网络、无线通信技术;

赵建平(1964-)，男，教授，主要研究方向为无线通信技术;

张炳婷(1990-)，女，硕士研究生，主要研究方向为无线通信技术;

盛艳梅(1991-)，女，硕士研究生，主要研究方向为智能信息处理;

陈 丽(1990-)，女，硕士研究生，主要研究方向为光纤通信。

10.3969/j.issn.1002-0802.2015.04.014

2014-10-09；

2015-02-17