基于Logistic混沌序列的错误图样对纠错码的影响*

郝天铎，王可人，金 虎，熊 最

(电子工程学院，安徽 合肥 230037)

基于Logistic混沌序列的错误图样对纠错码的影响*

郝天铎，王可人，金 虎，熊 最

(电子工程学院，安徽 合肥 230037)

为了在“比特级”层面对纠错码进行更深入的研究，提出了一种服从Logistic混沌序列的错误图样分布模型。通过将混沌序列映射成二进制序列，并采用一定的方法使序列中“1”的数目可控，以此来生成错误图样。将卷积码、RS码以及RS+卷积级联码作为研究对象，以随机错误为参照，分别研究了该错误图样下三者的译码性能。仿真结果表明，基于Logistic混沌序列的错误图样对卷积码和级联码的影响要大于随机错误图样，而随机错误图样对RS码的影响更大。

Logistic混沌序列；错误图样；卷积码；RS码；级联码

0 引 言

在现代通信系统中，信道编码是提高信息传输可靠性的一种重要手段，被广泛应用在数字通信的各个领域中[1]。目前，研究纠错码性能的文章较多，但大多集中在编译码算法的改进和纠错能力的研究[2-3]，很少有人从“比特级”层面上进行更深入的分析。为了进一步研究纠错码的译码性能，本文从错误图样的角度出发，通过选择不同的错误图样，分析不同错误图样对纠错码译码的影响，从而建立一个纠错码对不同错误图样敏感性分析的数据集合。通过对众多错误图样进行研究，一方面，可以将信道当中的噪声和干扰等效为某种错误图样分布类型，并针对该错误图样类型选择纠错性能较好的信道编码进行通信；另一方面，虽然信道中对某种纠错码影响较大的错误图样出现的概率很小，但如果敌方正好利用这种错误图样对我方进行干扰，我方必须能够快速做出反应。因此，本文的研究不仅为通信系统的可靠性保障提供了一种可行的实施方案，在通信对抗领域的比特信息对抗领域也具有一定的参考价值。

在这样的背景下，由于混沌信号具有表明的伪随机性、非周期性、相关特性等一系列特殊的性质[4]，同时 Logistic混沌映射具有类似白噪声的功率谱[5]，因此，通过数学建模，将Logistic混沌信号作为干扰噪声转化到二进制序列，并作为错误图样对纠错码进行分析，未尝不是一个好的尝试。由于常用的Logistic量化函数[6-7]在映射时只能产生“0”和“1”均匀分布的二进制序列，这并不能满足错误图样中对“1”的比例实现可控的要求。因此本文在量化函数的基础上提出了一种新的映射方法，产生输入误比特率可控的错误图样，并在该错误图样下对卷积码、RS码和RS+卷积码的译码性能进行分析。

1 纠错码译码性能分析

1.1 错误图样简介

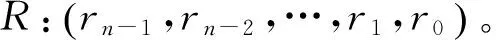
1.2 译码性能分析

对某一给定的(n,k,m)卷积码，假定p是二进制对称信道的比特差错概率，当p远小于1时，可以求得Viterbi译码器的输出误比特率Pec：

(1)

式中，df是卷积码的自由距离，Bdf是所有重量为df的路径的非零信息位总数[8]。

对某一给定的(N，K，M)RS系统码，假定ps是M进制对称无记忆信道的符号差错概率，当ps远小于1时，输出误码率为[9]：

(2)

式中，t为RS码可以纠正的差错符号上限。

对于RS(N，K，M)码+(n，k，m)卷积串行级联码而言，两者结合起来相当于码长Nn、信息位Kk、码率为Kk/Nn的分组长码。两者结合起来相当于码长Nn、信息位Kk、码率的分组长码，采用的信道为二进制对称信道(BSC)，假定p是二进制对称信道的比特差错概率，当p远小于1时，可以求得译码器的输出误码率Pers-c[10]：

(3)

2 基于Logistic混沌序列的错误图样模型建立

2.1 预备知识

Logistic混沌映射是一维混沌映射的主要方式，是混沌系统中被广泛研究的简单动力系统,可以根据它来产生伪混沌序列，其迭代方程为[11]：

(4)

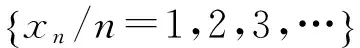
2.2 错误图样的参数设定

本文中错误图样分布由不同的参数所决定，如图1所示，在错误图样e中，Block代表“块”，在文中为产生错误的块的长度，pos为错误产生的首位置，亦即错误图样中首次出现“1”的位置，Ne为块内错误比特，D为两块之间的间隔，第一块内为随机错误，第二块内为突发错误。错误比特所在位置用“1”表示，空白位置用“0”表示。两个块的长度均为7 bit，第一块内“1”出现的次数为3，所以产生的是Ne1等于3 bit的随机错误；第二块内“1”出现的次数为7，所以产生的是Ne2等于7 bit的突发错误，错误图样中两个块之间的间隔D为3 bit。因此，错误图样e为：(10100100001111111)。

图1 错误图样e的不同参数示例

2.3 模型建立

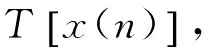
(5)

然而，如果将这种序列当做错误图样进行研究，会导致输入误比特率只能保持在0.5左右，无法对纠错码的译码性能进行有效研究，因此，在此基础上，本文提出了一种可以使“1”的数目可控的二进制序列映射方法。具体实施步骤如下：

第一步：通过公式(4)产生N个Logistic混沌序列值；

第二步： 根据实际情况设定输入误比特率的值p，也即二进制序列中“1”的个数errnum与序列总长度N的比值errnum/N；

第三步：对第一步所产生的序列值进行遍历，按照从小到大的顺序进行排列，并找出每一个序列值在原序列中所对应的位置pos(i)，若序列值大小相等，则pos(i)按照从前到后的顺序依次取值；

第四步：生成一个1行N列的全零序列，令其等于错误图样E；

第五步：在错误图样E中，令pos(1),pos(2),…pos(errnum)这些位置的值等于1，将Logistic混沌序列映射为错误图样E。

通过Matlab仿真实验分析，结果显示出本文方法产生的二进制序列与式(5)产生的序列的自相关性相同，具有一定的伪随机性，且在不同的初始值下，该二进制序列的变化很大，符合了混沌序列对初值敏感性的最根本特性，因此，可以认为所产生的序列是符合混沌特性的。由于篇幅所限，仿真图就不再列出。

由于混沌过程对初始值x1极为敏感，所以不同的初始值x1就会生成差异较大的Logistic混沌序列值，从而产生差距较大错误图样。因此，在接下来的分析过程中，以初始值x1为变量，探讨基于Logistic混沌序列的错误图样分布对卷积码、RS码及其级联码译码性能的影响；当x1一定时，再以输入误比特率为变量，对三种不同的错误图样分布下的纠错码译码性能进行仿真分析。

2.4 系统模型

本文只在“比特级”层面研究错误图样对其译码性能的影响，不考虑调制解调的作用，且假定在信道内，错误图样与所要传输的信息序列在叠加时是可以实现精确同步的。信道为二进制(或多进制)的对称无记忆信道，所研究的纠错码包括卷积码、RS码以及RS+卷积串行级联码，具体模型如图2所示。

图2 系统模型

3 仿真分析

由于在仿真时需要进行大量的重复随机性实验，所以仿真时采用蒙特卡罗仿真方法，如无特别说明，仿真次数一律设为10 000次。

3.1 对卷积码译码性能的影响

以(2,1,7)卷积码作为研究对象，译码方式采用硬判决下的Viterbi译码算法，设输入码长为10 000 bit，经编码后的码长为20 000 bit，则Logistic混沌序列长度N也应为20 000，分支参数μ=4，输入误比特率分别设为0.03、0.05、0.07和0.1，初始值x1从0.01到0.99并且以0.01为步径依次变化，测试不同初始值下基于Logistic混沌序列的错误图样对Viterbi译码性能的影响，仿真结果如图3所示。

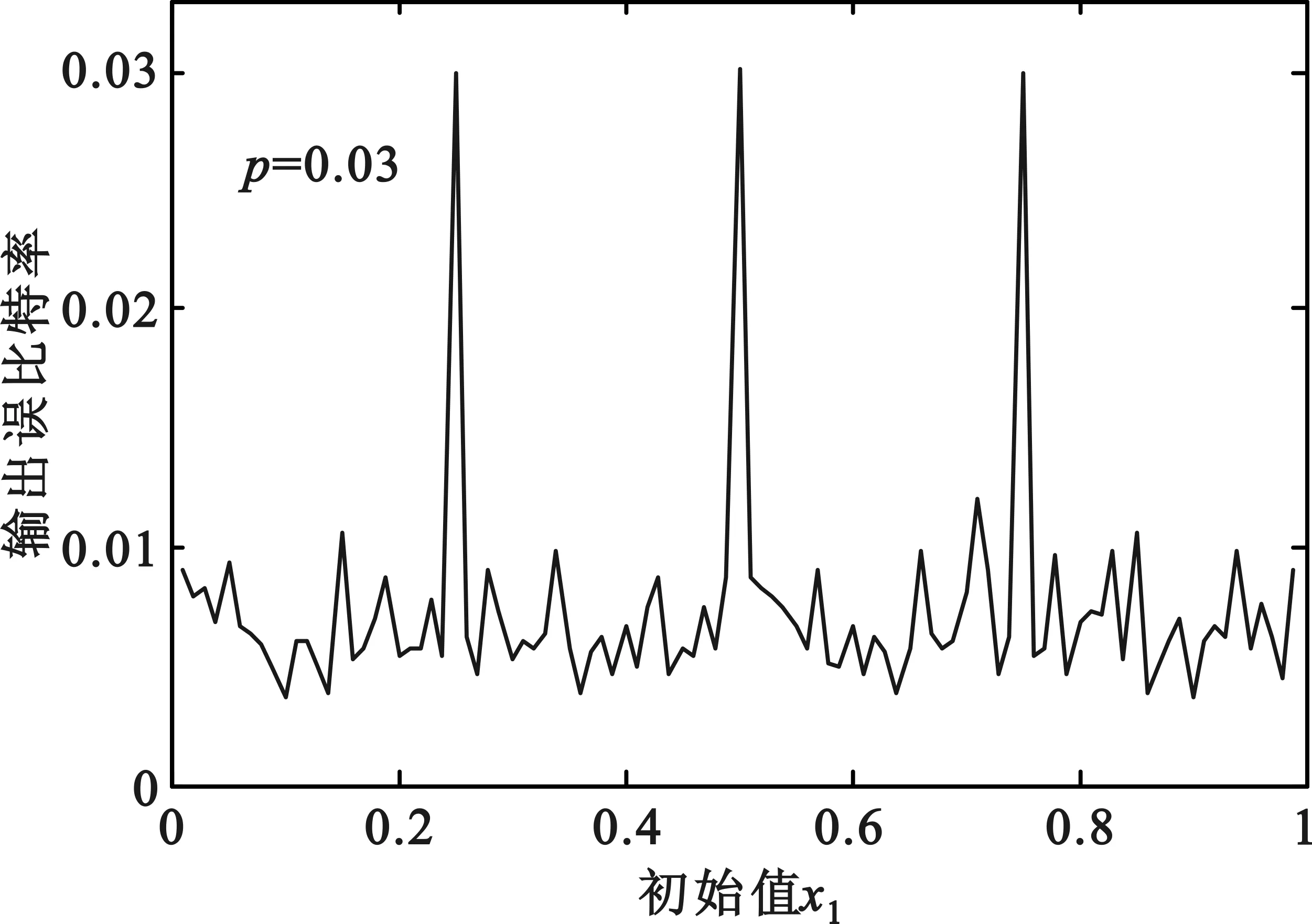
(a)输入误比特率为0.03时的性能分析

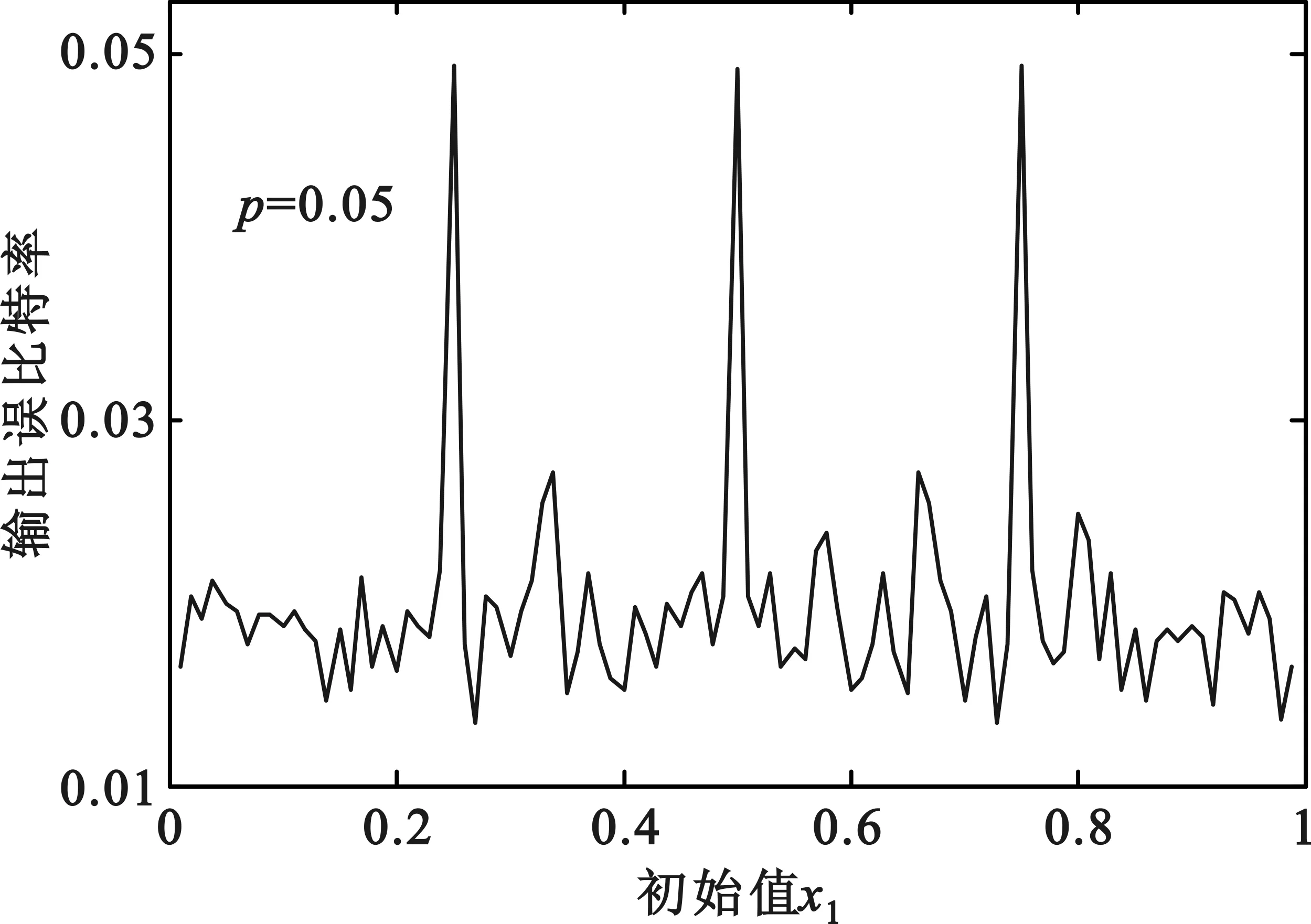
(b)输入误比特率为0.05时的性能分析

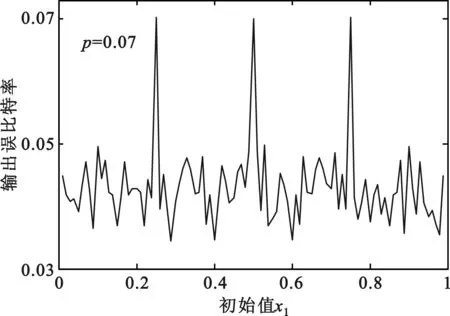
(c)输入误比特率为0.07时的性能分析

(a)输入误比特率为0.1时的性能分析

图3给出了4种不同输入误比特率下Logistic混沌序列的初始值对卷积码译码性能的影响。可以看出，不同初始值对卷积码的译码性能影响不同，但其输出误比特率的波动范围一般不超过0.03，这是因为初始值x1的选定对混沌序列影响极大，不同的初始值将产生差异较大的序列值，从而对基于Logistic混沌序列的错误图样也产生影响。当初始值取0.25,0.5和0.75的时候，图3(a)、图3(b)、图3(c)中的输出误比特率取到最大值，而图4(d)中的输出误比特率也取到极大值。这是因为当x1等于0.25、0.5和0.75时，通过式(4)生成的所有序列值几乎都相等，从而使产生的错误图样变为突发错误。

随着输入误比特率的变化，卷积码对随机错误图样和基于Logistic混沌序列的错误图样的敏感性分析比较如图4所示。其中，设输入误比特率从0.01到0.2变化，混沌序列的初始值取分别设为0.2，0.5和0.7。

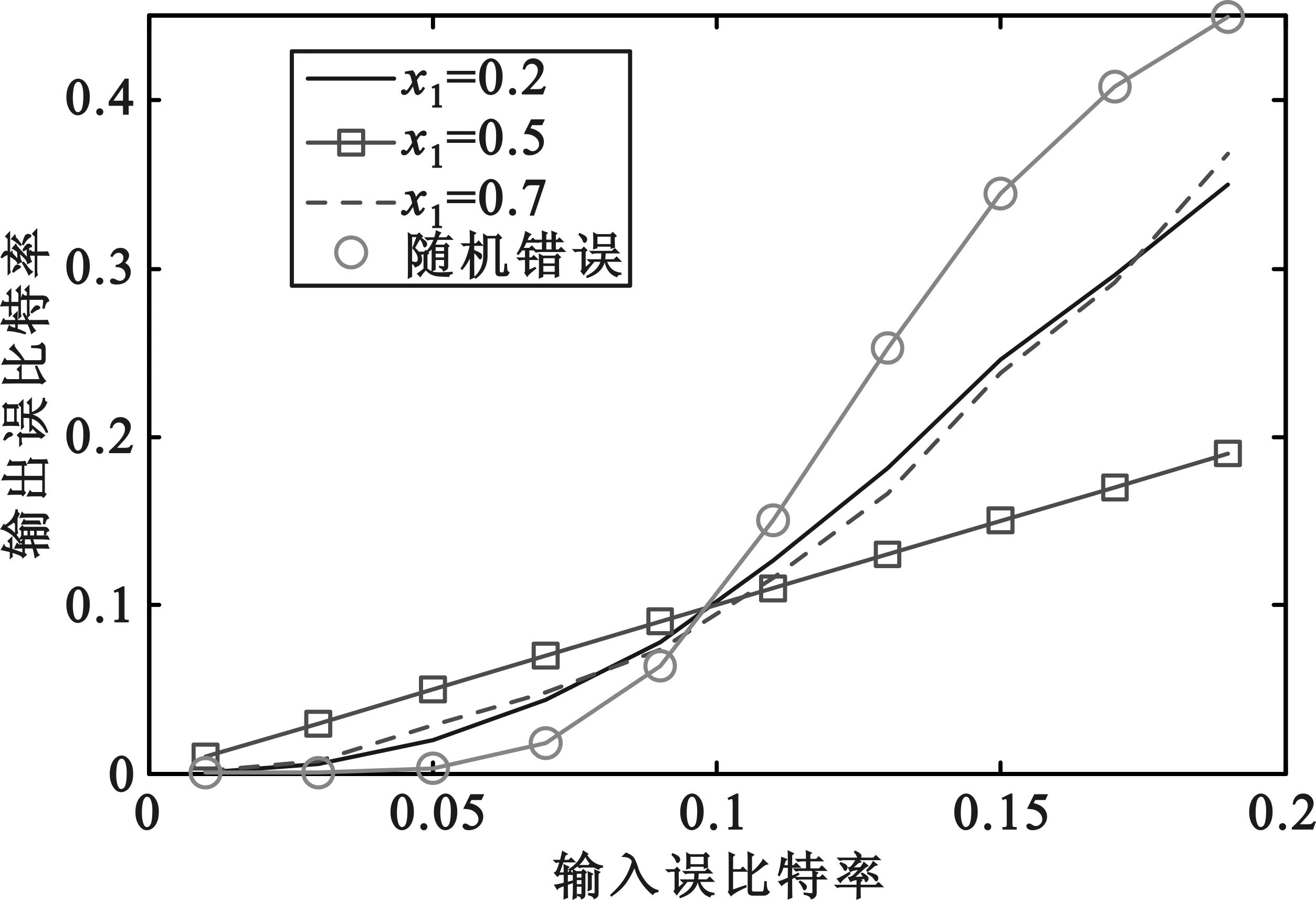
图4 基于Logistic混沌序列的错误图样与随机错误图样比较

从图4可以看出，当输入误比特率小于0.05时，卷积码对随机错误的纠错能力较强；当输入误比特率小于0.1时，卷积码对基于Logistic混沌序列的错误图样更为敏感，且不同初始值下的输出误比特率波动范围不超过0.03；当输入误比特率大于0.1时，此时卷积码对随机错误会产生越纠越错的现象，从而使错误扩散，导致输出误比特率迅速增大。当初始值等于0.5时，错误图样为突发错误，输出误比特率与输入误比特率呈正比关系。

3.2 对RS码译码性能的影响

以(255,223)系统码为研究对象，设输入码序列长为1 000帧，经编码后的码长为2 040 000 bit，则相应的产生长度N为2 040 000的Logistic混沌序列，以初始值x1为变量，分析不同输入误比特率下基于Logistic混沌序列的错误图样对RS码译码性能的影响，结果如图5所示。

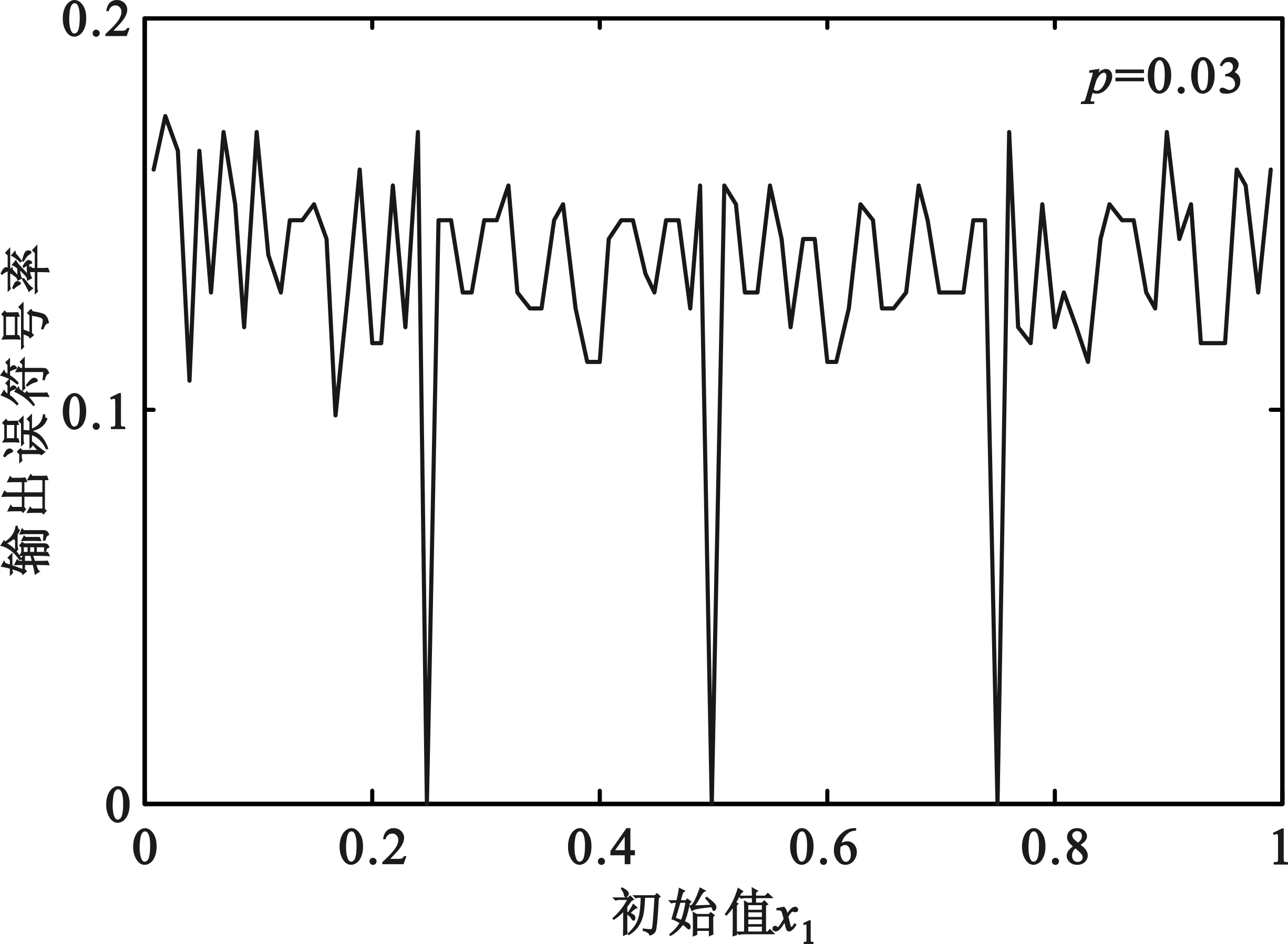
(a)输入误比特率为0.03时的性能分析

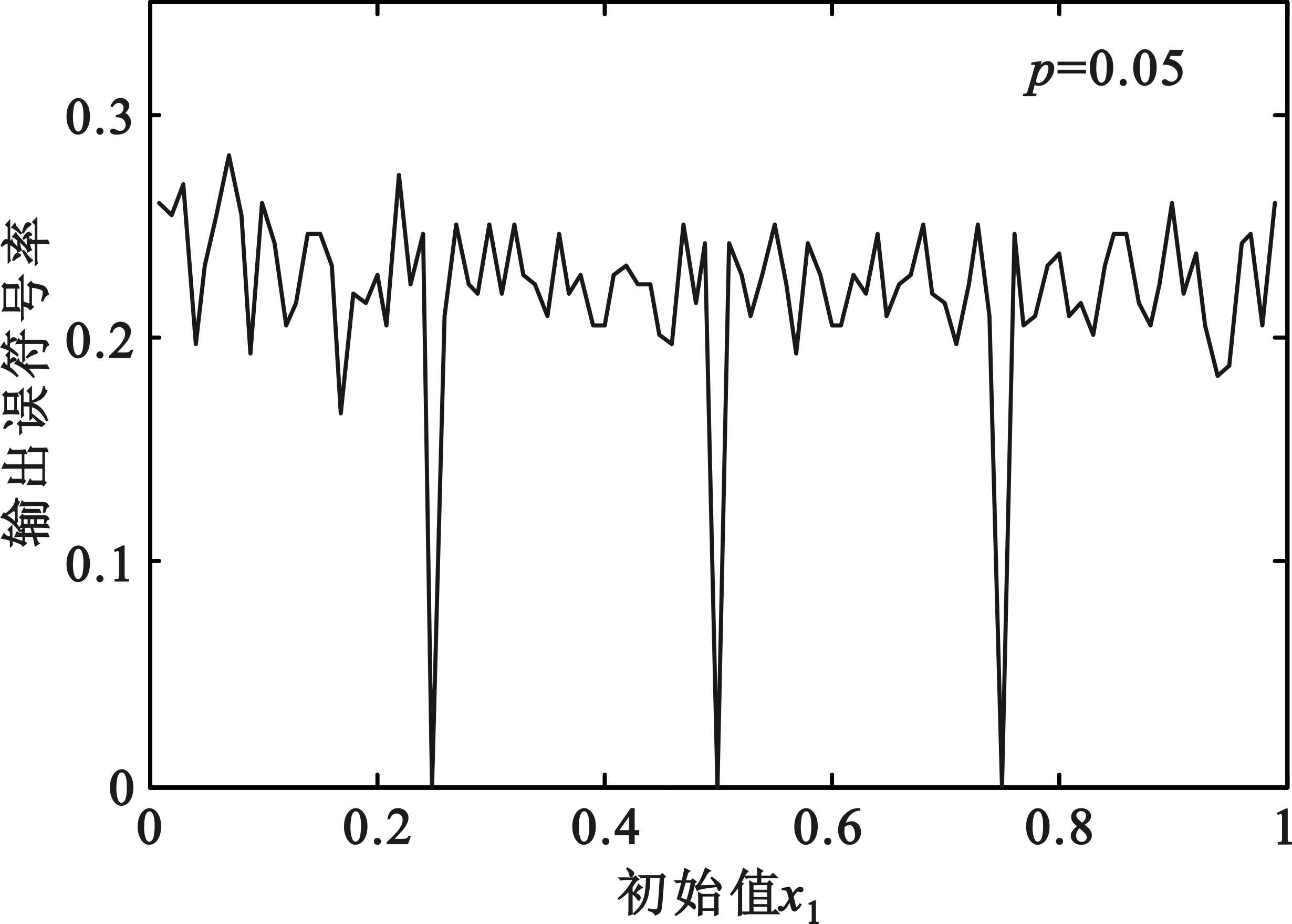
(b)输入误比特率为0.05时的性能分析

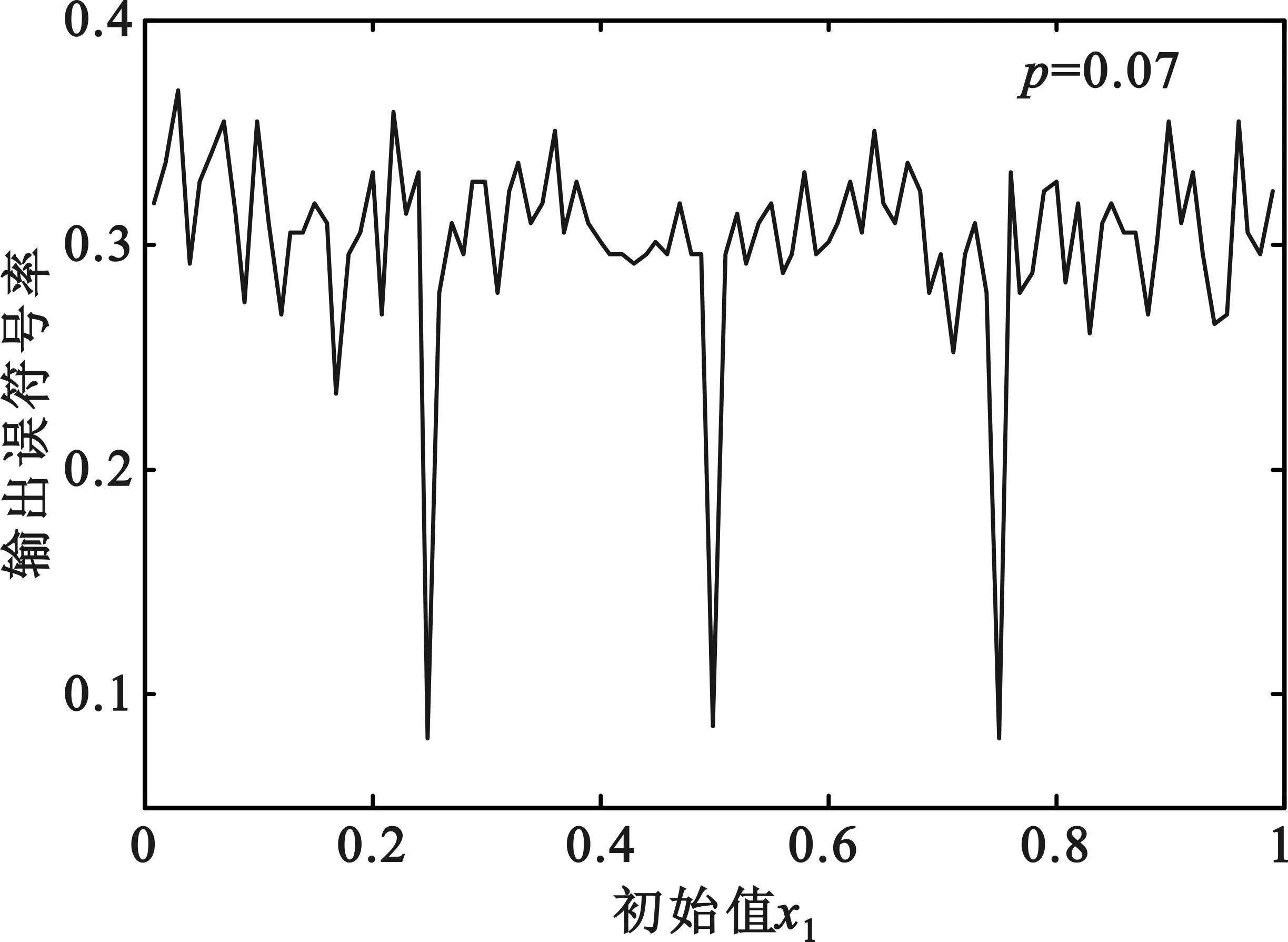
(c)输入误比特率为0.07时的性能分析

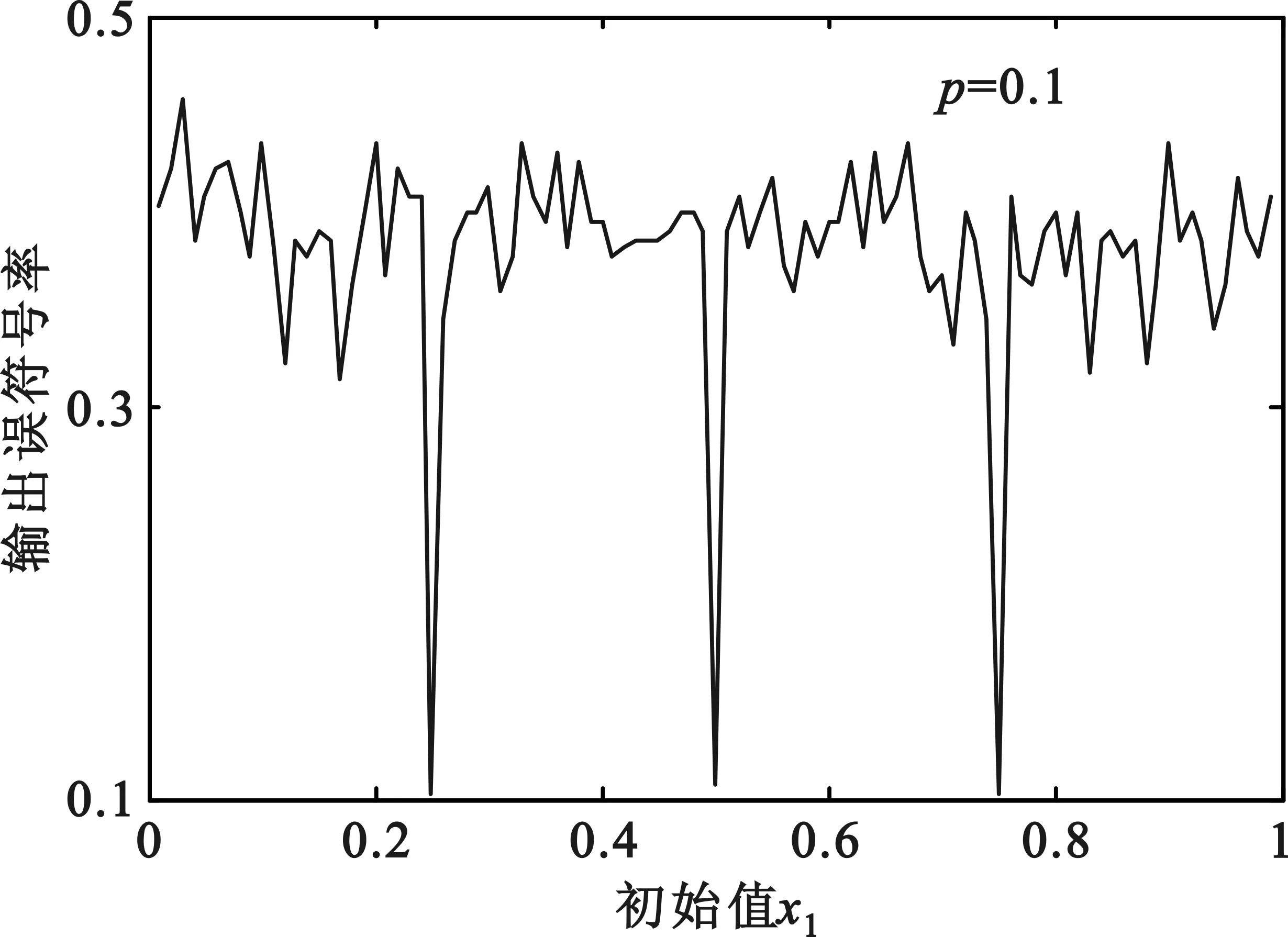
(d)输入误比特率为0.1时的性能分析

从图5可以看出，不同初始值对RS码的译码性能影响不同，当初始值取0.25，0.5和0.75时，4种输入误比特率下的输出误符号率都达到最小，这是因为此时的错误图样正好是突发错误，且RS码对突发错误的纠错能力较强；除了这三个初始值外，其他初始值对RS的译码性能影响相差不大，输出误符号率的波动范围很小。令一方面，当输入误比特率不同时，图5中的4个图的波形变化趋势却十分相似，这说明RS码对初始值的敏感性并不会受到输入误比特率的影响。

随着输入误比特率的变化，RS码对随机错误图样和基于Logistic混沌序列的错误图样的敏感性分析比较如图6所示。其中，设输入误比特率从0.01到0.2变化，混沌序列的初始值取分别设为0.2，0.5和0.7。

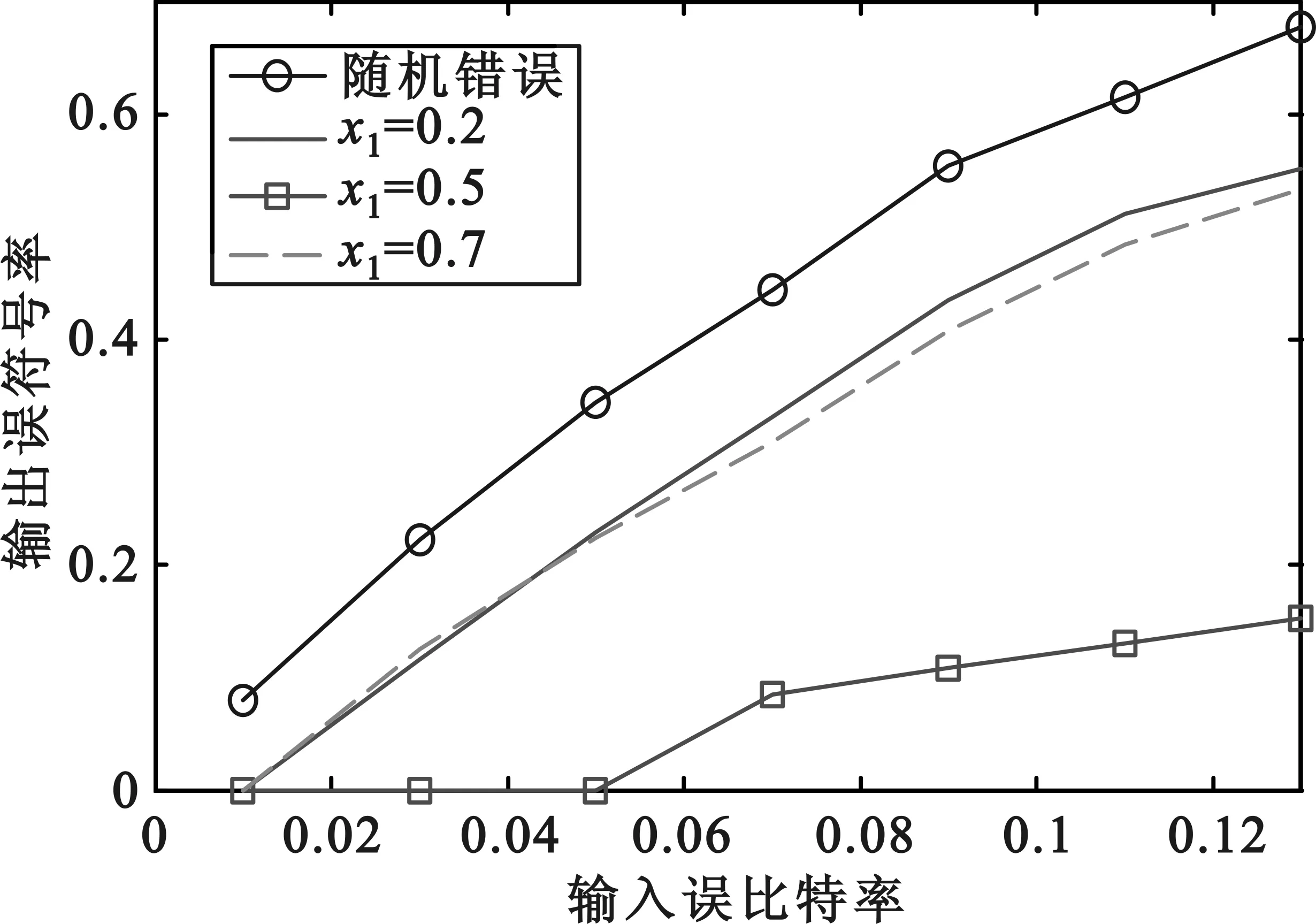
图6 基于Logistic混沌序列的错误图样与随机错误图样的比较

从图6可以看出，RS码对随机错误的敏感性较大，这是因为在同样的输入误比特率下，随机比特错误更有可能产生相对较多的输入错误符号。对基于Logistic混沌序列的错误图样而言，当初始值x1=0.2或0.7时，由于此时的错误图样按一定的规律分布，所以产生的输入错误符号要小于随机错误图样的错误符号，因而对RS码影响要小于随机错误；又根据图5的分析，大部分初始值对译码的影响差别不大，所以这两条曲线的走向也很接近。然而，当初始值等于0.5时，错误图样就变为突发错误，此时产生的输入错误符号是最少的，因而RS码对该初始值下的错误图样具有较强的纠错能力。

3.3 对RS+卷积级联码译码性能的影响

选择RS(255,223)+卷积(2,1,7)级联码为研究对象[12]，输入码序列设为1 000帧，则相应的产生长度N为4 080 000的Logistic混沌序列。以初始值x1为变量，探讨不同输入误比特率下基于Logistic混沌序列的错误图样对RS+卷积级联码译码性能的影响，结果如图7所示。

从图7可以看出，当初始值取0.25，0.5和0.75时，图7(a)、图7(b)两幅图的输出误符号率达到最大，而图7(c)、图7(d)两幅图的输出误符号率达到最小，对比图3和图5的仿真结果，可以说明当输入误比特率较小时，卷积码对基于Logistic混沌序列的错误图样起主要纠错作用；当输入误比特率较大时，RS码对该错误图样起主要纠错作用。

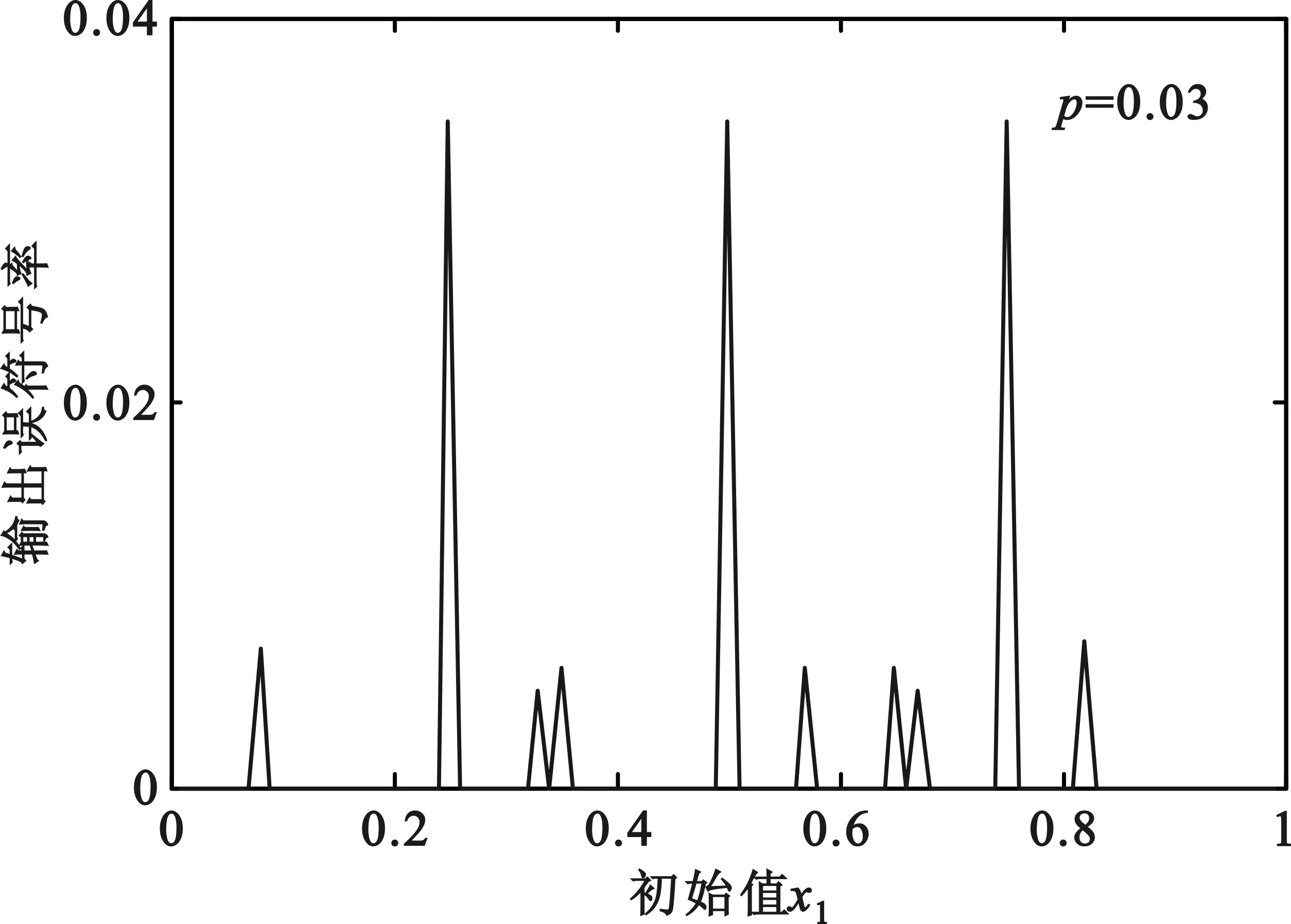
(a)输入误比特率为0.03时的性能分析

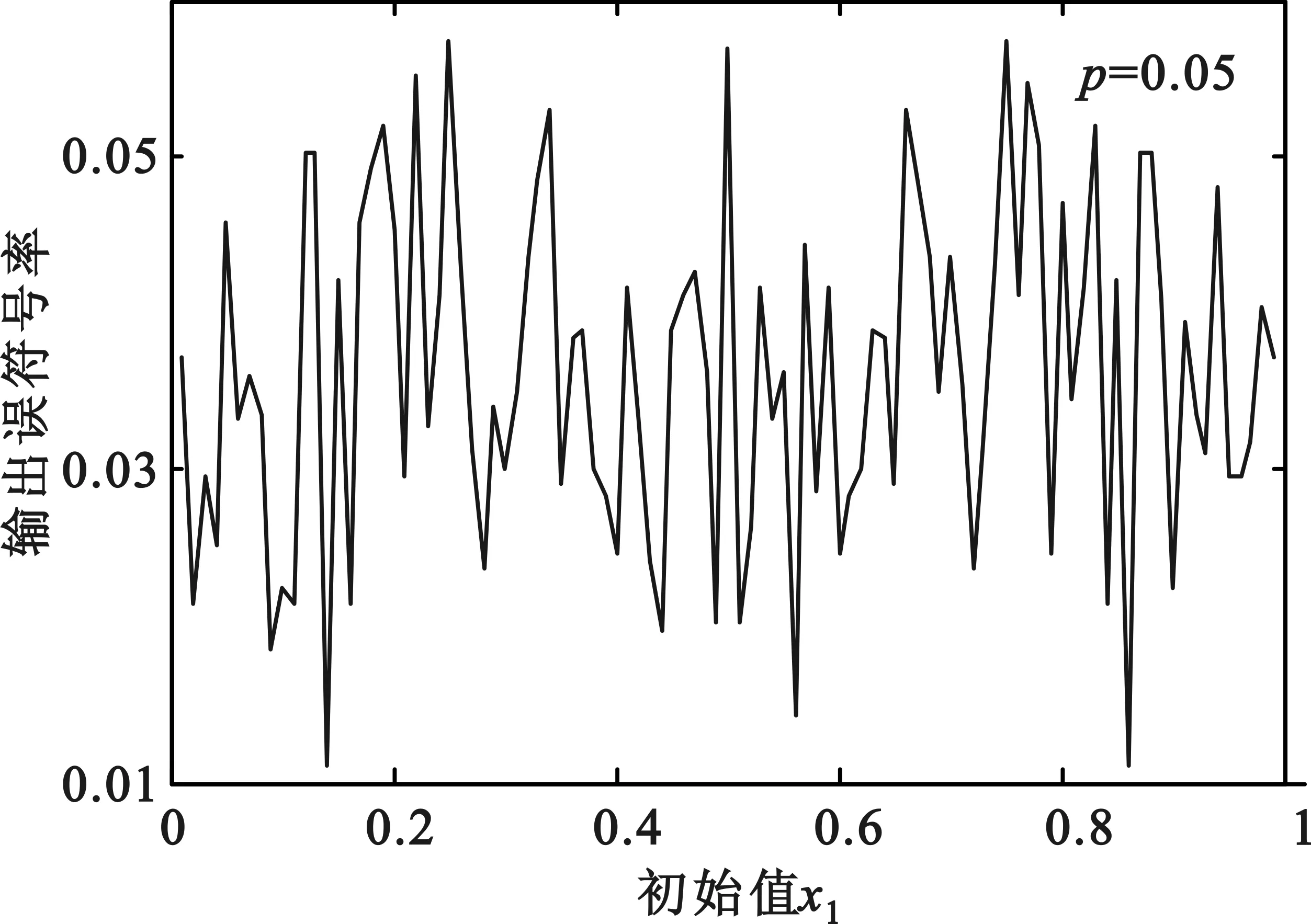
(b)输入误比特率为0.05时的性能分析

(c)输入误比特率为0.07时的性能分析

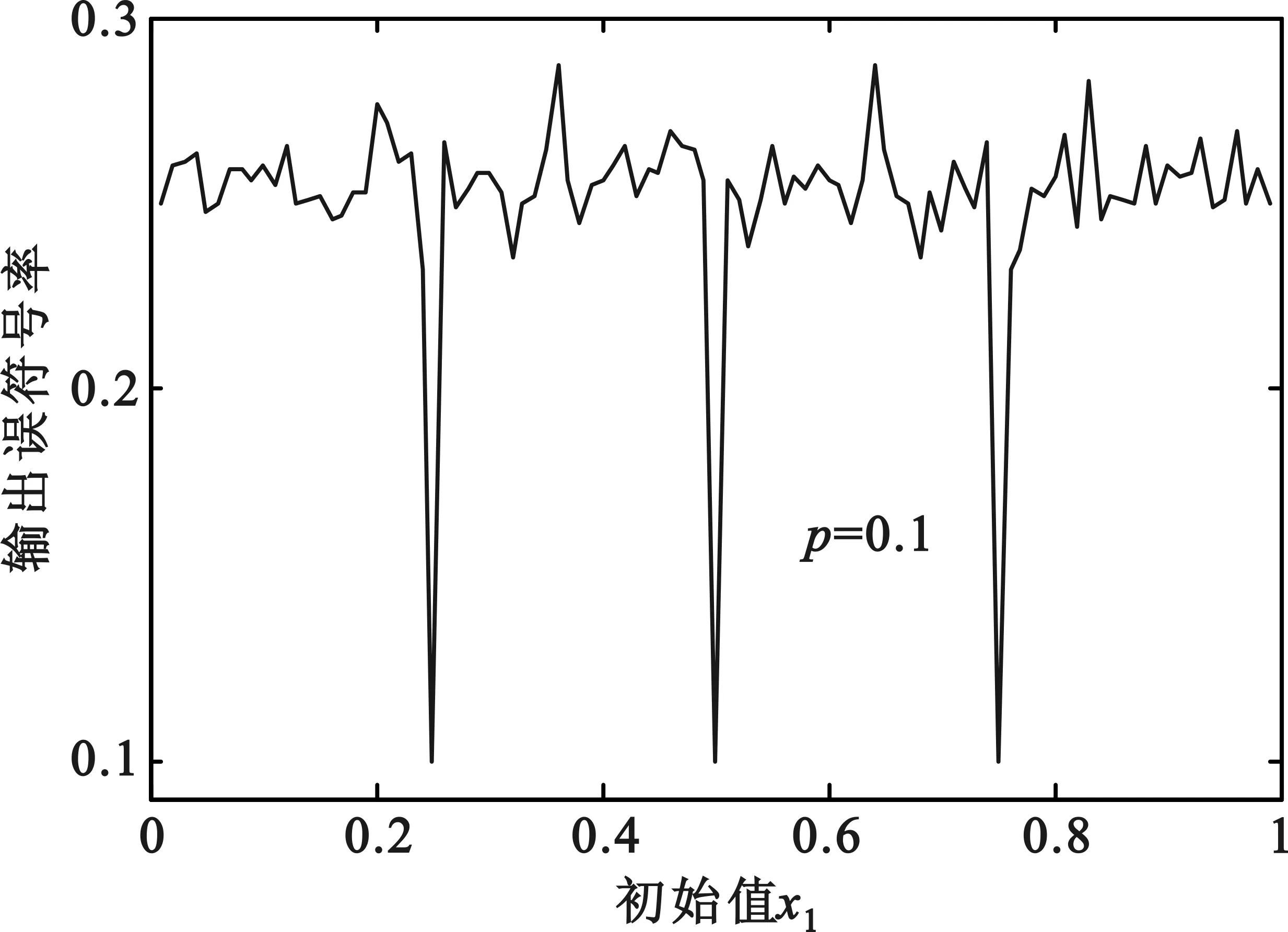
(d)输入误比特率为0.1时的性能分析

当输入误比特率为变量时，RS+卷积级联码对随机错误图样和基于Logistic混沌序列的错误图样的敏感性分析比较如图8所示。

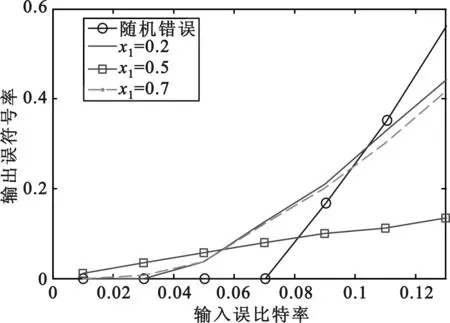
图8 基于Logistic混沌序列的错误图样与随机错误图样的比较

从图8可以看出，当输入误比特率小于0.1时，基于Logistic混沌序列的错误图样对级联码的影响要大于随机错误图样。当x1=0.5时，错误图样为突发错误，在进入RS译码器前产生的错误符号要小于初始值为0.2和0.7所产生错误符号，因此对译码性能影响相对较小。另一方面，初始值为0.2和0.7下的输出误符号率的曲线走向非常相近，又根据图7的分析，说明大部分初始值对RS+卷积级联码译码性能的影响都很接近。

4 结 语

本文提出了一种基于Logistic混村序列的错误图样分布模型，文中以卷积码、RS码以及RS+卷积级联码为研究对象，以随机错误图样为参照，分别研究了泊松分布下三者的译码性能。仿真结果表明，这种错误图样对卷积码和级联码的影响要大于随机错误图样，而RS码对随机错误图样更为敏感。相比于基于随机错误与突发错误结合的模型，本文选取的基于Logistic混沌序列错误图样模型由于具有一定的混沌特性，可以更好地模拟高斯白噪声信道，并且方便产生，具有一定的实际意义，为数字通信的研究提供了一种可行的途径，具有一定的参考价值

[1] 张永光, 楼才义. 信道编码及其识别分析[M]. 北京: 电子工业出版社,2010: 6-8. ZHANG Guang-yi, LOU Cai-yi. Channel Coding and Recognition Analysis[M]. Beijing: Publishing House of Electronics Industry. 2010: 6-8.

[2] 底 强, 苏彦兵, 刘杉坚. 基于改进高斯法的卷积码盲识别方法[J]. 通信技术，2012, 45(10): 68-74. DI Qiang, SU Yan-bing, LIU Shan-jian. Blind Recognition of Convolution Code based onImproved Gauss Algorithm [J]. Communications Technology. 2012, 45(10): 68-74.

[3] Masakawa,Ochiai T. Design of Reed- Solomon Codes for OFDM Systems with Clipping and Filtering[C]// IEEE Conference on Wireless Communications and Networking, WCNC. Kowloon:IEEE. 2007:1361-1366.

[4] Abel A, Schwarz W. Chaos Communications-Principles, Schemes, and System Analysis[J]. Proceedings of the IEEE. 2002,90(5):691-710.

[5] 李辉. 数字混沌通信[M]. 北京: 清华大学出版社,2006: 35-36. LI Hui. Digital Chaotic Communication[M]. Beijing: Publishing House of Qinghua University. 2006: 35-36.

[6] 赵玉新, 王伟, 刘利强. 基于Logistic映射的非线性组合混沌流密码的设计与分析[J].弹箭与制导学报,2007: 370-374. ZHAO Yu-xin, WANG Wei, LIU Li-qiang. A Design and Analysis for Nonlinear Combination Chaotic Stream Cipher based on Logistic Map[J]. Journal of Missiles and Guidance,2007: 370-374.

[7] 邱岳洪, 何晨,诸鸿文. 一种无限折叠混沌映射及其量化序列[J]. 上海交通大学学报, 2002, 36(12):1788-1792. QIU Yue-hong, HE Chen, ZHU Hong-wen. One Chaot icMap with Infinite Collapses and Its Quantified Sequences[J]. Journal of Shanghai Jiaotong University,2002,36(12):1788-1792.

[8] Prasad K, Rajan B S. Convolutional Codes for Network- Error Correction[C]// IEEE Global Telecommunications Conference. Honolulu: IEEE,2009:1-6.

[9] Proakis J G. Digital Communications[M]. Fourth Edition. Beijing: Publishing House of Electronics Industry, 2006: 465-466.

[10] Nyirongo N, Wasim Q Malik, David J Edwards. Concatenated RS-Convolutional Codes for Ultrawideband Multiband-OFDM [C]// IEEE International Conference on Source. Waltham: IEEE, 2006:137-142.

[11] May R M. Simple Mathemaical Model with Very Complicated Dynamics[J]. Nature. 1976(261):281-459.

[12] 姚中华. 水声通信中串行级连纠错编码技术研究[D]. 西安: 西北工业大学. 2006. YAO Zhong-hua. The Research of Serial Concatenated Coding Technology About Underwater Acoustic Communication[D].Xian: Northwestern Polytechnical University. 2006.

Error Pattern’s Influence on Error Correcting Codes based on Logistic Chaotic Sequence

HAO Tian-duo, WANG Ke-ren, JIN Hu, Xiong Zui

(Electronic Engineering Institute, Hefei Anhui 230037, China)

In order to further study the error correcting codes on “bits level”, an error pattern distribution model subject to logistic chaotic sequence is proposed. The error pattern can be generated by mapping the chaotic sequence into binary sequence and controlling the number of "1" in the sequence with a certain method. With convolutional code, RS code and concatenated RS-convolutional code as the research objects and random errors as the references, the decoding performance of these three codes is investigated under the error pattern. Results show that the influence of logistic chaotic sequence-based error pattern on convolutional code and concatenated codes is much greater than that of random error pattern,while RS code is more sensitive to the random error pattern.

logistic chaotic sequence; error pattern; convolutional code; RS code; concatenated code

date:2014-10-29；Revised date：2015-02-20

TN911.22

A

1002-0802(2015)04-0397-07

郝天铎(1989—)，男，硕士研究生，主要研究方向为数字通信；

王可人(1957—)，男，教授，主要研究方向为主要无线通信、信号处理；

金 虎(1973—)，男，副教授，主要研究方向为主要无线通信、信号处理；

熊 最(1988—)，男，博士研究生，主要研究方向为数字通信、通信信号处理。

10.3969/j.issn.1002-0802.2015.04.005

2014-10-29；

2015-02-20