一个大范围混沌系统及其在DCSK 中的应用

鲜永菊，谢东明，付明明，黎金龙

（1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 光电工程学院，重庆 400065）

0 引言

调制过程是现代通信系统中的核心部分。通信中的调制主要作用是对信号进行处理，使信号符合传输的需求。而随着以往的调制方案研究的逐渐完善，研究人员对调制方案有了新的性能需求。调制的过程中使信号产生出类噪声的性质达到保密通信的目的。在文献[1-3]中提出了新的混沌系统，同时构建了分数阶混沌系统、多翼混沌系统、超混沌系统、多渦卷混沌系统及恒定李雅普诺夫指数（Lyapunov exponent，LE）系统等。而混沌是类无规则、类随机的动力学行为，将其引入到调制中可以达到保密通信的效果。由此，DCSK 被提出和进行更深入的研究。

在DCSK 方案的改进上，文献[9]研究了具有M 进制的多级码移差分混沌移位键控。文献[10]对脉冲位置调制与DCSK 进行了研究。文献[11]对于脉冲位置调制与DCSK 结合的进一步优化有相关研究。研究人员对差分混沌键控的载波索引调制和广义载波索引差分混沌键控调制进行了研究。文献[14]提出了具有码索引调制的差分混沌移位键控方案。文献[15]研究了M 进制以及码索引调制结合的差分混沌移位键控方案。文献[16]提出了具有码索引的多载波M 进制差分混沌移位键控系统。在DCSK 中应用混沌系统，文献[17]研究了一类具有无限平衡的新型混沌流。文献[18]采用重复扩频序列在多载波差分混沌移位键控系统中进行研究。文献[19]采用双曲正弦混沌系统进行相关研究。以上研究旨在对DCSK 优化，提升误比特率性能。

由于实际情况中受温度、湿度影响，混沌系统的参数可能会产生小范围的波动。而混沌对参数变化极其敏感，参数细微的变化会导致混沌特性的消失并表现出周期性，这样就不能保证DCSK 的保密性能。文献[20]提出了一个在参数区间[10，1000]内保持混沌特性的混沌系统。文献[21]提出了参数区间在[0，2 000]内保持混沌特性的混沌系统。这一类混沌系统具有当参数变化波动情况下仍能够保持混沌特性的特点。

在DCSK 中采用不同的混沌系统时，最终得到的误比特率性能也不同。本文旨在研究DCSK 中具有更好的误比特率性能的混沌系统，同时考虑参数不稳定变化时，使其可以在DCSK 中能提供稳定的混沌信号。本文研究了一个大范围混沌系统的混沌特性，之后在DCSK方案下进行蒙特卡洛仿真分析。研究发现该大范围混沌系统能保证误比特率性能稳定，对比已有研究误比特率性能更优。

1 混沌系统模型

本文提出公式（1）的混沌系统模型：

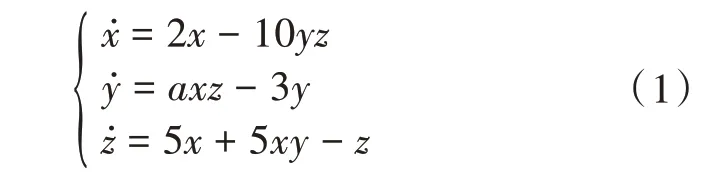
式中，，是微分方程的变量；是可变化的参数。

在该系统中，参数=1 的情况下，系统能够保持混沌特性。图1 是混沌系统在参数=1，初始状态[0.05，0.05，0.05]的情况下的相图。图中，系统具有共存混沌吸引子。在此时的参数以及初始状态条件下，计算得到的李雅普诺夫指数分别为0.592 5，0.080 1，-2.672 5，系统处于混沌状态。

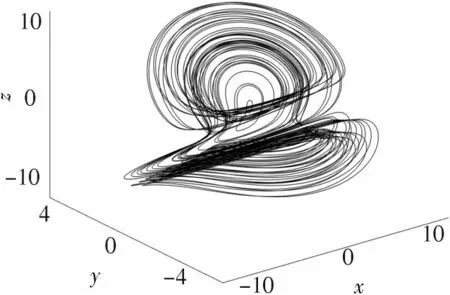
图1 x-y-z的相图

2 混沌系统分析

令式（1）中的左边等于0，得到：

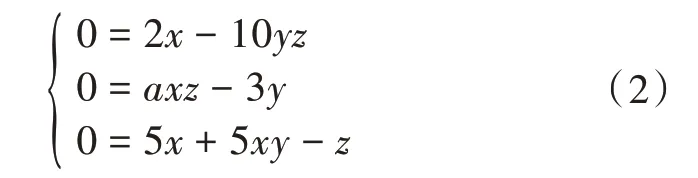
由式（2）可以得到雅可比矩阵：

当=1 时，式（2）共 有5 个平衡点：=(0，0，0)，=(-1.07，-0.28，0.78)=(-2.80，-0.72，0.78)=(1.07，-0.28，-0.78)，=(-2.80，-0.72，0.78)。

由平衡点可以得此平衡点的特征根为：

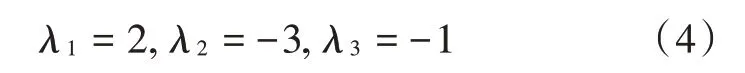
由平衡点可以得此平衡点的特征根为：

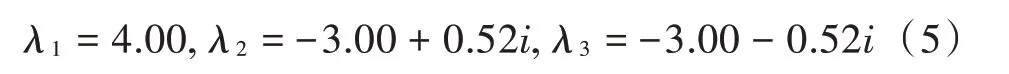
由平衡点可以得此平衡点的特征根为：

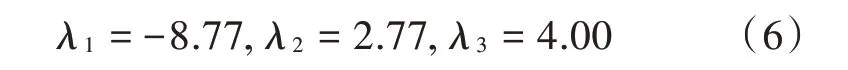
这5 个平衡点都是不稳定的鞍焦点。

式（1）混沌系统同时具有在超大参数范围内保持混沌特性的特点。图2 中展示了当参数在[1，10]的范围内的李雅普诺夫指数（LE），可以看出李雅普诺夫指数有正数，呈现出混沌特性。图3 是参数[1，10]范围内的分岔图。同时，混沌系统在参数更大的范围时，系统均保持混沌系统特性，[1001，10 000]参数范围内的李雅普诺夫指数如图4 所示。

图2 [1，10]范围内的LE

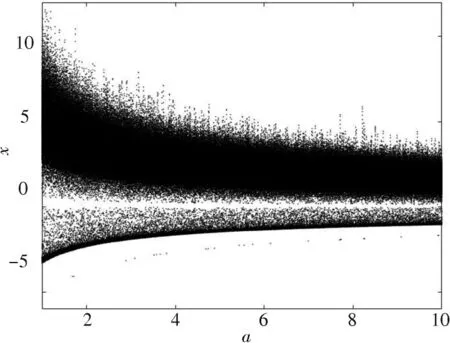
图3 [1，10]范围内x 的分岔图

图4 [1001，10 000]范围内的LE

3 DCSK 系统模型

DCSK 是混沌系统在通信系统的有效应用方案，调制中应用混沌系统可以提供保密通信能力。

图5 是本文研究DCSK 中性能的发送端的模型。混沌信号产生后通过时延在两个时隙中传输，在第一个时隙中作为参考信号用以在接收端中实现非相干解调；在第二个时隙中与信息承载信号进行调制作为传输信号。

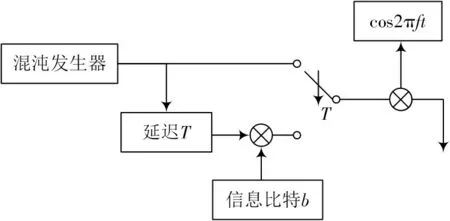
图5 DCSK 发送端模型

图6 为接收端模型。接收端接收到传输的信号后，先通过频谱搬移将在发送端搬移到高频的信号恢复；然后将恢复得到的信号通过低通滤波器，消除信道中的噪声和其他多余的高频干扰信号。通过时延将第一个时隙中的混沌参考信号延迟一个时隙用以对第二个时隙中的传输信号进行解调。最后通过阈值判决输出信号，得到发送端的信息。

图6 DCSK 接收端模型

4 混沌系统在DCSK 的性能分析

4.1 参数稳定的误比特率

本节研究当混沌系统参数稳定情况下的误比特率性能。图7 为本文混沌系统与文献[19]中简单双曲正弦混沌系统的对比分析。

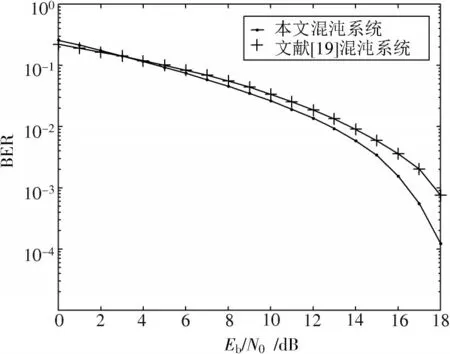
图7 参数稳定的误比特率

当参数=1，在初始状态[0.05，0.05，0.05]的情况下进行模拟仿真，系统仿真得到的误比特率性能如图8中所示。在信噪比处于0～5 dB，本文系统与文献[19]的误比特率性能没有太大的区别；在信噪比大于5 dB 时，随着信噪比的增大，本文混沌系统的误比特率性能提升大于文献[19]。可以得到结论：参数稳定情况下，本文混沌系统误比特率性能更优。本文混沌在不同参数取值情况下仍然能保持混沌性质。对本文在初始状态值不变的情况下混沌系统取参数=2 或10 进行仿真，结果如图8 所示。

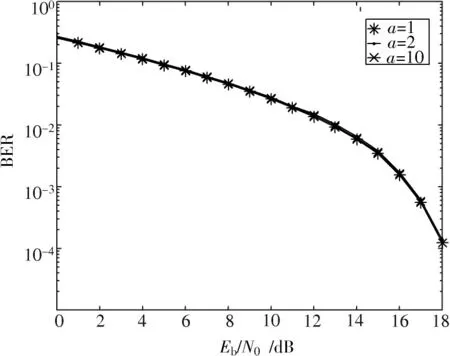
图8 参数稳定的误比特率

4.2 参数不稳定的误比特率

混沌系统对参数具有敏感性，而当实际中实现混沌系统时，元器件大多都具有不同程度的热敏感特性，所以混沌系统可能会表现出混沌参数不稳定的情况，对DCSK 造成影响。因此，在本节中考虑了混沌系统参数不稳定情况下在DCSK 中的误比特率性能表现。

由于混沌系统对参数的敏感性，参数发生变化时，混沌系统可能会失去混沌特性进而无法保证保密通信。为了验证大范围混沌的优点，本文进行了参数不稳定波动情况下的仿真。图9a）是模拟仿真中发送的信息信号波形；图9b）是模拟仿真当式（1）中参数在区间[3，4]内不稳定波动时，信息信号与混沌系统产生的混沌信号调制后的信号波形；图9c）是模拟仿真参数范围小的混沌系统当其参数在不稳定波动时，信息信号与混沌系统产生的混沌信号调制后的信号波形。

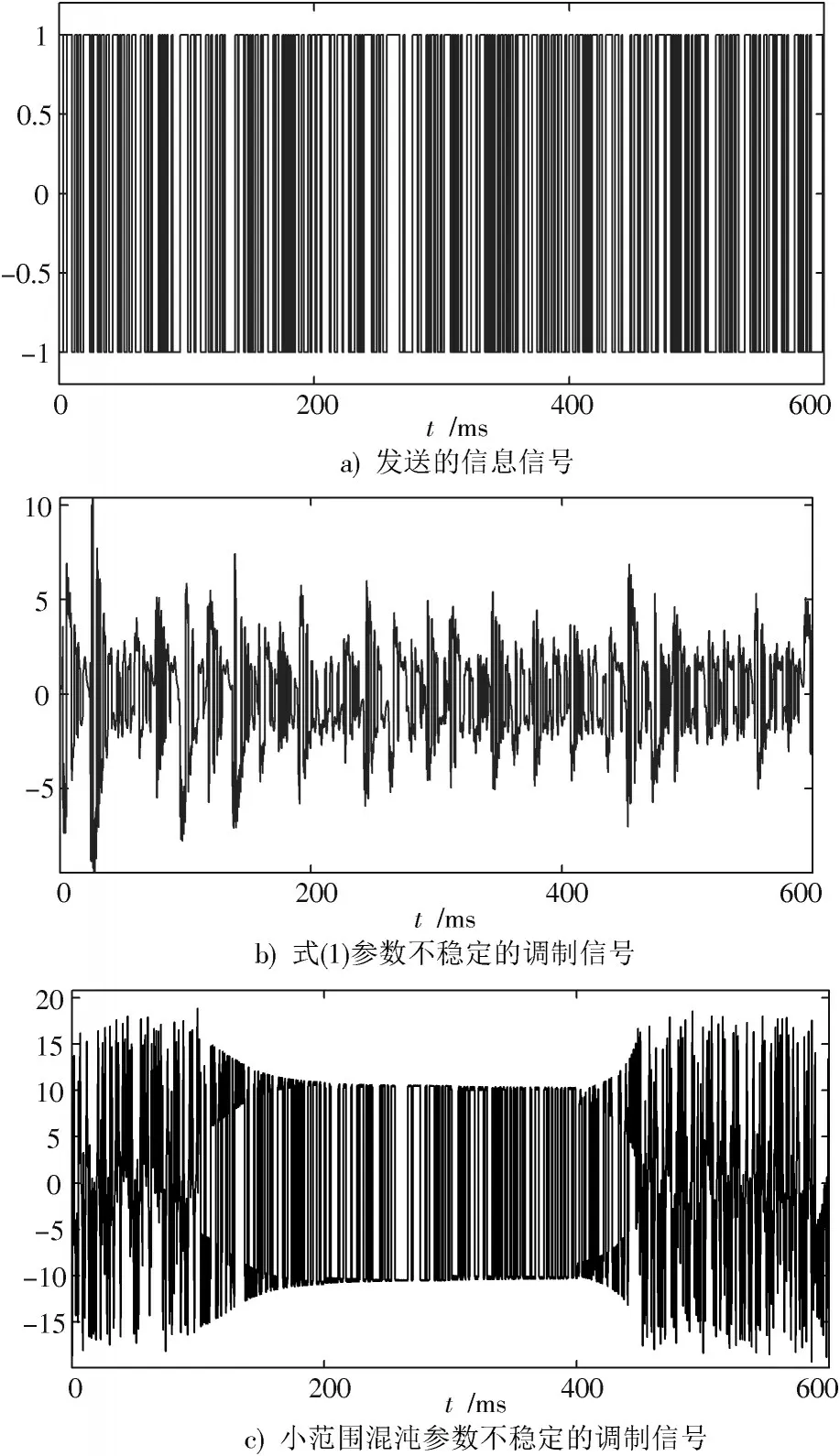
图9 信号波形对比

通过图9b）和图9c）的对比可以发现，大范围的混沌系统在参数不稳定的情况下，系统由于本身特性即使参数波动也能保持混沌特性，所以调制后的信号有保密通信的能力。相对地，小范围内的混沌调制信号由于参数的波动，混沌系统本身可能会失去混沌特性，变为周期或常数，如图9c）后半段部分出现于原信息信号相同或相反，这样将失去保密性能。

验证了大范围混沌系统在参数不稳定情况下仍然能稳定保证保密性能的特性后，本文对当参数不稳定时的系统误比特率进行仿真。图10 是在参数波动下，本文混沌系统与文献[21]中大范围混沌系统的误比特率性能的对比分析。

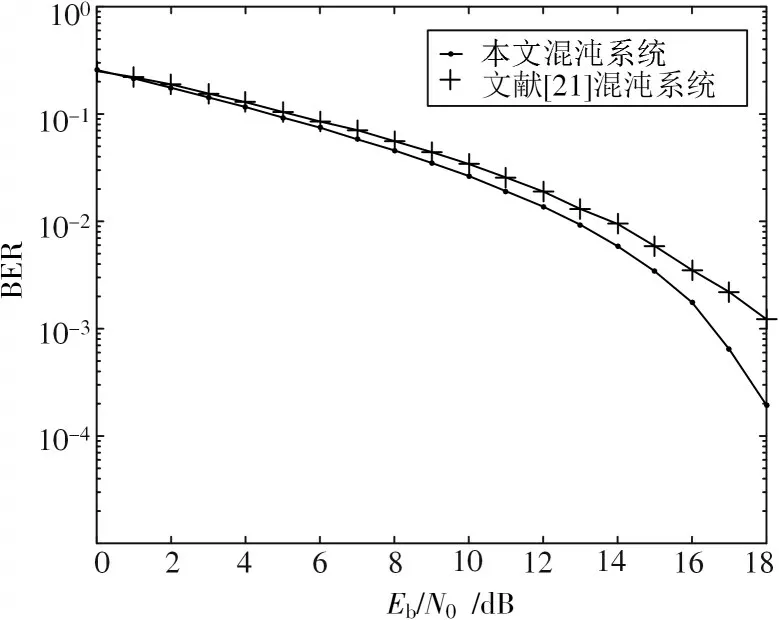
图10 参数不稳定的误比特率

通过仿真结果可以发现：本文的混沌系统在参数波动的情况下，信噪比处于0～5 dB，本文系统与文献[21]的误比特率性能相差没有太大的区别；当信噪比大于5 dB时，随着信噪比的增大，本文研究混沌系统的误比特率性能更优。图11 展示了参数稳定=1 和参数不稳定在区间[3，4]内波动的误比特率对比。

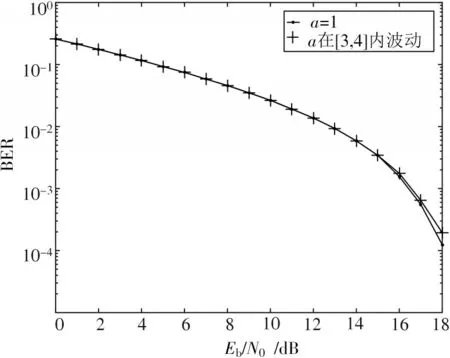
图11 参数稳定和不稳定的误比特率对比

由图11 中参数稳定与不稳定的误比特率对比可以发现，当参数波动时误比特率性能有细微变化，但与参数稳定对比差距不大。参数在更大区间范围波动时误比特率性能符合图11，说明本文混沌系统在参数不稳定波动时系统能保持稳定的误比特率性能。

5 结语

本文研究具有大范围特点的混沌系统在DCSK 中应用的误比特率性能。首先对大范围的混沌系统进行了混沌特性的验证。对大范围混沌在DCSK 中的误比特率性能进行仿真，发现参数稳定情况下误比特率性能优于同类文献研究。而当参数不稳定情况下，对比参数范围小的混沌系统能保证DCSK 的保密性能，同时误比特率性能稳定且更优。研究解决了误比特率性能需要提升和参数不稳定下不能保证混沌信号的问题。在电路结构不变的情况下，如果能对参数进行调控，则可为系统提供多样性，未来也可研究多参数波动混沌系统在DCSK 中的误比特率性能。