基于滑模变结构模型参考自适应的电气无级变速器无传感器控制

朱 瑛 程 明 花 为 张邦富 王 伟

（东南大学电气工程学院 南京 210096）

1 引言

近年来，电气无级变速器（Electrical Variable Transmission，EVT）电机因可实现无级变速，有潜力代替传统机械齿轮箱等特点而成为电机学科的一个研究热点[1,2]。EVT既可用于混合动力汽车等领域[3,4]，也可用于风力发电，构成所谓的双功率流风力发电系统（Dual Power Flow Wind Energy Conversion System，DPF-WECS）[5-7]。在该 DPF-WECS系统中，风力机与EVT电机的外转子连接，内转子与普通同步发电机相连，由同步发电机发电直接并网。此系统去除了传统风力发电系统中最薄弱的齿轮箱环节，且同时提供机械功率流和电功率流，可优化功率配置。电池储能系统的应用可使系统根据电网需求调节输向电网功率，以使整个风力发电系统成为稳定的功率输出源。此外，由于该系统直接由同步发电机输出电能至电网，不经过电力电子变换器，因此电能谐波小，质量高。永磁电机具有功率密度大，效率高等优点，因此永磁EVT电机（PM-EVT）将是本文的研究对象。

矢量控制是永磁同步电机（PMSM）最常用的控制方法，而高性能的PMSM矢量控制需要精确的转速及转子位置信息。常用的机械式传感器如光电编码器、旋转变压器等可用来检测转速及位置，但是传感器的安装使系统成本增加，运行可靠性降低，且受工作环境等影响。特别是本文所述双功率流风力发电系统需要通过内转子驱动同步发电机发电，为保证输出电压、频率恒定，内转子转速需保持恒定且波动小，即需实现内转子转速的精确控制。而内转子控制所需的转子位置信息不仅仅与内转子有关，还受外转子的影响，需通过内外转子位置差得到，若通过传统机械传感器测量位置，由于传感器本身存在一定的误差，两个传感器作差值计算更会导致误差积累，从而影响内转子控制精度，甚至使控制失败。因此，本文对内转子采用无位置传感器控制。

目前，基于PMSM的无位置传感器方法主要有基于反电势估算法[8,9]、高频信号注入法[10]、扩展卡尔曼滤波器法[11]、滑模观测器（SM）法及模型参考自适应（MRAS）法[12-15]等。其中MRAS法具有结构简单，运算量低等优点，成为一种常用的无传感器控制方法。传统MRAS方法通过PI控制器产生估计转速，但是PI控制器参数调节较困难，且定参数的PI控制器随着电机参数及工作情况的改变就难以达到最佳性能。为此，本文在传统MRAS控制方法的基础上提出了一种将SM与MRAS结合的转速观测器，用SM算法替代了传统MRAS中的PI控制器。传统基于PMSM的MRAS方法都以电流模型为可调模型[15]，而这过程中需对电流模型进行一定的变换，本文提出了磁链模型为可调模型的方法，简化了变换过程，并与以电流模型为可调模型时进行比较。且考虑传统常值切换的SM算法中抖振的存在，本文采用分段切换法来改善这一现象，并应用于SM-MRAS控制方法中。最后通过搭建双功率流风力发电系统实验平台，对所提SM-MRAS控制策略进行了实验验证。

2 DPF-WECS工作原理与数学模型

2.1 DPF-WECS工作原理

双功率流风力发电系统（DPF-WECS）结构框图如图1所示。虚线框中的PM-EVT电机由绕线式定子（#1）、永磁外转子（#2）及绕线式内转子（#3）组成，其中外转子位于定子与内转子之间。外转子与风力机相连，内转子与同步发电机相连，定子绕组与内转子绕组间通过背靠背变换器相连，直流母线通过DC-DC变换器与电池储能装置相连。如图1所示，由风力机传递过来的机械功率Pm1经过EVT电机时可分为两路：①机械功率流Pd，即以机械功率的形式，通过电磁场耦合在内外转子间传递；②电功率流Pes，即通过外转子与定子耦合，由定子绕组、背靠背变换器、内转子绕组和集电环传递。

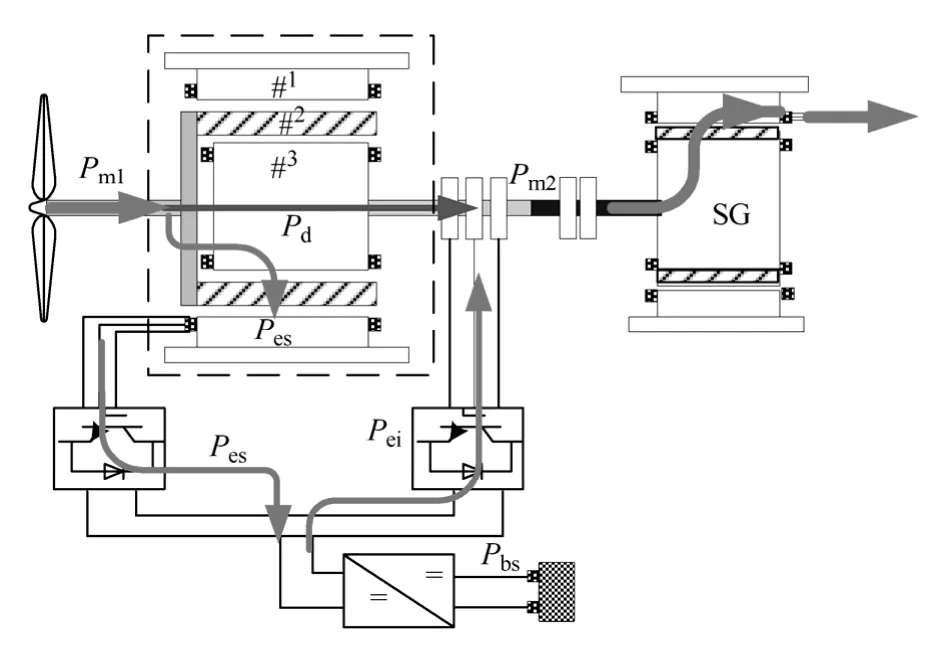
图1 双功率流风力发电系统结构框图Fig.1 Configuration of DPF-WECS

风力机输入功率Pm1为

式中 Tm1——外转子转矩；

ωo——外转子转速。

内转子输出功率Pm2为

式中 Tm2——内转子输出转矩；

ωi——内转子转速。

外转子通过外气隙电磁耦合，由定子绕组输出的电磁功率Pes为外转子通过内气隙电磁耦合传给内转子的机械功率为

上式中 Tf1——定子与外转子间的外气隙转矩；

Tf2——外转子和内转子的内气隙转矩，因此有 Tm1=Tf1+Tf2。

2.2 PM-EVT数学模型

经过诸多文献研究证明，外转子内外永磁体的耦合可忽略不计[7]，则PM-EVT电压及磁链方程为

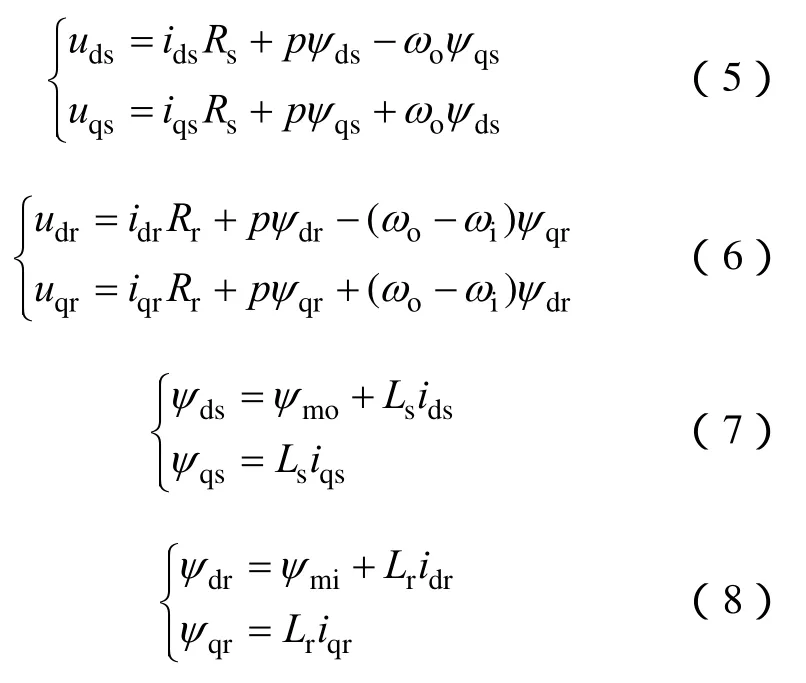
式中 Rs,Rr——定子绕组和内转子绕组的电阻；

Ls,Lr——定子绕组和内转子绕组的电感；

ωo,ωi——外转子和内转子转速；

uds,uqs,udr,uqr——dq坐标系下定子绕组和内转子绕组的电压；

ids,iqs,idr,iqr——dq坐标系下定子绕组和内转子绕组的电流；

ψds,ψqs,ψdr,ψqr——dq 坐标系下定子绕组和内转子绕组的磁链；

ψmo,ψmi——定子绕组和内转子绕组匝链的永磁磁链；

p——微分算子。

PM-EVT电机定子绕组，外转子和内转子转矩分别为

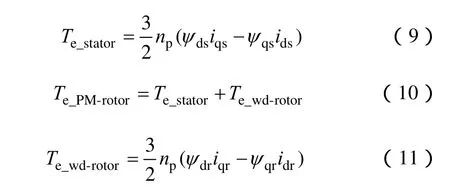
式中 np——PM-EVT电机的极对数。

PM-EVT电机可看作是一台永磁外电机及一台永磁内电机的组合。永磁外电机由定子及外转子组成，永磁内电机则由外转子及内转子组成。永磁外电机的转速ω1即为外转子的转速ωo，而永磁内电机的转速ω2为内外转子转速差ωo-ωi。永磁外电机转矩即为定子绕组转矩Te_stator，永磁内电机电磁转矩则对应于内转子绕组转矩Te_wd-rotor。

3 SM-MRAS无传感器控制

3.1 基于电流可调模型的MRAS

对PM-EVT电机数学模型进行变换，将式（8）代入式（6）中，并改写成电流模型的格式得

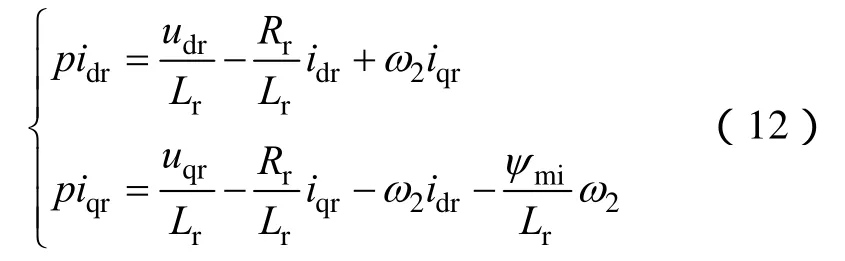
将式（12）改写成矩阵形式得

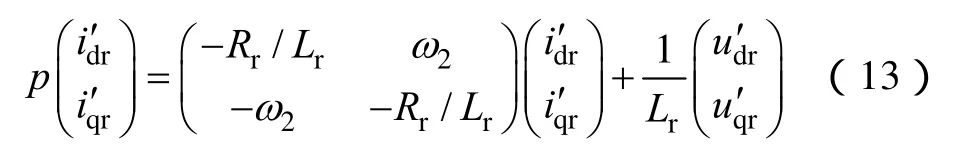
其中

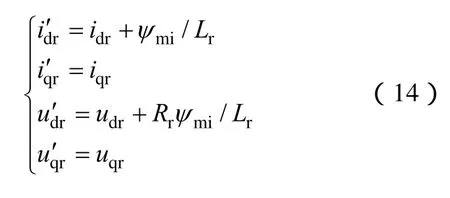
将（13）中的电流、转速替换为估计值，此时可得MRAS算法基于电流的可调模型为

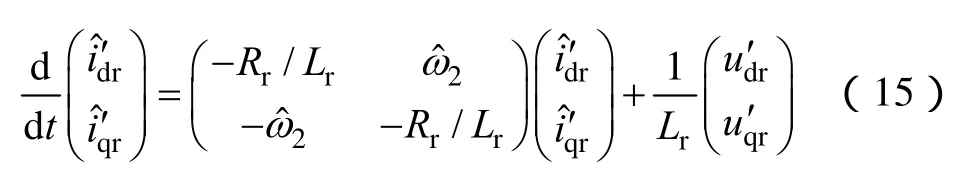
式中，^表示变量的估计值。

则根据Popov超稳定理论，传统基于电流为可调模型的MRAS控制策略的估计转速为

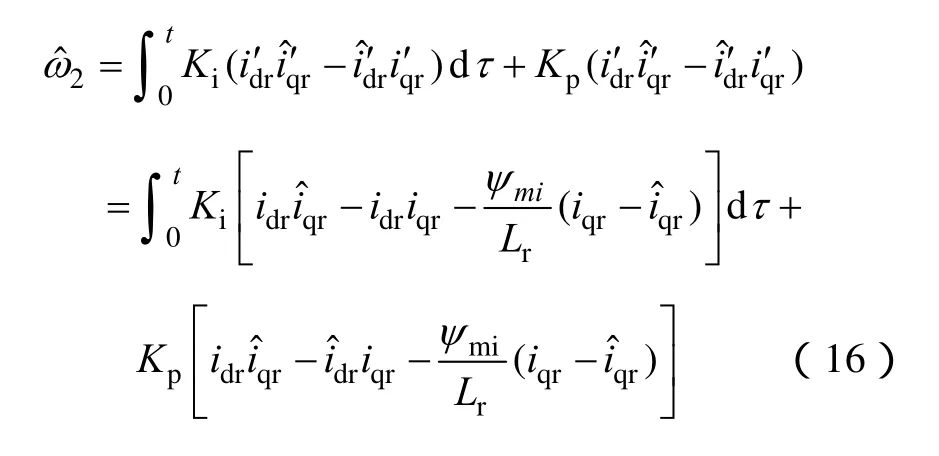
式中，Kp为比例参数；Ki为积分参数。

根据式（16），即可估算出永磁内电机的转速，再对转速进行积分，即可得到转子位置角。

3.2 基于磁链可调模型的MRAS

由上述推导可知，以电流为可调模型时，需对电流进行一定的变换，如式（14）所示，才能实现MRAS控制算法。

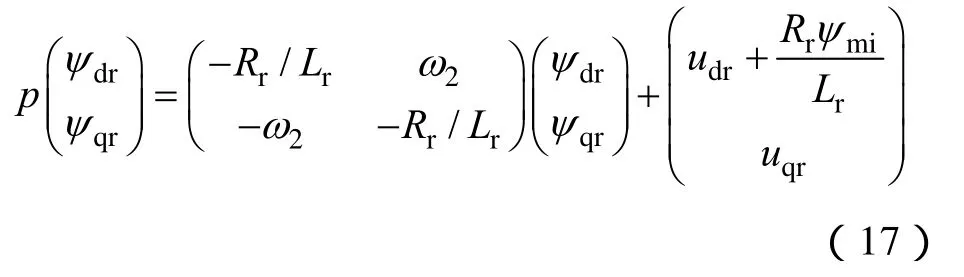
对式（6）进行变换，可得永磁内电机磁链格式的数学模型为将式（17）中的磁链、转速替换为估计值，此时可得MRAS算法基于磁链的可调模型为

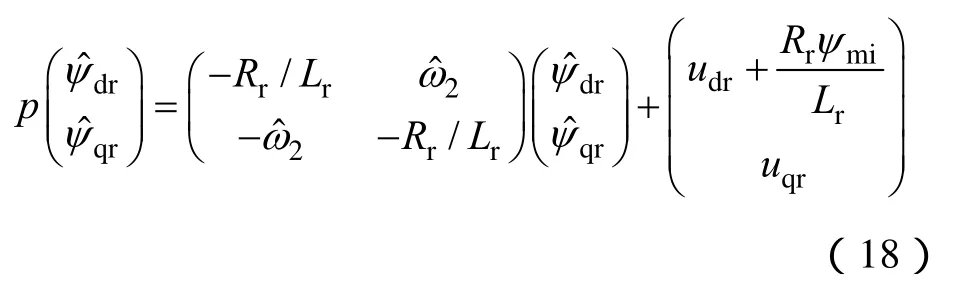
与上述电流为可调模型的MRAS控制策略类似，可得到以磁链为可调模型的MRAS控制估计转速为

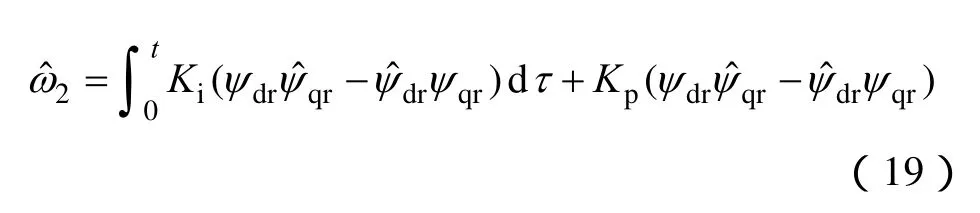
综上所述，基于电流模型和磁链模型的MRAS控制框图如图2所示，两种控制方法原理一致，但以磁链为可调模型时算法更简单，两种方法的具体性能将通过实验结果验证。

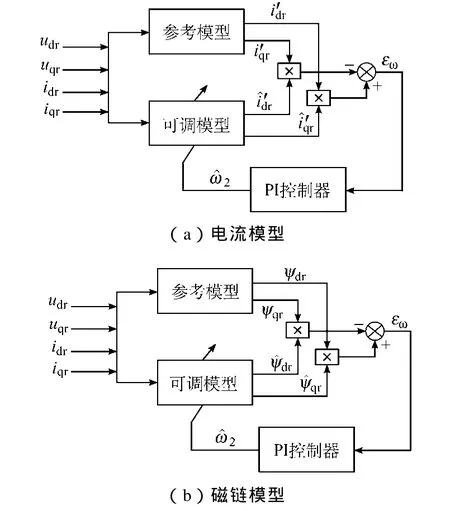
图2 MRAS控制框图Fig.2 Control configurations of the MRAS

3.3 基于磁链可调模型的SM-MRAS

由于传统MRAS控制策略的速度观测以参考模型为基础，受电机自身参数影响很大，电机参数的准确度将直接影响转速辨识的精度。且MRAS采用PI控制器调节得到估计转速，PI参数较难调节，当转速或电机参数变化时，定参数的PI控制器难以达到最佳性能。而滑模观测器采用估计偏差来确定滑模控制机构，使控制系统的状态最终稳定在设定好的滑模超平面上，对参数依赖性较小。

因此本文提出了将滑模变结构与模型参考自适应结合的SM-MRAS转速观测器，采用滑模变结构方法替代上述传统MRAS控制中的PI控制器环节，使转速观测器更简单，更稳定。而基于3.1节、3.2节分析可知，磁链为可调模型时MRAS控制更简单，因此SM-MRAS控制策略的分析也以磁链为可调模型。

滑模变结构算法选择切换面的原则是：当系统发生滑动时s(e)=0，滑动运动是渐进稳定的，并且具有较好的动态品质[12]。按照这一原则，本文构造滑模变结构MRAS转速辨识器的切换函数形式如下

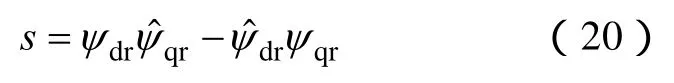
对切换函数s求导，可得

将式（17）、式（18）代入式（21）可得

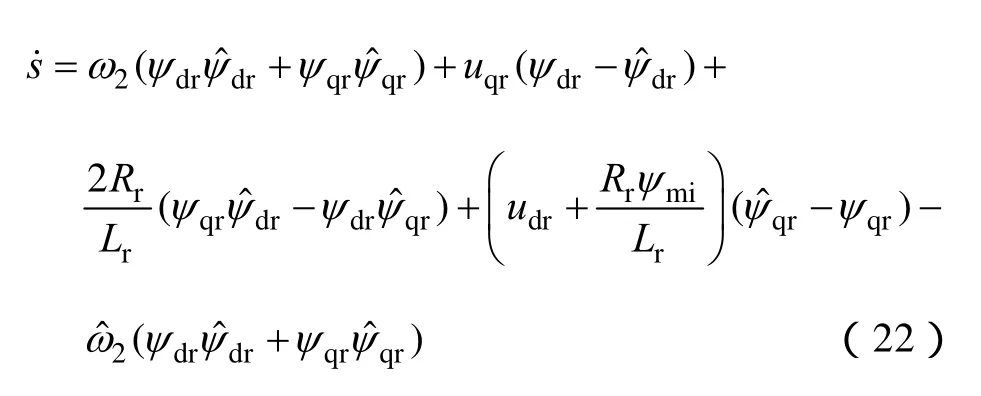
当采用常值切换控制法时，滑模变结构转速估算表达式如下：

式中，M为一个大于零的常数；sign()为符号函数。

将式（23）代入（22）中，可得

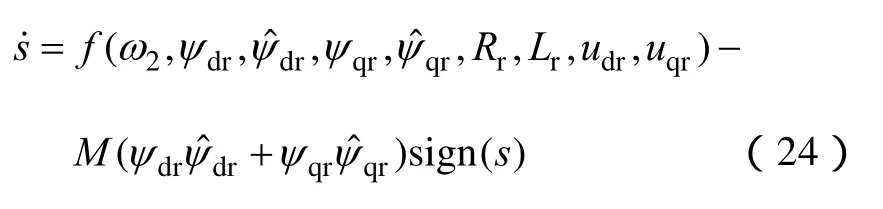
式中，f()是参考磁链ψdr、ψqr，估计磁链ψˆdr、ψˆqr，电压 udr、uqr，电感Lr，电阻Rr和转子电角速度ω2的函数。

根据滑模变结构控制基本思想，如果系统进入滑动模态控制，即s˙=0，则根据式（22），可得电机等效角速度表达式为

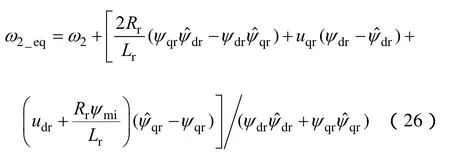
从式（26）中可看出，当电机估计磁链与实际磁链相等时，等式第二项及第三项为0，则等效角速度即为实际角速度。根据式（23），估计的电机电角速度是切换函数的离散函数，其低频分量即为等效速度。因此，当高频开关分量反馈给观测器后，低频分量就可以通过低通滤波器获得，即为电机估计电角速度，控制框图如图3所示。

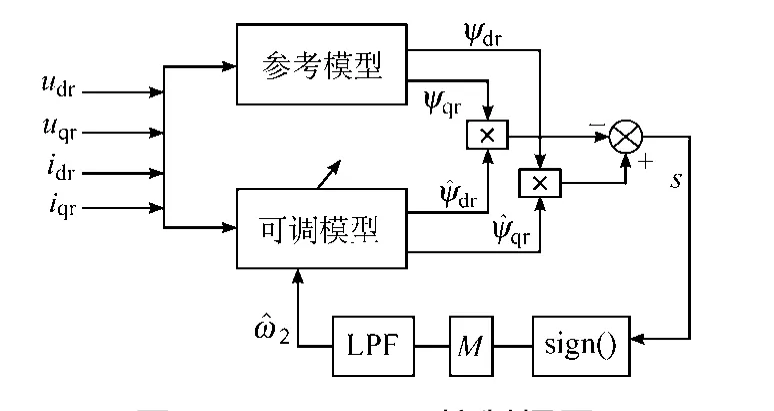
图3 SM-MRAS控制框图Fig.3 Control configuration of the SM-MRAS

在传统的滑模变结构算法中，由于系统采样频率受限，且受切换开关惯性等影响，滑动模态并不是理想的光滑运动，而是呈现了上下的抖动运动，即产生抖振现象[16]。虽然经过了低通滤波器滤波，一定程度改善了抖振，但并不能完全消除。而且低通滤波器的加入会使信号产生相位滞后。因此，本文采用了改进的滑模控制转速估算切换方法，使估算转速函数成为饱和函数，消除抖动现象。

改进的估算转速函数如下[17]：

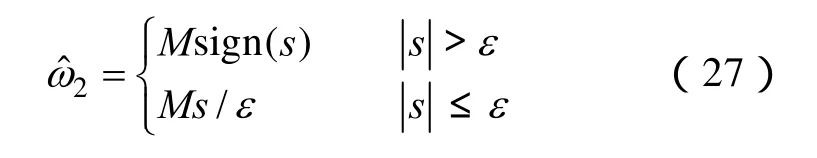
式中，ε是设定的边界常数，可选取一个很小的正数，ε的选择也会影响转速估算精度，可根据实际情况调节ε的大小。

由于采用原符号函数转速估算时，需采用低通滤波器改善抖振现象，而采用饱和函数转速估算切换的方法，通过合理选择边界常数的值，无需低通滤波器便可消除抖振，解决了信号相位滞后问题，并提高转速估计速度。而PM-EVT内转子的给定转速随着外转子转速的实时变化而变化，因此内转子转速的控制速度需较快，文中采用的饱和函数转速估算切换SM-MRAS更适合内转子的控制。

3.4 内转子无传感器控制

EVT电机的内转子与同步发电机相连，内转子传递机械功率给同步发电机，通过同步发电机发出电能并网。同步发电机要并入电网必须满足输出电压频率与电网电压频率相同，即同步发电机需维持同步速旋转，因此需控制内转子转速为恒定同步速。

内转子无传感器控制框图如图4所示。转速环的给定转速为同步发电机同步速与外转子转速之差，实际转速是通过上述SM-MRAS估测所得。转速环PI的结果作为电流环的给定，采用空间矢量脉宽调制（SVPWM）矢量控制，通过改变内转子绕组的通电频率使内转子保持转速恒定。

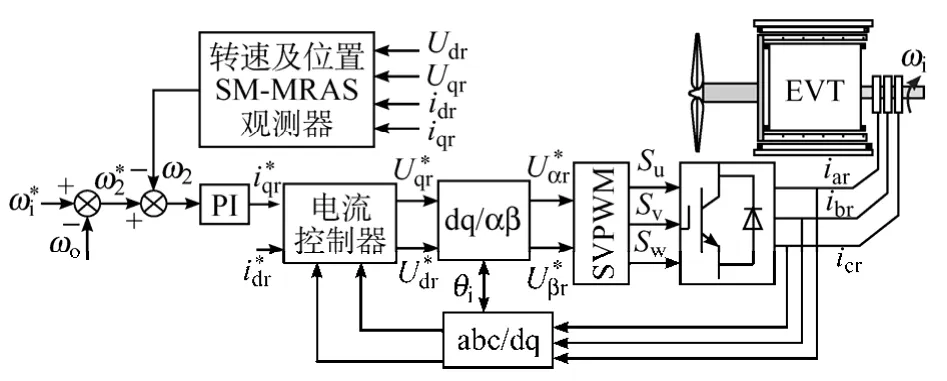
图4 内转子无传感器控制框图Fig.4 Configuration of the sensorless control for the inner rotor

4 实验研究

为了验证文中所提出的针对PM-EVT内转子的改进型SM-MRAS无传感器控制策略的有效性，搭建了实验平台。实验样机如图5a所示，可分为风力机模拟、PM-EVT电机及发电机三部分。风力机由异步电机及减速齿轮箱模拟，发电机由永磁同步电机模拟。PM-EVT内转子及异步电机均采用矢量控制，控制平台基于dSPACE1103，将已在Matlab/Simulink得到验证的控制模型导入，实现对控制策略的验证，控制平台如图5b所示。

图5 实验平台Fig.5 Experimental platform

为测试本文提出的改进型SM-MRAS策略的性能，将其与传统的MRAS及未改进的SM-MRAS策略比较。首先，风力机及外转子保持静止，只控制PM-EVT内转子，且不加载，内转子转速从240r/min突变至300r/min，然后再减速至240r/min。基于电流可调模型及磁链可调模型的MRAS无传感控制策略下的内转子实验波形分别如图6、图7所示。图6a及图7a展示了内转子估计转速、实际转速及绕组A相电流波形，图6b及图7b展示了内转子估计位置与实际位置。由实验结果可见，基于电流模型和磁链模型的两种MRAS策略下内转子转速均能较好的实现转速闭环控制，且估计转速与实际转速吻合度高，误差小，空载电流波形也较正弦，即均可实现内转子无传感器控制。但实验时需耗费较长时间来选择合理的PI参数，且当电机工况发生变化时定参数PI将难以达到最佳控制效果。

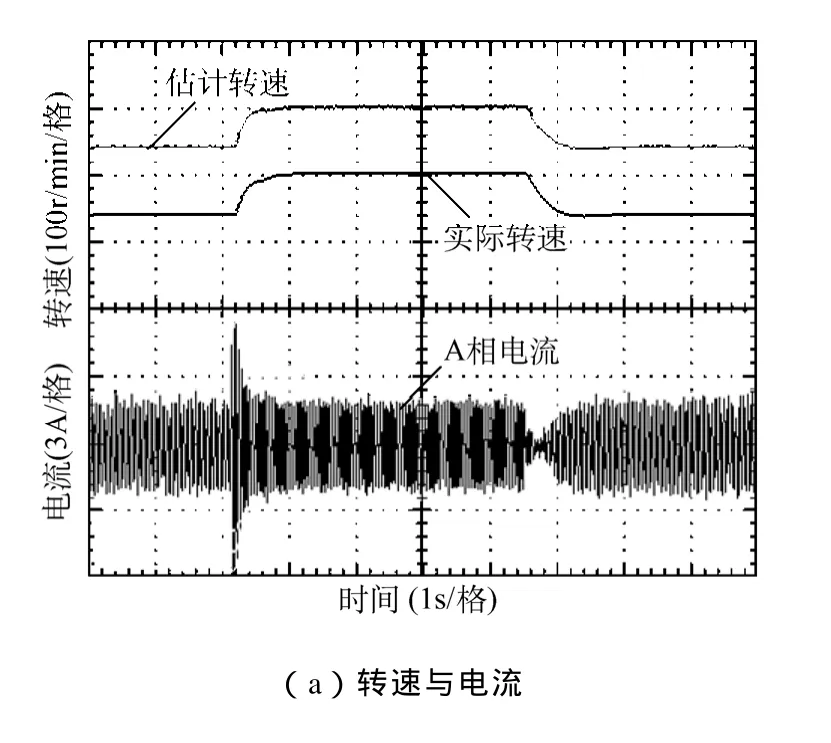
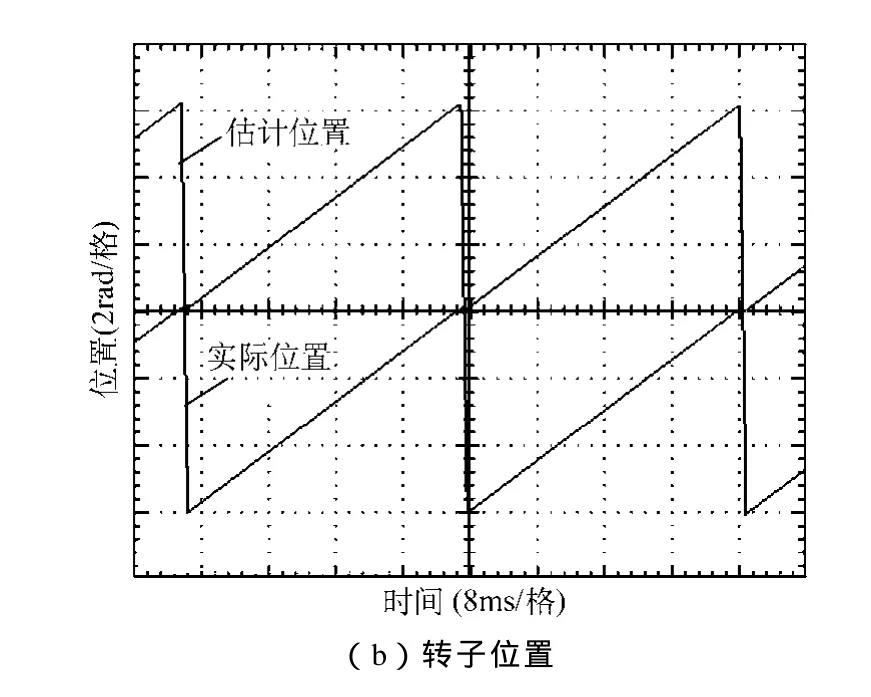
图6 基于电流可调模型的MRAS实验波形Fig.6 Experimental waveforms of MRAS with the current adjustable model

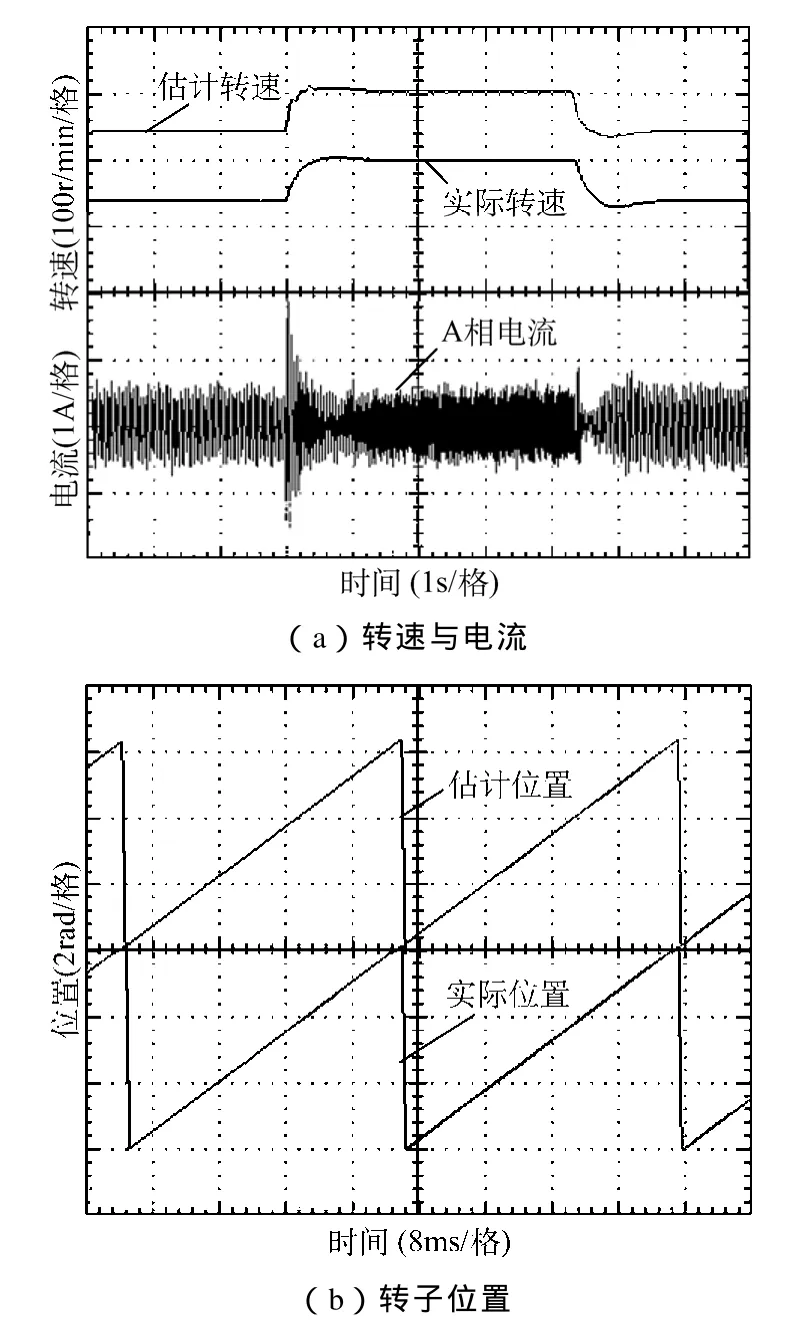
图7 基于磁链可调模型的MRAS实验波形Fig.7 Experimental waveforms of MRAS with the flux linkage adjustable model

由上述分析可知基于磁链模型的MRAS算法更为简单，因此在SM-MRAS策略中选取磁链模型为可调模型进行实验。图8所示为内转子在基于磁链可调模型的SM-MRAS无传感器控制下的实验波形，图8a为估计转速、实际转速及A相电流波形，图8b为转子估计位置及实际位置，由图8可看出估计转速有一定的毛刺，电流幅值波动较大，且估计位置有一定的脉动，即存在抖振现象。图9所示为采用饱和函数转速估算切换方法的改进SM-MRAS控制下的内转子实验波形，图9a所示估计转速平滑，波动小，与实际转速吻合度高，且电流波形正弦度高。图9b可看出该控制策略下能准确估计转子位置，且估计位置无脉动，即消除了未改进SM-MRAS控制策略引起的抖振现象。且对比图8a与图9a，可看出改进型的SM-MRAS相较于传统SM-MRAS，转速响应更快，转速突变时跟踪给定转速需要的时间较短。

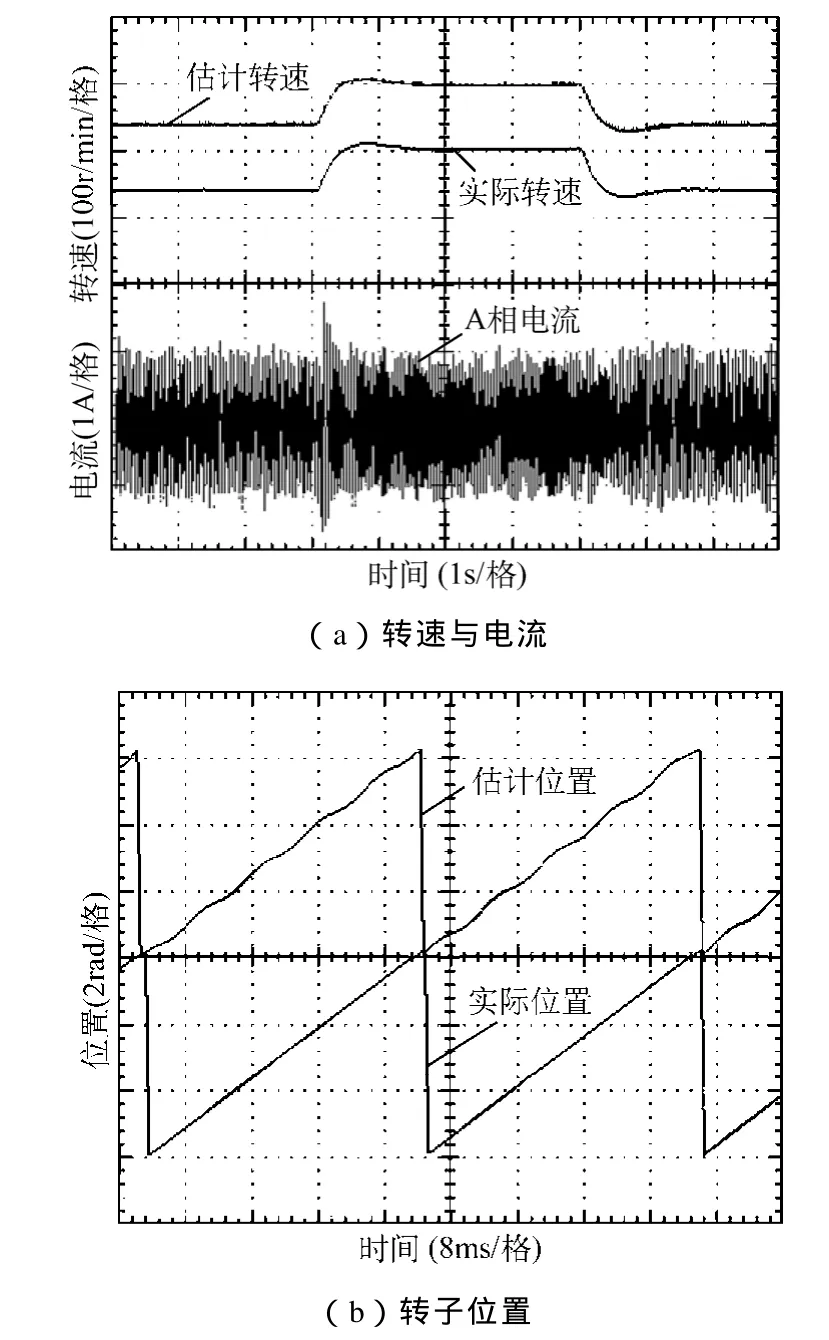
图8 基于磁链可调模型的SM-MRAS实验波形Fig.8 Experimental waveforms of SM-MRAS with the flux linkage adjustable model

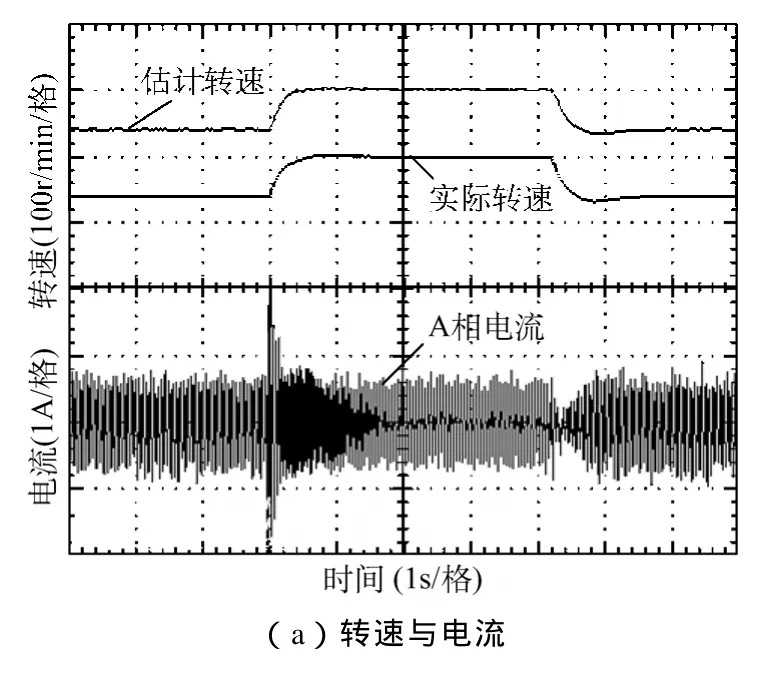
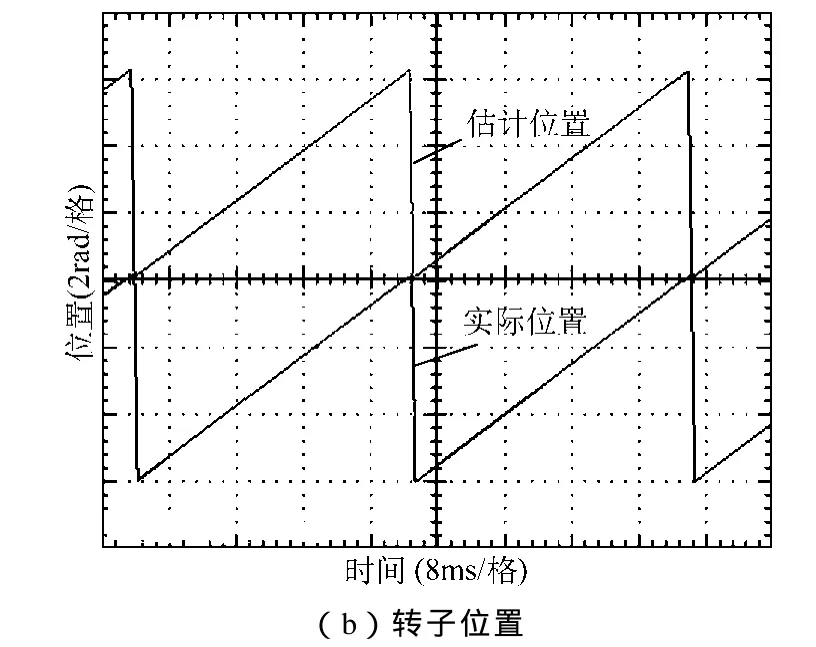
图9 基于磁链可调模型的改进型SM-MRAS实验波形Fig.9 Experimental waveforms of improved SM-MRAS with the flux linkage adjustable model

通过上述空载实验的验证，可看出基于磁链可调模型的采用饱和函数转速估算切换方法的改进型SM-MRAS策略能很好地实现内转子无传感器控制。为进一步验证该无传感器控制策略的性能，对内转子进行加载测试，并中途进行负载突变，内转子转速控制为200r/min。内转子在该无传感器控制策略下加载时的实验波形如图10所示。图10a所示为内转子估计转速、实际转速、A相绕组电流及估计转子位置。图10b所示为A相绕组电流及估计转子位置在短时间的波形图。从实验图上可看出实际转速与估计转速吻合，在负载突变时转速经过微小波动后即恢复正常，且绕组电流较正弦，估计转子位置稳定、无脉动。

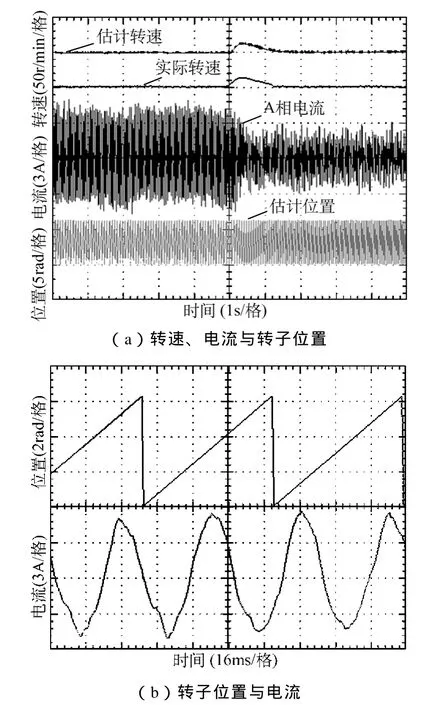
图10 内转子加载实验波形Fig.10 Experimental waveforms of the inner rotor with load

在内转子加载实验成功的基础上，采用异步电机模拟风力机，驱动外转子转动，同时控制内转子转速不变，并加载。实验过程中外转子转速从50r/min变化到35r/min再到15r/min，控制内转子转速保持200r/min不变，内外转子转速差则会变化，实验波形如图11所示。图11a展示了内转子实际转速、内外转子转速差及内转子电流，可见内转子转速保持恒定，内外转子转速差（即此时无位置估计转速）能跟踪给定值，A相绕组电流平稳，且从图11b中看出内转子估计转子位置无脉动，A相电流正弦度较高。上述实验结果表明了基于磁链可调模型的改进型SM-MRAS策略能良好地实现双功率流风力发电系统PM-EVT电机内转子的无位置控制。

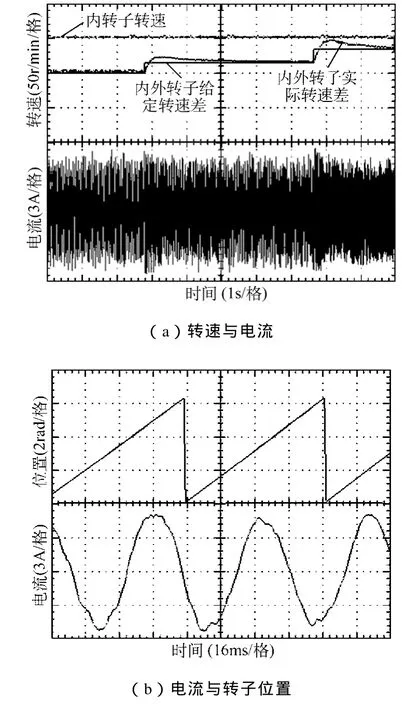
图11 外转子转动时内转子加载实验波形Fig.11 Experimental waveforms of the inner rotor with load when the outer rotor is rotating

5 结论

本文针对用于双功率流风力发电系统的电气无级变速器，提出了一种新型的改进型滑模变结构模型参考自适应无传感器控制方法，通过原理分析和实验研究表明：

（1）通过将滑模变结构算法取代传统模型参考自适应方法中的PI环节，使无传感器控制结构更简单，参数选择更便捷，同时达到了良好的转速估计效果。

（2）同时针对传统滑模变结构算法引起的抖振现象，本文采用的饱和函数转速切换估计算法有效地消除了这一现象，同时可省略原本所需的低通滤波器，提高转速估计速度。

[1] Hoeijmakers M J,Ferreira J A.The electrical variable transmission[J].IEEE Transactions on Industry Applications,2004,42(4):1092-1100.

[2] Xu L Y.Dual-mechanical-port electric machines-a new concept in design and analysis of electric machines[C].IEEE International Conference on Industry Applications,Columbus,2005:2828-2834.

[3] Cheng Y,Trigui R,Espanet C,et al.Specifications and design of a PM electric variable transmission for Toyota PriusⅡ[J].IEEE Transactions on Vehicular Technology,2011,60(9):4106-4114.

[4] Kim J,Kim T,Min B,et.al.Mode control strategy for a two-mode hybrid electric vehicle using electrically variable transmission(EVT)and fixed-gear mode[J].IEEE Transactions on Vehicular Technology,2011,60(3):793-803.

[5] 程明,花为.电气无级变速双功率流风力发电组:中国,ZL200710019235.X[P].2010-05-19.

[6] Sun X,Cheng M,Hua W,et al.Optimal design of double-layer permanent magnet machine for wind power application[J].IEEE Transactions on Magnetics,2009,45(10):4613-1616.

[7] Sun X,Cheng M,Zhu Y,et al.Application of electrical variable transmission in wind power generation system[J].IEEE Transactions on Industry Applications,2013,49(3):1299-1307.

[8] 李志强,夏长亮,陈炜.基于线反电动势的无刷直流电机无位置传感器控制[J].电工技术学报,2010,25(7):38-44.Li Zhiqiang,Xia Changliang,Chen Wei.A position sensorless control strategy for BLDCM based on line back-EMF[J].Transactions of china Electrotechnical Society,2010,25(7):38-44.

[9] 王大方,刘智祺,金毅,等.基于反电动势积分法的无位置传感器直流无刷电机试探性起动研究[J].电工技术学报,2012,27(12):178-184.Wang Dafang,Liu Zhiqi,Jin Yi,et al.Tentative strategy of starting sensorless BLDCM with the method of integrating the back EMF[J].Transactions of China Electrotechnical Society,2012,27(12):178-184.

[10]刘颖,周波,冯瑛,等.基于脉振高频电流注入SPMSM低速无位置传感器控制[J].电工技术学报,2012,27(7):139-145.Liu Ying,Zhou Bo,Feng Ying,et al.Sensorless control of SPMSM based on high frequency current signal injection in the direct axis at low and zero speed[J].Transactions of China Electrotechnical Society,2012,27(7):139-145.

[11]张猛,肖曦,李永东.基于扩展卡尔曼滤波器的永磁同步电机转速与磁链观测器[J].中国电机工程学报,2007,27(36):36-40.Zhang Meng,Xiao Xi,Li Yongdong.Speed and flux linkage observer for permanent magnet synchronous motor based on EKF[J].Proceedings of the CSEE,2007,27(36):36-40.

[12]程帅,姜海博,黄进,等.基于滑模观测器的单绕组多相无轴承电机的无位置传感器控制[J].电工技术学报,2012,27(7):71-77.Cheng Shuai,Jiang Haibo,Huang Jin,et al.Position sensorless control based on sliding mode observer for multiphase bearinglessmotorwith single setof windings[J].Transactions of China Electrotechnical Society,2012,27(7):71-77.

[13]王高林,张国强,贵献国,等.永磁同步电机无位置传感器混合控制策略[J].中国电机工程学报,2012,32(24):103-109.Wang Gaolin,Zhang Guoqiang,Gui Xianguo,et al.Hybrid sensorless control strategy for permanent magnet synchronous motors[J].Proceedings of the CSEE,2012,32(24):103-109.

[14]年珩,李嘉文,万中奇.基于参数在线辨识的永磁风力发电机无位置传感器控制技术[J].中国电机工程学报,2012,32(12):146-154.Nian Heng,Li Jiawen,Wan Zhongqi.Sensorless control technique of PMSG for wind power application based on on-line parameter identification[J].Proceedings of the CSEE,2012,32(24):103-109.

[15]王庆龙,张崇巍,张兴.基于变结构模型参考自适应系统的永磁同步电机转速辨识[J].中国电机工程学报,2008,28(9):71-75.WangQinglong,Zhang Chongwei,ZhangXing.Variable-structure MRAS speed identification for permanent magnet synchronous[J].Proceedings of the CSEE,2008,28(9):71-75.

[16]苏建勇,李铁才,杨贵杰.PMSM无位置传感器控制中数字滑模观测器抖振现象分析与抑制[J].电工技术学报,2009,24(8):58-64.Su Jianyong,Li Tiecai,Yang Guijie.Chattering phenomenon analysis and suppression of sliding mode observer in PMSM sensorless control[J].Transactions of china Electrotechnical Society,2009,24(8):58-64.[17]Comanescu M,Xu L Y.Sliding-mode MRAS speed estimators for sensorless vector control of induction machine[J].IEEE Transactions on Industrial Electronics,2006,25(1):146-153.