自适应三维分数阶微分增强算法

余 婷，李明晶，赵九龙，马 瑜，李 爽

(1.宁夏大学 研究生院，宁夏 银川 750021；2.长春大学 电子信息工程学院，吉林 长春 130022；3.上海交通大学 图像处理与模式识别研究所，上海 200240)

自适应三维分数阶微分增强算法

余 婷1，李明晶2，赵九龙1，马 瑜1，李 爽3

(1.宁夏大学 研究生院，宁夏 银川 750021；2.长春大学 电子信息工程学院，吉林 长春 130022；3.上海交通大学 图像处理与模式识别研究所，上海 200240)

针对三维数字图像在重构预处理阶段分辨率不高、模糊等影响重构精度的问题，提出了基于自适应三维分数阶微分的增强算法。在将二维分数阶微分推广应用至三维的基础上，尝试性地基于图像自身梯度信息和相邻体素间梯度变化构造了自适应三维分数阶微分阶数，并给出了三维离散滤波模板。利用三维切片图像自身梯度信息解决了不同属性图像及不同图像区域最优的分数阶微分阶数不同的问题，提高了实时处理效率。将自适应增强算法应用至三维边缘曲面追踪算法，可以重构出精度更高的三维数字图像。

三维分数阶微分；自适应增强；梯度；重构；边缘曲面追踪

三维数字图像相比于二维数字图像有更大的参考和利用价值，因此三维数字图像处理近年来得到了广泛的研究。三维数字图像的成像方式多为利用计算机断层扫描(Computerized Tomography， CT)和核磁共振(Nuclear Magnetic Resonance， NMR)等手段获取多组二维切片图像，利用科学可视化[1-2]方法对多组二维切片图像构成的三维切片进行三维重构。在重构与处理阶段，有必要对模糊不清或分辨率不高的切片图像进行增强预处理操作，以突显人们更感兴趣的区域或细节信息。

分数阶微积分理论已经有很长的历史，周激流、蒲亦非等将分数阶微积分引入图像处理领域，近年来有较多科研成果出现[3-5]。近年来分数阶微积分在图像处理中的应用越来越广泛。由于分数阶微分可以在增强高频信号的同时，极大地非线性保留中低频信号，所以相比于整数阶微分，分数阶微分可以增强图像高频细节的同时，可以很好地保留中低频的纹理和灰度变化不大的区域。多数分数阶微积分的算法在图像处理当中多应用于二维数字图像，本文在将分数阶微分推广至三维图像(信号)的基础上，继续改进算法，提出基于三维图像局部梯度和相邻体素梯度变化的自适应三维分数阶微分增强算法，实验结果表明提出的算法可以取得较好三维增强效果。

1 分数阶微分对信号作用分析

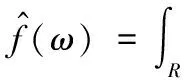
(1)

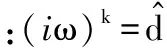
(2)

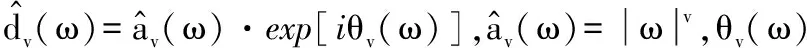
图1 分数阶微分对信号的作用曲线

由图1可以看出，在高频或超高频部分即信号频率ω≫1 时，整数阶微分和分数阶微分对高频信号都有提升作用，且整数阶微分的提升效果更强；在信号低频部分即信号频率ω≪1时，整数阶微分和分数阶微分对信号低频部分都有削弱作用，且整数阶微分削弱幅度更大，如二阶的整数阶微分的信号幅值已经趋近于0，而分数阶微分仍能一定程度地保留原有信号；在信号中频部分即频率接近于1时，分数阶微分作用后的信号更接近原信号幅值。由以上分析可以得知，相比于整数阶微分，分数阶微分在可以提升信号高频成分的同时较好地保留信号中低频成分，而且可以更大程度地保留信号低频和甚低频部分，而在数字图像增强处理中，高频信号对应需要增强的边缘信息，中高频信号可以看作纹理细节信息，低频信号可以看作原图像中灰度改变程度不大的平滑区域。进而在用分数阶微分时可以在增强图像边缘等高频信息的同时，最大程度地对原平滑部分做保留。

2 三维分数阶微分定义及模板

基于Grümwald-Letnikov定义的二维分数阶微分的后向差分表达式如下[4-5,7-8]

(3)

(4)

与一维分数阶微分算子扩展到二维相似，二维分数阶微分算子在考虑三维空间信息的情况下，基于离散傅里叶变换的可分离性，也可扩展到三维。根据式(3)和式(4)，以各坐标轴负方向为例可得到三维函数f(x,y,z)连续分数阶微分算子

(5)

(6)

(7)

首先给出大小为5×5×5的三维分数阶微分离散模板,如图2所示。

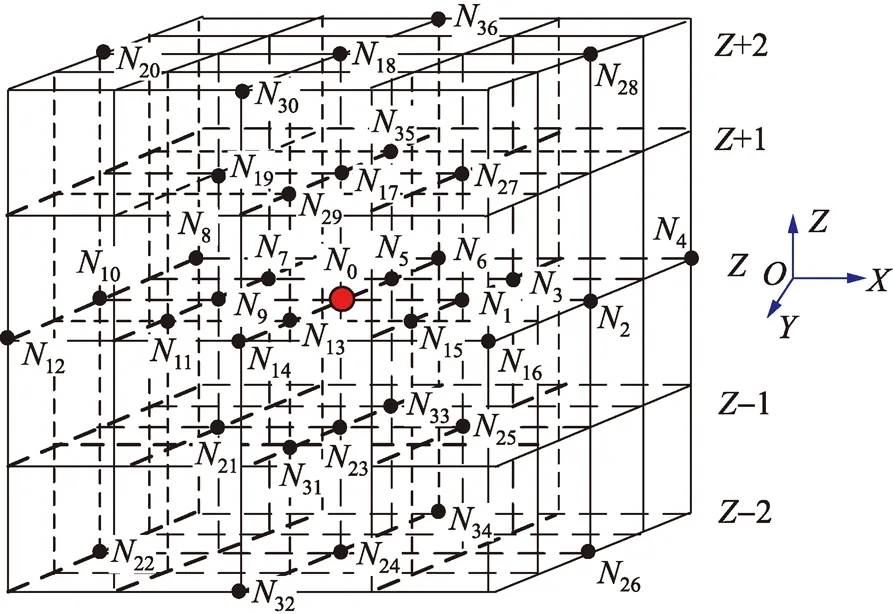
图2 三维分数阶微分离散模板

图2为5×5×5大小的三维分数阶微分离散模板，图中有5层切片，分别为中心待处理体素所在的Z层及其上方的 Z+1 层，Z+2层和下方的Z-1层，Z-2层。三维模板构成可以理解为以N0为中心，XY平面、XZ平面、YZ平面立体组合而成，也即3个二维模板组成一个三维离散模板。如图所示选取与中心体素(centrevoxel)相邻的18个方向为三维离散模板的有用体素，在XY平面即Z层，在X轴和Y轴，及X轴Y轴对角线的8个方向上，有N1～N16共16个体素点；在XZ平面从Z-2至Z+2的5层切片中，有N1,N2，N27，N28，N17，N18，N19，N20，N9，N10，N21，N22，N23，N24，N25，N26共16个体素点，在YZ平面同样有N5，N6，N35，N36，N17，N18，N29，N30，N13，N14，N31，N32，N23，N24，N33，N34共16个体素点。

按照式(5)～(7)，模板中对应位置系数如下

(8)

三维分数阶微分模板取18个方向， 18个方向的卷积结果如下

(9)

在计算卷积结果前要对三维离散模板内各系数做归一化处理

(10)

将各系数带入式(9)，求得18方向的卷积值后求和，如式(11)所示，最终D(i,j,k)即为三维分数阶微分处理后的新体素值。

(11)

3 自适应微分阶数构造

图像中有很多反映自身特征的信息，如灰度值、像素梯度值等。梯度在图像中反映了像素幅值变化的程度，利用数字图像的灰度值梯度变化，进一步细化三维图像灰度值的梯度和相邻体素间梯度变化对于数字图像的影响，构造基于梯度信息的自适应三维分数阶微分阶数，应用三维分数阶微分模板对三维图像进行遍历卷积操作，达到增强图像有用信息拉伸图像对比度的目的。

在三维数字图像中，各体素点最小距离为单位1，三维数字图像的体素值即为离散的三维函数值，为便于数值计算和程序实现，对于离散的三维函数采用前向差分来计算梯度。

一阶梯度不能全面反映三维数字图像梯度变化，先在三维模板中定义梯度本身的变化为Cg，如图2三维分数阶离散模板所示，取步长为1和前向差分来计算梯度变化。

以图2模板中待处理体素点X轴正方向为例，计算此方向上N0点的梯度，N0为要处理的体素点，N1，N2为Z层切片上X轴正方向上半径为1和2的相邻两体素点。

设f(x,y,z) 为当前体素，显然N1点为f(x+1,y,z)，N2点为f(x+2,y,z)。

当前待处理体素点N0的梯度为GN0=f(x+1,y,z)-f(x,y,z)，相邻点N1的梯度为GN1=f(x+2,y,z)-f(x+1,y,z)。

则对于N0点在此方向上的梯度变化模值为Cg1，即N1与N0点梯度差值。如前文所述，模板中共有18个方向，Cg1表达式如下

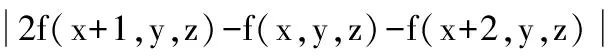
(12)

以步长为2求得当前体素点在N1，N2方向的梯度模值为G1，同样在上述模板中另有17个方向，G1表达式如下

(13)

各取18个方向中当前体素点梯度变化的最大值和梯度最大值进行后续计算，则表达式如下

(14)

由于指数模型在底数大于1指数为负时，整体指数值范围在0～1之间，符合分数阶微分的阶数要求。由于此特性，采用以e为底的指数模型，当指数(次方)在不大于0时，指数整体值为不大于1的正数，满足分数阶微分对阶数的要求，因此利用此特性，利用前述梯度变化和梯度值构造指数模型如下

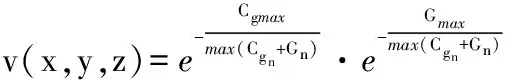
(15)

式(15)中利用当前体素点梯度值和梯度变化模值构造了三维自适应分数阶微分阶数，对于不同的体素点，其所用的微分阶数不同，且完全受自身体素梯度变化影响。对于三维数字图像来说，当前处理区域为平滑区域时，式(15)中指数次方的分子也即梯度变化和体素梯度值均较小，所得v会相对较大，由分数阶微分对信号作用分析可知，当信号频率较小时，即当频率为低频时，较大的微分阶数会相对降低低频的幅值，这样可以达到拉伸平滑区域体素与中高频区域的对比度，达到增强的目的。对于中高频部分的纹理细节和边缘信息，梯度变化和灰度梯度值都较大，所得v比低频平滑部分略小，仍可对高频信息进一步增强，这样从定性角度分析，以上自适应三维分数阶微分可以依据图像自身梯度信息对三维图像自适应增强。

4 改进的边缘曲面重构算法

4.1 边缘曲面追踪算法

三维边缘曲面追踪算法数学模型为[9-10]

(16)

4.2 基于自适应三维分数阶微分增强的边缘曲面追踪算法

基于自适应三维分数阶积分增强的边缘曲面追踪算法步骤如下：

1)利用自适应三维分数阶微分对采集的三维切片图像进行增强；

2)利用本节第一部分中介绍的算法追踪三维边缘曲面；

3)计算三维边缘曲面片并将其三角片化；

4)通过计算机图形学技术可视化三维边缘曲面。

设三维图像(数据)f(x,y,z)经自适应三维分数阶微分增强后变为D(x,y,z)，从增强后的D(x,y,z)追踪边缘曲面，基于自适应三维分数阶微分增强的边缘曲面追踪算法如下(对于边缘曲面追踪算法详细描述见文献[9-10])

(17)

5 实验结果及分析

在构造了自适应三维分数阶微分阶数后，利用边缘曲面追踪算法对已经过分数阶微分增强的D(x,y,z)通过VC++2010和OpenGL进行重构显示，得到增强后的三维数字图像。本实验硬件环境CPU为Inteli3，2GHz，2GbyteRAM。

在二维数字图像的分数阶微分增强中，多数算法均只采用视觉定性分析来衡量算法的有效性，鉴于较成熟的三维经典算法较少，本章实验结果与固定阶分数阶微分增强效果作对比，并采用视觉定性分析和图像信息熵(comentrypy)结合评价增强效果。

香农首先提出信息熵的概念[11]。信息熵可以用来反映信息中信息量的多少，是信息论学科中的一个较为重要的概念[12]，显然信息熵越大则其中包含的有用信息量越大。其定义如下

(18)

式中：p(x)为事件x发生的概率。在三维图像中，图像的信息熵可以表示为如下形式

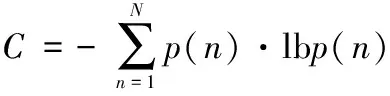
(19)

式中：p(n)为像素级别n出现的概率，也可理解为三维图像中体素点f(x，y，z)出现的概率；N为像素级别数，如8位图像为256。

实验首先选取数据规模为125×125×34的龙虾图像，切片图像有34层，每层长于宽均为125。

图3给出了龙虾图像经不同阶数增强后，利用边缘曲面追踪算法重构后的结果。由于本文实验源切片图像本身灰度较低，且灰度变化范围较小，故图像细节变化不是特别明显，在图3a的待增强图像中选取了3个区域进行着重对比分析，图3c和图3e分别经0.5阶和0.7阶增强后，重建后三维图像的I区和II区均产生了噪声碎片，且图3e表面整体已经很粗糙，没有达到较好的增强效果。图3d经本文算法增强后，在III区对龙虾爪的纹路等区域较好地进行了增强，且没有图3c和图3e中的噪声。通过表1中的信息熵值分析可知， 0.7阶微分增强结果虽然熵值较大，其原因是增强出的噪声干扰了熵值的计算，本文算法在获得较好视觉效果的同时，也获得了不错的信息熵值。

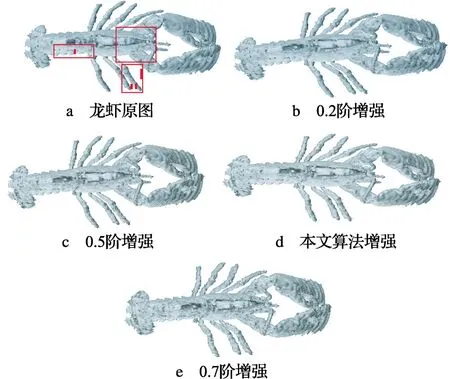
图3 不同分数阶微分阶数增强龙虾图像

分数阶微分阶数图像信息熵0228205284本文自适应阶数28507289

另一组实验针对数据规模为160×120×29的牛颈骨三维切片进行增强，切片共有29层，每层大小为160×120，同样随机选取固定阶次为0.2阶，0.5阶及0.8阶的分数阶微分增强效果与本章自适应增强进行对比。增强后利用边缘曲面追踪算法重构结果如图4所示。

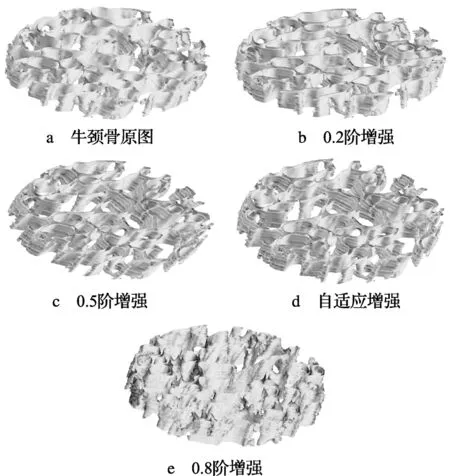
图4 牛颈骨分数阶微分增强结果

图4给出了牛颈骨经不同阶次分数阶微分增强后的结果，图4a原图像中骨头的纹路不是很明显，对比度不高，所含细节较少。图4b～图4e均对原图进行了不用程度的增强，图4b中0.2阶固定阶次的分数阶微分增强幅度明显不够，细节信息仍然不够明显，0.8阶的微分增强图像出现了过增强效果，整体灰度值较亮，仍然不能较好地体现出对比度。可以看出本文算法自适应增强后，与0.5阶增强结果较为接近，但由于利用了图像自身梯度信息和梯度变化，自适应地拉伸了灰度变化平缓区域与中高频的对比度，所以图像的纹路等细节更加明显，也较好地达到了增强的效果。表2的信息熵值也可验证以上观点。随机选取的3个固定阶次分数阶微分中，0.8阶增强后信息熵值较大，但是其图像本身给人的视觉感受并不是最好，整体骨头纹路难以看清。本文算法在兼顾信息熵的同时得到了对比度明显且细节较多的增强结果。

表2 分数阶微分增强牛颈骨图像信息熵

分数阶微分阶数图像信息熵0239505400本文自适应阶数40608410

6 结语

目前多数分数阶微积分的算法都应用在二维数字图像，针对三维数字图像的增强算法较少。本文尝试性地在利用图像自身灰度值的梯度变化和梯度值本身，构造了自适应三维分数阶微分阶数的指数模型，利用三维分数阶微分离散模板对三维切片图像进行遍历卷积，旨在利用图像自身梯度特性有目的地增强感兴趣区域。通过实验分析可见，一定程度上实现了自适应增强，对于灰度变化平缓的区域，实现了算法设计之初适当降低平缓区域幅值，拉开与细节等中频信息的对比度并增强中高频信息的目的，通过信息熵的对比，提出的算法也能基本接近最优的固定阶次分数阶微分增强后的信息熵值，验证了提出算法的有效性。

[1] 唐泽圣. 三维数据场可视化[M].北京：清华大学出版社，1999.

[2] 刘晓强. 科学可视化的研究现状与发展趋势[J]. 工程图学学报，1997 (2)：124-130.

[3] 马瑜，余婷，赵九龙，等. 一种改进的自适应分数阶积分图像去噪算法[J]. 电视技术，2014，38(19)：36-40.

[4] 蒲亦非. 将分数阶微分演算引入数字图像处理[J]. 四川大学学报：工程科学版，2007，39(3)： 124-132.

[5] 张涌，蒲亦非，周激流. 基于分数阶微分的图像增强模板[J].计算机应用研究， 2012，29(8)：3195-3197.

[6] TAO Ran， DENG Bin， WANG Yue. Research progress of the fractional Fourier transform in signal processing [J]. Science in China Series F， 2006，49(1)：1-25.

[7] OLDHAM K B， SPANIER J. The fractional calculus [M]. New York： Academic Press， 1974.

[8] PODLUBNY I.Fractional differential equations [M]. New York：Academic Press，1999.

[9] WANG L， BAI J， YING K. Adaptive approximation of the boundary surface of a neuron in confocal microscopy volumetric images[J]. Medical and Biological Engineering and Computing，2003，41(5)： 601-607.

[10] 马瑜，王利生，唐渊圆. 三维图像中阶梯型边缘曲面的追踪算法[J]. 计算机辅助设计与图形学学报，2007，19(3)：329-333.

[11] SHANNON C E. A mathematical theory of communication[J]. Bell System Thchnical，1948，27(1)：1-54.

[12] SHANBHAG A G. Utilization of information measure as a means of image thresholding[J]. CVGIP： Graphical Models and Image Processing， 1994， 56(5)： 414-419.

[13] 李晓阳， 王明泉， 王玉， 等. 基于灰度选择法的医学图像可视化算法研究[J]. 电视技术，2014，38(3)：16-18.

[14] 潘翔， 陈国栋. 基于复用计算的三维肝脏内部可视化方法研究[J]. 电视技术，2014， 38(11)：53-56.

[15] 马瑜，赵九龙，余婷，等. 基于三维分数阶微分增强的边缘曲面重构算法[J]. 光子学报， 2014，43(10)：27-34.

责任编辑：闫雯雯

Adaptive 3D Fractional Differential Enhancement Algorithm

YU Ting1, LI Mingjing2, ZHAO Jiulong1, MA Yu1, LI Shuang3

(1.Graduate School, Ningxia University, Yinchuan 750021, China； 2. School of Electronic Information Engineering,Changchun University,Changchun 130022,China； 3. Institute of Image Processing and Pattern Recognition, Shanghai Jiaotong University, Shanghai 200240, China)

Three dimensional(3D) digital slice images are usually not clear enough to be reconstructed. An adaptive enhancement algorithm based on 3D fractional differential is put forward. On the basis of extending 2D fractional differential to 3D, the adaptive 3D fractional order is constructed using the gradient and the variation of neighbor gradient, the 3D discrete filtering mask is also provided. The proposed algorithm can not only solve the problem of different images’ best fractional orders are different, but also increasing the enhancement efficiency largely. Adding the adaptive enhancement algorithm to 3D edge surface tracking algorithm can reconstruct higher accuracy 3D images.

3D fractional differential; adaptive enhancement; gradient; reconstruction; edge surface tracking

国家科技支撑计划项目(2012BAF07B00)； 2012年宁夏自治区科技攻关资助项目(2012ZYG011)；吉林省教育厅“十二五”科学技术研究资助项目(2014302)

TN911.73

A

10.16280/j.videoe.2015.20.001

余 婷(1990— )，女，硕士，主要研究方向为分数阶微积分；

李明晶(1977— )，女，副教授，博士，主要研究方向为图像融合；

赵九龙(1989— )，本文通信作者，硕士生，主要研究方向为数字图像增强及去噪、分数阶微积分；

马 瑜(1974— )，教授，博士，主要研究方向为计算机视觉与模式识别；

李 爽(1993— )，硕士生，主要研究方向为虚拟全景图像增强技术研究。

2015-04-23

【本文献信息】余婷，李明晶，赵九龙，等.自适应三维分数阶微分增强算法[J].电视技术,2015，39(20).