基于块的Mean-shift跟踪算法
陈 柱,李子印,朱明凌
(中国计量学院 光学与电子科技学院,浙江 杭州 310018)
基于块的Mean-shift跟踪算法
陈 柱,李子印,朱明凌
(中国计量学院 光学与电子科技学院,浙江 杭州 310018)
针对传统Mean-shift跟踪算法在目标发生遮挡和形态变化时跟踪性能下降的缺点,提出了一种基于块的Mean-shift跟踪算法,该算法主要特点有:1)将跟踪目标平均分块,每小块独立进行传统Mean-shift跟踪,利用小块跟踪未被遮挡的目标部分;2)跟踪检测器检测目标小块跟踪的有效性,筛选出无效跟踪的目标小块,解决了目标分块造成跟踪性能下降的问题;3)归一化互相关检测器和邻域一致检测增加了对目标空间信息的检测,弥补了Mean-shift算法的局限性,增加了跟踪的鲁棒性。实验表明,该算法在目标发生遮挡和形态变化时仍然可以有效地实现跟踪。
目标跟踪;目标遮挡;形态变化;目标分块;Mean-shift跟踪算法
运动目标跟踪已经被广泛应用到社会生活的各个方面,但在实际应用中仍面临着诸多的挑战,如目标遮挡、形态变化等[1-3]。Mean-shift跟踪算法是一种基于核概率密度估计的无参数算法,具有实时性强、计算量小和跟踪精度高等特点,成为典型的目标跟踪算法。但传统Mean-shift跟踪算法的跟踪窗口保持不变,这样当目标发生旋转或尺度变化时,其跟踪性能将会受到很大的影响。因此,研究人员不断尝试其改进算法[4-7],文献[4]采用上下二分的方法跟踪运动目标,但该方法只适用于柱状对象;文献[6]采用了七部分的分块方法,用平均值的方法代表每一个跟踪小块的Bhattacharyya系数,但该方法没有考虑每个目标小块相似度的变化对运动目标总体相似度的影响。
基于本文提出了一种基于块的Mean-shift跟踪算法,首先将目标平均分块,各子块分别使用Mean-shift跟踪算法进行跟踪,然后通过检测器表决各子块是否正确跟踪,利用正确跟踪的子块更新目标,从而实现跟踪。
1 Mean-shift跟踪算法
Mean-shift跟踪算法是一种基于概率密度估计的无参数算法,其在概率密度函数中快速迭代收敛于局部极大值,在每一次迭代过程中都是朝着最优值进行的,是一种高效的实时跟踪算法[8-10]。
1.1 目标模型
首先获取运动目标的初始位置,然后对获得的区域建立目标模型qu,假设其中有n个像素,{zi}i=1,2,…,n分别表示每个像素的位置,对获得的目标区域的灰度颜色空间进行均匀的划分,便可以得到有m个相等区间构成的灰度直方图,这样目标模型qu的概率密度可表示为

(1)

(2)
(x0,y0)代表目标的中心坐标,C代表归一化系数,其值可表示为
(3)
1.2 候选模型
与目标模型表示类似,设{zi}i=1,2,…,n是候选目标区域的像素位置,候选区域的目标中心位置坐标为f,则候选模型的概率密度可表示为
(4)
其中,h为核函数窗口的大小,决定着权重的分布。
1.3 Bhattacharyya相关系数
用来表示目标模型和候选模型的相似度,可定义为
(5)
ρ(p,q)越大,则目标模型和候选模型越相似。
1.4 目标定位
为了使ρ(p,q)最大,对其进行泰勒展开,得到Bhattacharyya相关系数的近似表达
(6)
其中,ωi可表示为
(7)
ρ(p,q)的其他参数都已确定,只有ωi的值随f的变化而变化,这样求极大值的过程就可以通过目标候选区域的中心向目标真实区域的中心的Mean-shift迭代方程完成
(8)
其中,g(x)=K′(x)是核函数K(x)的影子核。Mean-shift方法即从fk起向目标模型和候选模型颜色变化最大的方向不断地移动,直到最后2次移动的距离小于阈值,便找到了当前帧的目标位置,并以此作为下一帧的起始搜索窗口的中心,如此反复,即可不断实现对目标的跟踪。
2 基于块的Mean-shift跟踪算法
Mean-shift的跟踪在实际应用中存在一些缺点。首先,Mean-shift跟踪算法过分依赖运动目标的颜色信息,而忽略了运动目标的空间信息,这样当颜色相似的物体重叠时,便可能导致对运动目标跟踪的失败;再次,当运动目标发生形态发生变化时,容易造成跟踪失败;最后,当运动目标发生遮挡时,Mean-shift算法获得的运动目标的位置坐标有可能出现错误,从而导致跟踪失败。
针对实际复杂环境中出现的目标遮挡和形态变化的问题以及上述Mean-shift跟踪算法存在的不足之处,本文提出了一种基于块的Mean-shift跟踪算法。
2.1 分块跟踪
设运动目标的区域为M,将M平均分割为x×y个目标小块,如图1所示,每个小块的图像尺寸不能过小,因为Mean-shift跟踪算法本身是基于颜色直方图的,当每个小块的尺寸过小时,目标所包含的信息量就会很少,容易造成跟踪的失败,另外尺寸过小也不能适应运动目标的突变等运动。所以,本文采用把目标小块分割成不小于10×10像素的方法,对分块后的每一个目标小块独立地进行Mean-shift跟踪,跟踪前使用卡尔曼滤波预测目标位置,并在目标位置的基础上确定对应目标小块的具体位置信息,以此作为跟踪的起点。这样做的好处是:目标遮挡、形态变换的问题主要表现为目标信息的丢失,每一小块独立跟踪,并分别判断是否跟踪有效,以此来判断目标的局部信息是否丢失,这样当目标出现部分遮挡或者形态变化时,可以通过跟踪有效的目标小块来实现对目标的跟踪。

图1 运动目标分块
然而运动目标往往由几个层次的颜色区域组成,均匀分块会把同一个颜色区域分为不同的块,以一辆汽车为例,车辆车身的颜色几乎是一致的,将汽车进行均匀分块可能导致有些块与块之间的图像信息是相似的,这样目标小块就有可能无法跟踪到真实的目标区域,针对该问题,本文加入了跟踪检测器,通过跟踪检测器来检测每一小块是否跟踪有效。
2.2 跟踪检测器
本文的跟踪检测器由归一化互相关检测器和邻域一致检测器组成,这两种检测器分别按照各自的方法对目标小块进行检测,只有当2个检测器都判断为正确时,目标小块才能被认为是跟踪有效的小块,否则剔除。
归一化互相关检测器是用NCC(NormalizedCrossCorrelation)算子[11]来衡量原目标小块和跟踪后得到的区域小块之间的像素相似程度,NCC算子是一种经典的图像匹配算子,表征2幅图像的相似程度,其中I1,I2是尺寸为m×n的两幅图像
(9)
NCC的取值范围为0~1,其值越大,则表示2幅图像越相似。
归一化互相关检测器对每一个目标小块依次进行检测,计算每个目标小块与跟踪后得到的目标区域的NCC值,若该值大于设定的阈值Th,认为目标小块有效,否则认为是无效的目标小块。

(10)
对于阈值Th的取值,本文引入平均相关系数Rs,Rs表示两幅图像的像素灰度平均相似程度,IM为运动目标图像,IP为当前帧图像,则Rs可表示为
(11)
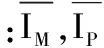
邻域一致检测器的假设前提是分块后的目标小块在各自跟踪后,相邻目标小块的位移矢量是相似的。因此,邻域一致检测器通过检测每个目标小块与其四邻域的目标小块的跟踪位移矢量是否相符,若位移矢量不相符,则认为该目标小块是无效的块。
跟踪检测器的作用是对目标分块跟踪后进行判断,检测出无效跟踪的目标小块,筛选出具有较高鲁棒性的目标小块作为目标跟踪的依据。传统的Mean-shift跟踪缺少了对目标空间信息的描述,而归一化互相关检测器通过比较每一个目标小块相邻两帧整体像素的相似程度来做出判断,只有当目标小块相邻两帧整体像素空间分布具有较高的相似度时才能通过该检测器,邻域一致检测器通过检测目标小块的位移矢量来做出判断。因此,这两种检测器都能够对目标的空间信息进行检测,在一定程度上弥补了Mean-shift跟踪的不足之处。
2.3 算法实现步骤
本文算法实现步骤如下:
1)将当前帧的运动目标M平均分成x×y个目标小块,使用卡尔曼滤波器预测运动目标位置,并在目标位置的基础上确定对应目标小块的具体位置信息。
2)对各目标小块分别进行Mean-shift跟踪。
3)计算运动目标的平均相关系数Rs,作为阈值Th,比较各目标小块的NCC值与阈值Rs的大小,如果NCC的值大于阈值,则保留目标小块,否则剔除。
4)统计保留下来的各目标小块跟踪后的位移矢量,比较每个小块与其四邻域小块的位移矢量,如果存在矢量夹角大于90°,则认为该目标小块跟踪突变,予以剔除,否则保留。
5)将跟踪检测器保留下来的目标小块作为跟踪依据,并更新运动目标M,作为下一帧跟踪的模型。
算法具体流程如图2所示。

图2 基于块的Mean-shift算法流程图
3 实验结果及分析
为了验证本文算法的性能,使用VS2010在Intel Core(TM)i3-2120 CPU 3.3 GHz,内存为2 Gbyte的计算机上,分别对传统Mean-shift跟踪算法、文献[6]算法和本文算法进行测试。
1)跟踪结果比较
实验1为行人的跟踪,其中目标行人伴随着遮挡变化,跟踪结果如图3所示。图3a为传统Mean-shift算法的跟踪结果,图3b为文献[6]算法的跟踪结果,图3c为本文算法的跟踪结果。在未发生遮挡时,传统算法、文献[6]算法和本文算法都能很好地进行跟踪,当目标发生遮挡时,由于传统 Mean-shift 跟踪算法缺少足够的目标信息,进而陷入局部极大值,从而使跟踪的结果产生较大的偏移,最终导致跟踪的失败;文献[6]算法采用了七部分的分块方法,用平均值的方法代表每一个跟踪小块的Bhattacharyya系数,能够在一定程度上实现跟踪,但跟踪窗口的中心与运动目标的中心有一定的偏差;本文算法由于采用了目标的分块跟踪,当目标发生部分遮挡时,可以对未被遮挡的目标很好地进行Mean-shift跟踪,并且每一帧目标小块的初始位置经卡尔曼滤波估计确定了其位置信息,这样跟踪后的目标小块经过跟踪检测器的检测后,有效的目标小块被保留下来,同时最终的跟踪结果整合了所有小块的跟踪信息,从而能够很好地实现跟踪。

图3 跟踪结果比较
实验2同样为行人的跟踪,其中目标行人的视角由远到近,跟踪结果如图4所示。其中,图4a为传统Mean-shift算法的跟踪结果,图4b为文献[6]算法的跟踪结果,图4c为本文算法的跟踪结果。由于传统Mean-shift算法在目标跟踪过

图4 跟踪算法比较
程中跟踪窗口的大小保持不变,这样在跟踪过程中目标模式总是使得Bhattacharyya系数在同样大小的跟踪窗口中达到局部最大,从而不能准确的实现跟踪;文献[6]算法采用了七部分的分块方法,用平均值的方法代表每一个跟踪小块的Bhattacharyya系数,这样跟踪窗口可以随着目标的变化而变化,从而能够很好地实现跟踪,但跟踪窗口的中心与运动目标的中心有一定的偏差;本文算法采用了目标的分块,对每个小块分别进行Mean-shift跟踪,当目标的视觉角度发生变化时,利用分割后的目标小块进行Mean-shift跟踪,并且每一帧目标小块的初始位置经卡尔曼滤波估计确定了其位置信息,这样跟踪后的目标小块经过跟踪检测器的检测后,有效的目标小块被保留下来,同时最终的跟踪结果整合了所有小块的跟踪信息,从而能够很好地实现跟踪。
2)跟踪成功率统计
为了更准确地统计跟踪结果的成功率,采用PASCALVOC标准[12]对运动目标跟踪的成功率进行统计,其示意图如图5所示。

图5 重合度计算示意图
其中,真实目标区域为Sa,跟踪结果区域为Sb,则跟踪结果与真实目标的重合度Rc可表示为二者交集与二者并集的面积之比,即
(12)
其中,area表示每个区域的面积,area(Sa∩Sb)表示两者的重叠面积,area(Sa∪Sb)表示两者的面积之和。对于每一帧的跟踪结果,如果Rc大于0.5,则代表跟踪成功;否则代表跟踪失败。
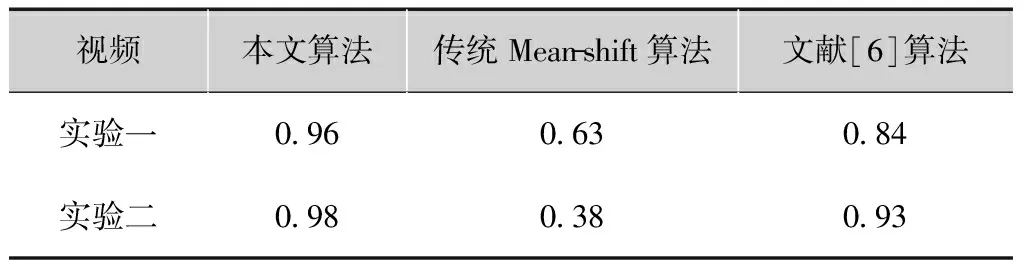
表1为本文算法、传统Mean-shift跟踪算法和文献[6]算法在两个实验视频中的跟踪成功率统计。从表中可以看出,本文算法在两个实验中都有很好的跟踪成功率。
表1 跟踪成功率统计
视频本文算法传统Mean-shift算法文献[6]算法实验一096063084实验二098038093
4 小结
针对传统Mean-shift跟踪算法在目标发生遮挡和形态变化时,跟踪性能下降的问题,本文提出了一种基于块的 Mean-shift跟踪算法,首先将目标平均分块,并利用卡尔曼滤波预测目标的位置,每一个目标小块分别独立地进行Mean-shift跟踪,然后通过跟踪检测器检测目标小块跟踪的有效性,进而对目标模型进行更新。实验表明,当运动目标发生遮挡或形态发生变化等复杂场景时,本文算法能够有效地实现跟踪,改善了传统Mean-shift跟踪算法的局限性,具有更高的鲁棒性,但本算法的运算复杂度还比较高,下一步可尝试改进分块的方法。
[1] 张钰婷,王沛,马燕,等. 改进的多特征融合粒子滤波视频跟踪算法[J].电视技术,2014,38(19):47-50.
[2] 刘雪琴,杨媛,李洁,等. 一种基于特征点的快速跟踪算法[J]. 电视技术,2013,37(5):34-37.
[3] 鲁超,滕国伟,邹雪妹,等. 一种适应运动前景的快速行人检测算法[J]. 电视技术,2015,39(1):113-117.
[4] OKUMA K,TALEGHANI A,DE F N,et al. A boosted particle filter: multi-target detection and tracking [C]// Proc of the European Conference on Computer Vision. Prague:IEEE Press,2004:28-39.
[5] 陈定坤,杨艳. 一种改进的Mean-shift运动目标跟踪算法[J]. 半导体光电,2015,36(1):160-164.
[6] MAGGIO E,CAVALLARO A. Multi-part target representation for color tracking[C]//Proc. IEEE Int. Conference on Image Processing. Genoa:IEEE Press,2005:729-732.
[7] 胡铟,杨静宇.基于分块颜色直方图的Mean-Shift跟踪算法[J].系统仿真学报,2009,21(10):2936-2940.
[8] 王田,刘伟宁,韩广良,等.基于改进MeanShift的目标跟踪算法[J]. 液晶与显示,2012,27(3):396-400.
[9] COMANICIU D, MEER P. Mean Shift: a robust approach toward feature space analysis[C]//Proc. IEEE Trans. Pattern Analysis and Machine Intelligence,2002,24(5):603-619.
[10] COLLINS R. Mean-Shift blob tracking through scale space[C]// Proc. IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE Press,2003,2:234-240.
[11] 杨通钰,彭国华.基于NCC的图像匹配快速算法[J]. 现代电子技术,2010(22):107-109.
[12] EVERINGHAM M,GOOL L,WILLIAMS C, et al. The Pascal Visual Object Classes (VOC) challenge [J]. International Journal of Computer Vision,2010,88(2):303-338.
陈 柱(1989— ),硕士生,主研图像处理、模式识别;
李子印(1978— ),博士,副教授,硕士生导师,主要研究方向为图像处理、模式识别、视频压缩与通信等;
朱明凌(1989— ),硕士生,主研图像处理、视频压缩与通信。
责任编辑:闫雯雯
Mean-shift Tracking Algorithm Based Block
CHEN Zhu, LI Ziyin, ZHU Mingling
(College of Optical and Electronic Technology, China Jiliang University, Hangzhou 310018, China)
The mean-shift tracking algorithm based on block is proposed to solve the problem that tracking performance of traditional mean-shift algorithm decline under the occlusion and variation of target. Firstly, the target is divided into some similarly sized blocks which are tracked unobstructed part of target by traditional Mean-shift algorithm. Secondly, the effectiveness of target blocks are estimated by tracking detector and the invalid blocks are screened from the target, so the problem that the reduction of tracking performance which is caused by target blocks is solved. Thirdly, much more spatial information can be detected by normalized cross correlation detector and neighborhood homogeneity detector, so the limitation of mean-shift algorithm is made up and the robustness of tracking is increased. Experiment results indicate that the proposed algorithm can track under the occlusion and variation of target efficiently and accurately.
target tracking; target occlusion; variation of target; target blocked; Mean-shift tracking algorithm
国家自然科学基金项目(61007012);国家科技支撑计划项目(2012BAF07B05-3)
TN911.73
A
10.16280/j.videoe.2015.20.002
2015-04-08
【本文献信息】陈柱,李子印,朱明凌.基于块的Mean-shift跟踪算法[J].电视技术,2015,39(20).

