基于DWT-DFT和SVD域的盲水印算法
黄福莹,覃团发,陈 华
(广西大学 计算机与电子信息学院,广西 南宁 530004)
基于DWT-DFT和SVD域的盲水印算法
黄福莹,覃团发,陈 华
(广西大学 计算机与电子信息学院,广西 南宁 530004)
提出了一种基于离散小波变换、离散傅里叶变换和奇异值分解相结合的盲水印算法。该算法对原始图像进行一级离散小波变换后选择低频子带图像作分块离散傅里叶变换,然后对分块离散傅里叶变换的幅度谱进行奇异值分解,选择最大奇异值并采用量化嵌入方法实现水印的嵌入和盲提取。为了提高算法对旋转攻击的鲁棒性,采用基于Radon变换的检测算法对待检测图像进行旋转校正。实验结果表明,该算法对一些常规攻击和几何攻击都具有较强的鲁棒性。
离散小波变换; 离散傅里叶变换;奇异值分解;盲水印;鲁棒性
奇异值分解(SVD)是一种矩阵变换,对数字图像进行SVD具有一些显著特性[1],Zhou等人[2]证明了数字图像的奇异值对转置、镜像、旋转、放大、平移等几何失真具有不变性。基于SVD的水印算法对抵抗几何攻击具有一定的鲁棒性。现有水印算法中单一基于SVD的水印算法不多,多数情况是SVD与其他变换结合起来进行水印研究。胡娟等人[3]提出一种结合DWT和SVD的水印算法,解决了水印嵌入强度和图像质量的关系问题,但该算法由于需要进行分块DWT耗时较长。袁修贵等人[4]提出一种结合DWT-DCT和SVD的鲁棒水印算法,该算法提出了小波分解层次准则和水印相互嵌入准则,使得水印嵌入具有适应性。与大多数水印算法将水印嵌入到SVD的最大奇异值或奇异值不同,胡青等[5]将水印嵌入到SVD分解得到的奇异向量当中,通过正交矩阵向量系数间的制约关系调整其他系数值。叶天语[6]提出一种DWT-SVD域全盲水印算法,该算法通过自嵌入技术和盲提取认证水印序列达到全盲检测。褚静等人[7]提出一种DWT和SVD相结合的彩色图像水印算法,但水印检测需要原始图像,是一种非盲水印算法。
本文利用数字图像的DWT具有能量主要集中在低频部分的特点和DFT变换具有幅度谱的平移不变性的特点,结合SVD奇异值稳定的特点,提出一种基于DWT-DFT和SVD的盲水印算法。
1 基于DWT-DFT和SVD域的盲水印算法
1.1 Logistic混沌映射和Arnold置乱变换
本文采用Logistic混沌映射和Arnold置乱变换双重加密方法对水印在嵌入之前进行预处理。
Logistic映射所描述的是一个简单动力系统,其定义为
Xn+1=uXn(1-Xn)
(1)
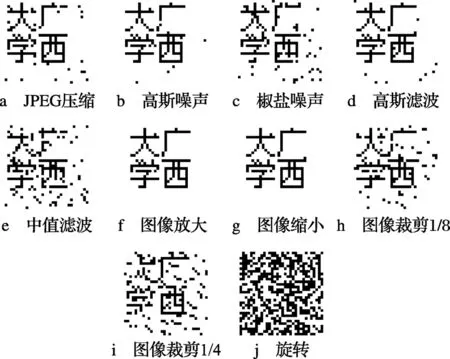
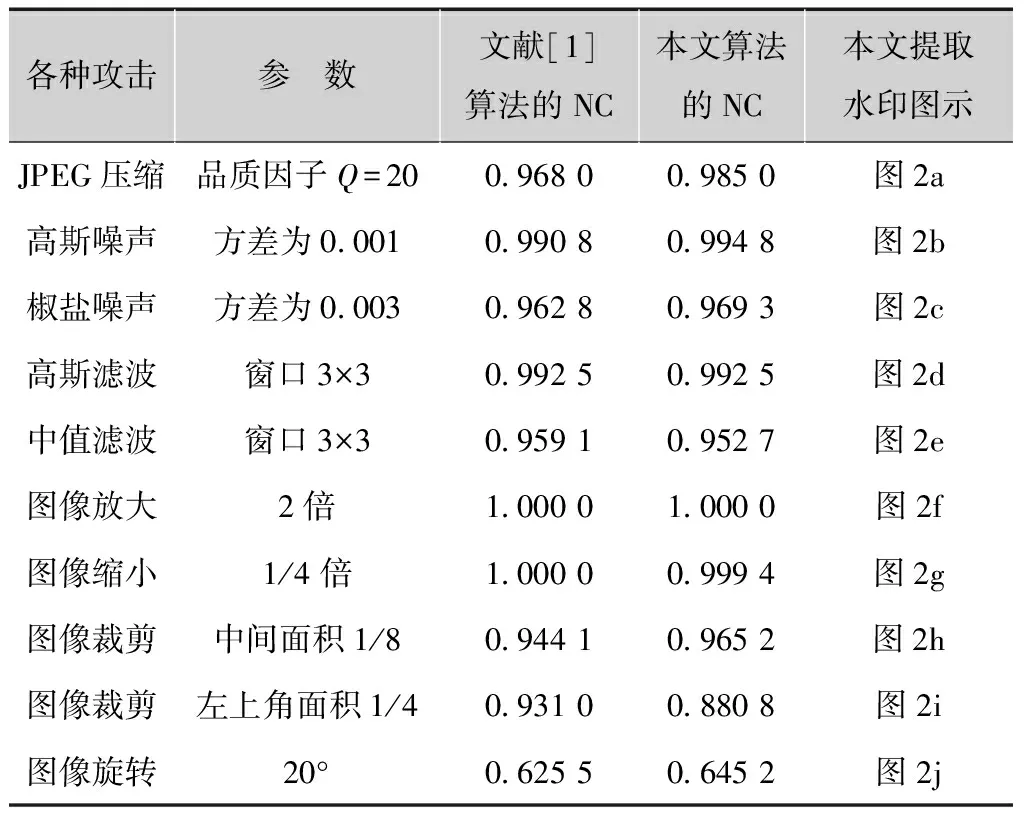
式中:Xn∈(0,1),当3.569 945 6 采用Arnold置乱变换可以减少像素间的相关性。设原始水印的大小为M×M,则水印的Arnold置乱变换的公式为 (2) 式中:xi和yi分别表示Arnold置乱变换之前像素的横坐标和纵坐标;xi+1和yi+1分别表示置乱变换之后后像素的横坐标和纵坐标。Arnold变换具有周期性,设其周期为T,则原始水印进行n(0≤n≤T)次Arnold变换后得到一个混乱的图像,再经过T-n次Arnold变换就恢复到原始水印。 本文水印预处理的方法是:先用Logistic混沌映射产生混沌序列,然后用混沌序列与二值化的水印信息进行逻辑异或运算,最后将异或结果进行Arnold置乱变换得到所要嵌入的水印信息。 1.2 DWT,DFT和SVD域 1.2.1 离散小波变换DWT 小波变换的基本思想是对信号进行细致的多分辨率分解。原始图像经过一级DWT后,分解成4个1/4大小的子带图像:LL1,HL1,LH1和HH1。子带图像LL1集中了原始图像的主要能量,其抗外在干扰的稳定性较好;而子带图像HL1,LH1和HH1保持了原始图像的边缘细节特征,易受外界因素影响,其稳定性较差。子带图像LL1是水印信息嵌入的理想区域,但该区域也是人眼视觉比较敏感的区域,如果直接在该区域嵌入水印信息,容易造成图像质量的明显下降。所以有必要对LL1进一步分解,本文采用的是DFT。 1.2.2 离散傅里叶变换DFT 设图像f(x,y)的大小为M×N,则其二维的DFT为 (3) 式中:u=1,2,…,M;v=1,2,…,N。 DFT的反变换为 (4) 其中,x=1,2,…,M;y=1,2,…,N。 由于数字图像的二维DFT变换的幅度谱具有平移不变性,本文选择DFT变换的幅度谱作为水印的嵌入区域。 1.2.3 奇异值分解SVD 图像DFT的幅度谱需要进行SVD分解后才嵌入水印,SVD的基本原理如下: 设A∈RM×N表示一个图像矩阵,R表示实数域,A的大小为M×N,则A的SVD可表示为 A=UΣVT (5) 其中,U∈RM×N,V∈RM×N是正交矩阵,Σ∈RM×N是一个非对角线上的元素都是0的矩阵,其对角线上的元素满足 λ1≥λ2≥…λr>λr+1=…=λM=0 (6) 其中,r是A的秩,λi是A的奇异值。 数字图像的第一个奇异值比其他奇异值要大得多,这对水印的嵌入非常有利,本文选择在分块SVD的最大奇异值中嵌入水印。 1.3 水印量化嵌入 为了实现盲水印检测,本文采用水印的量化嵌入方法。其主要思想是根据水印信息位的不同将待被嵌入水印的载体数据量化到不同的量化区间,在提取水印时根据所属的量化区间来识别水印信息位。 本文参照文献[3]的水印量化嵌入方法,设w为水印信息位,S为分块的最大奇异值,Q为量化区间。 (7) (8) 式中:mod(S,Q)表示求S对Q的余数。 1.4 基于Radon变换的检测算法 Radon变换检测算法的主要思路是[8]: 1)对原始图像作角度为0°的Radon变换,得到参照向量R0。 2)对待检测的含水印图像进行一组投影角从0°~359°(步长为1°)的Radon变换,得到360个检测向量R(θ),θ∈[0,1,2,…,359]。 3)计算每一个R(θ)与R0的相关系数NCR(i) i∈[0,1,2,…,359] (9) 1.5 水印嵌入和提取算法 1.5.1 水印嵌入 水印嵌入步骤如下: 1)由Logistic混沌映射产生混沌序列为L,设原始水印W大小为Mw×Nw,二值化后的W与L进行异或运算,经过Arnold置乱变换变成一维向量watermark,watermark就是待嵌入的水印信息。保存相关密钥。 2)设原始图像I大小为M×N,进行一级DWT,选择低频子带图像LL1。对LL1进行分块大小为(M/2)×(N/2)/(Mw×Nw)的DFT,取其幅频值A。 3)用式(5)对幅频值A进行SVD得到A=UΣVT,对角矩阵Σ中的第一个元素Σ(1,1)就是最大奇异值。 4)根据式(7)和式(8),用watermark对Σ(1,1)进行水印量化嵌入。 6)依次进行SVD逆变换,DFT逆变换和DWT逆变换,得到含水印图像I*。 1.5.2 水印提取 水印提取过程如下: 1)对I*进行一级DWT,选择低频子带图像LL1*进行分块DFT,取幅频值A*。 2)对幅频值A*进行SVD,选择最大奇异值S*。 3)根据式(10)进行水印提取 (10) 其中,Q为量化区间。 4)根据密钥,对watermark*进行Arnold反置乱变换,结合Logistic混沌序列,经过异或运算得到提取出来的水印W*。 5)计算W*与W的归一化相关系数NC。NC定义为 (11) 由于水印提取过程不需要原始图像和原始水印参加,因此本文算法是盲水印算法。 仿真实验以一幅32×32的二值图像为水印,以256×256灰度图像Lena作为原始图像进行水印嵌入,量化步长Q=320。图1为原始图像和原始水印,图2为含水印图像和提取水印。在不受任何攻击的情况下,峰值信噪比PSNR=39,说明其感知性没有明显变化,归一化相关系数NC=1,表明提取出来的水印和原始水印几乎没有任何改变。 图1 原始图像和原始水印 图2 含水印图像和提取水印 图3给出了含水印图像经过各种攻击后提取出来的水印。 图3 各种攻击提取出来的水印 为了表明本文所提出算法的优越性,在同等实验条件下,对本文算法与文献[3]的算法分别进行水印攻击实验,在嵌入水印之后未遭受任何攻击之前两种算法的PSNR均为39,在遭受各种攻击之后两者的归一化相关系数NC值如表1所示。 表1 含水印图像遭受攻击实验测试结果 各种攻击参 数文献[1]算法的NC本文算法的NC本文提取水印图示JPEG压缩品质因子Q=200968009850图2a高斯噪声方差为00010990809948图2b椒盐噪声方差为00030962809693图2c高斯滤波窗口3×30992509925图2d中值滤波窗口3×30959109527图2e图像放大2倍1000010000图2f图像缩小1/4倍1000009994图2g图像裁剪中间面积1/80944109652图2h图像裁剪左上角面积1/40931008808图2i图像旋转20°0625506452图2j 从表1可以看出,本文所提出的水印算法在JPEG压缩和图像裁剪两种攻击上获得比文献[3]更强的鲁棒性,对其他攻击这两种算法的鲁棒性差不多,但这两种算法对图像旋转攻击的鲁棒性都比较差。为了提高水印算法在图像旋转上的鲁棒性,本文采用Radon变换旋转检测算法取得很好的效果,实验结果如表2所示。 表2 Radon变换检测算法对旋转攻击的实验NC值 算法旋转角度1°5°10°20°50°100°200°300°不用Radon变换检测算法0761306664067020645206509062570639906664使用Radon变换检测算法0956209628094670935809218094670935809212 本文提出了一种基于DWT-DFT-SVD的盲水印算法。水印嵌入之前先进行Logistic混沌映射和Arnold置乱变换双重加密预处理过程,增强了水印的安全性。水印提取过程不需要原始图像和原始水印参与,是典型的盲水印算法。通过实验与文献[3]的算法相比较,本文所提出的水印算法在抵抗JPEG压缩、图像裁剪和图像旋转等攻击具有更强的鲁棒性。 [1] 王慧琴,王嘉路,王可,等﹒一种奇异值分解数字水印算法的研究[J].工程图学学报,2011(5):30-34﹒ [2] ZHOU B,CHEN J. A geometric distortion resilient image watermarking algorithm based on SVD[J]. Image and Graphics, 2004, 9(4):506-512. [3] 胡娟,杨格兰,严权锋. 结合DWT和SVD的鲁棒盲水印算法[J].工程图学学报,2008(4):107-110. [4] 袁修贵,周振.一种新的基于DWT、DCT和SVD的鲁棒水印算法[J].计算机工程与科学,2011,33(1):112-115. [5] 胡青,龙冬阳.基于DWT-SVD的奇异向量量化水印算法[J].计算机科学,2011,38(11):30-33. [6] 叶天语. DWT-SVD域全盲自嵌入鲁棒量化水印算法[J].中国图象图形学报,2012,17(6):644-650. [7] 褚静,徐安成,张美凤.DWT和SVD相融合的彩色图像水印算法[J].电视技术,2013,37(17):29-32. [8] FANG Xiaopeng,PENG Bo.Detection method of digital watermark about anti-attacking rotation based on radon[J].Computer Engineering and Design,2008(29):2069-2073. 黄福莹(1972— ),硕士,讲师,主研数字图像处理; 覃团发(1966— ),博士,教授,主要研究方向为多媒体通信; 陈 华(1958— ),博士,教授,主要研究方向为光电成像技术、数字图像处理。 责任编辑:闫雯雯 Blind Watermarking Algorithm Based on DWT-DFT and SVD Domain HUANG Fuying, QIN Tuanfa, CHEN Hua (School of Computer,Electronics and Information, Guangxi University, Nanning 530004,China) A blind watermarking algorithm is proposed in combination of discrete wavelet transform(DWT),discrete fourier transform(DFT) and singular value decomposition(SVD) domain. Firstly, a original image is conducted with one-level DWT and its low frequency wavelet band is split into non-overlapping blocks.Then each block is conducted with DFT and its amplitude is conducted with SVD. At last,the watermarking is embedded and extracted blindly with a quantization method in the biggest singular value of SVD.To improve the robustness to rotation attack, a detection algorithm based on Radon transform is adopted to correct the image to be detected. Experimental results show that the proposed algorithm has strong robustness to some common attacks and geometric distortion. DWT;DFT;SVD;blind watermarking; robustness 国家自然科学基金项目(61164019) TN911.73;TP391.4 A 10.16280/j.videoe.2015.20.003 2015-03-24 【本文献信息】黄福莹,覃团发,陈华.基于DWT-DFT和SVD域的盲水印算法[J].电视技术,2015,39(20).
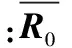
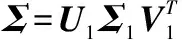
2 实验结果及分析



3 小结

