纵横交错八方联系——例谈高考对线性规划的考查

☉湖南省衡阳县职业中专 文自林

纵横交错八方联系
——例谈高考对线性规划的考查

☉湖南省衡阳县职业中专 文自林

线性规划在近几年高考中备受青睐，但是在高考中多以容易题出现，只要我们对该类问题加以总结，相信这类问题就容易解决.笔者经过多年的教学实践，归纳了线性规划的几种考查方式，欢迎同行批评指正.

一、考查线性目标函数的最值或值域

已知线性约束条件，求目标函数的最值或值域问题，在高考中是最基本的考查题型，一般分为四类：第一类是求线性目标函数的最值或值域；第二类是可转化为求可行域内一点到一定点的距离或距离的平方；第三类是可转化为可行域内一点与一定点连线的斜率；第四类是可转化为可行域内一点到一条定直线的距离.根据线性约束条件求线性目标函数的最值问题是标准的线性规划问题，在高考中是最常见的题型之一.

1.线性约束条件下，线性目标函数的最值

已知目标函数为z=ax+by（a＞0，b＞0），求z的最值.

解决策略：将z=ax+by转化为再通过平移直线在可行域中找使得直线在y轴上的截距取得最大值（或最小值）的点的坐标（x，y），即得线性规划的最优解.此时，直线在y轴上的截距取得最大值（或最小值）点的坐标（x，y）是z取得最大值（或最小值）时的最优解，两者恰好一致.

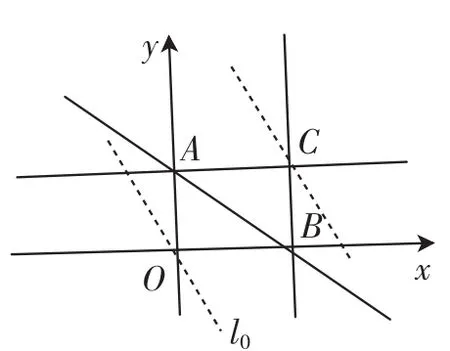
图1

解析：由z=2x+y，得y= -2x+z.如图1，当直线l0：y= -2x平移至经过点C（2，1）时，直线在y轴上的截距最大.所以，最优解为C（2，1），故zmax= 2×2+1=5.

点评：把线性目标函数转化为一族平行直线是图解法的核心，这种转化就是线性规划问题转化为一族平行直线与平面区域有交点时，直线在y轴上截距的最大值与最小值，此时要特别注意直线斜率的正负.

2.线性约束条件下，非线性目标函数的最值

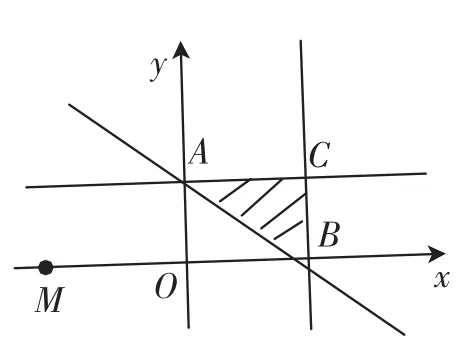
图2

图3

解析：由z=（x+2）2+y2，得求z的最小值转化为求可行域内的点P（x，y）与定点M（-2，0）两点间距离的最小值的平方，如图3.所以，当点P（x，y）取A（0，1）时

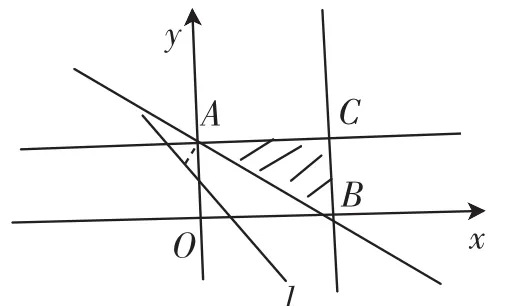
图4

3.非线性约束条件下，线性目标函数的最值

此类问题关键是要能弄清楚非线性约束条件在平面区域内所表示的图形，解法与第一大类型问题一致.

例5已知x，y满足x2+y2=1，求z=2x+y的最大值和最小值.

解析：由z=2x+y，得y=-2x+z.又x2+y2=1表示圆，如图5，当直线l0：y=-2x平移至经过点C时，直线在y轴上的截距最大.所以如图5，当直线l0：y=-2x平移至经过点A时，直线在y轴上的截距最小.所以

用规划思想求目标函数的最值，关键是要弄清目标函数的几何意义及掌握约束条件所表示的几何图形.

图5

二、考查可行域的面积

这一类问题通常是先画出不等式组所表示的平面区域，根据平面区域的形状来求可行域的面积，若可行域是三角形，可根据三角形面积公式求解，若可行域是四边形或更复杂的图形，除可用面积公式求解外，也可用分割法求图形面积.

解析：画出不等式组表示的平面区域，它是由直线x+y=0，x-y+4=0和x=1围成的三角形区域，三角形的三个顶点坐标为（-2，2）、（1，-1）、（1，5），可求得三角形的面积为9.

三、考查参数的值或取值范围

已知目标函数的最优解求解参数范围，这种逆向考查线性规划问题是近几年高考的热点题型，旨在考查学生的逆向思维能力.在所考查的试题中，参数的位置有的在线性约束条件中，也有的在目标函数中.

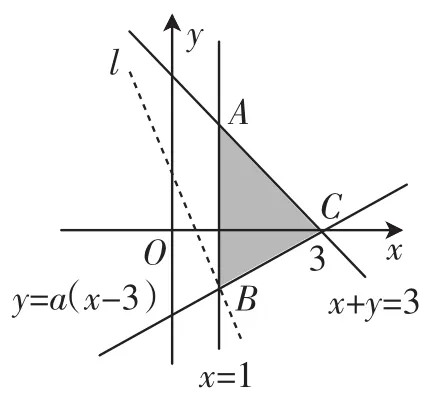
图6

解析：由已知约束条件，作出可行域，如图6中△ABC内部及边界部分，由目标函数z=2x+y的几何意义为直线l：y=-2x+z在y轴上的截距知，当直线l过可行域内的点B（1，-2a）时，目标函数z=2x+ y的最小值为1，则2-2a=1，即故选B.

四、线性规划知识的交汇问题

将线性规划与其他数学知识进行交汇命题，在近几年的高考试题中，成为考查线性规划问题的热点.线性规划可以与函数和导数、集合、数列、不等式、向量、概率、解析几何等数学知识进行综合，重点考查函数思想、数形结合思想、转化与化归思想，考查分析问题、解决问题和综合运用数学知识的能力.解决线性规划与其他数学知识的交汇问题，不仅要掌握解决线性规划问题的基本方法，还要具有将与线性规划相交汇的知识进行转化的能力.

1.与函数或导数知识相结合

线性规划与函数或导数知识相结合，近几年的高考试题出现的题目比较多.与函数问题相结合，主要是在线性约束条件下，曲线经过可行域的何处时有适合题意的最优解；与导数问题相结合，主要是先求出曲线在某点处的切线，再转化为线性规划问题.

例8抛物线y=x2在x=1处的切线与两坐标轴围成的三角形区域为D（包含三角形内部和边界）.若点P（x，y）是区域D内的任意一点，则x+2y的取值范围是________.

解析：因为y′=2x，所以当x=1时，y=1，y′=2，则过点（1，1）的切线方程为y=2x-1，所以切线与两坐标轴围成的三角形区域端点为（0，0）、（0，-1），所以x+2y在点处取最大值在点（0，-1）处取最小值-2，即x+2y的取值范围为

2.与向量知识相结合

线性规划与向量知识相结合，在近几年的高考中出现的题目也比较多，题型主要是在线性规划背景下加入向量问题（由向量条件得到目标函数），或是在向量背景下加入线性规划问题，也有的是由向量条件得到线性约束条件从而转化为线性规划问题.解决这类问题的关键是准确地利用向量知识将问题转化为线性规划问题，结合线性规划问题的类型进行求解.

例9已知O是坐标原点，点A（-1，1），若点M（x，y）是平面区域上的一个动点，则的取值范围是（）.

A.［-1，0］B.［0，1］C.［0，2］D.［-1，2］

3.与概率（几何概型）知识相结合

线性规划与概率知识相结合，主要是借助于线性规划的可行域，考查几何概型的概率求解问题，其中线性约束条件所满足可行域的面积对应于几何概型问题中的几何测度.

4.与多个知识点相综合

这类问题通常是在选择题或填空题的压轴题位置，试题将线性规划问题与多个知识点相综合，具有相当高的难度，试题难在解题方法的创新上和转化与化归的能力上.这类问题的解题关键是要读懂题目，根据条件的结构特征进行适当的变形，利用适当的数学方法（如换元法等）转化为线性规划问题.

例11已知正数a，b，c满足：5c-3a≤b≤4c-a， clnb≥a+clnc，则的取值范围是__________.

解析：由5c-3a≤b≤4c-a及clnb≥a+clnc，得：则本题可化为下列问题：已知x>0，y>0，且的取值范围.作出不等式组表示的平面区域，如图则当直线y=kx与曲线y=ex相切时，k取最小值e，此时切点坐标为（1，e）；当直线y=kx过直线3x+ y=5与x+y=4的交点）时，k取最大值7，从而的取值范围为［e，7］，即的取值范围是［e，7］.

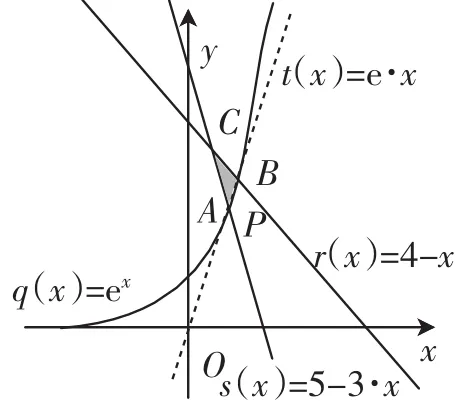
图7

当然，线性规划与其他知识点的交汇问题远不止这些，例如线性规划与数列、解析几何等数学知识的交汇等，但是解决问题的一般思路和方法是类似的，关键是要掌握线性规划基本问题的解法，合理地将问题中所涉及的知识点进行转化.对一些较为复杂的问题，可从问题结构形式入手，将问题转化为熟悉的知识进行解决.线性规划思想在解决牵涉各类不同问题的题目中，有很重要的应用价值，巧用线性规划知识，可使问题变得更清晰，过程更简捷.