教育对经济增长作用的省际面板数据比较分析

刘深

摘 要：教育与经济是互动发展的内生系统，教育作为培育和增加人力资本的根本途径，在推动经济增长方面发挥着巨大的作用。为研究教育与地区经济发展间互动关系，文章借鉴内生经济增长理论的相关论述，在Cobb-Douglas生产函数的逻辑架构上设定模型基本形式，并在此条件下，基于2006-2012年的省际面板数据，建立关于教育要素的变系数面板数据模型来对这一问题进行实证分析，进而比较31个省（市、自治区）教育对经济带动作用的地区差异。实证结果表明，教育发展对地区经济增长具有显著的推动作用，而且这一作用呈现出较为明显的地域性差异特征。

关键词：教育;经济增长;省际;面板数据;人力资本

一、引言

理论和实证分析表明，教育与经济是互动发展的内生系统，教育作为培育和增加人力资本的根本途径，在推动经济增长方面发挥着巨大的作用。为了准确认识教育对经济增长的作用，半个世纪以来，国内外学者积极运用定量经济学方法对教育与经济增长的关联关系作实证分析。其中，最经典的成果当属美国经济学家舒尔茨（1961）提出人力资本概念，他以余值分析法，论证了美国1929-1957年间，教育程度的提高对国民收入增长的贡献。丹尼森（1962）也提出了经济增长因素分析法，他通过分解教育量指数，最完整地分析了经济增长源泉和教育对经济增长的贡献。而后教育经济学者又提出了多种代表性模型，如罗默的知识积累模型、卢卡斯的人力资本模型、格拉斯生产函数模型等，学者们根据不同理解将这些模型应用于研究教育与经济增长关系的实证分析中[1]。近期以来，国内越来越多的学者采用了内生经济增长模型，崔玉平（2002）运用Cobb-Douglas生产函数计算出1982-1990年教育对国民收入的贡献率为8.84%[2];张开洪（2008）引入教育综合指数，使生产函数模型变形后，分析出中部6省高等教育对经济发展的贡献率在2%左右[3];杨天平、刘召鑫（2014）将生产函数模型，结合教育综合指数法，对中国高等教育对经济增长的贡献率进行测算，2001-2011年间，高等教育贡献率为3.62%[4]。从研究方法上看，国内学者们应用生产函数测算，利用协整检验与格兰杰因果关系检验等国外最新发展的一些模型来进行研究，以期真正揭示出教育与经济增长的定量关系。

针对前人成果中定量分析有所欠缺，或者对特定区域的教育与经济非均衡状况研究不足的问题，本文拟运用内生增长理论和Cobb-Douglas生产函数模型，构建教育与经济增长的关联模型，利用2006-2012年31个省（市、自治区）的面板数据进行实证检验，探讨教育对经济增长相互推动的作用关系，再按东中西三大地区比较分析地区差异，最后形成结论意见。

二、分析架构与模型

（一）包含教育要素的C-D生产函数

Cobb-Douglas生产函数是主流经济增长理论背景下的基本增长函数，由Paul H.Douglas和Charles Cobb在研究美国制造业数据时共同提出，该函数具有以下形式：

Yield=A·Laborα·Capitalβ

表示产出依赖劳动力和资本的投入，指数α和β分别表示产出对劳动力和资本投入的弹性系数，一般而言，α+β=1表示规模报酬不变，α+β>1表示规模报酬递增，α+β<1表示规模稿酬递减。参数A在各类主流经济增长理论中，均被视为生产过程中的技术要素，其对数形式即为全要素生产率。

内生增长理论认为增长模型中包含两种资本，一种是累积的实际资本，一种是提高投入要素使用效率或是提高生产率的人力资本（Lucas，1988）;人力资本的形成主要来源于教育与干中学（learning by doing），后者即是指在一定的技术背景下，劳动者在生产产品或提供服务过程中积累经验，对自身专业技能不断熟练和提升的过程[5]。

劳动者干中学的情况通常无法直接用可观测指标衡量，而且，由于干中学需要一定的技术环境作为前提，就业者干中学的知识积累能力和效率也与其受教育程度存在关联关系。因而，在本文的实证分析中，选择将教育视为人力资本形成的主要因素。在这一假设前提下，将人力资本要素作为劳动要素投入引入传统的Cobb-Douglas生产函数，则可得到如下式子：

（1）

由式（1）可以看出，经济体的产出不仅依赖资本要素积累，还与每位劳动者的素质存在关联;换言之，教育通过提高劳动者素质，增加地区人力资本储备，进而促进地区经济增长。

（二）面板数据模型

面板数据是同时包含特定时点上多个被观测个体的数据，及各个被观测个体在时间轴上的动态变化情况的数据集。相对于截面数据和时间序列数据而言，面板数据在模型拟合方面包含更多可利用的个体信息，由此也可得到更为灵活、精度更高的估计结果。

面板数据模型大致包含混合（pooled）模型、固定效应（fixed effect）模型和随机效应（random effect）模型三种形式，其基本形式如下：

Yit = α + β Xit + εit     （2）

其中，Yit 是个体i在t时刻的因变量观测值，Xit 是自变量观测矩阵，εit是观测中存在的随机扰动因素，α和β是模型参数。对于混合模型，截距α和斜率β不随时间和个体的不同而改变，意味着不同个体服从同一较为平稳的分布特征;如果观测个体来源于不同整体，其特征和表现存在彼此间差异，则需要根据不同假设条件，将模型（2）设定为固定效应模型或随机效应模型。对于固定效应模型和随机效应模型的确定，一般根据Hausman检验的结果，或者根据实际研究的问题背景和样本性质进行选择（Hsiao，2003）。此外，还可以设定因个体差异导致斜率β不同的变系数模型[6]。

本文将在生产函数式（1）的架构下，选取适当面板数据模型，探索全国31个省（市、自治区）面板数据背后教育与经济增长的作用关系，进行省际比较分析。endprint

三、实证分析

（一）省际面板数据描述与检验

本文用于分析的数据样本为全国31个省（市、自治区）2006-2012年的经济与教育数据，主要来源于国家统计局的分省年度数据库及各年度的《中国人口和就业统计年鉴》。其中，地区生产总值根据各地的平减指数调整为2006年不变价水平;固定资产投资经过价格指数调整后，按照0.05的折旧率计算各年份的资本存量;就业人员的平均受教育年限根据就业人员受教育程度构成分布进行计算。

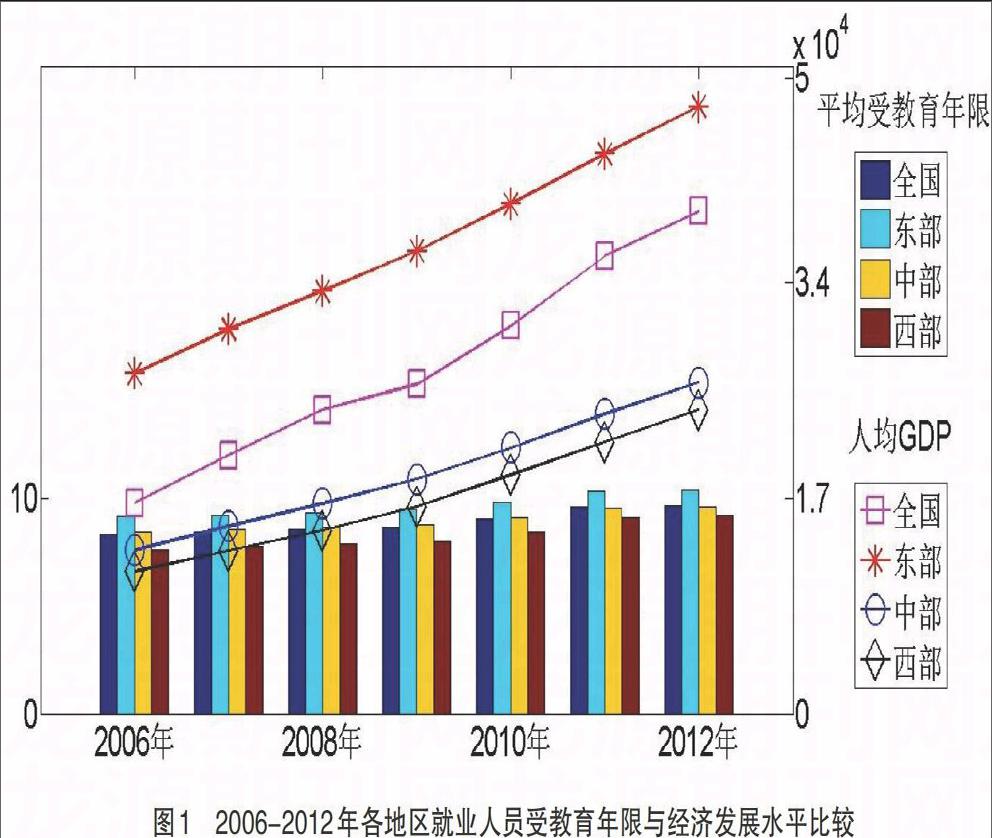
图1显示的是各地区就业人员平均受教育程度与人均地区生产总值的变动情况，可以看出，就业者受教育程度高于全国平均水平的东部地区具备相对较高的经济发展水平，而对于教育水平相对落后的中部和西部地区，其经济发展状况均落后于全国平均水平。此外，地区的教育水平也与经济发展水平呈现出了相一致的发展趋势，但仍相对落后于经济发展的势头：2006-2012年间，东部地区的人均GDP年均增长10.13%，年均教育年限年均提高2.12%;中部地区人均GDP年均增长12.43%，而教育水平年均增长率为2.15%;西部地区的两项指标增长率相对较高，分别为13.47%和3.18%。下文也将通过面板数据模型的拟合，来对教育与经济发展间的动态关系和区域差别做进一步的阐述。

在建立模型前，需要对相应变量的观测数据进行检验。在上述讨论的基础下，考虑引入各省地区生产总值（GDP）作为对经济发展情况的度量，资本存量（Cap）数据作为资本投入的反映，而人力资本（Hcap）则用各省的就业人员平均受教育年限与当地就业人口的乘积进行计算，该指标同时也能反映出地方教育的发展水平。根据式（1），设定这三项指标有以下关系式

log（GDP）=β0+β1log（Cap）+β2log（Hcap）+εit （3）

对对数变换后的数据进行单位根与协整检验，计算过程在Eviews中完成，结果如表1所示。

表1 变量单位根与协整检验结果

LLC单位根检验是一种常用的面板数据单位根检验方法，由于运用了面板数据样本的信息，具有较好的检验优势。在合理的模型设定下，该检验结果显示各变量均显著为1阶单整序列，这为直接将这三项变量引入模型进行协整检验提供了合理性。

协整关系是判断变量间是否存在长期稳定关系的依据，目前学者已经提出了多种统计工具对面板数据进行协整检验，本文主要使用了Eviews中的Kao检验和Pedroni检验。其中，Kao检验是基于残差的一种检验方式，包含DF和ADF两种形式，后者包含残差差分的滞后项而前者不包含，本文所使用的是后者;在Kao检验下，ADF-t统计量显著支持三变量存在协整关系的假设。Eviews输出的Pedroni检验结果可以分为两类，一类是假设不同截面具有相同的自回归系数的Panel统计量，一类是假设不同截面具有不同的自回归系数的Group统计量，加之不同的检验方式总共有七项统计量。在这七项Pedroni检验统计量中，除了Panel中的v和rho检验及Group中的rho检验不显著外，Panel的和Group的PP和ADF均显著支持对数GDP、对数资本存量和对数人力资本间显著存在协整关系。结合Kao检验和Pedroni检验结果可以认为对数GDP、对数资本存量和对数人力资本存在协整关系，可以同时用这三项指标建立面板数据模型进行分析。

（二）教育对经济作用的地区差异比较

在式（3）的设定关系下，备选的面板数据模型可以是混合模型，固定效应模型，随机效应模型，以及为了反映各地教育对经济增长作用所设定的教育要素变斜率模型和教育要素变斜率固定效应模型，总共五种模型形式。

通过Hausman检验比较固定效应与随机效应模型，用F检验比较混合、固定效应和变系数的固定效应模型，再用似然比检验比较教育要素的变斜率及固定效应和教育要素的变斜率模型;经过一系列比较，最终选择教育要素的变斜率模型对31个省（市、自治区）的面板数据进行分析。估计结果（如表2）显示，变系数模型对样本数据有不错的拟合效果：各项系数检验结果均显著，F统计量显示模型整体也具有显著的统计意义，能够解释因变量数据中99.90%的方差变动信息。

在本文变系数模型的设定下，系数β2表示不同地区就业人员整体受教育程度的提升对当地经济水平增长的推动能力。根据表2显示的模型拟合结果，就业者整体受教育程度对经济增长的贡献作用最为突出的是广东省，为0.341，江苏、山东、浙江、河北、河南均在0.300以上。从东、中、西三个地区省份该系数的均值来看，东部地区为0.297，中部地区为0.282，而西部地区仅为0.240，明显低于东部和中部的水平。

从另一侧面可看出，在本文所选取的样本时期内，资本要素仍在各地区经济运行过程中充当重要推动力，显示出资本存量每增加一个百分点，平均会促进地区生产总值0.545%的增长。全国31个省（市、自治区）中人力资本系数β2在0.300以上的仅有6个省份，这证实了目前我国经济增长仍以投资拉动型为主要特征的现状。

进一步分析教育对经济增长作用的地区差异，以下分别对东部、中部和西部地区的人力资本系数进行核密度函数估计，结果如图2所示。

由图2看出，教育较为发达的东部地区，其教育发展对经济增长的作用同样具有相对较高的水平，分布呈现出右偏特性，说明大部分东部省份集中在均值0.297及以上的位置，东部的11个省（市）中只有海南表现略显不足，该系数仅为0.230;中部地区则相对集中在0.25到0.30的区间段，呈现出关于均值0.282的对称分布;西部地区人力资本系数β2的分布较为分散，且该地区省份的教育对经济增长的推动作用普遍偏低，呈现出较为明显的左偏性质，只有四川、内蒙古和广西达到了中部地区均值以上的水平，三省（自治区）的该项数值分别为0.288、0.287和0.282。由此说明东部、中部和西部地区之间的发展差异，不仅表现在教育水平的差异，还表现在教育对经济增长作用程度的差异。endprint

四、结论性意见与建议

通过定量分析我国教育对经济增长的作用，得到如下几点结论性意见与建议：

（一）教育与经济增长之间存在长期相互作用关系

本文利用全国31个省（市、自治区）2006-2012年的经济与教育数据，通过建立包含教育要素的经济增长模型，对教育发展对经济增长的作用进行了实证分析。使用Eviews中的Kao检验和Pedroni检验的结果表明，经济与教育存在协整关系。说明我国教育与经济增长之间存在着互相促进关系，教育水平提升为经济增长提供动力，经济增长能够支撑和促进教育的发展，教育对于经济增长的作用比较明显。教育是支持经济长期增长的重要因素。未来我国仍需进一步统筹教育与经济协调发展。建议继续推动教育事业优先、全面发展。建立和完善多元化教育投入保障机制，加大公共教育投入，各级政府应巩固教育经费支出占GDP比例4%的成果，不断提高教育经费保障水平。鼓励社会资金以多种形式进入教育领域。

（二）人力资本是经济增长重要的内生变量

我国东、中、西部地区的人力资本系数β2反映了从业人员整体受教育水平对经济发展呈现出正向促进作用，证实了人力资源是地区经济增长的重要源泉之一。教育产出的重要目标就是培育和增加人力资本，事实上，教育导致知识的传播，使劳动者技术水平和生产效率提高，能够为经济可持续发展提供动力和支撑。因此，教育是人力资源开发的根本路径，人力资本通过教育对经济增长发生作用。今后我国仍需进一步优化人力资本配置。建议放大教育对人力资本开发的关键作用，创建有利于人力资本积累和提高的环境条件，使人力资本真正成为经济增长的核心动力。

（三）教育对经济增长的驱动能力相比资本存量要素仍显不足

根据模型拟合结果，资本存量的单位百分比增长对经济增长的带动作用平均约为0.545%，而就业者整体素质的相应系数的31省（市、自治区）平均值为0.271，仅为资本存量贡献的一半。这一方面反映我国经济对资本要素的依赖高于人力资本的现状;另一方面说明目前我国教育发展仍然不足，需要继续加大政府在教育领域的投入。建议通过深化教育改革和教育扩大开放，积极调整职业教育、高等教育结构，促使教育规模与经济发展、社会人才需求相适应，扩大人力资源储备规模。

（四）教育对经济增长的推动作用呈现地域性差异特征

从数据和模型估计结果可以看出，教育的地域差异不仅在于就业者总体受教育水平的区别，同时还表现在该指标对经济发展的推动作用上。东部地区的就业人员整体受教育水平相比中部和西部对经济发展有更高的推动作用，而西部地区的促进作用则相对偏弱。该问题主要在于西部地区教育发展基础较为薄弱;高等教育和职业教育与当地经济产业发展衔接不足;研发条件落后，无法留住高端技术人才;等等。建议促进区域、城乡教育均衡发展，完善中央教育经费转移支付制度，加强对欠发达地区、农村地区、薄弱学校和困难群体的扶持力度，实现优质教育资源普及共享;西部地区应科学设置与当地特色产业相配套的专业，大力提升当地教育的内涵发展水平;加强高等教育、职业教育与地区经济增长的适应性和匹配性，明显提高教育对经济社会发展的贡献作用。

参考文献：

[1]杨建芳，龚六堂，张庆华.人力资本形成及其对经济增长的影响——一个包含教育和健康投入的内生增长模型及其检验[J].管理世界，2006（5）：10-34.

[2]崔玉平.高等教育制度创新的经济学分析[M]，北京：北京师范大学出版社，2002：88-104.

[3]张开洪.中部六省高等教育对经济增长贡献率的比较研究[J].统计与决策，2008（17）：84-86.

[4]杨天平，刘召鑫.中国高等教育对经济增长贡献率的分析比较.高校教育管理[J]，2014（3）：7-16.

[5]Lucas.On the Mechanics of Economic Development[J].Journal of Monetary Economics. 1988（22）：3-42.

[6]Hsiao.Analysis of Panel Data[M].New York：Cambridge University Press，2003：27-46endprint