一种两阶段的航班延误模式提取方法
孟会芳,彭 怡(南京航空航天大学民航运输优化实验室,211100南京)
一种两阶段的航班延误模式提取方法
孟会芳,彭 怡
(南京航空航天大学民航运输优化实验室,211100南京)
针对民航运输系统日益严重的航班延误问题,提出一种两阶段的航班延误模式提取方法.该方法运用相空间重构理论和递归图方法,对航班延误率的混沌特性进行分析.然后,在获取延误率子序列的基础上,结合定量递归分析理论,采用K⁃means聚类技术提取航班延误模式,并对各种延误模式进行时变分析.实例验证表明,该方法不但能有效地提取航班延误模式,而且可以获取延误模式的时变特征,研究成果对机场和航空公司航班延误预测及预警提供了管理决策依据.
航班延误;相空间重构;混沌性;定量递归分析;延误模式;时变特征
航班延误是民航界亟待解决的重要问题,国内外专家学者对航班延误做过大量的分析研究.文献[1]设计了航班计划恢复决策支持系统,在航班已经发生延误的情况下,以延误航班和取消航班架次最少为目标,搜索所有可用飞机和机组资源,恢复被扰乱的航班计划;文献[2]以飞机和旅客的恢复成本、取消成本、延误成本最小化为目标函数,建立了飞机和旅客一体化恢复模型;文献[3]将风险比例模型运用到航班延误波及的研究中,从航班运行机制角度入手,对航班延误因素进行分析,指出过站时间、机型、行李货邮、维修计划、旅客和行李处理、天气是造成离港航班延误的主要因素;文献[4]建立了基于贝叶斯网络的航班延误因素分析模型,探究了不同因素对航班延误的影响程度;文献[5]通过对空中油耗可信度进行分析指出,采取降低巡航高度、修改最佳飞行高度及减小巡航速度等手段可以有效减少地面延误.这些研究成果主要集中在对航班延误原因的梳理和延误后的恢复机制方面,属于事后处理机制的范畴,是航班延误发生后的资源调整和控制,是被动的管理策略.当然,也有部分学者[6-7]提出对航班延误状态评估及延误预警的方案,但也都是主要研究一段时间内总的航班延误数量及延误等级或是以概率性事件预测延误的可能性,对航班延误发生之前的模式规律研究鲜有涉及.鉴于此,本文在上述研究的基础上,着力对航班延误模式进行分析.基于延误率的变化规律,运用非线性动力学理论构建了一种定性和定量相结合的航班延误模式提取方法.
该方法分为2个阶段,如图1所示.
1)定性分析.基于混沌理论对航班延误率的时间序列进行相空间重构,将重构后的相空间运用到递归图分析(recurrence plot,RP),验证航班延误率时间序列的混沌特性.
2)定量分析.在定性分析研究的基础上,结合CUSUM算法将时间序列划分为不等长的子序列,然后对每个子序列进行定量递归分析(recurrence quantification analysis,RQA),提取特征参数.运用K⁃means方法获取航班延误模式,对每种延误模式在一周内每一天的分布情况加以分析.
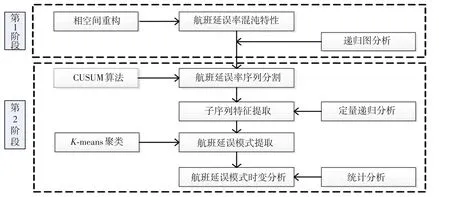
图1 航班延误模式提取方法技术路线
1 航班延误率时间序列混沌特性分析
时间序列的混沌特性分析都是在特定的相空间内进行的,因此,分析航班延误特征的第1步是进行有效的相空间重构,而递归图则直观地反映了系统的混沌特性.在航空运输系统中,航班延误是由多种原因(机场、航空公司、空管、天气等)造成的综合结果,而一般情况下研究人员关注的重点往往只是最终的延误水平.因此,本文一个最基本的想法是认为所有观察到的以及未被发现的影响因素造成的后果都可以通过最终延误水平这一变量反映出来,即选取平均航班延误率作为所要考察的时间序列.根据文献[8]的延迟嵌入定理可知,只要选取合适的延迟时间τ和嵌入维数m,将一维变量投影到高维空间,原系统暗含的动力特征将得以重现.假设原始平均航班延误率时间序列为X={xi,i=1,…,N},重构相空间后得到一个(N-(m-1)τ)×m的矩阵Y,其中Yi=(xi,xi-τ,…,xi-(m-1)τ),i=(m-1)τ+1,…,N.Yi为航空运输系统在i时刻的航班延误状态,是m维嵌入空间中的一个相点.
1.1 相关参数的确定
文献[9]中介绍了多种确定最优时间延迟τ和最佳嵌入维数m的方法,为了在Rm空间中充分刻画出原模型的性质,综合考虑各种方法的优缺点,本文采用文献[10-11]提出的平均互信息法确定最佳延迟时间τ,用Frase提出的虚假最近邻算法(FNN)确定嵌入维数m.
1.1.1 延迟时间τ的确定

式中:P(xi)、P(xi+τ)、P(xi,xi+τ)分别为概率;P(xi)、P(xi+τ)可以通过计算时间序列的直方图获得;P(xi,xi+τ)可以通过计算时间序列的二维直方图获得.选取I(τ)第1次达到局部极小值时的τ为最优延迟时间,因为此时观测时间序列具有最大的独立性和最小的冗余.
1.1.2 嵌入维数m的确定
虚假最近邻点是指当嵌入维数较小时吸引子在相空间中不能完全打开而投影到一起,但是原系统中这两点并不是真正的近邻点.判定虚假最近邻为

给定一个阈值R,若a(i,d)>R,则xNN(i)是x(i)的
1虚假最近邻点,R∈[10,50].当m增加到m+1维,虚假最近邻点的比例小于5%或者不再随着m的增加而减小时,可以认为混沌吸引子完全打开,此时的m就是最佳嵌入维数.
1.2 航班延误率时间序列递归图
文献[12]提出递归图(RP)的概念,旨在以图形的方式定性地展示动力系统的混沌性、非平稳性及周期性等递归特性.递归图的构建以相空间重构为基础的,利用相空间的点得到一个描述时间序列内部动力学特性的二维矩阵图,其实质则是由0和1组成的N阶方阵[12],如
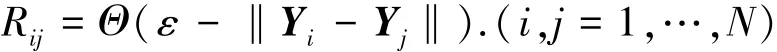
式中:ε为邻域半径,是一个预先给定的阀值,一般取时间序列标准差的15%,Θ(·)为Heavside函数,即

令dij=‖Yi-Yj‖,dij为状态向量Yi与Yj距离远近的度量.
在周期性时间序列中当i-j =nT(n=0,1,…,T)时,dij=0,而非周期性时间序列没有这样的性质.所以,为直观反映重构后所有状态向量两两之间的距离,规定当dij≤ε时认为两向量靠近,两相点递归,在点(i,j)处显示黑点,即j时刻相空间中的1点在i时刻返回到它所在的相空间邻域中;否则认为两向量相距较远,两相点非递归,在(i,j)处显示白点.也就是说在航班延误系统中,利用航班延误率构建递归图,比较重构后两相点Yi和Yj的距离,若dij大于规定值,则画一个黑点,表示i时刻与j时刻的状态具有递归性;否则画一个白点,表示i时刻与j时刻的状态相互独立,从而得到一个具有特定图样结构的矩阵图.若递归图中的颜色分布具有一定的规律性,说明航班延误系统中存在确定性成分,具有一定的混沌特性,该系统的可预测性强;否则该系统的随机性较强,难以预知.
2 航班延误模式提取
航班延误模式提取方法主要是根据航班延误率时间序列的变化特点,利用CUSUM算法分割子序列,运用RQA提取出各个子序列的特征参数作为K⁃means聚类的输入指标提取出典型的航班延误模式.
2.1 CUSUM算法分割航班延误率子序列
人为等时段划分序列间隔忽略了数据本身的变化特性,是一种生硬的分割方法.为了克服对序列波动过程和统计特征造成破坏,本文根据序列内部变化特性进行自然划分,通过对样本序列数据信息的积累,采用CUSUM算法对时间序列进行分割,将小的偏移放大,达到提高检测数据偏移灵敏度、探测数据序列发生改变的拐点的目的[13].算法步骤如下:
1)设置最小分割长度阈值λ,计算航班延误率时间序列均值x-;=+
2)计算各点航班延误率累计和SiSi-1(x,其中i=1,…,n,取初值S0=0;
4)对每个子序列基于拐点进行二分,反复进行步骤3);
5)当每个子序列的长度都小于λ时,算法停止.
2.2 基于RQA的航班延误率子序列特征参数提取
虽然RP可以直观地对系统进行定性分析,但是很多情况下人们希望对系统进行量化分析.为了更准确的描述和区分时间序列的内在规律,量化递归图的指标受到越来越多学者的重视.文献[14]提出利用递归度、确定性、最长对角线因子、递归熵、趋势5个指标量化递归图中的状态点和线段的分布.随后,文献[15]又引入了递归趋势、分歧度、分层度、平均对角线长度等量化指标,从而形成了系统的定量递归分析方法.不同的RQA指标描述了系统不同的动力学行为,反映了航班延误率的递归特性[16].考虑到航班延误的实际情况,本文选取5个常用的非线性指标量化参数.
1)递归率(RR).表示递归图中所有递归点(黑点)占全部点数的百分比,也就是当前状态递归和复显的可能性,递归率越大系统的周期性越强.
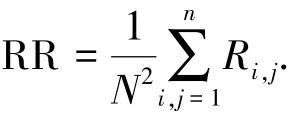
2)确定率(DET).表示所有与主对角线(45°)平行的线段上递归点占所有递归点的比值,是数据结构确定性的指标,值越大表明系统确定性越强.在周期性时间序列中,有序规则的线段递归点多,DET都大于0;而随机时间序列中,离散孤立的递归点多、对角线少,DET趋近于0.

式中:P(l)表示长度为l的对角线的分布概率,lmin一般取2或3.
3)递归熵(ENTR).刻画递归图中平行于主对角线的线段的Shannon熵,是数据结构复杂度的指标,值越大表明系统结构越复杂.

4)最长对角线因子(Lmax).平行于主对角线(不包括主对角线)的所有线段的最大值,表示数据序列非线性特征的指标,值越小非线性越强,混沌性越强越不平稳.

5)分层度(LAM).指组成规则线段(垂直/水平)的递归点的百分比,描述系统变化快慢,值越小变化越快.

式中:P(v)为长度为v的线段(水平/垂直)分布概率;vmin为最短线段长度,一般取2或3.
3 实例分析
本文实验数据来源于国内某大型枢纽机场航班实际生产运行数据,选取2013年11月4日至2013年11月10日一个典型周的数据,由于航班计划是以5 min为间隔制定的,所以数据统计间隔最小为5 min,分5、10、15 min记录航班延误率.
3.1 不同时间尺度的航班延误率时间序列相空间重构及RP分析
图2是利用平均互信息法和FNN方法得到的不同时间尺度的延迟时间和嵌入维数,从左到右依次是5、10、15 min.从图2中可以看出3个时间尺度的延迟时间分别在3、4、3处达到极小,即15、40、45 min,所以最优延迟时间为3、4、3;嵌入维数均在2时使虚假最近邻点趋于稳定,所以最佳嵌入维数均取2.

图2 不同统计时间尺度的延迟时间和嵌入维数
若系统内部隐含某种规律,那么在递归图中的具体表现形式就是图形内部线条呈现某种特定形状.图3是利用RQA的航班延误率子序列特征参数提取的方法构建的3种统计间隔的航班延误率时间序列递归图,从左到右依次是5、10、15 min,3幅图形均由特定结构的规则线段和黑点组成,可以看出第1幅图的黑色规则线条分布比较均匀,而第2、3幅图形中规则线条减少,具有随机特性的黑点增多,说明每种统计间隔的递归图都呈现出一定的规律性,并且随着统计时间间隔的增大规律性减小,也就是说采用较短的统计间隔能够减少延误率时间序列的随机性,增强周期性,因此以下分析均采用5 min统计间隔的航班延误率时间序列.

图3 不同统计时间尺度的航班延误率递归图
3.2 航班延误模式提取
由于间隔太短的子序列无法保证递归矩阵的有效性,而间隔太长的子序列又会导致一部分延误率模式变化被平滑忽略,因此,结合数据采样频率,经多次试验判断,间隔长度取阈值为18,即子序列的最大分割长度不能超过1.5 h.在Matlab7.9平台上实现了CUSUM算法,分割后共得到173条子序列.对这些子序列进行RQA,利用航班延误模式提取的方法,计算每个子序列的递归参数.同时,考虑到不同时段航班延误率的大小及子序列的波动水平,将描述子序列统计参数的均值和标准差引入进来,总共7个特征参数作为聚类的输入矢量.航班延误没有既定的模式分类,而模式提取的目的是为航班延误预测和延误状态评估提供先验知识,聚类个数太多会导致预测难度增加,太少会掩盖一些模式.因此,为了合理、科学地提取航班延误模式,根据文献[17]将延误划分为1、2、3、4个等级,结合该枢纽机场实际生产运行规定的蓝、黄、橙、红4个延误等级标准和民航局关于印发《民航航班正常统计办法》的通知取k=4.表1描述的是4种航班延误模式的聚类中心参数值以及每种模式在复显性以及统计特性等方面的特征.

表1 航班延误模式参数及统计特征
图4描述的是类中心参数归一化后的4种模式分布.模式4对应畅通状态,此时延误率均值最小,该模式中子序列的波动也最小,状态比较平稳,对应着航班起降较少的凌晨时段,5个递归参数均是4种模式中最大的,统计特征主要表现为具有复杂的确定性结构、复显性明显、具有一定的周期性,是一个较平稳的过程并且该模式下的系统状态变化较慢.畅通流在每天出现的时段基本相同,这与后面的时变分析是一致的.模式2对应轻度延误状态,主要出现在早高峰开始之前的时段,此时延误率较大,波动最大,递归参数是4种模式中最小的,统计特征主要表现为非线性、非平稳性,复显性最低(当前状态后续出现的可能性不大),结构不确定,该模式下的系统变化非常不稳定.模式1对应中度延误状态,主要在早高峰8:00-10:00和13:00-14:00左右时段出现,此时工作人员精力充沛,资源相对富足,延误尚在可控范围内.模式3对应高度延误状态,主要在9:00-11:00和15:00-19:00左右时段出现,延误时间普遍较长.模式1和模式3的各个参数非常接近,都具有较高的延误率,二者在早高峰之后交替出现,复显性较低.

图4 类中心参数归一化后的4种模式分布
3.3 时变特征分析
图5描述的是根据本文方法提取的一周延误率模式在每一天的分布情况,通过对比可以得到共同的延误模式特征.凌晨0点到早晨7点左右处于模式4畅通状态,结合表1中模式4的统计特征可知凌晨0点到7点左右的延误率具有较强的复显性以及确定性结构,周期性明显,模式4偶尔也会出现在23点左右,为航班延误预测提供了一定的先验知识,比如当某些数据丢失时就可以利用该段时间的数据通过简单的计算方法填补空缺值.模式2具有很强的随机性,出现时间很短,也就是系统变化很快,因此,在做预测时必须考虑加入非线性的约束.模式1和模式3在7点到24点之间交替出现,延误率较高,但是波动增加不多,递归参数相较于模式4均略有下降,说明模式1和模式3结构的复显性低于模式4,但是也有一定的周期性.航班延误时变分析与实际情况相符,这就为实施相关航班延误措施提供了理论依据,例如可以尽量减少模式2的出现,模式1和模式3尽可能多的转变为模式4:模式2延误率不大,但是随机性太强,波动大,出现时间没有规律,因此,可以在模式2即将出现之时,对相关延误航班进行重点监控、优先保障等,从而减少模式2对整个航空运输系统带来的扰动;模式1和模式3延误情况比较严重,二者交替出现在白天航班密集的时间段内,为了更好地对该段时间内的航班延误进行预警控制,可以在制定航班计划时避开高峰时刻,将航班错峰分流至航班平峰或者低谷时间段.尽管不一定能够降低整体延误率,但是单一的延误模式可以使整个系统处于可控制的状态,从而使未知的航班延误带有一定的可预见性.

图5 4种典型的延误模式在一周内每天的分布情况
4 结 论
1)首次将递归分析理论引入到航空运输领域,通过实例分析验证航班延误率时间序列的混沌特性,得到畅通、轻度延误、中度延误、高度延误4种典型的航班延误模式,并获得每种延误模式在一周内每一天的分布情况.
2)研究结果不仅有利于航空从业人员用超前的眼光和科学的方法来应对即将发生的延误,并提前采取相应措施,还在一定程度上减轻了后续延误航班恢复的工作量和恢复难度.这对于改善航班延误状况具有十分重要的理论意义和实际应用价值,为机场当局和航空公司开展航班延误工作的研究提供了一个全新的角度.
[1]ABDELGHANY K F,ABDELGHANY A F,EKOLLU G. An integrated decision support tool for airlines schedule recovery during irregular operations[J].European Journal of Operational Research,2008,185(2):825-848.
[2]JAFARI N,ZEGORDI S H.Simultaneous recovery model for aircraft and passengers[J].Journal of the Franklin Institute,2011,348(7):1638-1655.
[3]WONG J T,TSAIA S C.A survival model for flight delay propagation[J].Journal of Air Transport Management,2012,23:5-11.
[4]邵荃,罗雄,吴抗抗,等.基于贝叶斯网络的机场航班延误因素分析[J].科学技术与工程,2012,20(30):8120-8124.
[5]DELGADO L,PRATS X.Operating cost based cruise speed reduction for ground delay programs:effect ofscope length[J]. Transportation Research Part C:Emerging Technologies,2014,48:437-452.
[6]袁瑗,陈兵,徐涛,等.基于先验知识的多类CVM航班延误预警模型[J].吉林大学学报(工学版),2010(3):161-166.
[7]刘雄.基于枢纽机场的航班延误预警评价研究[D].广汉:中国民用航空飞行学院,2012.
[8]TAKENS F.Detecting strange attractors in turbulence[M]. Berlin,Heidelberg:Springer⁃Verlag,1981.
[9]王海燕.非线性时间序列分析及其应用[M].北京:科学出版社,2006.
[10]KIM H S,EYKHOLT R,SALAS J D.Nonlinear dynamics,delay times,and embedding windows[J].Physica D:Nonlinear Phenomena,1999,127(1):48-60.
[11]FRASER A M,SWINNEY H L.Using mutual information to find independent coordinates for strange attractors[J]. Phys.Rev.A,1986,33:1134-1140.
[12]宋晓,李平,徐公林,等.基于递归定量特征的变压器励磁涌流识别[J].中南大学学报:自然科学版,2013(5):1932-1937.
[13]XIAO Z,CHEN Z,DENG X.Anomaly detection based on a multi⁃class CUSUM algorithm for WSN[J].Journal of Computers,2010,5(2):306-313.
[14]MARWAN C,ROMANO M C,THIEL M,et al. Recurrence plots for the analysis of complex systems[J]. Physics Reports,2007,438(5):237-329.
[15]BASTOS J A,CAIADO J.Recurrence quantification analysis of global stock markets[J].Physica A:Statistical Mechanics and its Applications,2011,390(7):1315-1325.
[16]李新杰.河川径流时间序列的非线性特征识别与分析[D].武汉:武汉大学,2013.
[17]刘小飞.基于数据挖掘的航班延误预测模型及方法的研究[D].南京:南京航空航天大学,2010.
(编辑 张 红)
Two⁃stage extraction method for flight delay pattern
MENG Huifang,PENG Yi
(Optimization Laboratory of Civil Aviation Transportation,Nanjing University of Aeronautics and Astronautics,211100 Nanjing,China)
For the problem of severer flight delays,based on the relative research achievements in domestic and aboard,this paper proposes a two⁃stage method for extracting flight delay patterns.Firstly,this method uses the phase⁃space reconstruction theory and Recurrence Plot to analyze the chaotic characteristics of flight delay rate. Then,after acquiring the delay time subsequences,the Recursive Quantitative Analysis and K⁃means Clustering technology were used to extract flight delay patterns,and the characteristics of time⁃varying of flight delay patterns were analyzed.Finally,the example verifies this method can not only effectively extract flight delay patterns,but also can get the time⁃varying characteristics of the patterns.The resultprovides managerialand decisive reference of prediction and warning of flight delay for airports and airlines.
flight delay;phase⁃space reconstruction;chaotic characteristics;recurrence quantification analysis;delay pattern;time⁃varying characteristics
F56
A
0367-6234(2015)10-0070-06
10.11918/j.issn.0367⁃6234.2015.10.014
2014-11-04.
国家装备预研基金(NAA13002).
孟会芳(1988—),女,硕士研究生.
孟会芳,huifang_meng@sina.cn.

