不同初始组织材料超塑性m值模型与验证

曹富荣，崔建忠，丁 桦，侯红亮，李志强（.东北大学材料与冶金学院，089沈阳；.材料电磁过程教育部重点实验室（东北大学），089沈阳；.中航工业北京航空制造工程研究所，0004北京）

不同初始组织材料超塑性m值模型与验证

曹富荣1，崔建忠2，丁 桦1，侯红亮3，李志强3
（1.东北大学材料与冶金学院，110819沈阳；2.材料电磁过程教育部重点实验室（东北大学），110819沈阳；3.中航工业北京航空制造工程研究所，100024北京）

为确定超塑性机理和本构方程，需要计算m值.采用铸造、轧制和退火方法获得细晶AA7075铝合金板材，采用高温拉伸机和图像分析仪研究了合金m值的变化，针对等轴晶粒和带状晶粒的材料超塑性变形，建立了m值与应变关系模型.模型证明等轴晶粒组织恒速度超塑性变形m值随应变增加而减小和带状晶粒组织超塑性变形m值随应变增加而增大.理论预测得到等轴细晶AA7075铝合金和AA7475+0.7Zr铝合金和带状晶粒的Mg⁃8.5%Li合金和包含小角度晶界的AA7475铝合金超塑性实验结果的支持.模型预测与实验结果吻合，内在组织变化是m值变化的根本原因.

超塑性；应变速率敏感性；应变；空洞；动态再结晶

超塑性指多晶材料以各向同性方式表现出很高的拉断延伸率的能力［1］.文献［2］认为测量的经典超塑性延伸率＞400%，测量的应变速率敏感性接近0.5；文献［3］提出超塑性应变速率敏感性指数（m值）的概念，m值是衡量材料高温速控变形能力的极其重要的指标，不仅在超塑性中，而且在蠕变和热变形中得到了广泛的应用.该指数的理论模型国内外开展了深入研究，属于唯象学研究成果［4］.目前还没有报道把显微组织与m值和应变联系起来.

超塑性变形前的组织通常有两种：等轴晶粒组织和带状晶粒组织［5］.等轴晶粒组织超塑性变形期间发生晶粒长大和空洞发展.带状晶粒组织或称非理想组织通常发生应变诱发动态再结晶转化为等轴晶粒组织.例如，文献［6］对工业铝合金细晶超塑性研究提出两种方式：1）AA5083和AA7475合金静态再结晶获得变形前等轴细晶组织；2）AA2004和AA8090合金，其轧制与退火处理得到回复的带状组织，该带状组织在超塑性变形过程中亚晶演变为大角度晶界的等轴晶粒.研究表明两种组织的力学行为明显不同［7］.由于力学特征的变化，作为揭示机理的m值在两个过程中的变化必然不同.文献分析发现，m值与应变的关系目前没有从理论上证明和验证.因此本文获得了材料超塑性m值与应变关系模型，列举实验证据证明模型的合理性.

1 理论推导与分析

1.1 等轴晶超塑性m值与应变ε关系模型

超塑性变形通常采用两种过程：恒速度变形和恒应变速率变形.对恒速度拉伸变形，如果应变采用工程应变εe，得到［8］

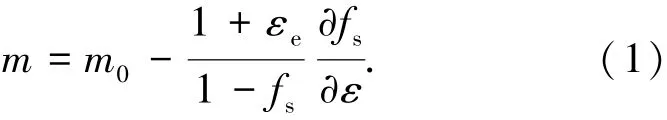
式中：σ0为无空洞时材料流动应力；fs为空洞面积分数；m0为无空洞时材料的m值.

如果应变采用真应变εt，得到

式中：η为空洞长大因子，对单向拉伸为确定值；V0为零应变时的空洞体积分数.

将式（4）代入式（1）～（3），恒速度超塑性过程m值与应变ε关系式为：

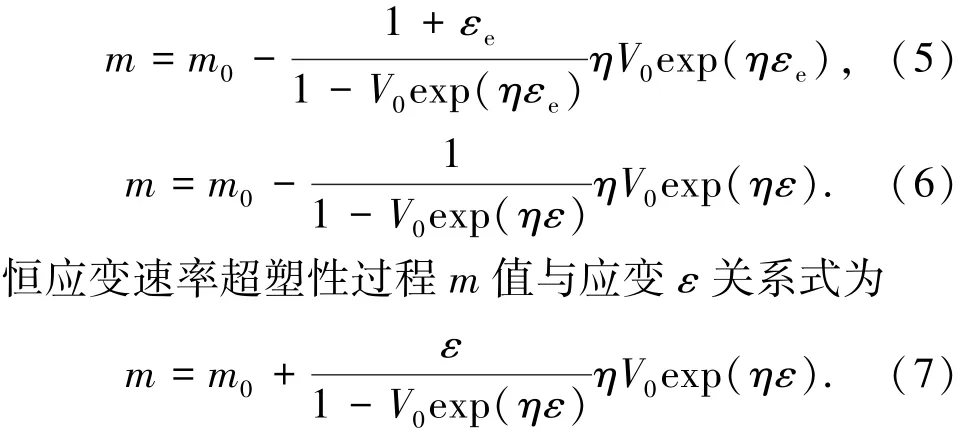
因此，由式（5）和式（6）断定恒速度超塑性过程m值随应变增加而减小.所以，等轴晶粒组织恒速度超塑性变形应变速率敏感性指数随应变增加而减小得到证明.

另一方面，由式（7）断定恒应变速率超塑性过程m值随应变增加而增大.变形过程中m值增大意味着晶界滑移的贡献增加，有利于超塑性能力的发挥.

1.2 带状组织动态再结晶诱发超塑性过程m值与

应变ε关系模型

高温变形本构方程一般可表示为［10］

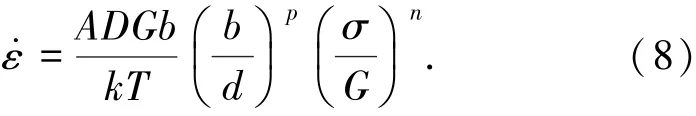
式中：A为量纲一的常数；D为扩散系数；G为剪切模量；b为位错柏氏矢量的模；k为玻尔兹曼常数；T为温度；d为晶粒尺寸；σ为外加应力；p为晶粒指数；n为应力指数，n＝1／m.

对一般动态再结晶热变形过程，令p＝0，并采用动态再结晶模型σ＝C／d，其中C为常数.设温度T一定，则B与G一定，C为常数，应变速率ε·恒定（对恒速率变形过程）或应变速率ε·随应变增加而减小（恒速度变形过程），由于动态再结晶过程d＝F／ε，这里F为常数，将σ与d关系代入式（8）得

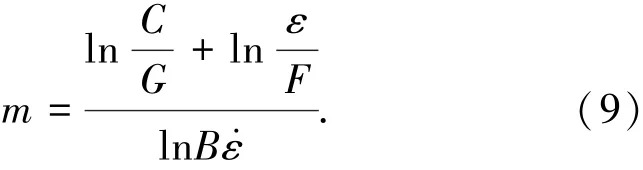
式中：B＝1／［（A′D）／b2］和A′＝［ADGb3］／（kT）.由式（9）可见随应变ε增加，m值增大.

对带状晶粒超塑性变形，由于应变诱发动态再结晶，发生小角度晶界向大角度晶界的转变，在达到动态再结晶临界应变εc（通常εc＜50%，个别80%）后随应变增加逐步转变为等轴晶粒，此时p＝2或p＝3，仍然采用σ＝C／d关系模型.设温度T一定，则A与D一定，C和b为常数，应变速率ε·同上，由于动态再结晶过程d＝F／ε，这里F为常数，将σ与d关系代入式（8）得

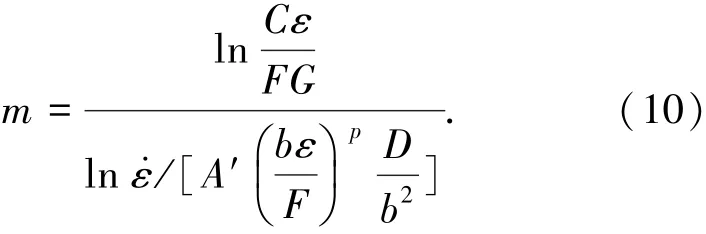
由式（10）可见随应变ε增加，m值增大.式（9）和式（10）均证明带状晶粒组织高温热变形和超塑性变形的m值随应变增加而增大.

2 实验验证与分析

2.1 等轴晶超塑性m值与应变ε关系模型实验验证

本文采用熔铸、轧制和退火方法获得AA7075（Al⁃Zn⁃Mg）合金等轴晶板材，合金成分为：Zn 4%～5%，Mg 2%～3%，Zr、Mn、Cr合计0.5%，其余为铝.板材晶粒尺寸为9.4μm，为细晶组织.超塑性变形采用恒速度拉伸.空洞面积分数采用计算机图像分析获得.因而获得空洞体积分数V.m值采用Backofen方法测量.图1为4种变形条件下的空洞体积分数与应变的关系.把图1实验数据代入式（1）或式（5），得到m值与应变ε关系曲线，如图2所示.可以看出实验测量值与模型计算值吻合.说明AA7075合金等轴晶超塑性恒速度拉伸过程m值随应变增加而减小.

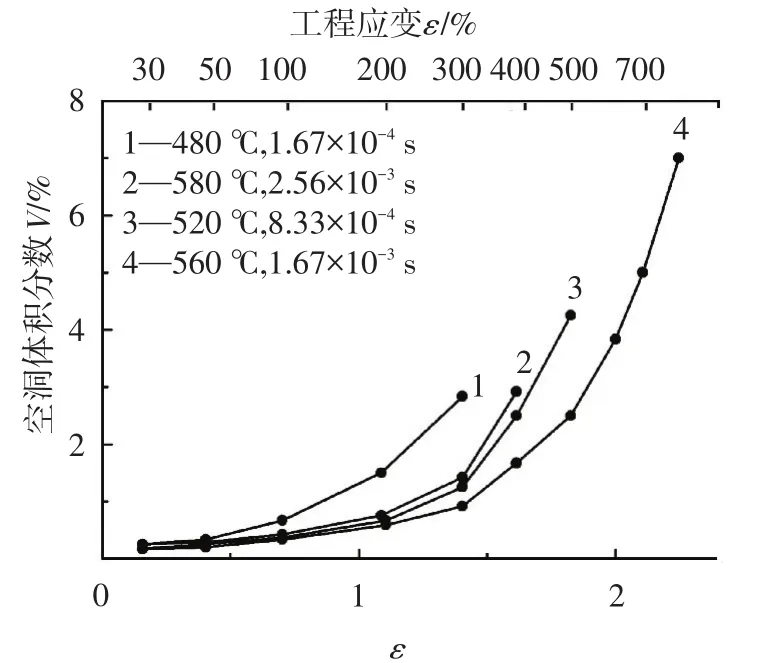
图1 AA7075合金空洞体积分数与应变曲线

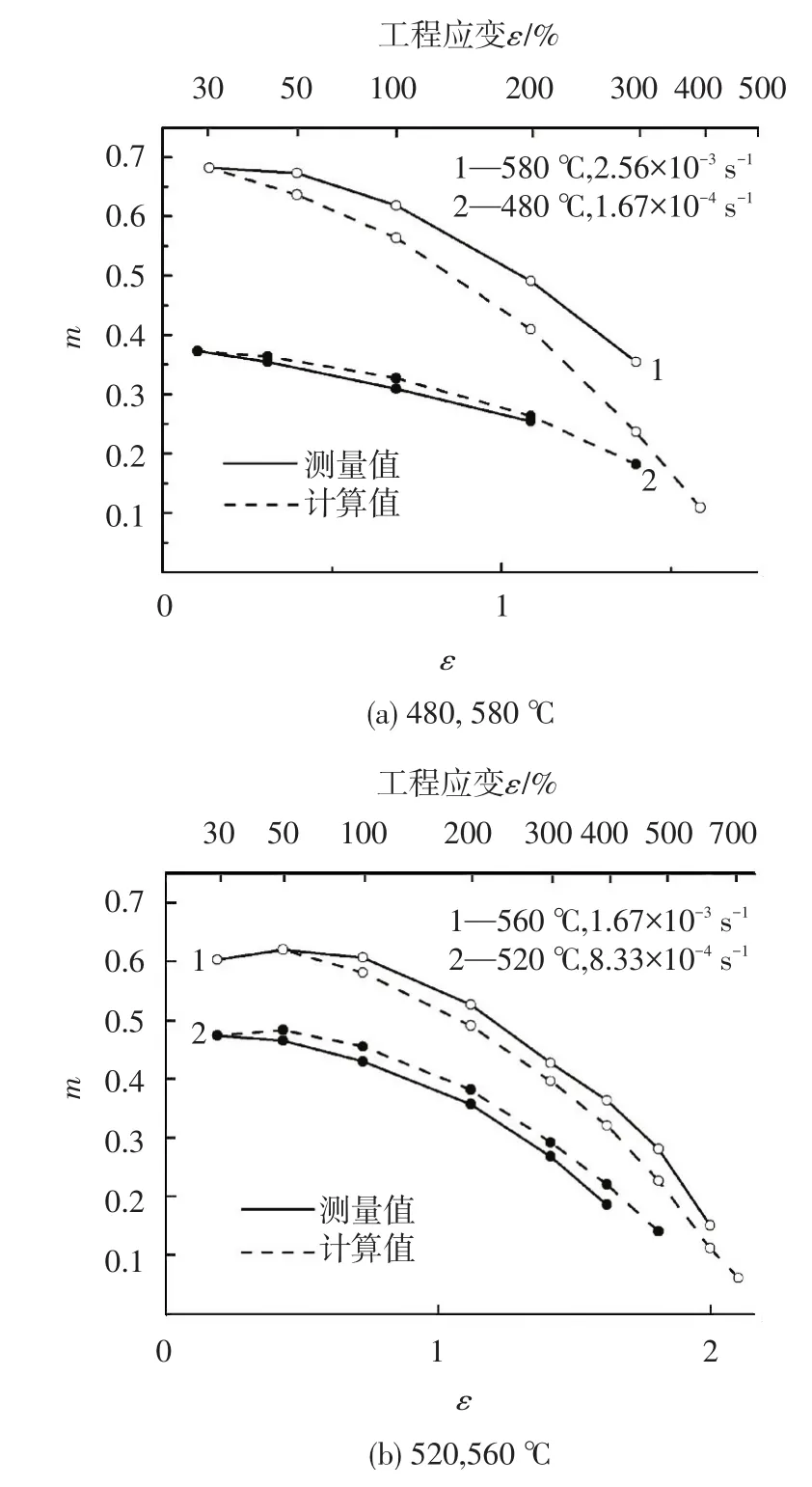
图2 AA7075合金m值与应变ε关系曲线

文献［11］采用粉末冶金和挤压方法制备了AA7475+0.7Zr铝合金，等轴晶尺寸为2μm.超塑性变形采用恒速度拉伸.m值采用Backofen方法测量.获得的m（此处为ma表观m值）与应变ε关系曲线，如图3所示.可见该合金等轴晶超塑性恒速度拉伸过程m值随应变增加而减小.

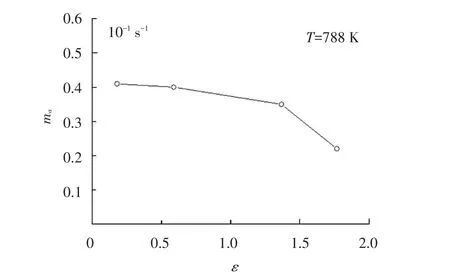
图3 AA7475+0.7Zr铝合金等轴晶788 K，10－1s－1条件下m值与应变ε关系

2.2 带状组织动态再结晶诱发超塑性m值与应变ε关系模型实验验证

文献［12］采用熔铸、473 K轧制获得了带状晶粒的Mg⁃8.5%Li合金板材.带状晶粒组织超塑性变形采用恒应变速率拉伸，m值采用Backofen方法测量.实验发现随应变增加，带状晶粒向等轴晶粒的转变，获得了m值与应变ε关系实验曲线，理论计算结果与实验结果对比如图4所示.应变在0.1～0.9之间，m值在0.41左右波动；应变在0.9～1.5之间，随应变ε增加m值由0.41逐渐增加到0.68；应变超过1.5之后，由于晶粒长大和空洞长大，m值逐渐降低.可见应变0.9～1.5之间的m值，测量值与计算值十分吻合.

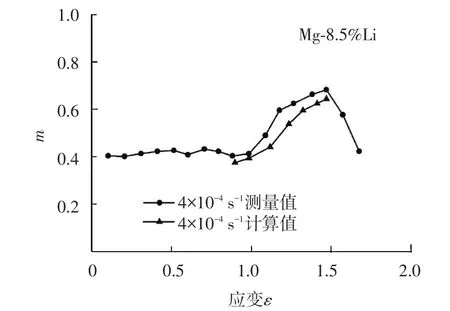
图4 Mg⁃8.5%Li合金m值与应变ε关系曲线

在包含小角度晶界的非理想组织中，文献［13］研究AA7475铝合金超塑性m值时发现，在温度788 K，应变速率10－1s－1条件下真应变从0增加到1.7，测量的m值从0.30增大到0.55.根据变形前后晶界取向角的测量，认为随应变增加，晶界取向角逐渐增加是造成m随应变增加而增加的重要原因.文献［11］采用粉末冶金和挤压方法制备了AA7475+0.7Zr铝合金，获得真实应变速率敏感性mt与应变的关系，如图5所示.可见在应变ε≤0.4和1.4之前，mt随应变ε增加而增加.小角度晶界转化为大角度晶界是造成mt增加的组织原因.在应变ε≥0.4和1.4之后由于晶粒长大，发生mt的减小.

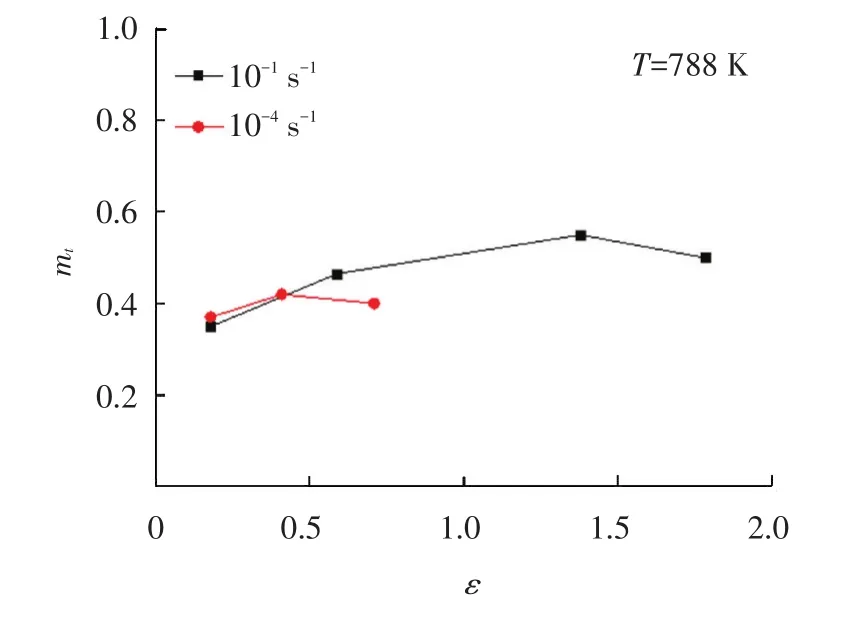
图5 AA7475+0.7Zr铝合金小角度晶界组织m值与应变ε关系

从实验证据与模型预测结果可以看出本模型的实验对象为等轴细晶（1μm＜d≤10μm）和带状组织，带状组织不是细晶，只有经过一定应变变形之后才转化为等轴细晶.模型预测得到了超塑性实验证据的支持.

3 讨 论

3.1 晶粒尺寸对m值的影响

对等轴晶材料（AA7075铝合金和AA7475+ 0.7Zr铝合金），AA7075铝合金在温度480～580℃，应变速率1.67×10－4～1.67×10－3s－1条件下，AA7475+0.7Zr铝合金在温度788 K，应变速率10－1s－1条件下，随变形进行，变形后晶粒尺寸大于变形前晶粒尺寸.大量证据表明许多材料发生变形诱发晶粒长大，由于晶粒长大，空洞在不利位向处形核与长大变得容易，使晶界滑移的贡献降低，因此m值降低.对带状组织材料（Mg⁃8.5%Li镁合金和AA7475+ 0.7Zr铝合金），Mg⁃8.5%Li镁合金在623 K，4×10－4s－1条件下，AA7475+0.7Zr铝合金在温度788 K，应变速率10－4～10－1s－1条件下，随变形进行，由于动态再结晶诱发晶粒细化，变形后晶粒尺寸小于变形前晶粒尺寸，空洞容易在不利位向处发生弥合，导致形核与长大变得困难，晶界滑移的贡献增加，因此m值增加.

3.2 通过空洞含量来确定m值与应变关系的适用性

一些材料在超塑性变形初期空洞形核阶段，由于空洞形核尺寸通常在1μm以下，光学显微镜无法分辨，随着空洞随变形的进行逐渐长大，在变形后期发展为尺寸较大的空洞，此时显微镜容易分辨.早期研究认为超塑性不存在空洞，但是后来陆续发现一些材料超塑性存在空洞.等轴晶超塑性m值与应变ε关系模型适用于有空洞的材料.

超塑性是材料在一定晶粒尺寸下和一定温度与应变速率条件下的变形行为.对恒速度拉伸过程，由于细晶超塑性通常是恒温超塑性，温度一定，剩下的变量就是应变速率，容易证明恒夹头拉伸速度下应变速率与工程应变成反比.恒速度拉伸过程应变速率降低，工程应变增加.因此m值降低.可以看出，m值对应变速率的变化与m值对工程应变的变化是一致的.

3.3 m值变化的内在组织演变原因

图2（b）、图4和图5中的m值与应变的关系都不是简单的单调规律，说明了超塑性的复杂性，内在组织变化才是m值上升、下降甚至水平波动的根本原因.图4的双相Mg⁃8.5%Li镁合金623 K，4×10－4s－1条件下组织研究发现，在应变0.9之前，组织为带状晶粒，此时m值随应变水平波动.在应变0.9之后到应变1.5之间，发生动态再结晶晶粒细化，m值上升，应变超过1.5之后，组织中晶粒长大同时发生明显的空洞长大，m值下降.AA7075铝合金图2（b）中的曲线1在560℃，应变速率1.67× 10－3s－1条件下，工程应变在30～50%之间m值上升与存在的少量带状晶粒转化为等轴晶有关，应变超过50%之后一直到断裂，晶粒与空洞长大，m值一直下降.AA7475铝合金图5在温度788 K，应变速率10－4～10－1s－1条件下，起初m值上升与小角度晶界转变为大角度晶界组织有关，在应变ε≥0.4和1.4之后由于晶粒长大与空洞长大，发生m值下降.由于内在组织的变化，引起力学行为的变化，从而引起特征参数m值的变化.文献［4］提出m值不是常数，是变数的观点以及把力学行为与微观物理衔接研究的观点在本文得到体现与证明.

4 结 论

1）针对等轴晶粒的材料超塑性变形，建立了超塑性m值与应变关系模型.证明了恒速度超塑性过程m值随应变增加而减小.理论预测与等轴细晶AA7075（Al⁃Zn⁃Mg）铝合金和AA7475+0.7Zr铝合金实验结果吻合.

2）针对带状晶粒或非理想组织的材料超塑性变形，建立了超塑性m值与应变关系模型.证明了m值随应变增加而增大.理论预测与带状晶粒的双相Mg⁃8.5%Li镁合金和包含小角度晶界的AA7475铝合金超塑性实验结果吻合.

3）分析发现：在温度一定，应变速率一定的条件下，m值随应变的上升与下降与内在组织变化有关；m值上升与小角度晶界的带状晶粒动态再结晶转变成大角度晶界的等轴晶粒有关；m值下降与等轴晶的晶粒长大和空洞长大有关.

［1］ZHAO Shasha，QAYYUME R，DIAO Haoyan，et al.Me⁃chanical and microstructural characteristics of superplastic Al⁃4.42Mg aluminum alloy［J］.Journal of Harbin Institute of Technology（New Series），2013，20（5）：96－100.

［2］LANGDON T G.Seventy⁃five years of superplasticity：historic developments and new opportunities［J］.Journal of Materials Science，2009，44（22）：5998－6010.

［3］BACKOFEN W A，TURNER I R，AVERY D H. Superplasticity in an Al⁃Zn alloy［J］.Transactions of ASM，1964，57（4）：980－990.

［4］宋玉泉，管志平，李志刚，等.应变速率敏感性指数的理论和测量规范［J］.中国科学：E辑，2007，37（11）：1363－1382.

［5］曹富荣.金属超塑性［M］.北京：冶金工业出版社，2014.

［6］SOTOUDEH K，RIDLEY N，HUMPHREYS F J，et al. Superplasticity and microstructural evolution in aluminum alloys［J］.Materialwissenschaft und Werkstofftechnik，2012，43（9）：794－798.

［7］MISHRA R S，BIELER T R，MUKHERJEE A K. Superplasticity in powder metallurgy aluminum alloys and composites［J］.Acta Metallurgica et Materialia，1995，43（3）：877－891.

［8］崔建忠.超塑性［M］.河北：河北教育出版社，1996.

［9］STOWELL M J，LIVESEY D W，RIDLEY N.Cavity coalescence in superplastic deformation［J］.Acta Metallurgica，1984，32（1）：35－42.

［10］LANGDON T G.Unified approach to grain boundary sliding in creep and superplasticity［J］.Acta Metallurgica et Materialia，1994，42（7）：2437－2443.

［11］KIM W J.Variation of true strain⁃rate sensitivity exponent as a function of plastic strain in the PM processed superplastic 7475Al+0.7Zr alloy［J］.Materials Science and Engineering A，2000，277（1／2）：134－142.

［12］HIGASHI K，WOLFENSTINE J.Microstructural evolution during superplastic flow of a binary Mg⁃8.5wt.%Li alloy［J］.Materials Letter，1991，10（7／8）：329－332.

［13］HIRATA T，MUKAI T，SAITO N，et al.Microstructural dynamics during high⁃strain⁃rate superplastic flow in PM 7475 alloy［J］.Materials Science Forum，1999，304－306：333－340.

（编辑 张 红）

Modeling the m value and its experimental verification during superplasticity of materials with different initial microstructures

CAO Furong1，CUI Jianzhong2，DING Hua1，HOU Hongliang3，LI Zhiqiang3
（1.School of Materials and Metallurgy，Northeastern University，110819 Shenyang，China；2.Key Laboratory of Electromagnetic Processing of Materials，Ministry of Education（Northeastern University），110819 Shenyang，China；3.Professor of AVIC Beijing Aeronautical Manufacturing Technology Research Institute，100024 Beijing，China）

In order to ascertain superplastic mechanism and establish constitutive equation，strain rate sensitivity exponent（m value）is required to be calculated.Fine⁃grained AA7075 aluminum alloy sheets were fabricated by casting，rolling and annealing，and variation in the m values were investigated by high temperature tensile machine and image analyzer.Aiming at the superplastic deformation of materials with the equiaxed grain and the elongated grain microstructures，the relations between the m value and the strain were modeled.It is noted that the m value for the equiaxed grain microstructure decreases with increasing the strain during constant velocity tension，and the m value for the elongated grain microstructure increases with increasing the strain during superplasticity.Theoretical predictions were verified by the superplastic experimental evidence in AA7075 alloy and AA7475+0.7Zr alloy with fine equiaxed grains and in Mg⁃8.5%Li alloys with the elongated grains and AA7475 alloy with low angle grain boundaries.The calculated results agree well with the experimental ones，and it is shown that variation in microstructure leads to the variation in the m value.

superplasticity；strain rate sensitivity exponent；strain；cavitation；dynamic recrystallization

TG136

A

0367－6234（2015）10－0050－05

10.11918／j.issn.0367⁃6234.2015.10.010

2014－06－11.

国家自然科学基金（51334006）.

曹富荣（1964—），男，博士，副教授；崔建忠（1950—），男，教授，博士生导师.

曹富荣，cfr⁃lff＠163.com.