导弹编队协同攻击分布式鲁棒自适应控制

周慧波，宋申民，郑 重

（1. 哈尔滨师范大学 数学科学学院，哈尔滨 150009；2. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001）

导弹编队协同攻击分布式鲁棒自适应控制

周慧波1,2，宋申民2，郑 重2

（1. 哈尔滨师范大学 数学科学学院，哈尔滨 150009；2. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001）

在有向通信拓扑下研究了导弹编队的鲁棒自适应协同跟踪控制问题。针对导弹编队系统中队形跟踪、外部扰动和模型不确定性的情况，通过选取包含位置跟踪误差和速度跟踪误差的辅助变量，提出了一种基于有向通信拓扑的鲁棒自适应编队控制策略。提出了自适应律对未知参数进行估计，并且利用Lyapunov稳定性理论分析了闭环系统的渐近稳定性。进一步，对于通信时滞的情况，给出了系统渐近稳定所需要满足的条件。与滑模控制等传统鲁棒控制不同，所设计的鲁棒自适应控制器是连续的，更便于导弹编队系统的实现。数值仿真结果表明，队形跟踪误差小于0.03 m，队形保持误差小于0.07 m，所设计的控制器能实现高精度的编队跟踪控制。

导弹编队；协同攻击；通信时滞；鲁棒自适应控制；有向图

由于反导防御系统的迅速发展，单枚导弹攻击目标已经越来越难以独立完成作战任务，难以适应现代化战争的需要。多枚导弹组成编队飞行系统，同时在作战过程中导弹通过信息交互进行协同攻击，共同完成作战任务，极大地增强了打击能力和摧毁目标的概率，显著提高导弹的突防能力，因此对多弹协同攻击的研究具有非常重要的现实意义。

在导弹协同攻击过程中，为了合理有效地利用陆、海、空的地形信息形成有掩护的攻击或规避，需要考虑所处的战场环境，实时根据不同的地形和目标信息设计编队队形控制律[1]。简单地说，队形控制就是指利用多个导弹在编队飞行过程中组成一定的编队构形，并实时地保持或收缩。编队成员通过通信相互联系，进行协同工作，控制编队成员间的相对距离和方向，并保持所要求的几何构形。为了实现高精度的编队飞行任务，需要对各编队成员进行有效的协同控制。编队协同控制方法一般包括多输入多输出控制、虚拟结构控制和基于行为的控制[2]。目前这些方法在机器人编队[3-4]、航天器编队[5-6]和导弹编队[7]中得到了应用。对于多导弹协同攻击的方法主要有动态面控制法[8-9]、最优控制理论等[10-11]。

对于导弹编队协同问题，目前大多文献主要研究基于到达时间一致的协同制导[12-14]，其主要思想是利用一致性算法的思想，通过设计制导律使得各导弹能够同时到达目标，即实现了对目标的协同攻击。然而，当导弹编队执行协同作战任务时，需要进行队形的调整：初始队形的生成，队形的保持、收缩、扩展和重构等等。因此对导弹编队飞行控制系统的研究十分重要，直接决定上述导弹编队动作能否实现，以致影响到作战任务能否顺利完成[12]。文献[15]利用线性LQ最优控制理论设计了一种导弹编队队形最优保持控制器，能够实现导弹编队队形快速、稳定的调整与保持控制。文献[16]通过解黎卡提矩阵微分方程的形式设计了一种导弹协同攻击编队非线性最优控制器。

然而以上文献在设计导弹编队控制器时并没有考虑外界扰动的影响。在导弹飞行过程中，气流、强风等外界扰动往往是不可忽略的，在导弹编队控制器设计中必须考虑抑制扰动的要求。同时，为了形成编队队形，导弹之间往往会通过通信进行协同控制，在此过程中可能发生通信时滞。因此在设计控制器时必须要考虑通信时滞的影响。

针对导弹编队飞行系统，本文提出了鲁棒自适应导弹编队协同控制策略，并严格分析了闭环系统的Lyapunov 稳定性。首先，在无通信时滞的情况下提出了自适应律对扰动的上界进行估计，并进一步设计了导弹队形控制算法。在此基础上，考虑到外部扰动和通信时滞的情况，通过Lyapunov 稳定性分析给出了系统渐近稳定所需要的条件。最后数值仿真验证了所提出的鲁棒自适应控制器的有效性。

1 导弹编队飞行系统

假设n枚导弹在三维空间中组成编队飞行系统，则第i枚导弹的运动可由下面方程描述[1]：

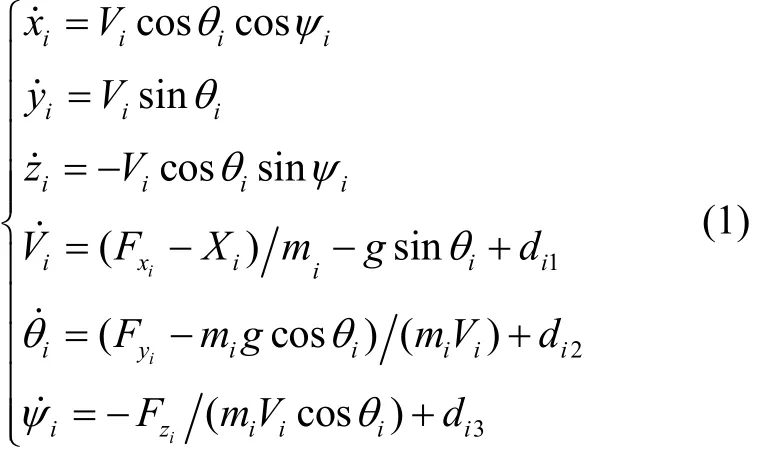
式中：(xi,yi,zi)表示导弹的位置；Vi、θi和ψi分别表示导弹速度、弹道倾角和弹道偏角；mi为导弹的质量；Xi为阻力，具体数值与阻力系数cx、空气密度ρ、速度Vi和导弹特征面积Si有关，计算公式为

Fi=[FxiFyiFzi]T表示导弹控制力向量；di=[di1di2di3]T表示导弹受到的扰动，并假设di有界且满足di∞≤。令pi=[xiyizi]T表示导弹的位置，vi=[iii]T表示导弹速度。则式(1)可表示为[1]

在导弹编队进行机动控制中，往往有队形保持要求。记第i枚编队导弹期望位置=+piF，其中：为编队中心的期望位置，为事先规划好的路径；piF为第i枚导弹相对于编队中心的期望位置。注意到，pi→pid和i→意味着实现了跟踪的要求，意味着实现了队形保持要求。因此本文目的为针对导弹编队运动模型(3)，设计控制器Fi，使得对于∀i,j=1,2,…,n，当t→∞时，有pi→和vi→；同时在跟踪误差pi-和vi-的暂态收敛过程中，在一定程度上保证pi-piF→pj-pjF和vi-viF→vj-vjF。

在导弹编队系统中，导弹通过信息交互获得其它导弹的状态信息以完成编队任务，这种信息交互可以通过图论来描述。加权图G=(ν, ζ, C)由节点集ν={1,2,…n}、边集ζ和加权邻接矩阵C=[cij]∈Rn×n组成。如果第j个节点有信息传递到第i个节点，则第j个节点有一条边指向第i个节点，记为(j,i)∈ζ。同时C中元素cij定义为：如果(j,i)∈ζ，则cij＞0，否则cij=0。有向图的路径指一列节点v0,…vr，(vi,vi+1)都是有向图中的边，i=0,…,r-1。如果有向图中任意两个节点均有路径相连，则称为强连通的。

引理 1[17]图G的Laplace矩阵L定义为

如果L是一个强连通的有向图的Laplace矩阵，则存在一个所有元素均为正的向量使得ηTL=0。

2 队形协同跟踪控制器

为了实现导弹编队的要求，导弹编队成员需要跟踪各自的期望位置和期望速度。本节首先给出无通信时滞的鲁棒协同控制器；在此基础上，考虑到通信时滞的情况，设计时滞鲁棒自适应协同控制器。

记跟踪误差ei=pi-，则˙i=vi-，定义辅助误差变量为

式中：λi＞0为常数。首先给出下面引理。

引理2[18]对于任意的实数x和非零实数y，下面不等式成立：

式中：α＞0，其最小值α*满足α*=x*(1-tanhx*)，x*满足方程e-2x*+1-2x*=0。

2.1 无通信时滞控制器设计

假设导弹质量已知且导弹之间的信息交互无通信时延，即导弹可以实时获取相邻导弹的信息。由式(3)和式(4)可得：设计自适应鲁棒控制器为

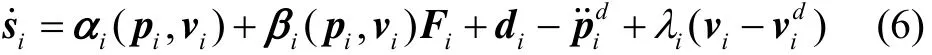
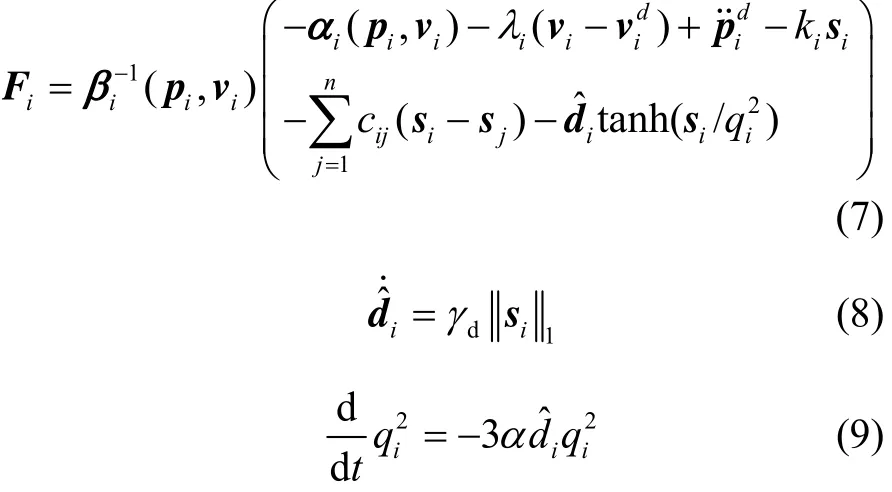
式中：常数ki＞0；cij表示加权邻接矩阵C的第i行j列元素；i为扰动上界i的估计值，且满足i(0)＞0；常数γd＞0；参数qi是时变的且满足qi(0)＞0；常数α如引理2所定义。把式(7)代入到式(6)，可得系统闭环方程为

定理1 对于导弹编队系统(3)，设计鲁棒控制器(7)-(9)，如果导弹之间的通信拓扑为强连通的有向图，则系统状态pi和vi全局一致有界，并且当t→∞时，有ei→0和˙i→0成立，从而有pi-piF→pj-pjF，成立。即实现导弹对期望轨迹的跟踪，同时形成并保持所期望的队形。

证明 引理2中的不等式(5)可以写为

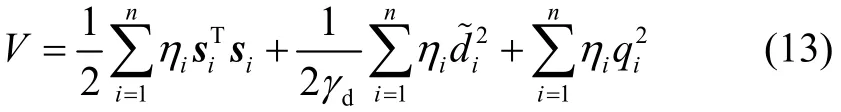
式中，常数ηi＞0如引理1所定义。对式(13)求导，并且利用式(8)～(10)，可得：

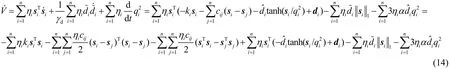
把式(12)代入式(14)可得

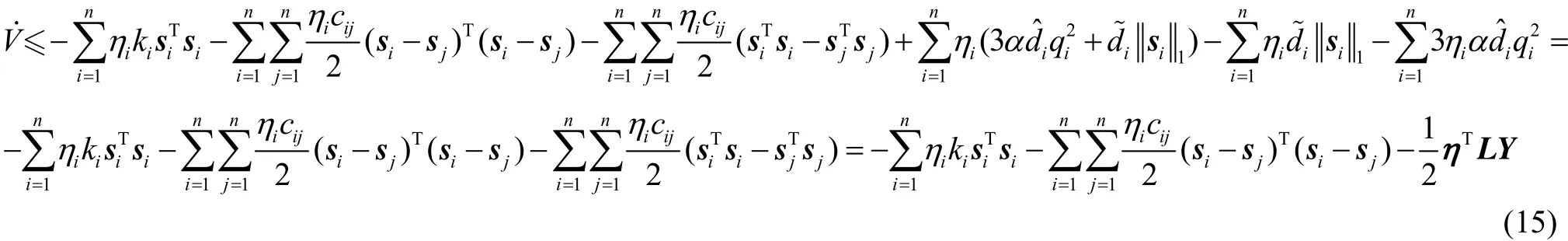
由式(16)可以看出V有界，因此系统状态pi和vi全局一致有界。

由于V有界，则si,i∈L∞。由于扰动di有界，由式(10)可得˙i∈L∞。此外，由V是有界的并且≤0可得，这表明si∈L2。因此由Barbalat>引理[19]可得，当t→∞时，si→0，因而由si的定义可得ei→0和e˙i→0。由于因此pi-piF→pj-pjF成立。同理可得vi-→vj-。因此鲁棒编队控制器(7)-(9)能够实现导弹对期望轨迹的跟踪，同时形成并保持所期望的队形。

2.2 通信时滞情况下的控制器设计

为了实现导弹的编队控制，要求导弹获得相邻导弹的状态信息，这些信息一般是通过无线传输进行信息交互。由于导弹之间的距离和传输设备物理限制的影响，信息传输中不可避免地存在通信时滞，并且时滞一般是不可忽略的。在2.1节基础上，本节进一步考虑编队系统中存在通信时滞的情况，即实际情况中第i枚导弹只能获取时滞后的信息sj(t-Tij)，即此时控制器(7)变为

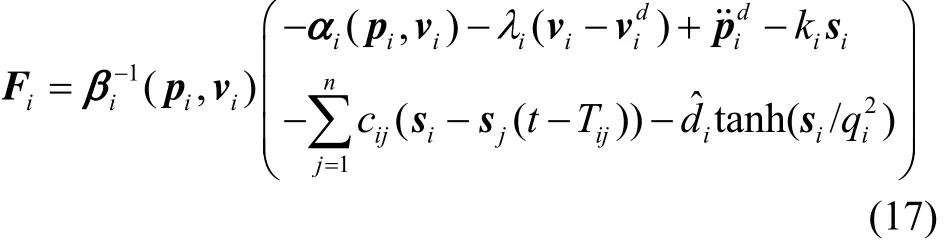
式中：Tij(t)≥0是时变的并且不要求Tij=Tji。假设Tij的精确值是未知的，而T˙ij的上界是已知的，且满足ij≤hij＜1。下面给出了考虑通信时滞的导弹编队控制器(17)的稳定性分析，表明在控制器参数满足一定条件下，对于时变的通信时滞，系统仍然能够实现导弹的编队跟踪控制。

定理 2 对于导弹编队系统(3)，设计鲁棒自适应控制器(17)和(8)(9)，如果导弹之间的通信拓扑为强连通的有向图，且对于任意的i,j=1,2,…,n，控制器参数满足

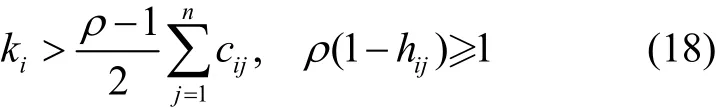
式中：常数ρ＞1，则系统状态pi和vi全局一致有界，并且当t→∞时，有ei→0和˙i→0成立，从而有pi-piF→pj-pjF，vi-v→vj-v成立。即存在通讯时滞情况下，导弹仍然能实现对期望轨迹的跟踪，同时形成并保持所期望的队形。

证明 选取Lyapunov函数

由式(17)和定理1的证明过程可得，V的导数为

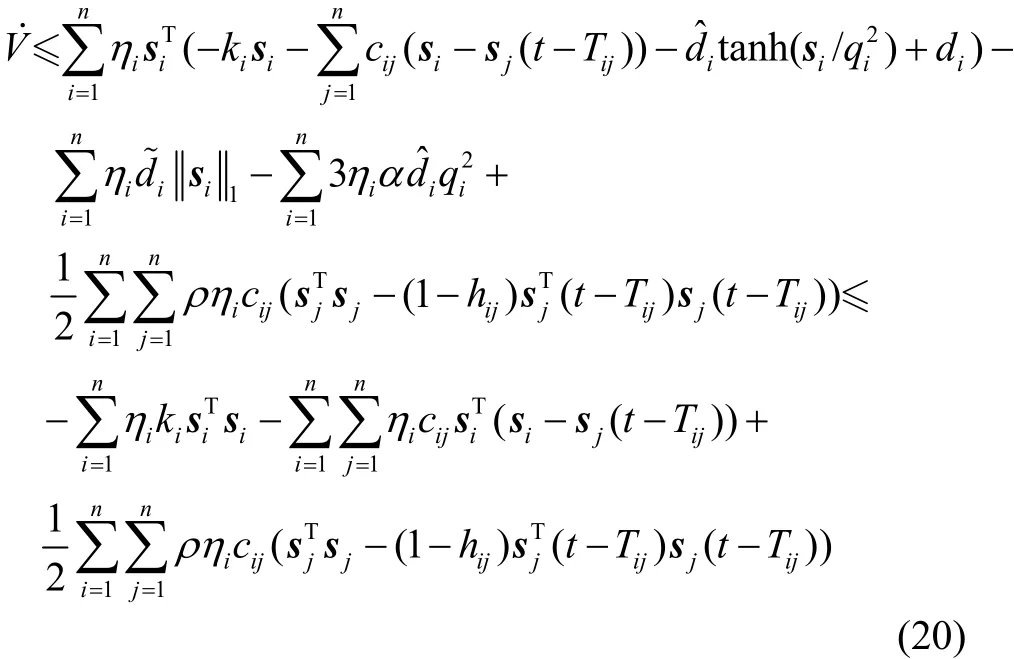
注意到

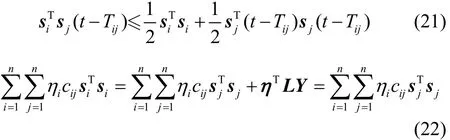
把式(21)和式(22)代入到式(20)中，可得

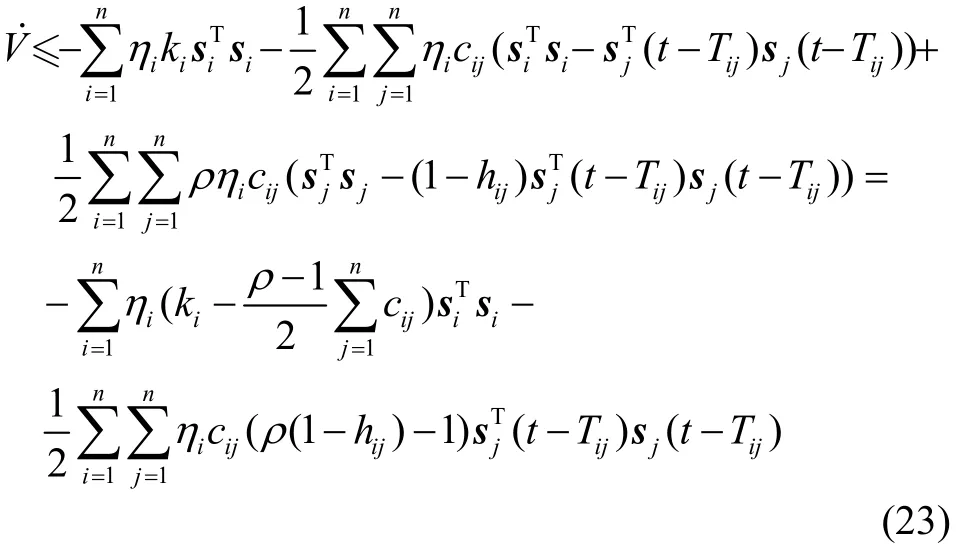
因此，如果条件(18)成立，则有

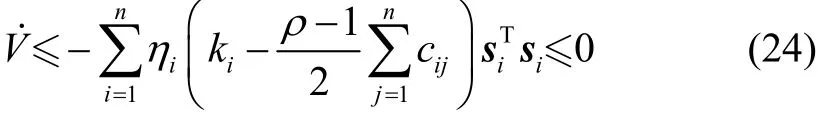
从而V有界，系统状态pi和vi全局一致有界。由于V有界，则si,i∈L∞。由于扰动di有界，由式(10)可得˙i∈L∞。此外，由V是有界的并且≤0可得这表明si∈L2。因此由Barbalat引理[16]可得，当t→∞时，si→0，因而由si的定义可得由于因此pi-piF→pj-pjF成立。同理可得

3 数值仿真分析

3.1 仿真参数设定

为了验证本文所设计控制器的有效性，下面针对存在通信时滞情况下的控制器(17)及(8)(9)进行仿真验证。

2016年8月，新的北辰基督教堂建成启用。新教堂建筑面积12000平方米，最高处24米，阶梯式大厅可容纳2500人。

4枚导弹进行正方形编队，设导弹质量分别为m1=150 kg, m2=200 kg, m3=180 kg, m4=160 kg。令wi=[Viθiψi]T，编队导弹初始状态和速度设为

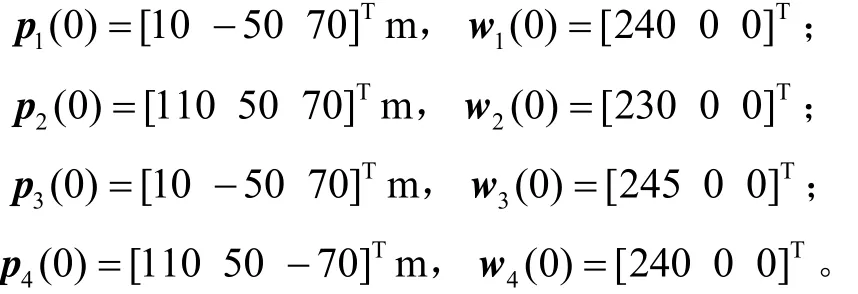
设定编队导弹相对于编队中心的期望位置为

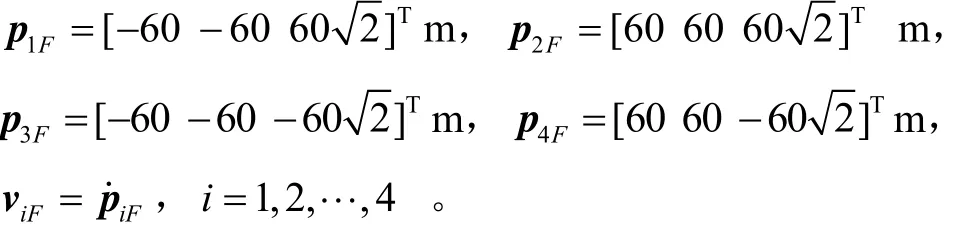
编队中心的期望位置和速度为

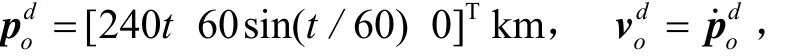
则编队导弹要跟踪的期望位置和速度为

控制器的参数选取为：λi=2，ki=0.2，

3.2 仿真结果与分析

图1 编队导弹相对运动轨迹Fig.1 Trajectory of relative motion of formation missiles

从4枚导弹编队初始位置和期望的正四边形编队构形可知，暂态过程中1μ越小，队形跟踪误差越小；2μ越小，队形保持性能越好。

控制器(17)及(8)(9)作用下的编队系统仿真结果如图1～图5所示。在仿真图中角标i表示第i枚导弹。图1给出了4枚编队导弹在惯性坐标系下的三维运动轨迹，可以看到编队导弹实现了正四边形的队形要求。图2和图3分别给出了编队导弹位置跟踪误差和速度跟踪误差曲线。从图2中可以看出，在设计的控制器(17)及(8)(9)作用下，即使存在外部扰动和通信时滞的限制，位置跟踪误差仍能够较快收敛到零附近。从图3可以看出，编队导弹速度跟踪误差最终也收敛到零附近，同时具有较高的跟踪精度。图4进一步给出了控制器(17)及(8)(9)作用下的队形跟踪误差μ1和队形保持误差μ2的变化曲线，从图中可以看出队形跟踪误差和队形保持误差收敛速度较快，同时最终队形跟踪误差小于0.03 m，队形保持误差小于0.07 m，具有较高的精度。图5给出了控制器中自适应参数i和的变化曲线。从图5中可以看出，自适应参数i最终收敛到常值，单调下降，由于下降速度远小于位置跟踪误差和速度跟踪误差的收敛速度，既保证了抑制外界干扰的鲁棒性又避免了控制器抖振。

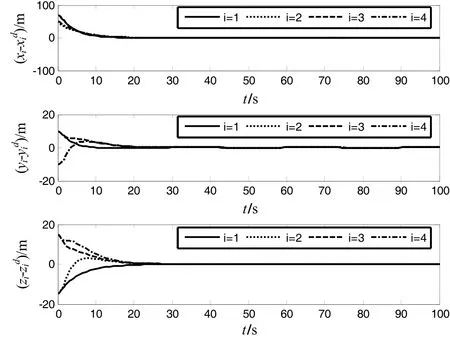
图2 位置跟踪误差Fig.2 Position tracking errors

图3 速度跟踪误差Fig.3 Velocity tracking errors

图4 队形跟踪误差和队形保持误差Fig.4 Errors of formation tracking and formation keeping

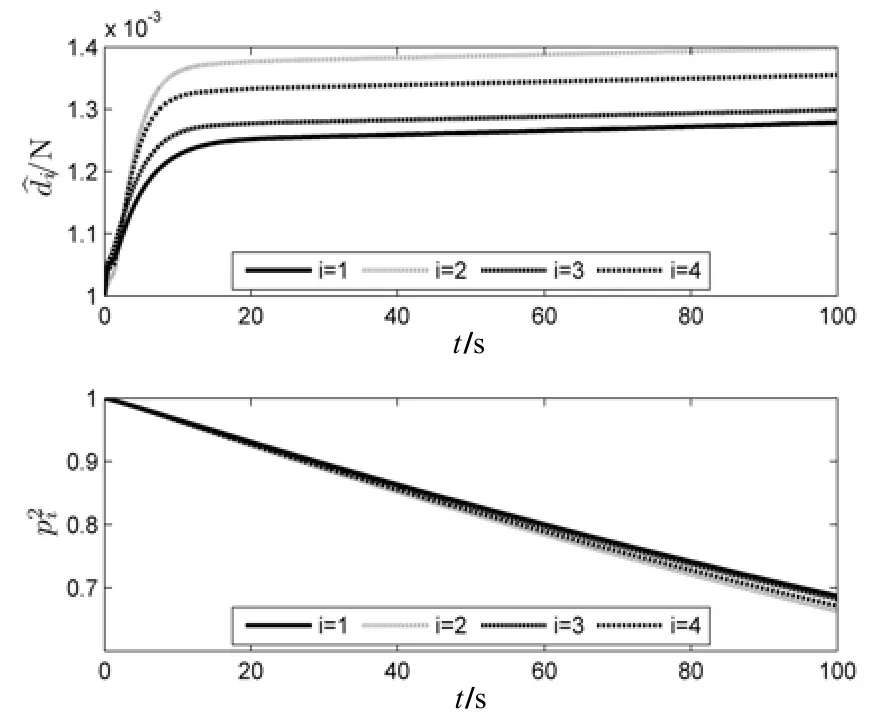
图5 自适应参数i和的变化曲线Fig.5 Adaptive parametersiand

4 结 论

针对导弹编队协同攻击问题，本文提出了鲁棒自适应编队控制策略，能够克服外部干扰和内部参数不确定性的影响，同时满足导弹编队控制的要求。对于有无通信时滞的情况，均给出了系统渐近稳定所需要的条件。与传统的滑模控制等非连续鲁棒控制不同的是，本文提出的控制器是连续的，更便于导弹编队系统的实现。数值仿真验证了文中给出的控制方法的有效性，各编队导弹稳态误差较小，能够满足导弹编队飞行控制精度要求。在仅有部分导弹获取期望信息的情况下，设计鲁棒自适应队形控制策略，是今后进一步需要做的工作。

（References）：

[1] 张磊, 方洋旺, 毛东辉, 等. 导弹协同攻击编队自适应滑模控制器设计[J]. 宇航学报, 2014, 35(6): 700-707. Zhang L, Fang Y W, Mao D H, et al. Adaptive slidingmode controller design for missile cooperative engagement[J]. Journal of Astronautics, 2014, 35(6): 700-707.

[2] Scharf D P, Hadaegh F Y, Ploen S R. A Survey of spacecraft formation flying guidance and control (Part II): control[C]//Proceedings of the 2004 American Control Conference. Boston, Massachusetts, 2004, 2976-2985.

[3] Lawton J R, Beard R W, Young B J. A Decentralized approach to formation maneuvers[J]. IEEE Transactions on Robotics and Automation, 2003, 19(6): 933-941.

[4] Consolini L, Morbidi F, Prattichizzo D, et al. Leaderfollower formation control of non-holonomic mobile robots[J]. Automatica, 2008, 44(3): 1343-1349.

[5] De Q M, Kapila V, Yan Q. Adaptive nonlinear control of multiple spacecraft formation flying[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(3): 385-390.

[6] 张保群, 宋申民, 陈兴林. 考虑控制饱和的编队飞行卫星姿态协同控制[J]. 宇航学报, 2011, 32(5): 1060-1069.

Zhang B Q, Song S M, Chen X L. Attitude coordination control of formation flying satellites under control saturation[J]. Journal of Astronautics, 2011, 32(5): 1060-1069.

[7] Cui N G, Wei C Z, Guo J F, et al. Research on missile formation control system[C]//IEEE International Conference on Mechatronics and Automation. Changchun, 2009.

[8] 王晓芳, 郑艺裕, 林海. 导弹编队飞行控制方法研究[J]. 北京理工大学学报, 2014, 34(12): 1272-1277. Wang X F, Zheng Y Y, Lin H. Control method for missile formation flight[J]. Transactions of Beijing Institute of Technology, 2014, 34(12): 1272-1277.

[9] Wang X F, Zheng Y Y, Lin H. Integrated guidance and control law for cooperative attack of multiple missiles[J]. Aerospace Science and Technology, 2015, 42: 1-11.

[10] Wang L, He F H, Yao Y, et al. Guidance law design for two flight vehicles cooperative interception[C]//AIAA Guidance, Navigation and Control Conference, 2015: 1-11.

[11] Edward D, Qu Z H. Optimal design of cooperative guidance law for simultaneous strike[C]//53rd IEEE Conference on Decision and Control. California, USA, 2014: 988-993.

[12] Zhao S Y, Zhou R. Cooperative guidance for multimissile salvo attack[J]. Chinese Journal of Aeronautics, 2008, 21(6): 533-539.

[13] Jeon I, Lee J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280.

[14] 张友安, 马国欣, 王兴平. 多导弹时间协同制导：一种领弹-被领弹策略[J]. 航空学报, 2009, 30(6): 1109-1118. Zhang Y A, Ma G X, Wang X P. Time cooperative guidance for multi-missiles: a leader-follower strategy[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1109-1118.

[15] 韦常柱, 郭继峰, 崔乃刚. 导弹协同作战编队队形最优保持控制器设计[J].宇航学报, 2010, 31(4): 1043-1050 . Wei C Z, Guo J F, Cui N G. Research on the missile formation keeping optimal control for cooperative engagement[J]. Journal of Astronautics, 2010, 31(4): 1043-1050.

[16] 张磊, 方洋旺, 刁兴华, 等. 多导弹协同攻击编队非线性最优控制器设计[J]. 北京航空航天大学学报. 2014, 40(3): 401-406. Zhang L, Fang Y W, Diao X H, et al. Design of nonlinear optimal controller for multi-missile formation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(3): 401-406.

[17] Wang H L. Passivity based synchronization for networked robotic systems with uncertain kinematics and dynamics [J]. Automatica, 2013, 49(3): 755-761.

[18] Wallsgrove R J, Akella M R. Globally stabilizing saturated attitude control in the presence of bounded unknown disturbances[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(5): 957-963.

[19] Khalil H K. Nonlinear systems[M]. Upper Saddle River, New Jersey: Prentice-Hall, 2002.

Distributed robust adaptive control for missile cooperative engagement within formation

ZHOU Hui-bo1,2, SONG Shen-min2, ZHENG Zhong2
(1. School of Mathematical Sciences, Harbin Normal University, Harbin 150009, China; 2. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China)

The problem of robust adaptive cooperative tracking control of missile formation is investigated under directed communication topology. According to the formation tracking, external disturbance and model uncertainties in the system of missile formation, a robust adaptive formation control scheme with directed communication topology is proposed by selecting an auxiliary variable including position tracking error and velocity tracking error. The adaptive laws are presented to estimate the unknown parameters, and the asymptotical stability of closed-loop system is analyzed using Lyapunov stability theory. Furthermore, the conditions to satisfy the asymptotical stability of the system are given for the case of communication delays. Being different from traditional robust controls such as sliding mode control, the designed robust adaptive controller is continuous, so it is convenient to be implemented in the system of missile formation. Simulation results show that the tracking error and the keeping error of the formation are less than 0.03 m and 0.07 m, respectively, so the designed controller can achieve high-precision formation tracking control.

missile formation; cooperative engagement; communication delay; robust adaptive control; directed graph

V448.133

A

1005-6734(2015)04-0516-06

10.13695/j.cnki.12-1222/o3.2015.04.018

2015-02-26；

2015-06-12

国家自然科学基金（61174037）；国家自然科学基金创新群体项目（61021002）；上海航天科技创新基金项目（SAST201402）；航空科学基金项目（20140177002）

周慧波（1977—），女，博士研究生，研究方向为飞行器制导与控制。E-mail：zhouhb0306@sina.com

联 系 人：宋申民（1968—）男，教授，博士生导师，研究方向为非线性系统的稳定性分析、鲁棒控制、导弹制导与飞行器控制。E-mail：songshenmin@hit.edu.cn