伸缩式鸭舵二维修正策略和修正能力

谢克峰，张 合，唐玉发，龙 礼

（1. 南京理工大学 机械工程学院，南京 210094；2. 南京理工大学 智能弹药技术国防重点学科实验室，南京 210094；3. 南京工程学院 自动化学院，南京 210013）

伸缩式鸭舵二维修正策略和修正能力

谢克峰1,2，张 合1,2，唐玉发1,2，龙 礼3

（1. 南京理工大学 机械工程学院，南京 210094；2. 南京理工大学 智能弹药技术国防重点学科实验室，南京 210094；3. 南京工程学院 自动化学院，南京 210013）

为了提高小口径火箭弹的射击精度，提出了一种伸缩式鸭舵修正方案。通过分析鸭舵的修正力建立了弹道修正模型，分析了鸭舵修正的最佳起始点和启动角度，通过工程计算和CFD仿真对伸缩鸭舵的气动力系数和修正力进行了数值仿真。最后通过风洞实验验证了伸缩式鸭舵的二维修正能力，鸭舵舵片在1.5 Ma来流作用下产生的修正控制力为22 N，与数值仿真相吻合。该结果对伸缩式鸭舵的飞行实验和制导化工程应用具有重要意义。

伸缩鸭舵；数值仿真；风洞实验；修正能力

弹道修正技术是目前发展最快的提高弹箭准确度的一种技术[1]，其中修正执行机构是实现弹道修正的关键技术。二维弹道修正由于能实现距离和方向上的双重修正，大幅度提高弹箭命中率，因而在修正技术中成为主要研究对象。美国某公司的精确制导组件PGK通过固定鸭舵和火箭弹的双旋控制来实现二维修正，其圆概率误差小于30 m[2]。德国的增强型弹道修正（CORECT）模块[3]技术采用小火箭脉冲推理修正，结构简单，成本低廉，其圆概率误差小于50 m。

二维弹道修正技术主要分为鸭舵式和脉冲式，鸭舵式能够实现多次修正，并且容易实现对现存弹进行改装，从而成为近年国内外研究的重点。文献[4-6]对隔转控制固定鸭舵进行了研究，提出了适合简易制导弹药的系统模型，对固定鸭舵的气动特性进行了仿真分析，但是滚转舵控制比较复杂，实现隔转的减旋和稳定比较困难，不适用于小口径微旋火箭弹；文献[7-8]对一种伸缩式电磁舵机进行了一定研究，针对扭矩特性和输出特性进行了优化。本文基于小口径火箭弹修正的需要，提出了一种伸缩式鸭舵控制方法，通过GPS测量弹道偏差，控制鸭舵在合适位置伸出与收缩，来实现弹道的二维修正。

1 伸缩鸭舵修正原理

在弹丸飞行过程中，通过GPS测量实际弹道，与理想弹道比较产生弹道偏差，控制系统控制鸭舵在某一合适角度打出，产生合适修正力后并控制鸭舵收回。鸭舵可在微旋弹丸的任意角度完全伸出，从而鸭舵产生的修正力可以在滚转范围内指向任何方向，因此实现弹道的二维修正。而舵片完全伸出所提供的力一方面可以提供弹丸飞行的升力，另一方面由于力的作用点并不在弹丸质心处，因此会对弹体产生一个控制力矩。因此舵片的控制力一方面对弹体施以一定的升力，另一方面对弹体产生的控制力矩使整个弹体的攻角增大，进而提高全弹的升力达到改变弹丸质心运动轨迹的效果。

将一对完全伸出状态的舵片置于弹体坐标系内，如图1所示。因攻角1δ、2δ均是小量，得到舵面瞬时控制力Fc在弹体坐标下的分量为

式中，SD为舵片的特征面积，为舵面的阻力系统导数，为舵面的升力系统导数，δc为舵片的偏角。

图1 鸭舵控制力示意图Fig.1 Canards control force schematic diagram

舵面瞬时控制力Fc在速度坐标下的分量为

在忽略地球自转的影响，即不考虑科氏惯性力的前提下，将上述鸭舵控制力代入到弹箭的运动方程中，便可得到火箭弹6自由度弹道修正模型。

2 最佳修正起始点与起控角度

2.1 最佳修正起始点

火箭弹在主动段容易受到发射时的初始扰动、推力偏心、动静不平衡度及阵风等干扰因素的影响，这也是造成无控火箭弹落点散布较大的直接原因。因此选择在弹道下降段（含弹道顶点）进行弹道修正是最常用的方法。

图2（a）是某无控火箭弹在弹道平面内的运动轨迹。点O为弹道起点，即火箭发动机开始点火的位置；点K为主动段末端，即火箭发动机结束工作的位置；点S为弹道顶点；点N为火箭弹的速度极小值点；点C为弹着点，即落点。从原点O到落点C的距离X表示射程。KS与SC中的任一点都可能是伸缩式鸭舵执行修正的启控点[9]。

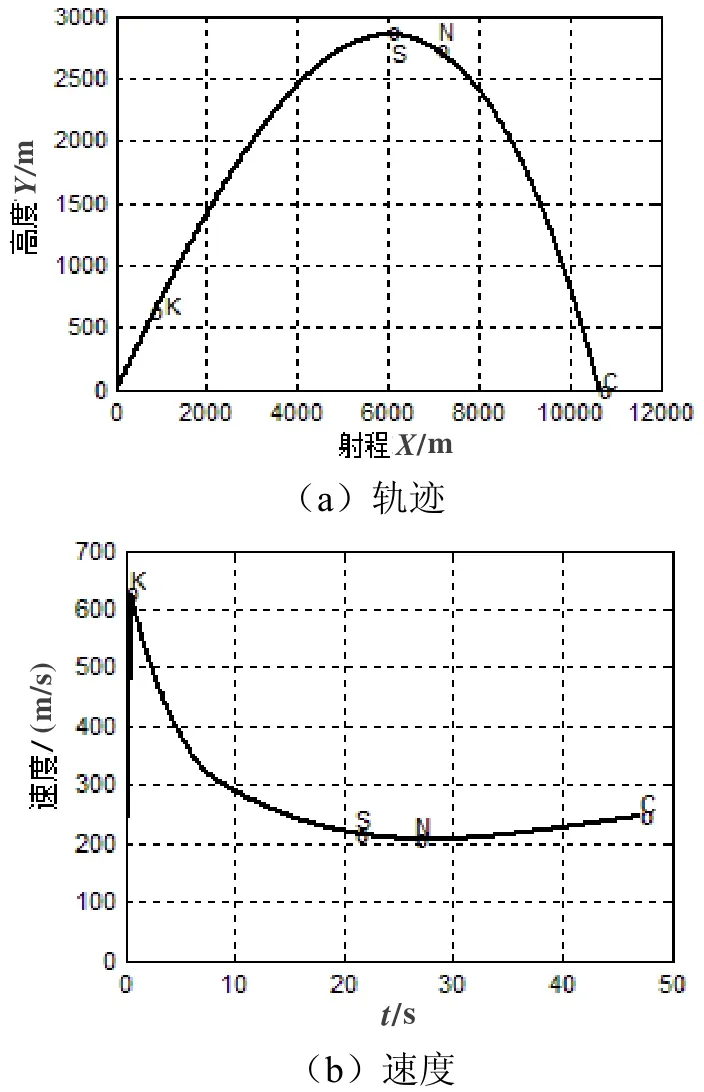
图2 某火箭弹弹道曲线与速度Fig.2 A rocket’s trajectory curve and speed

图2（b）是某无控火箭弹的质心运动速度沿全弹道变化曲线图。在主动段内推力加速度比阻力加速度ax及重力加速度gsinθ大得多，速度快速增大，在火箭发动机结束工作的K点时速度达到最大；在弹道的升弧段KS上，阻力加速度ax和重力加速度gsinθ起主要作用，且与弹丸速度方向始终相反，故速度减小；在弹道顶点S处，θs=0，gsinθ=0，阻力加速度ax不等于零，故速度继续减小；过弹道顶点S后，gsinθ的方向与阻力加速度ax的方向相反，即由于重力因素导致速度增加，随着θ的增大，到某一时刻，达到ax=gsinθ，这时速度不再减小，即在N点速度达到最小值；过N点后，通常情况是gsinθ＞ax，故使速度增大。可以看出火箭弹在通过弹道顶点S后直至落地前速度先会达到极小值再缓缓增加，因此在此范围内进行弹道修正可以减小对控制力与控制力矩的要求。

2.2 最佳起控角度

由于所研究的弹丸在空中不停地微旋转，伸缩式鸭舵在不同的弹体飞行速度下伸出与收回舵片所用的时间不尽相同。为了使伸缩式鸭舵最大化地提供修正力，弹载计算机必须计算出合适的启控角度。

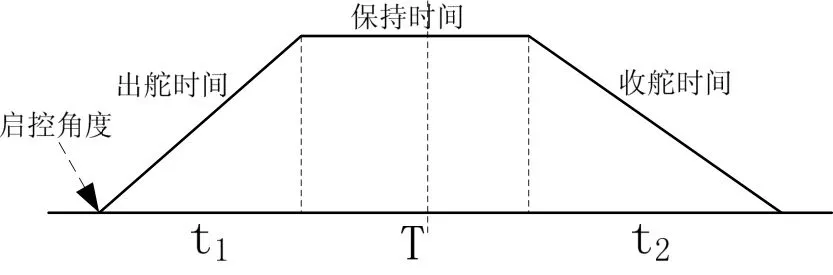
图3 启控角度与鸭舵伸出收回时间Fig.3 Starting time and extending and recovering time of canard

弹丸的转速可以根据固定周期内地磁传感器连续发出的两组姿态角度数据进行解算得出，假设其固定周期为T1，两次解算的滚转角分别为1θ、2θ，则弹丸的转速n为

假设伸缩式鸭舵舵片完全伸出所用时间为t1，舵片完全收回所用时间为t2，舵片在空气中停留的时间为T，则伸缩式鸭舵能提供最大修正力的修正条件为

舵片保持时间：

假设舵片的伸出与收回均是线性的，为了保证舵片在修正角度Φ附近产生修正力全部为所需修正力，则要求舵片在伸出与收回过程中产生的反向修正力相互消除，即修正角度Φ即处于梯形面积的一半位置处，如图3所示。

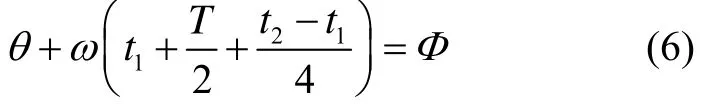
因此可以得到启控滚转角θ：

3 伸缩鸭舵气动力仿真分析

理论计算以往主要采用的是经验公式、工程计算方法及数值计算方法。随着研究水平及手段的不断提高，经验公式计算弹丸气动力系统已难以适应科研工作的需要。工程计算方法基于空气动力学理论进行计算机求解，目前仍是外弹道研究中获取弹丸空气动力参数最广泛使用的计算方法。数值计算方法完全是基于空气动力学的基本方程，建立起气流绕流飞行体的流场数学力学模型（如N-S方程），求出作用在弹丸上的空气动力及相应的系数。数值计算方法随着计算机技术而迅速发展，此方法较优越并逐步被广泛应用[10]。

3.1 工程计算

根据气动力系数的工程计算方法，得到舵片的升力和阻力系数为

根据上述气动参数模型得matlab曲线到如图4所示曲线。

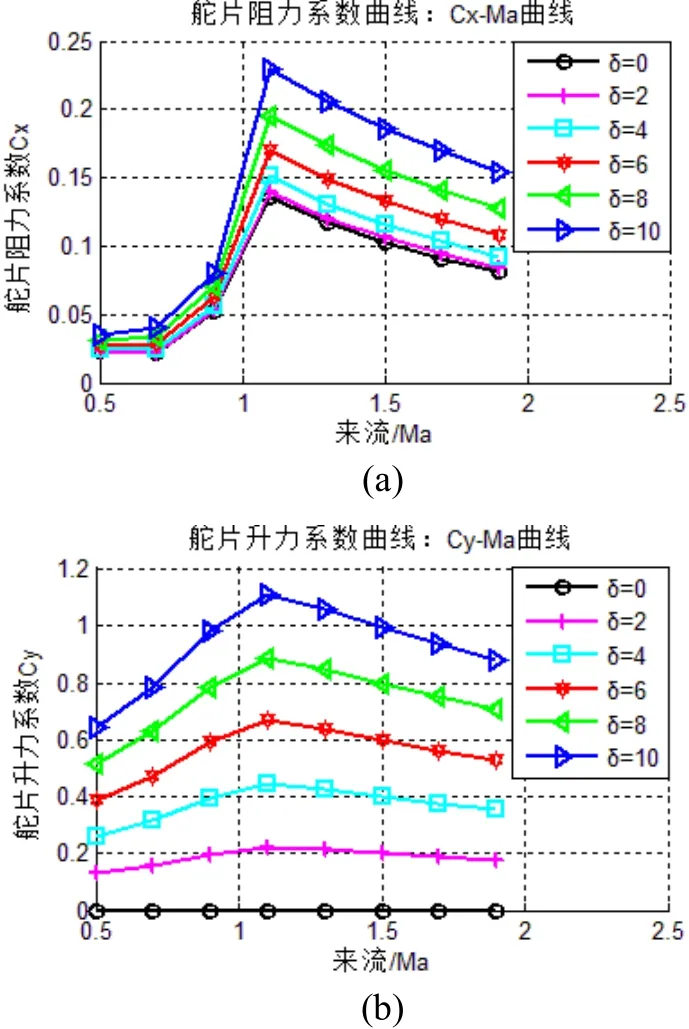
图4 不同攻角与马赫数下舵片阻力与升力系数曲线Fig.4 Drag and lift coefficient curves of canard in different attack angles and mach numbers

图4为单独舵片在不同攻角下的升力系数与阻力系数曲线。从图4中可以看出，在亚音速阶段，因舵片的阻力主要由摩阻与涡阻组成的型阻产生，在此阶段阻力系数变化较小，但在跨音速及超音速阶段由于激波的存在，波阻起到主要作用，随着激波的程度加深，波阻力增加，相应地舵片阻力系数变化较大。随着马赫数的增大，激波逐渐附体，阻力曲线随之下降，而升力系数曲线随攻角的增大而增大，随来流的增大先增大后减小。

3.2 物理模型

在不改变常规火箭弹的结构基础上在其弹身上加装修正执行机构—伸缩式鸭舵，与原型火箭弹结构一样为尖拱—圆柱旋成体，其模型如图5所示。

图5 弹体计算模型图Fig.5 Calculation model of projectile

3.3 网络划分及边界条件

将伸缩式鸭舵的舵片单独定义成WALL边界条件。计算区域划分为两块区域：小块为弹体附近的流场，在径向延伸到12D，轴向延伸到29D；大块在径向延伸到40D，轴向延伸到80D，网格总数约185万，壁面附近最小网格间距为1×10-5D。网格划分如图6和图7所示。

图6 外流场网格划分示意图Fig.6 Schematic of drain field meshing

图7 弹体网格划分示意图Fig.7 Schematic of projectile meshing

在边界条件的设置上，采取密度基耦合显式求解器进行求解可压缩流动，对来流采用远场边界条件，在物面上采用粘性边界条件，即无滑移边界条件[11]：

式中：ui(i=1,2,3)为沿坐标方向的三个速度分量，p为压力，ρ为密度，n为法线方向。远场边界采用自由流条件，入流边界利用来流值，出流边界利用内场值外推得到。

3.4 仿真结果及分析

得到舵片的气动参数如图8所示。从图8中可以看出：在相同的马赫数条件下单独舵片的升力系数与阻力系数都与攻角成正比；在攻角一定时，随着马赫数的增加，升力系数与阻力系数均是先增大后减小，且在跨音速1.2 Ma附近时升力系数与阻力系数都达到最大值。

图8 单独舵片阻力系数与升力系数Fig.8 Lift and drag coefficients of single canard

在伸缩式鸭舵提供舵片的固定舵偏角为δc=+8°的前提下，单独舵片所能产生的升阻比约为3.85左右，在已知升力系数前提下，根据升力计算公式Ry=ρυ2SCy2得到单独舵片在不同马赫数下的所能提供的升力值，如图9所示。

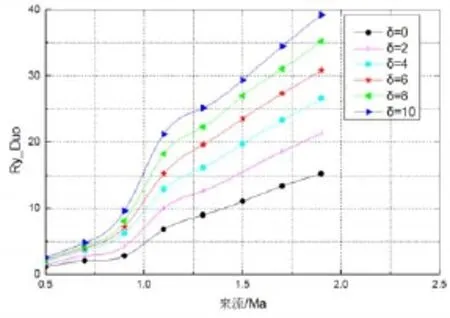
图9 单独舵片的升力变化曲线Fig.9 Lift curves of single canard

攻角不变时，马赫数越大，伸缩鸭舵产生的修正力越大；马赫数不变时，攻角越大，伸缩鸭舵产生的修正力越大。在0°攻角时，单独舵片在1 Ma能提供约5 N的升力值，在1.5 Ma能提供约11 N的升力值，在1.9 Ma能提供约15 N的升力值。

4 风洞实验验证

风洞是一种既可以产生模拟真实大气情况，又可以对气流进行控制的试验装置，其应用范围非常广泛[12]。为了验证本文所研究的伸缩式鸭舵能否在实弹环境中稳定可靠地执行修正功能，也需要对其模型进行吹风实验以便对其二维修正能力进行验证，为其后续实弹飞行试验提供重要的实验支撑。风洞实验如图10所示。

图10 风洞实验安装图Fig.10 Installation diagram of the wind tunnel test

将方案弹道与实际飞行弹道的偏差信息存储于弹载计算机中，弹尾翼在受到风洞气流的作用下产生导转力矩驱动弹体顺时针自由转动。在修正过程中弹载控制器会将工作过程中的状态及执行等标志存储于弹载铁电存储器。在既定偏差的情况下，弹载计算机连续控制鸭舵动作，舵片动作瞬间示意图及各修正标志校验图如图11所示。

图11 方案偏差与执行偏差校验及对应滚转角Fig.11 Deviation calibration and the corresponding roll angle

图11为修正过程中记录的方案偏差与执行偏差标志校验图和鸭舵执行指令时即其动作时的滚转角。从图11上图可以看到：弹载计算机首先读取存储于弹内的偏差信息，以红色虚线表示；而后弹载计算机判定偏差的有效性，即是否需要修正后，在合适的滚转姿态执行此偏差所对应的指令信息，图中以黑色实线表示。实验结果表明，伸缩鸭舵能够按照预定弹道偏差进行动作。

对鸭舵在风洞条件下舵片产生的修正力进行测量。将鸭舵分别固定于0°、90°、180°、270°的滚转角位置，对舵片未伸出时的普通弹丸与鸭舵伸出时弹道修正弹分别进行动态压力测量实验，试验结果列于表1与表2中。

上述传感器的压力值并不是舵片伸出时产生的修正控制力，因为修正力、重力及传感器的支持力构成力矩平衡，根据力矩平衡原理，

式中： Fd为综合修正控制力，ld为修正力作用点距转动副支点的距离，G为样弹的重力，lG为重心距转动副支点的距离，Fs为不同位置相应传感器的压力值，l为传感器作用点距转动副支点的距离。

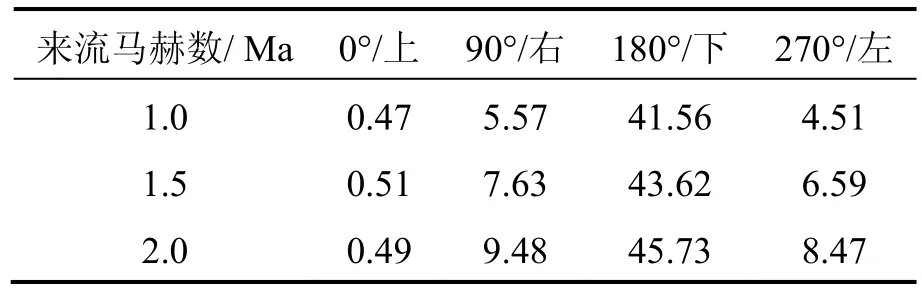
表1 普通弹丸（舵片未伸出）的压力值Tab.1 Pressure of projectile (without canard) N

表2 修正弹（舵片已伸出）的压力值Tab.2 Pressure of correction projectile (with canard) N

将表1与表2表中的压力数据分别代入式(7)可以得不同滚转位置不同样式的修正控制力，如表3所示。

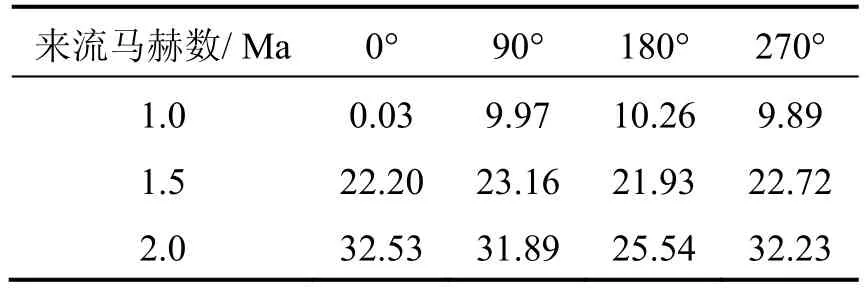
表3 舵片产生的修正控制力Tab.3 Control force of correction canard N

从表中其他数据可以看出：单独舵片（一对）在1 Ma的来流作用下可以产生约10 N的修正控制力；而在1.5 Ma的来流作用下可以产生约22 N的修正控制力；在2 Ma的来流作用下可以产生约32 N的修正控制力。实验结果与前文仿真结果基本一致，验证了前文仿真的正确性，同时也验证了伸缩鸭舵的修正能力。

5 结 论

本文提出了伸缩鸭舵修正方法，分析了鸭舵修正原理并建立了6自由度弹道修正模型，通过CFD仿真分析了修正弹的气动参数，并推导了鸭舵的修正力。风洞实验结果表明，伸缩鸭舵是一种可行的修正方法，与仿真结果一致，在1.5 Ma的来流作用下，能够产生22 N的修正力，为伸缩鸭舵修正的飞行实验和制导化工程应用提供了一定基础。

[1] 于勃彪, 严平. 弹道修正弹药现状及关键技术[J]. 四川兵工学报, 2011, 32(4): 37-43. Yu Bo-biao, Yan Ping. The actuality of ammunition for ballistic trajectory and its key technology[J]. Journal of Sichuan Ordnance, 2011, 32(4): 37-43.

[2] Burke P, Pergolizzi T. XM1156 precision guidance kit (PGK) overview[C]//The 53rd Annual Fuze Conference. 2009: 5-20.

[3] Thomas D, Kreuzer W G, John N. Rocket Trajectory Correction using Strap-on GPS Guided Thrusters[EB/OL]. [2002-04-16.]http://www.dtic.mil/ndia/2002gun/jollife.pdf

[4] Cheng Jie, Wang Xiao-ming, Yu Ji-yan. On the response of spin stabilized projectile to side force by angular motion and impact[C]//27th International Symposium on Ballistics. Freiburg, Germany, 2013: 225-232.

[5] 王毅, 宋卫东, 佟德飞. 固定鸭舵式弹道修正弹二体系统建模[J]. 弹道学报, 2014, 26(4): 36-41. Wang Yi, Song Wei-dong, Tong De-fei. Modeling of two-rigid-body system for trajectory correction projectile with fixed-canard[J]. Journal of Ballistics, 2014, 26(4): 36-41.

[6] Wernert P. Stability analysis for canard guided dual-spin stabilized projectiles[C]//Proceedings of AIAA Atmospheric Flight Mechanics Conference. Chicago, 2009: 1-24.

[7] 唐玉发, 张合, 马少杰, 等. 制导用伸缩式电磁舵机输出特性优化[J]. 中国惯性技术学报, 2013, 21(5): 692-696. Tang Yu-fa, Zhang He, Ma Shao-jie, et al. Optimization for output characteristics of telescopic electromagnetic actuator for guidance[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 692-696.

[8] 徐国泰, 马少杰, 唐玉发. 双向转角电磁铁输出扭矩特性仿真分析[J]. 现代电子技术, 2012, 35(21): 145-148. Xu Guo-tai, Ma Shao-jie, Tang Yu-fa. Simulation analysis of output torque of two-way corner electromagnet[J]. Modern Electronics Technique, 2012, 35(21): 145-148.

[9] Hanson J M, Beard B B. Applying Monte Carlo simulation to launch vehicle design and requirements verification[J]. Journal of Spacecraft and Rockets, 2012, 49(1): 136-144.

[10] 洪黎, 张合, 唐玉发, 徐国泰. 简易制导火箭弹鸭舵气动特性对弹道的影响[J]. 南京理工大学学报, 2014, 38(3): 380-384. Hong Li, Zhang He, Tang Yu-fa, Xu Guo-tai. Influences of aerodynamic characteristics of canard rudders for simple guided rockets on trajectories[J]. Journal of System Simulation, 2014, 38(3): 380-384.

[11] 武频, 赵润祥, 郭锡福. 双组尾翼弹气动特性计算与分析[J]. 空气动力学学报, 2002, 20(4): 411-415. Wu Pin, Zhao Run-xiang, Guo Xi-fu. Aerodynamic character calculation and analysis of two sets of empennages bullet[J]. Acta Aerodynamica Sinica, 2002, 20(4): 411-415.

[12] Tang Yufa, Zhang He, Long Li. Attitude angle measurement technique based on the three-dimensional accelerometer[C]//2013 2nd International Conference on Measurement, Instrumentation and Automation. Guilin, China, 2013: 152-156.

Two-dimension correction strategy and capability for retractable canard

XIE Ke-feng1,2, ZHANG He1,2, TANG Yu-fa1,2, LONG Li3
(1. Nanjing University of Science and Technology, School of Mechanical Engineering, Nanjing 210094, China; 2. Ministerial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing 210094, China; 3. Dept. of Automation, Nanjing Institute of Technology, Nanjing 210013, China)

To improve the concentration of small caliber rockets, a correction method based on retractable canard was presented. By analyzing the correction force of retractable canard, the 6-DOF trajectory correction models were established. The best starting point and starting angle for correction of canard were analyzed. Numerical simulation for aerodynamic coefficients and correction force of correction projectiles with retractable canard was made by engineering calculation and CFD simulation. Two-dimension correction capability of retractable canard is verified by wind tunnel experiments, which show that the correction force by retractable canard is 22 N at 1.5 Ma, and is conformed to that of the numerical simulation. This result is of great importance for the flight experiment and the guided engineering applications of retractable canards.

retractable canard; numerical simulation; wind tunnel experiments; correction capability

TJ430.1

A

1005-6734(2015)04-0477-06

10.13695/j.cnki.12-1222/o3.2015.04.011

2015-05-08；

2015-07-19

国家自然科学基金（60908037）

谢克峰（1988—），男，博士研究生，从事引信智能化与灵巧化技术研究。E-mail：xiekefeng.ok@163.com

联 系 人：张合（1957—），男，教授，博士生导师。E-mail：hezhangz@mail.njust.edu.cn