基于等效变预载法的静电加速度计闭环零点调节

刘 爽，刘云峰，韩丰田，徐 哲，董景新

（清华大学 精密仪器系 高精度惯性仪表及系统技术教育部重点实验室，北京 100084）

基于等效变预载法的静电加速度计闭环零点调节

刘 爽，刘云峰，韩丰田，徐 哲，董景新

（清华大学 精密仪器系 高精度惯性仪表及系统技术教育部重点实验室，北京 100084）

闭环零点位置对差动电容式静电加速度计性能具有重要影响，闭环零点偏离机械零点会增大标度因子非线性。为精确调节闭环零点，提出了一种等效变预载闭环零点调节方法，能够在预载和反馈电压不对称情况下实现闭环零点位置的精确辨识和调节。利用静电加速度计原理样机测试了闭环零点调节前后的系统非线性特性，实验结果表明采用上述方法进行闭环零点调节后，表征标度因子非线性的二次项系数由-1.7×10-7降低为-3.3×10-8,验证了上述方法的有效性。

非线性；变预载；闭环零点位置；静电加速度计

空间应用的高精度的静电加速度计依靠可控的静电力将敏感质量悬浮起来，具有分辨率高、量程小、频带窄等特点，适合测量缓变的微弱加速度，其分辨率可达10-7～10-14g/Hz1/2（0.1 mHz～0.1 Hz），可应用在卫星精密定轨、重力场测量及等效原理验证等空间应用领域[1-3]。

静电加速度计具有极高分辨率，因此要求其具有极低标度因子非线性。闭环工作时，电容式静电加速度计闭环零点位置偏离机械零点（电极框几何中心）是造成标度因子非线性的主要因素[4-5]，使敏感质量工作在机械零点可以降低标度因子非线性。此外闭环零点位置还会影响标度因数和零偏，因此有必要对静电加速度计闭环零点位置进行精确测量和调节。

一般电容式静电加速度计可采用翻滚法[6-7]和变预载法调整闭环零点位置[4]。静电加速度计水平方向量程远小于1g，不适用翻滚法。范[4]等提出的变预载闭环零点调节方法在MEMS电容式静电加速度计上得到了很好的应用，但直接应用在高精度的静电加速度计上存在很大误差，原因是该方法未考虑预载和反馈电压不对称情况带来误差。敏感质量与极板标称间隙为60 μm，要实现纳米级闭环零点位置调节必须采取精确的调节方法，因此本文提出基于等效电压的变预载闭环零点调节方法，解决了预载和反馈电压不对称情况下闭环零点精确调节问题。在加速度计量程内任意恒定加速度输入情况下，仅需几步即可将敏感质量调节到机械零点纳米级误差范围之内。

1 系统组成及工作原理

静电加速度计系统如图1所示，由表头结构、电容检测电路、DSP控制电路及高压反馈电路组成。表头由敏感质量和电极框构成6对差动电容（Y1和Y2连接，X1和X4连接），利用可控的静电力将敏感质量悬浮在电极框中，实现3个线加速度和3个角加速度的6自由度控制和测量[8]。

图1 静电加速度计工作原理图Fig.1 Schematic diagram of electrostatic accelerometer

1.1 闭环工作原理

以Y轴为例，位移检测电路输出端有如下电压关系：

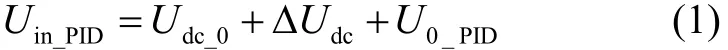
式中：Udc_0为检测电路零偏，ΔUdc为表头差动电容引起的检测电路输出，二者构成检测电路输出电压Udc；U0_PID为PID校正零点调节电压；Uin_PID为PID校正网络输入电压。PID校正作用使Uin_PID近似为零。

假设检测电路无零偏（Udc_0=0），则敏感质量闭环零点位置位于机械零点，即Δx=0，且未加校正电压（U0_PID=0）时，当外界加速度引起质量块位置偏移Δx，与上、下电极板产生差动电容ΔC，经过检测电路转化成差动电压ΔUdc，经过PID控制电路生成控制电压vb，再经过反馈高压电路在上、下极板产生±Vb反馈电压，从而与预载电压Vr一起生成静电力Fe拉动敏感质量块回到初始位置，此时ΔC=0，因此ΔUdc=0。PID中积分器作用维持输出控制电压vb产生静电力与外界力平衡，此时反馈电压与外界加速度成线性关系。

1.2 系统受力分析

如图1示，假设闭环零点相对机械零点向下偏移Δx，敏感质量所受合静电力表示为[9]

式中：εr为相对介电常数，ε0为真空介电常数，A为电极板面积，Vr1、Vr2分别为上、下极板预载电压，Vb1、Vb2分别为上、下极板反馈电压，Vs为高频激励电压，且有为标称间距。

理想情况下有Vr1=Vr2=Vr，Vb1=-Vb2=Vb，则Fe可表示为

式中：FeL表示直流分量，FeH表示交流分量。由式(2)可得到FeL和FeH表达式如下：

实际应用中，激励频率远远高于加速度计工作带宽，因此高频分量FeH可忽略，则静电力表达式简化为Fe=FeL。在静态闭环状态下，静电力Fe总是与其他施加到质量块上的外力平衡，即

因此有

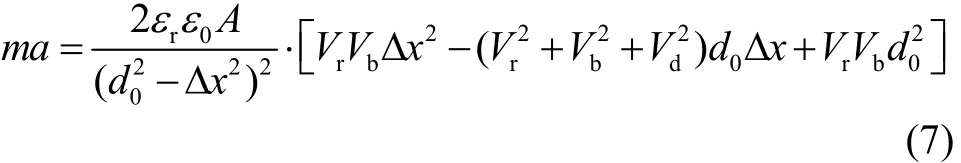
若闭环零点位置向上偏移Δx（如图2），可将式(7)中Δx换成-Δx。为此将Δx统一用x表示，规定其向上偏移为正，即与静电力合力方向相同为正，反之为负。

由式(7)得：

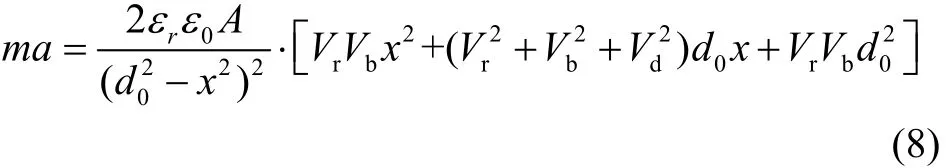
图2 闭环零点向上偏移Fig.2 Upward offset of the close-loop equilibrium position

当x=0时，有：

此时反馈电压与输入加速度成线性关系。

由于检测电路不对称通常会存在零偏（Udc_0≠0），PID控制作用仍然是使得Uin_PID=0，最终结果是产生反馈电压，生成静电力拉动敏感质量块运动，使得质量块偏移中心位置位移为x0，产生差动电容ΔC0，进而使得检测电路产生差动变化电压ΔUdc与Udc_0相抵消，以保证Uin_PID=0。显然此时质量块已经偏离机械零点，即产生闭环零点位置偏移，造成标度因子非线性。闭环零点偏移x0与Udc_0关系可表示为[10]

式中：KΔC→Udc为检测电路标度因数，C0为标称电容。由式(1)和式(10)可知，调节U0_PID可以调节x0大小，即调节闭环零点位置，当使得U0_PID=-Udc_0，则敏感质量便调节到机械零点。关键是如何精确地获得U0_PID或x0值。

2 变预载闭环零点调节原理

采用变预载闭环零点调节方法可以有效解决具有机械梁的电容式加速度计闭环零点调节问题，可将其思想借鉴到无梁的静电加速度计上。但由于静电加速度计采用的预载和反馈电压高，电压不对称明显，直接应用该方法会有很大误差。因此本文在该方法基础上提出基于等效预载和等效反馈的变预载闭环零点调节方法（简称等效变预载闭环零点调节方法），可以有效解决电压不对称造成闭环零点调节误差问题。首先需要简单介绍下变预载闭环零点调节原理[4]。

当x=0时，由式(9)可得

可见，在外界输入加速度不变情况下，Vr×Vb为定值，当Vr变化时，Vb也随之变化。

当x≠0时，由式(8)得ma=f(Vr，Vb，x)，即Vr和Vb与x有关，当x不变时，给定Vr，可唯一确定Vb值。将式(8)做如下变换：

在外界输入加速度不变情况下，改变一次预载电压前、后可得到两组数据（Vr_a, Vb_a）和（Vr_b, Vb_b），代入式(12)中可得式(13)(14)，注意到，若消除反馈对检测电路的耦合，则变预载过程中不会引起闭环零点位置的变化[10]。

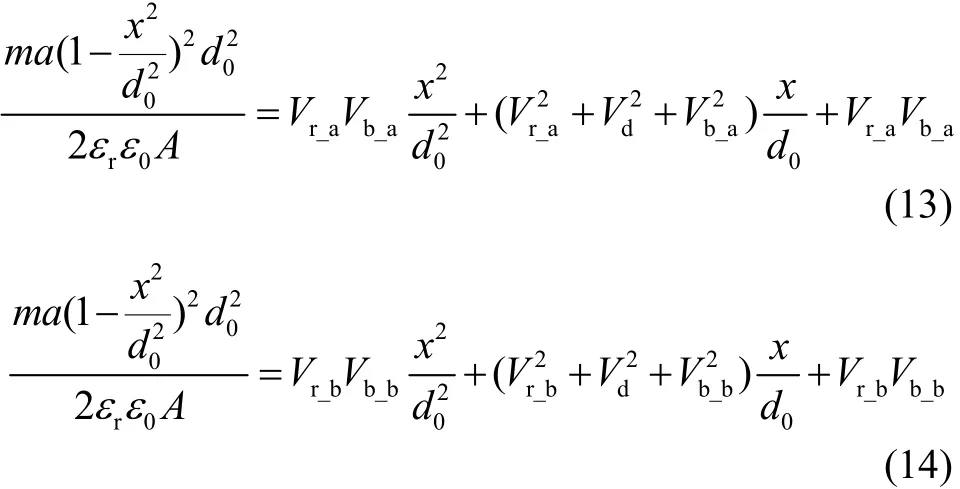
将式(13)减去式(14)，可以得到

由式(15)可知，给定两组预载电压和反馈电压，便可得到以x/d0为未知数的一元二次方程，解方程得到两个解，绝对值小于1的那个解就是当前闭环零点相对位置，其值为正说明x与静电力方向相同，反之与静电力方向相反。将这个解代入到式(13)，得

接下来通过基于LabVIEW编写的静电加速度计控制程序，逐渐改变DSP控制算法中PID校正零点调节电压U0_PID，即可调节敏感质量闭环零点位置，同时相应的Vb值跟随变化。测量反馈电压值，当其值为计算得到的反馈电压值Vb_0时，敏感质量理论上便位于机械零点。注意实际测量的是D/A输出端的控制电压vb，因此需将Vb_0除上放大倍数K，求得vb_0。

上述推导过程基于一个重要前提：上、下极板电压对称，即Vr1=Vr2=Vr，Vb1=-Vb2=Vb；若不满足此条件，采用上述方法调节闭环零点存在很大误差，甚至得到完全错误的结果。

图3给出仿真预载和反馈存在误差情况下闭环零点调节误差。假定闭环零点位于机械零点，设定输入加速度a=1.43 mg（与后面实验一致），根据表1中表头参数，由式(11)可计算出常数C。因此在预载电压Vr_a=55 V时，得到相应反馈电压Vb_a=C/Vr_a；变预载后Vr_b=95 V，相应反馈电压Vb_b=C/Vr_b，且有Vr_b＞Vr_a＞Vb_a＞Vb_b，在两组理想预载和理想反馈电压基础上加入误差电压ΔV，按照式(15)计算出存在电压误差时得到的闭环零点位置误差，仿真结果如图3所示。

表1 Y通道参数Tab.1 Parameters for channel Y

由图3可见，预载电压和反馈电压误差对x/d0结果十分敏感，1 V电压变化最大会引起闭环零点位置1.75%的变化。若期望调节闭环零点相对偏差至10-4以下，电压不对称误差应小于0.01 V，实测电压不对称误差远大于此值。因此为解决预载和反馈电压不对称误差对环点调节精度的影响，提出等效变预载闭环零点调节方法。图3中其他误差情况仿真结果介于四条曲线之间。

图3 存在电压误差情况下闭环零点调节误差Fig.3 Different x/d0in the presence of voltage error

3 等效变预载闭环零点调节原理

由图1可知有如下电压关系：

式中，Ka、Kb为D/A输出端的控制电压vb1、vb2到上、下极板反馈电压Vb的增益，且有vb1=-vb2=vb。

由于电路参数很难做到完全对称，因此有预载电压不等，反馈电压绝对值不等，即

现定义Vrs为等效预载电压，其值为上、下极板总电压代数和的一半；Vbs为等效反馈电压，其值为实际电压减去Vrs，即

令上、下极板等效预载电压相等，即

联立式(18)(20)(21)得

令V1s、V2s分别为上、下极板做等效变换后实际总电压，有

将式(22)代入式(23)得

即做等效后不改变实际加载电压，因此不会影响加力效果，但做等效之后保证了上、下极板等效预载电压相等，等效反馈电压互为相反数，满足式(8)前提条件。

实际应用时，改变预载电压前、后可得到的两组电压(Vr1_a, Vr2_a, vb_a)和(Vr1_b, Vr2_b, vb_b)，Ka、Kb事先通过实验数据线性拟合得到。按照式(22)换算成两组等效预载和等效反馈电压(Vrs_a, Vbs_a)和(Vrs_b, Vbs_b)，代入式(15)求得闭环零点相对位置x/d0，进而按照式(16)可得到常数C。

敏感质量位于机械零点时，由式(11)得

联立式(22)和式(25)得

化简得

将Vr1_a和Vr2_a替换上式中Vr1和Vr2求解关于vb的一元二次方程，取其中唯一合理解vb_0，即为在当前预载电压下将闭环零点调节到机械零点时所需的控制电压值，接下来调节U0_PID，使得实测vb值等于vb_0，即将闭环零点调节到机械零点。

需要注意的是采用上述方法虽然将敏感质量调节到机械零点，降低了由于闭环零点偏移引起的标度因子非线性，但由于反馈通道不对称仍然存在一定的非线性，理由如下。联立式(25)(27)得

式(28)说明，即使闭环零点完全位于机械零点，由于反馈回路的不对称，加速度a与控制电压vb仍然存在非线性关系，其二次项系数与Ka、Kb平方差有关。但在保证Ka、Kb相差较小情况下，由反馈通道带来的标度因子非线性远小于由闭环零点位置偏移带来的标度因子非线性。此外，采用上述方法可对敏感质量在电极框中姿态进行精确识别和辨识，从而使敏感质量在电极框中姿态处于理想位置，便于实现闭环控制。因此采用等效法调节闭环零点位置具有实际意义。

4 实验研究

4.1 实验设置

利用静电加速度计原理样机进行实验研究，实验装置如图4所示。以Y轴为例，通过基于LabVIEW的实时控制程序，在静电加速度计正常悬浮状态下改变预载电压Vr，通过D/A端口采集控制电压vb。

通过实验测量闭环零点调节前后Y轴二次项系数来验证上述调节方法的有效性。调整测试平台倾角，通过电子水平仪记录平台偏转角度α，则水平Y方向输入加速度可表示为a=g×α，同时记录Y向控制vb值，将vb乘上放大倍数40，得到反馈电压Vb。做出一系列a和Vb数据点，采用最小二乘法进行二次曲线拟合，得到的二次项系数可反映系统标度因子非线性。

图4 实验装置框示意图Fig.4 Block diagram of experiment

4.2 实验结果及讨论

等效变预载闭环零点调节过程如下：在静电加速度计稳定悬浮状态下，测量Y向变预载前后的两组预载和控制电压值如下：(55.6343 V，53.2655 V，0.74335 V)、(94.3216 V，92.2321 V，0.41838 V)。其中已知Ka=-38.538，Kb=-38.843，根据式(22)求得两组等效预载和等效反馈电压为(54.563 V，-27.576 V)和(93.343 V，-15.143 V)，将其代入式(15)可求得此时闭环零点位置x/d0=-0.017536。根据式(16)和(27)计算在初始预载电压下将敏感质量调节到机械零位时所需控制电压vb_0=0.77533 V，接下来逐渐调整U0_PID直至vb接近vb_0(vb=0.77528 V)，此时U0_PID=-0.0872 V。再次变预载得到两组控制电压vb分别为0.77528 V和0.46252 V，结合之前的预载电压重新计算闭环零点位置，得x/d0=1.4×10-4，此时已非常接近机械零点，完成闭环零点位置调节。若不满足精度要求，重复上述过程。

若采用直接变预载法调节闭环零点位置，认为上、下极板预载电压相等。变预载前后得到两组预载和控制电压值(55 V，0.74637 V)、(95 V，0.42036 V)，按式(15)计算出x/d0=-0.00828，按照式(16)和(17)计算出vb_0=0.76142 V，接下来逐渐调整U0_PID直至vb接近vb_0(vb=0.76149 V)，此时U0_PID=-0.042 V。再次变预载得到两组控制电压(55 V，0.76149 V)、(95V，0.44195 V)，求得此时闭环零点位置为x/d0=7.714×10-4。

为验证闭环零点调节方法的有效性，分别测量未调节闭环零点、直接变预载调节及等效变预载法调节闭环零点情况下输入加速度与反馈电压关系，将得到的输入加速度a和反馈电压Vb进行二次曲线拟合，拟合得到的二次项系数K2见表2。

表2 闭环零点调节前后二次项系数K2值Tab.2 Values of K2before and after debugging

由表2拟合结果可知，采用等效变预载法闭环零点调节后，二次项降低5倍左右，验证了等效变预载闭环零点方法有效；而由于反馈通道误差，采用直接法调节闭环零点后，系统仍然存在较大标度因子非线性，说明由于反馈通道不对称采用直接法调节闭环零点位置存在较大误差，且反馈通道不对称越大，则调节误差将会越大。

此外将表头与检测电路断开，实测检测电路零偏Udc_0=0.07693 V，已知C0=17.96 pF，KΔC→Udc=0.115 V/pF，代入式(10)可得x0/d0=-0.01862。该结果与等效变预载法计算求得的闭环零点调节前位移(-0.01754)相符，而直接法求得x/d0=-0.008280，与实际情况相差较大，因此进一步验证了等效变预载闭环零点调节方法的正确性。

值得注意的是，由于反馈通道不对称使得加速度计仍然存在一定的标度因子非线性，造成K2不完全为零。因此若要进一步降低系统标度因子非线性，需要提高反馈通道对称性。

5 总 结

采用本文提出的等效变预载闭环零点调节方法，能够在预载和反馈电压不对称情况下实现闭环零点精确调节，从而有效地改善静电加速度计的标度因子非线性。该方法同样适用于有梁的MEMS电容式加速度计。此外降低反馈电压噪声、提高预载和反馈电压测量精度可进一步提高闭环零点调节精度。

（References）：

[1] Hudson D, Chhun R, Touboul P. Development of a differential accelerometer to test the equivalence principle in the microscope mission[J]. Acta Astronautica, 2005, 57(2): 341-347.

[2] Danzmann K. LISA—an ESA cornerstone mission for the detection and observation of gravitational waves[J].

[3] Touboul P, Foulon B, Christophe B, et al. CHAMP, GRACE, GOCE instruments and beyond[J]. Geodesy for Planet Earth, 2012, 136: 215-221.

[4] Fan Da, Liu Yun-feng, Han Feng-tian, et al. Identification and adjustment of the position and attitude for the electrostatic accelerometer's proof mass[J]. Sensors and Actuators A: Physical, 2012, 187: 190-193.

[5] Caixin W, Jing-xin D, Yun-feng L, et al. Nonlinearity of a closed-loop micro-accelerometer[C]//IEEE International Conference on Control Applications. 2007: 1260-1265.

[6] Dumas N, Azais F, Mailly F, et al. A novel method for test and calibration of capacitive accelerometers with a fully electrical setup[C]//2008 11th IEEE Workshop on Design and Diagnostics of Electronic Circuits and Systems. 2008: 1-6.

[7] Hu Die, Zeng Chun-nian, Liang Hong. Autocalibration method of MEMS accelerometer[C]//2011 International Conference on Mechatronic Science, Electric Engineering and Computer(MEC). 2011: 1348-1351.

[8] Touboul P. Space accelerometers: present status[M]. Springer, 2001: 273-291.

[9] Fan Da, Liu Ming-jie, Liu Yun-feng, et al. Servo loop design of capacitive MEMS accelerometer under high preload voltage[C]//Proceedings of the 2011 Chinese Control and Decision Conference(CCDC). 2011: 1341-1344.

[10] 刘爽, 刘云峰, 董景新. 静电悬浮加速度计反馈引起闭环零点漂移机理及抑制方法[J]. 中国惯性技术学报, 2014, 22(5): 682-687. Liu Shuang, Liu Yun-feng, Dong Jing-xin. Mechanism and suppression method for feedback-caused close-loop position fluctuation of electrostatically suspended accelerometer[J]. Journal of Chinese Inertial Technology, 2014, 22(5): 682-687.

Closed-loop equilibrium position adjustment of electrostatic accelerometer based on equivalent varying preload

LIU Shuang, LIU Yun-feng, HAN Feng-tian, XU Zhe, DONG Jing-xin
(Key Laboratory for High-precision Inertial Instrument and System Technology of the Ministry of Education, Department of Precision Instrument, Tsinghua University, Beijing 100084, China)

The closed-loop equilibrium position(CLEP) has an important impact on the performance of electrostatic accelerometer(EA), which is based on differential-capacitance position sensing. The deviation of CLEP from mechanical zero point would result in scale-factor nonlinearity. In order to adjust the CLEP accurately, a novel method based on equivalent varying preload is proposed to accurately adjust the CLEP in the presence of asymmetry in preload and feedback voltages. An experiment is carried out with the prototype EA to verify the above method. The results show that the quadratic term coefficient, which stands for the nonlinearity of the scale factor, decreases to -3.3×10-8from -1.7×10-7after adjusting CLEP, verifying the effectiveness of the above method.

nonlinearity; varying preload; closed-loop equilibrium position; electrostatic accelerometer

U666.1

A

1005-6734(2015)04-0550-05

10.13695/j.cnki.12-1222/o3.2015.04.024

2015-04-24；

2015-07-27

国家自然科学基金（91436107）

刘爽（1985—），男，博士研究生，从事微重力测量关键技术研究。E-mail：s-liu08@mails.tsinghua.edu.cn

联 系 人：董景新（1948—），男，教授，博士生导师。E-mail：dongjx@mail.tsinghua.edu.cn