基于SINS/LBL紧组合的AUV水下导航定位技术

张 涛，石宏飞，徐晓苏

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

基于SINS/LBL紧组合的AUV水下导航定位技术

张 涛1,2，石宏飞1,2，徐晓苏1,2

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

针对因水下环境的特殊性AUV难以实现精准导航的问题，设计了一种基于SINS/LBL紧组合的AUV水下导航定位系统。该系统具有定位精度高、鲁棒性好等优点，系统由SINS、LBL、DVL和MCP组成，根据LBL的TDOA定位原理建立了LBL斜距差模型，给出了SINS/LBL/DVL/MCP的状态方程和量测方程，利用集中kalman滤波器对组合导航系统进行最优估计。在相同的仿真条件下，对SINS/LBL松组合、紧组合进行了软件仿真，仿真结果表明：相对于松组合系统，基于SINS/LBL的紧组合系统导航精度更高，尤其是在由于AUV运动或受到外界干扰导致可用信号的水听器不足四个时，紧组合系统的可靠性和容错性更高。

AUV；捷联惯导；长基线；紧组合；松组合

AUV（Autonomous Underwater Vehicle，自主式水下航行器）是一种自主式、智能化、能完成水下探测、运载、打捞等多种功能的水下工具，由于水下环境的特殊性，实现AUV的精准导航仍很困难，导航问题是AUV所面临的主要技术挑战之一[1]。由于单一的导航系统自身存在不足，因而组合导航技术已成为导航技术发展的重要方向之一，目前国内外应用于AUV的水下自主导航技术主要以SINS(Strapdown Inertial Navigation Systems，捷联式惯性导航系统)和DVL（Doppler Velocity Log，多普勒计程仪）的组合导航主，辅以GPS(Global Positioning System，全球定位系统)、水声定位系统、MCP(Magnetic compass，磁罗经）等修正，能有效提高系统的导航精度[2-6]。

LBL（Long Base Line，长基线）水声定位系统利用AUV上的声源与海底水听器阵之间的距离信息来求解AUV位置，因其作用范围广、定位精度高已广泛应用于水下潜器[7]。根据参与组合物理量的不同，SINS与LBL的组合方式可分为松组合和紧组合。基于SINS与LBL松组合的系统是根据LBL计算得到的位置来辅助修正SINS导航系统，它需要四个以上的水听器来确定AUV的位置信息[8]。当由于AUV运动或外界干扰使可用水听器数量少于四个时，LBL将无法进行定位，从而无法进行松组合，将导致AUV无法完成准确定位。因此，有必要对AUV水下组合导航技术进行进一步的研究。

针对上述SINS/LBL松组合的缺陷，本文提出了一种基于SINS/LBL紧组合的AUV水下导航定位系统，该系统由SINS、LBL、DVL、MCP组成。在LBL水声定位原理的基础上建立了LBL斜距差模型，并详细推导了SINS/LBL紧组合的状态方程和量测方程，利用卡尔曼滤波技术对组合系统进行最优估计。在相同条件下对松、紧组合系统进行了仿真，仿真结果表明，紧组合系统的导航精度更高，误差曲线平滑，且当可用水听器不足四个时，紧组合系统具有更好的导航性能。

1 基于SINS/LBL紧组合水下组合导航系统原理

针对水下实际使用环境，仅SINS/LBL紧组合系统难以提供全面的导航信息，考虑到DVL(Doppler Velocity Log，多普勒计程仪)能够完全自主导航，隐蔽性好，在浅海和低速时测得AUV相对海底的航行速度精度高，MCP（Magnetic Compass Pilot）成本低，可靠性高，可提供航向信息，因此可选取SINS、LBL、DVL和MCP四个子系统来组成AUV组合导航系统。

图1 SINS/LBL紧组合水下组合导航系统结构示意图Fig.1 Structure of underwater integrated navigation system based on SINS/LBL tightly coupled system

图1所示为基于SINS/LBL紧组合水下组合导航系统结构示意图，组合系统由SINS、LBL、DVL和MCP四个子系统组成。其中，SINS作为主导航系统，根据SINS解算的AUV位置和多个水听器位置得到基于SINS的斜距差，利用TOA(Time of Arrival，到达时间)或TDOA(Time Difference of Arrival，到达时间差)方法得到基于LBL的斜距差，以上两个斜距差之差作为观测量之一输入至Kalman滤波器。另外，DVL提供速度信息，MCP提供航向信息，分别与SINS解算得到的速度和航向值之差也作为观测量，经Kalman信息融合后得到各导航参数误差反馈校正SINS从而提高导航精度。

1.1 基于 LBL的斜距差模型的建立

LBL水声定位系统是由安装在AUV的声源和布放在海底的水听器阵构成的定位系统，海底水听器之间的距离一般为100～6000 m，通过测量声源到达水听器的时延解算出声源与水听器之间的距离，再由其几何关系解算出AUV的位置。常用定位算法有TOA和TDOA。与TOA不同，TDOA是通过检测声信号到达两个水听器的时间差，而不是到达的绝对时间来确定AUV的位置，对海底水听器的时间同步不作要求，因此，本文采用基于TDOA方法辅助SINS进行定位。

图2 LBL水声定位示意图Fig.2 Schematic LBL acoustic positioning

图2为LBL水声定位示意图。LBL水声定位系统由安装在AUV上的声源和布放在海底的四个水听器组成。以地球直角坐标系为全局坐标系，假设AUV位置坐标为(x,y,z)，四个水听器的位置坐标为(xi,yi,zi)，则AUV与水听器之间的斜距可表示为

在TDOA方法下，通过对各水听器接收声源信号做广义互相关得到声源信号传播至各水听器的时间差，再乘以声速则得到对应的斜距差Ri-R0。

由于时延差测量、声传播的多途径效应等将引起斜距差测量有误差，为简化模型，可将斜距差误差用一阶马尔科夫过程表示，则斜距差[9-10]可表示为

1.2 SINS/LBL紧组合状态方程和量测方程

紧组合系统状态方程描述为

式中，XSINS、XLBL分别为SINS、LBL的状态变量，FSINS、FLBL分别为SINS、LBL系统矩阵，WSINS、WLBL分别为SINS与LBL的系统噪声。

SINS选择速度误差、姿态误差、位置误差、加速度计零偏和陀螺漂移作为状态量：

式中，δVE、δVN、δVU分别是捷联东向、北向、天向的速度误差，φE、φN、φU分别是捷联东向、北向、天向的失准角，δL、δλ、δh分别是捷联纬度、经度、高度误差，∇bx、∇by、∇bz为捷联加表三个轴向的偏置误差，εbx、εby、εbz是捷联陀螺的三个轴向漂移。FSINS可由SINS误差方程确定。

式中，δRi(i=1,2,3)斜距差误差。

量测方程描述为

式中，ρSINSi-ρLBLi为SINS解算的各水听器与声源的斜距差与LBL测量得到的斜距差的差值，ηLBL为量测噪声。

设SINS解算的AUV位置为（xS,yS,zS），则有

相对AUV真实位置（x,y,z）将上式线性化得

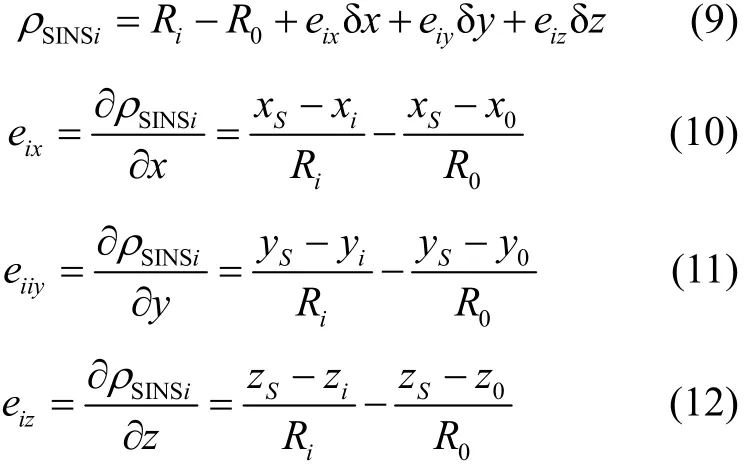
式中：

LBL斜距差为

于是：

当系统采用地球直角系（Oxeyeze）作为导航坐标系时，可用式(15)构造系统量测方程。实际应用中是以经纬度和高度定位的，因此要把dx、dy、dz用dl、dλ、dh 表示。

其非零元素如下：

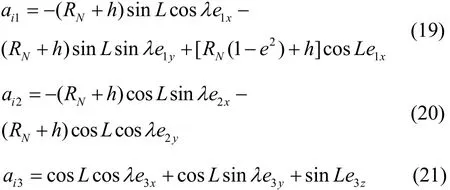
式中，i=1,2,3，RN为参考椭球体子午面内的曲率半径，RE为垂直子午面的法线平面内的曲率半径，e为椭球的椭圆度。

2 组合系统模型的建立

组合系统包括SINS、LBL、DVL和MCP四个子系统，Kalman滤波器的状态量依次选取SINS选择速度误差、姿态误差、位置误差、加速度计零偏和陀螺漂移，LBL斜距差的随机误差，DVL的速度误差，MCP的航向角误差，共22个变量。SINS/LBL紧组合状态方程和量测方程如上节所述。

2.1 SINS/DVL状态方程和量测方程

选取多普勒测速仪的测速误差作为状态变量：

式中：δVDi(i=x,y,z)为地形变化引起的测速误差，可用一阶马尔科夫过程近似描述。

式中，Cij(i=1,2,3;j =1,2,3)为姿态转移矩阵的元素，ηDVL为DVL量测噪声。

2.2 SINS/MCP状态方程和量测方程

选取磁罗经输出的航向角误差作为状态变量：

δψMCP可设为随机常值，于是：

式中，ηMCP为MCP量测噪声。

3 系统仿真及分析

为验证基于SINS/LBL紧组合的水下组合导航系统的性能，在C++ 环境下进行了1 h的仿真，仿真条件如下：AUV运动模型为三轴正弦摇摆运动，纵摇幅度分别为9°，摇摆周期为8 s，横摇幅度分别为12°，摇摆周期为10 s，航向幅度分别为14°，摇摆周期为6 s，初始相位均为零。SINS惯性器件的性能参数如下：陀螺仪随机漂移均为0.06 (°)/h，常值漂移均为0.06 (°)/h，加速度计随机漂移均为50 μg，常值偏置均为100 μg；初始失准角：纵摇角1.5°，横摇角1.5°，航向角1.5°；LBL斜距差随机漂移为5 m，常值偏置为5 m，DVL速度误差为0.2 m/s，MCP精度优于3°。

图3所示为AUV理想运动轨迹与海底水听器阵位置图。AUV在深度为100 m的水下以初始航向角45°做匀速直线运动，航速为4 m/s，姿态更新周期为10 ms；AUV的初始位置为：纬度L=32°，经度λ=118°；海底布放两个水听器阵列，水听器接收信号距离均为2.5 km，为简化分析，假设所有的水听器都在同一平面内，水听器阵列1（图3左下方蓝色圆圈所示）的四个水听器的位置分别为(117.995°, 32°)、(118°, 31.995°)、(118.005°, 32°)、(118°, 32.005°)，水听器阵列2（图3右上方蓝色圆圈所示）的四个水听器的位置分别为(118.100°, 32.090°)、(118.105°, 32.085°)、(118.110°, 32.090°)、(118.105°, 32.095°)。仿真结果如图4～图7所示。

图3 AUV理想运动轨迹与海底水听器阵位置图Fig.3 Ideal trajectory of AUV and the seabed hydrophone array locations.

图4 SINS/LBL紧组合姿态误差曲线Fig.4 Curves of attitude error of SINS/LBL tightly coupled system

图5 SINS/LBL紧组合速度误差曲线Fig.5 Curves of velocity error of SINS/LBL tightly coupled system

图4～图6为SINS/LBL紧组合姿态、速度和位置误差曲线，由图可知：在0～625 s内AUV行驶在水听器阵列1接收信号范围内，LBL提供三个斜距差观测量与SINS作紧组合，位置误差小于5 m，其他误差小且稳定；在625～800 s时，AUV逐渐驶离长基线阵列1的距离范围，此时仍有两个水听器可以接收到声源信号，提供一个斜距差观测量与SINS进行紧组合，此时导航误差仍较小；在800～2800 s内AUV进入LBL信号盲区，由于失去位置信息校正，各导航误差增大，并且位置误差有发散的趋势；在2800～2975 s内，AUV逐步靠近水听器阵列2信号区，有两个水听器可以提前接收到声源信号，使得导航误差逐渐减少；在2800～3600 s内，AUV完全驶入水听器阵列2，四个水听器均能接收到声源信号，导航误差保持较小且稳定，且位置误差恢复至5 m以内。

图6 SINS/LBL紧组合位置误差曲线Fig.6 Curves of position error of SINS/LBL tightly coupled system

图7 SINS/LBL松组合位置误差曲线Fig.7 Curves of position error of SINS/LBL loosely coupled system

图7为松组合误差曲线，只有接四个以上的水听器接收到声源信号时，松组合算法才可以正常执行，位置误差为10 m，一旦接收到信号的水听器数量小于四个时无法定位，因此松组合失效，位置误差发散。

上述分析表明，相对于松组合系统，SINS/LBL紧组合系统导航精度更高，尤其在由于AUV运动或受到外界干扰导致可用信号的水听器不足四个时，紧组合系统的可靠性和容错性更高。

4 结 论

本文针对SINS与LBL松组合的缺陷，设计了一种基于SINS/LBL紧组合的AUV水下导航定位系统。整个组合系统由SINS、DVL、LBL和MCP四个子系统组成，在建立LBL斜距差模型的基础上详细推导了SINS/LBL紧组合的状态方程和量测方程，利用集中Kalman滤波技术进行最优估计补偿组合系统。

通过系统仿真结果可以看出，相对于松组合系统，基于SINS/LBL紧组合的AUV水下导航定位系统能有效提高导航精度，具有较好的抗干扰性。

（References）：

[1] 王小峰. 水下航行器INS/GPS/DVL组合导航方法[J]. 鱼雷技术, 2010, 18(4): 287-290. Wang Xiao-feng. New application of federated filter in INS/GPS/DVL integrated navigation system for AUV[J]. Torpedo Technology, 2010, 18(4): 287-290.

[2] 张涛, 徐晓苏, 李瑶, 等. 基于惯导及水下声学辅助系统的AUV容错导航技术[J]. 中国惯性技术学报. 2013, 21(4): 512-516. Zhang Tao, Xu Xiao-su, Li Yao, et al. AUV fault-tolerant technology based on inertial navigation and underwater acoustics assisted navigation system[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 512-516.

[3] Morgado M, Paulo O, Carlos S, et al. Embedded vehicle dynamics aiding for USBL/INS underwater navigation system[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 322-330.

[4] Miller P A, Farrell J A, Zhao Yuan-yuan, et al. Autonomous underwater vehicle navigation[J]. IEEE Journal of Oceanic Engineering, 2010, 35(3): 663-678.

[5] Marco D B, Healey A J. Command, control, and navigation experimental results with the NPS ARIES AUV[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 466-476.

[6] Liu Yu, Li X R. Aided strapdown inertial navigation for autonomous underwater vehicles[C]//Proc. SPIE of Signal and Data Processing of Small Targets. 2010: 2654-2662.

[7] 田坦. 水下定位与导航技术[M]. 北京: 国防工业出版社, 2007.

[8] 范欣, 张福斌, 张永清, 等. 多传感器信息融合的水下航行器组合导航方法[J]. 火力与指挥控制, 2011, 36(3): 78-81. Fan Xin, Zhang Fu-bing, Zhang Yong-qing, et al. Information fusion technology and its application to multi-sensor integrated navigation system for autonomous underwater vehicle[J]. Fire Control & Command Control, 2011, 36(3): 78-81.

[9] Pan-Mook Lee, Jun Bong-Huan, Kim Kihun, et al. Simulation of an inertial acoustic navigation system with range aiding for an autonomous underwater vehicle[J]. IEEE Journal of Oceanic Engineering, 2007, 32(2): 327-345.

[10] Pan-Mook Lee, Jun Bong-Huan, Choi Hyun Taek, et al. An integrated navigation systems for underwater vehicles based on inertial sensors and pseudo LBL acoustic transponders[C]//Proceedings of OCEANS 2005 MTS/IEEE. 2005: 555-562.

Positioning technology based on SINS / LBL tightly coupling for AUV underwater navigation system

ZHANG Tao1,2, SHI Hong-fei1,2, XU Xiao-su1,2
( 1. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 2. Key Lab of Micro Inertial Instruments and Advanced Navigation Technology of Education Ministry, Southeast University, Nanjing 210096, China)

AUVs(Autonomous Underwater Vehicle) are hardly to achieve precise navigation due to the particularity of the underwater environment. In this paper, an underwater navigation of AUV based on SINS/LBL tightly coupled system was designed. The system is composed of SINS, LBL, DVL and MCP, and has such advantages as high precision and good robustness, etc.. The LBL slant-range difference model was established according to the TDOA location principle of LBL. The SINS/LBL/DVL/MCP state equation and measurement equation were given. The centralized Kalman filter was applied to the optimal estimation of the integrated navigation system. The software simulations of SINS/LBL loosely coupled and tightly coupled systems were conducted in the same simulation conditions. The results show that, compared with the loosely coupled system, the navigation precision of the SINS/LBL tightly coupled system is higher, and the reliability of the SINS/LBL tightly coupled system is better especially when the number of available hydrophones is less than four caused by AUV movement or outside disturbance.

autonomous underwater vehicle; SINS; long base line; tightly coupled; loosely coupled

V249.3

A

1005-6734(2015)04-0500-05

10.13695/j.cnki.12-1222/o3.2015.04.015

2015-03-09；

2015-06-30

国家自然科学基金资助项目（51375088）；微惯性仪表与先进导航技术教育部重点实验室基金（201403）；优秀青年教师教学科研资助计划（2242015R30031）

张涛（1980—），男，博士，副研究员，从事组合导航研究。E-mail：ztandyy@163.com