天文观测角辅助的高超声速飞行器传递对准方法

戴晨曦，程向红，陈红梅，刘峰丽

（1. 东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 航天恒星科技有限公司 天地一体化信息技术国家重点实验室(筹)，北京 100086）

天文观测角辅助的高超声速飞行器传递对准方法

戴晨曦1，程向红1，陈红梅1，刘峰丽2

（1. 东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 航天恒星科技有限公司 天地一体化信息技术国家重点实验室(筹)，北京 100086）

针对复杂环境下高超声速飞行器的可靠、精确和快速的传递对准需求，提出了一种基于星敏感器天文观测角(高度角、方位角)的传递对准算法。以发射点惯性坐标系为导航系，分析了惯导系统在惯性系下的误差方程，提出了大失准角情况下的基于星敏感器天文高度角、方位角匹配的对准算法。针对该系统状态方程和量测方程的非线性特性，采用UKF滤波算法进行了仿真。仿真结果表明：观测星数达到两颗时，该方案可以在2 s内使得姿态角的估计误差达到13″。仿真验证了该算法的有效性，对其他高空飞行器的传递对准有一定参考价值。

高超声速飞行器；星敏感器；天文观测角；传递对准

高超声速飞行器具有全球到达、突防概率高、天地往返等特点，是当今世界军事竞争的制高点。高超声速飞行器携带的导弹在发射前，其惯导系统需要进行初始对准。弹载捷联惯导的初始对准通常通过传递对准实现，即利用已对准好的高精度的主惯导信息进行对准。由于飞行器本身动态范围大，当初始导航信息不准确时，会造成很大的积累偏差，这对高超声速飞行器传递对准的精度和速度提出了更高的要求。可靠、精确和快速的传递对准是高超声速飞行器的关键技术之一[1]。

高超声速飞行器的传递对准属于空中对准的一种，空中对准的经典方法是James E. Kain和James R.Cloutier提出的“速度+姿态”匹配算法，该方法借助飞机的摇翼在30 s 内可以达到 1 mrad 的精度[2]。考虑到高超声速飞行器所处环境比较复杂，为充分保障对准任务在主惯导精度不高或出现故障的情况下能够可靠完成，需要研究外观测信息辅助的传递对准。文献[3]利用GPS辅助弹载捷联惯导的传递对准，在10 s内水平姿态误差收敛至6′，加速机动下航向姿态误差收敛至17′，姿态精度有限。为提高传递对准的姿态精度，可由天文导航通过星敏感器观测星光来获得姿态信息。

星敏感器能提供高精度的姿态信息[4]，其输出信息的类型包括天文观测角，即星光矢量在星敏感器坐标系中的角度(高度角、方位角，见图1)和飞行器相对于惯性空间的姿态，后者是利用多颗星的观测矢量信息和导航星库预存的导航星在惯性系中的矢量信息，通过姿态确定算法获得，如经典的确定性算法TRIAD[5]。在姿态确定的过程中不免引入误差，所以观测矢量信息相对姿态信息更加准确。国内外学者对星敏感器与捷联惯导的组合方式进行了大量研究[6-9]，文献[7]利用弹载星敏感器辅助天基导弹的传递对准，采用星敏感器输出的姿态进行匹配，在10 s的时间内，对准精度达到1′。文献[8]利用星敏感器输出的高度角、方位角和GPS辅助SINS进行高超声速飞行器的组合导航，与单独的SINS/GPS组合相比，姿态精度有显著提高，且当初始姿态误差较小时，观测一颗星情况下也能在较长时间内对姿态误差起抑制作用。文献[9]针对月球车时停时走的特点，提出了INS/CNS双组合模型，根据月球车的运动状态选择不同的组合模式，提高组合导航的精度。以上文献都采用当地地理坐标系为导航系，而临近空间平台下的飞行器一般以惯性坐标系作为导航坐标系[10]，采用当地水平坐标系将带来多余的坐标转换，给实际应用带来不便。

本文针对高超声速飞行器机动快、结构模型不确定的特点，以发射点惯性坐标系为导航系，提出了以一种基于星敏感器的高超声速飞行器快速传递对准方法，综合考虑万有引力及地球非球形引力摄动等影响，建立了适用于大失准角的状态方程，并以星敏感器的高度角、方位角为观测量建立了的量测方程。针对星敏感器输出的两类姿态信息(高度角、方位角和姿态)，考虑通过观测矢量确定姿态过程中可能造成的误差，比较了利用星敏感器输出的高度角、方位角和姿态进行传递对准的精度和速度。为高超声速飞行器以及其他高空飞行器的传递对准提供了参考。

1 基于星敏感器的传递对准方案设计

高超声速飞行器的传递对准发生在巡航阶段，导弹从飞行器上发射。飞行器上的星敏感器提供姿态信息，辅助弹载子惯导进行传递对准。由于弹载子惯导通常精度不高，姿态存在较大误差，因此需要建立适用于大失准角的传递对准模型。巡航阶段，飞行器高度在30～50 km，处于临近空间，飞行速度在5～8 Ma[1]。临近空间空气较为稀薄，大气散射的太阳辐射较小，星敏感器的可探测星等增大，能够获得较好的性能。

如图1所示，星敏感器固连在飞行器机体上，其观测矢量相对飞行器坐标系的高度角H和方位角A[11]。另一方面，由弹载子惯导提供的弹体姿态、速度、位置，查询导航星在星历中的格林时角和赤纬，可解算弹体坐标系下的星光高度角、方位角。然后以星敏感器输出的高度角、方位角和弹载子惯导解算的导航星高度角、方位角之差为观测量，考虑飞行器挠曲变形角，通过最优估计的方法估计并补偿弹载子惯导的失准角。其具体过程如图2。

图1 星敏感器坐标系下星光高度角、方位角示意图Fig.1 Altitude and azimuth angles of star vector under vehicle coordinate system

图2 基于星敏感器的传递对准原理图Fig.2 Principle of transfer alignment based on star sensors

2 基于星敏感器的传递对准模型

定义坐标系：i为发射点惯性坐标系，p为计算导航坐标系，bs为弹载子惯导坐标系(x、y、z轴分别指向弹体的前、上、右)，bm为飞行器坐标系(也是星敏感器坐标系)，c为地心惯性坐标系，e为地球坐标系，t为当地地理坐标系。高超声速飞行器进行传递对准，首先要建立SINS的系统误差模型和量测模型。

2.1 状态方程

以发射点惯性坐标系为导航系，建立适用于大失准角的传递对准状态方程。状态变量为21维，分别为失准角(φx, φy, φz)、速度误差(δVx, δVy, δVz)、位置误差(δsx, δsy, δsz)、陀螺漂移(εx, εy, εz)、加速度计偏置 (∇x,∇y, ∇z)、星敏感器、飞行器挠曲变形角(ξx,, ξy, ξz)。状态向量X为

对应的状态方程分别为：

① 数学平台失准角方程为

② 发射点惯性坐标系下的速度误差方程为

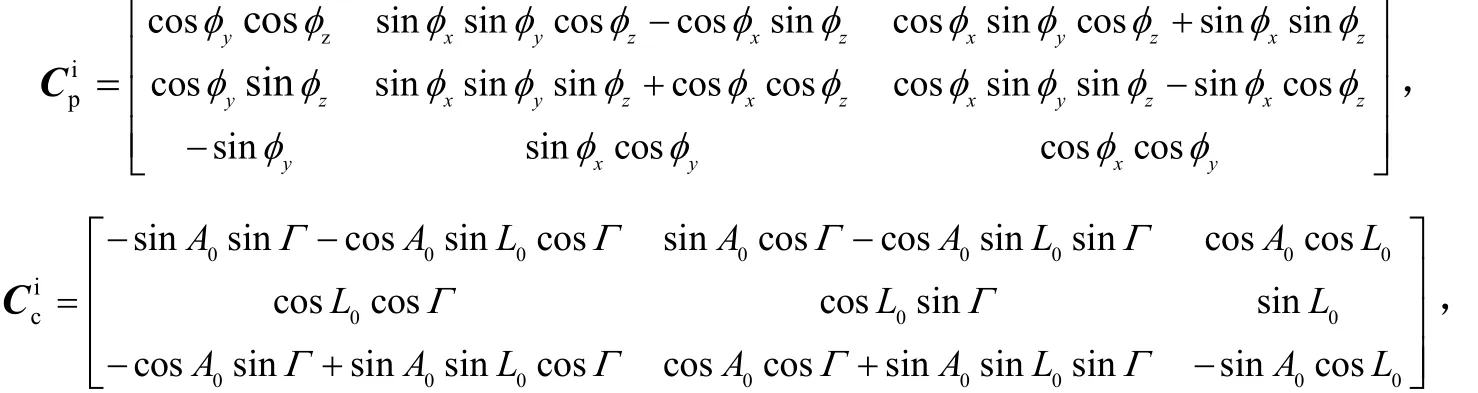
式中，a是万有引力常数，J2是二阶带谐系数，Re是地球半径，r是飞行器的在地心惯性坐标系中的位置矢量。对式(4)进行扰动可以得到：

③ 发射点惯性坐标系下的位置误差模型：

④ 挠曲变形角模型

飞行器的挠曲变形主要受阵风扰动、发动机噪声以及温度场变化等因素的影响，可以视为由随机力函数激发的随机变量，即白噪声激励的马尔科夫过程。设挠曲变形引起的挠性失准角为ξ，则二阶马尔科夫过程如下：

式中：ξ=[ξx, ξy, ξz]T的标准差为σ=[σx, σy, σz]T；η=[ηx, ηy, ηz]T为白噪声，方差为Qη=[Qηx, Qηy, Qηz]T，即η～N(0, Qη)；β=[βx, βy, βz]T为常数。

Qη、σ和β之间有如下关系：

相关时间τi与相应的β有如下关系：

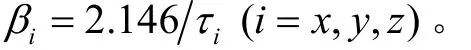
2.2 基于星敏感器传递对准的量测方程

将弹载子惯导解算得到的高度角Hcbs、方位角Acbs与星敏感器获得的高度角Hobm、方位角Aobm相减，得到高度角误差ΔHb和方位角误差ΔAb作为观测量，量测方程为

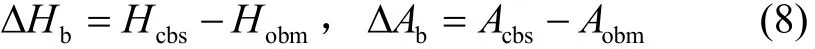
当地地理坐标系下解算的高度角Hct、方位角Act为

式中：tEc为子午线角，

Dec为导航星的赤纬，GHA为格林时角，Latitcbs和Longicbs为弹载子惯导系统解算得弹体的纬度和经度。

由高度角Hct、方位角Act可得到当地地理坐标系下的解算观测矢量rct=[rctx, rctyr,ctz]T，再利用弹载子惯导的导航参数计算得到姿态矩阵，即可得到弹体坐标系的观测矢量rcb=[rcbx, rcby, rcbz]。其中，当地地理坐标系下的解算观测矢量为

姿态转换矩阵为

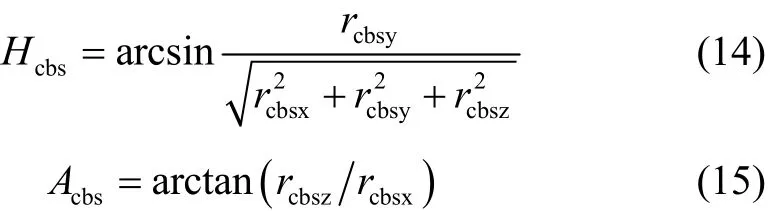
弹载子惯导坐标系下的星光高度角、方位角误差是由弹载子惯导解算的位置误差、姿态误差、弹载子惯导挠曲变形误差造成。星敏感器观测的高度角、方位角可通过补偿上述误差获得。

发射点惯性系的位置误差为si=ˆi-δsi，其中，

地心惯性坐标系的位置sc=si，地球坐标系的位置se=sc。当地地理经纬度：

导航星距离地球很远(最近距离为4光年)，星光到达地球的观测矢量可视为平行，所以星敏感器观测的观测矢量表示为

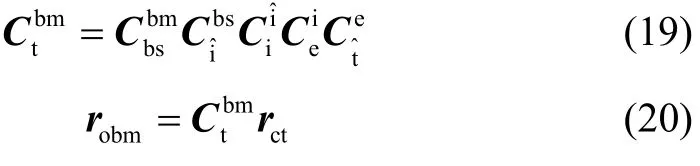
最后由式(20)得到星敏感器观测的高度角、方位角：

3 仿真与分析

设飞行器位于东经116.346°，北纬39.984°，处于巡航阶段[12]，对准初始时刻飞行器速度为3 Ma，高度为50 km。弹载子惯导初始航向角误差为20°，初始俯仰角误差为10°，初始横滚角误差为10°；陀螺仪x、y和z方向常值漂移均为0.05 (°)/h，随机噪声为0.001 (°)/√h，加速度计在x、y和z方向常值偏置均为0.1mg，随机噪声为0.05 mg。高超声速飞行器的变形频率较高，接近10 Hz，设其挠曲二阶马尔科夫过程x、y和z方向的时间常数分别为0.3 s、0.4 s、0.5 s[13]，三个挠曲变形角的标准差均为3'。SINS输出数据频率为1000 Hz，滤波周期为0.1 s，仿真时间为20 s。考虑到利用星敏感器的观测矢量确定姿态可能造成的误差，设星敏感器输出的高度角、方位角精度为3″，姿态角精度为4″。仿真结果见图3和表1。

表1 两颗星传递对准姿态估计误差Tab.1 Attitude estimation errors of transfer alignment using information apparently from two and three stars

图3 不同导航星数传递对准姿态误差Fig.3 Attitude estimation errors of transfer alignment under different star conditions

由图3和表1，比较利用星敏感器的姿态信息和不同导航星数情况下的传递对准效果。就精度而言，利用三星信息的传递对准精度稍高，能收敛至8″左右，姿态匹配的误差最大为9″，两颗星的精度稍低，能收敛到13″左右，观测到一颗导航星时，姿态误差不收敛。就收敛速度而言，三种匹配方式均能在2 s内收敛，其中利用三星信息进行传递对准基本能在1 s内收敛。上述结果表明，基于星敏感器高度角、方位角匹配的传递对准在观测到两颗以上导航星时，能够实现对弹载子惯导姿态误差的快速、精确估计。

4 结 论

针对高超声速飞行器的特点，提出发射点惯性坐标系下基于星敏感器高度角、方位角匹配的传递对准方法，利用星敏感器的高精度姿态信息修正弹载子惯导的姿态误差。仿真结果表明，当星敏感器观测的导航星数目为一颗时，无法进行传递对准，当导航星数达到两颗时，弹载子惯导的姿态误差能够在2 s内收敛至13″，导航星数目的增加一定程度上会提高传递对准的效果。在假设星敏感器输出的姿态精度比高度角、方位角精度低1″的前提下，利用三星信息比利用星敏感器姿态信息的传递对准精度稍高。考虑到临近空间空气稀薄，没有遮挡，只观测到一颗导航星的情况极少，大视场星敏感器观测到多颗星的概率很高[8]，极大提高了直接利用多星观测矢量信息进行传递对准的可行性。该方案同样适用于其他高空飞行器的传递对准，具有较好的参考价值。

（References）：

[1] 黄伟, 罗世彬, 王振国, 等. 临近空间高超声速飞行器关键技术及展望[J]. 宇航学报, 2010, 31(5): 1259-1265. Huang Wei, Luo Shi-bin, Wang Zhen-guo, et al. Key techniques and prospect of near-space hypersonic vehicle [J]. Journal of Astronautics, 2010, 31(5): 1259-1265.

[2] Kain J E, Cloutier J R. Rapid transfer alignment for tactical weapon applications[C]//AIAA Guidance, Navigation and Control Conference. 1989: 1290-1300.

[3] 吴枫, 秦永元, 成研, 等. 基于GPS的弹载捷联惯导动基座传递对准技术[J]. 中国惯性技术学报, 2013, 21(1): 56-60. Wu Feng, Qin Yong-yuan, Chen Yan, et al. Transfer alignment for missile-borne SINS using airborne GPS on moving base[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 56-60.

[4] Mao Xin-yuan, Du Xiao-jing, Fang Hui. Precise attitude determination strategy for spacecraft based on information fusion of attitude sensors[J]. International Journal of Aeronautical and Space Sciences, 2013, 14(1): 91-98.

[5] Habib T M A. A comparative study of spacecraft attitude determination and estimation algorithms (a cost–benefit approach) [J]. Aerospace Science and Technology, 2013, 26(1): 211-5.

[6] Wu Xiao-juan, Wang Xin-long. A SINS/CNS deep integrated navigation method based on mathematical horizon reference[J]. Aircraft Engineering and Aerospace Technology, 2011, 83(1): 26-34.

[7] 马闪, 王新龙. 天基导弹的动基座快速精确传递对准方法[J]. 红外与激光工程, 2007, 36(z2): 503-507. Ma Shan, Wang Xinlong. Rapid precise transfer alignment of space missile on moving base[J]. Infrared and Laser Engineering, 2007, 36(z2): 503-507.

[8] 王融, 熊智, 刘建业, 等. 天文角度辅助的高超声速飞行器多信息融合导航算法[J]. 中国惯性技术学报, 2013, 21(4): 484-488. Wang Rong, Xiong Zhi, Liu Jian-ye, et al. Multi-information fusion navigation algorithm assisted by celestial angle observation for hypersonic cruise vehicle[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 484-488.

[9] Ning Xiao-lin, Liu Ling-ling. A two-mode INS/CNS navigation method for lunar rovers[J]. Instrumentation and Measurement, 2014, 63(9): 2170-2179.

[10] Chen K, Zhao G, Meng Z, et al. Transfer alignment for experiment’s INS on space moving platform[C]//4th IEEE Conference on Industrial Electronics and Applications. 2009: 1823-1827.

[11] Wu Xiaojuan, Wang Xin-long. A SINS/CNS deep integrated navigation method based on mathematical horizon reference[J]. Aircraft Engineering and Aerospace Technology, 2011, 83(1): 26-34.

[12] Bahm C, Baumann E, Martin J, et al. The X-43A Hyper-X Mach 7 flight 2 guidance, navigation, and control overview and flight test results[J]. AIAA paper, 2005, 3275: 2005.

[13] Grasso F, Purpura C, Chanetz B, et al. Type III and type IV shock/shock interferences: theoretical and experimental aspects[J]. Aerospace Science and Technology, 2003, 7(2): 93-106.

Transfer alignment approach of hypersonic vehicle aided by celestial angle

DAI Chen-xi1, CHENG Xiang-hong1, CHEN Hong-mei1, LIU Feng-li2
(1. School of Instrument Science and Engineering, Key Laboratory of Micro Inertial instrument and Advanced Navigation technology, Ministry of Education, Southeast University, Nanjing 210096, China; 2. Space Star Technology Co., Ltd. State Key Laboratory of Space-Ground Integrated Information Technology, Beijing 100086, China)

A transfer alignment method based on star sensor’s celestial angle (altitude angle and azimuth angle) is proposed to serve the need of rapidly responsive, reliable and precise transfer alignment method of hypersonic vehicle under complex environment. The error equation of navigation system under inertial coordinate system is analyzed. A transfer alignment algorithm suitable for large azimuth misalignment is established under the launch-point inertial coordinate system using matching model based on altitude angle and azimuth angle. An UKF algorithm is applied to implement the simulation on account of the nonlinear feature of the state and measurement equations. The simulation results show that the transfer alignment cannot be accomplished by using the information of one star, while the three attitude angles can converge to 13″ within 2 s by using the information from two or more stars. The simulation verifies the effectiveness and applicability of the proposed method, which could also provide references for the transfer alignment of other high altitude vehicles.

hypersonic vehicle; star sensors; celestial observation angles; transfer alignment

U666.1

A

1005-6734(2015)04-0446-05

10.13695/j.cnki.12-1222/o3.2015.04.006

2015-03-18；

2015-06-30

天地一体化信息技术国家重点实验室(筹)开放基金资助（2014_CXJJ-DH_08）

戴晨曦（1990—），女，博士研究生，从事导航算法研究。E-mail：DaiChenxi_seu@163.com

联 系 人：程向红（1963—），女，教授，博士生导师。从事惯性技术及其应用研究。E-mail：xhcheng@seu.edu.cn