基于近景摄影的栅格空间量测法
徐万里, 鲍 硕, 刘玉军
(装甲兵工程学院信息工程系,北京 100072)
基于近景摄影的栅格空间量测法
徐万里, 鲍 硕, 刘玉军
(装甲兵工程学院信息工程系,北京 100072)
针对近景摄影中传统的测量算法误差较大、计算过程较繁琐的问题,提出了一种新的测量算法——栅格空间量测法。该算法直接由标定点的像点构造一个理想的栅格量测空间,将感兴趣的物点通过其像点映射到该栅格量测空间,经与栅格网点的数据按距离进行融合后得出其定位值。最后通过实验对该算法进行了验证,结果表明:该算法的测量误差控制在忽米级,定位精度明显优于传统算法且计算简便。
近景摄影;栅格量测空间;栅格空间量测法;误差控制
摄影测量是从几何角度由像点的信息计算出物点的位置[1]。近景摄影测量一般指100 m内的摄影测量[2],如算法得当,则可获得很高的计算精度,其测量的绝对误差可以控制在忽米级[3-4],可用于对高精度工件进行加工控制以及对其他测量仪器进行检验校正,具有较高的实用价值[5]。
目前,为了能够利用像点的坐标确定其所对应空间物点的确切位置,多采用立体摄影测量方法[6-7]。所谓立体摄影测量,就是在2个不同的摄影站上对同一个物体各自进行拍摄,构成立体像对,根据摄影过程的几何反转理论,由2张相片上同名像点的坐标计算出所对应空间物体的三维坐标[8-9]。但在实际测量中,由于受拍摄环境误差的影响,如2台相机主距不同、相机倾斜、标定点本身不准确等各种不可消除误差源的存在,将直接影响测量精度[10]。传统的摄影测量算法(如直接线性变换解法[11-12]等)通常是逐个解算方位元素并进行修正,计算过程相当繁琐,且精度提高不明显。因此,测量算法的研究便成为提高定位精度的核心问题[13]。
对于近景摄影测量,可采用人工标定点作为控制点[2,14],鉴于此有利条件,本文提出了栅格空间量测法,并通过实验进行验证。
1 模型建立
设摄测坐标系S1-XYZ是以左相机焦点S1为坐标原点,以过S1的铅垂线为Z轴,以左主光轴S1、O1为Y轴,两相机焦点S1、S2的连线(即基线)为B,相机的主距为f,实际中相片位于相机焦点后方,为不失一般性,将相片反演到焦点前方,如图1所示。
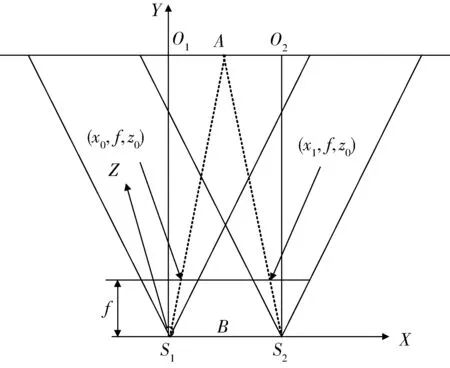
图1 摄测坐标系
假设物点A在摄测坐标系S1-XYZ下的坐标为(XA,YA,ZA),其在左、右相片中所对应同名像点在摄测坐标系S1-XYZ下的坐标分别为(x0,f,z0)、(x1,f,z0),而物点、像点与相机焦点在同一直线上,故由物点和像点坐标得到2条直线方程为
由于2台相机焦点的坐标分别为(0,0,0)、(B,0,0),分别在上述2条直线上,故有
(1)
对于一个平行于相片平面且与焦点距离为Y的物体平面上,任意一条长度为L的线段与相片中对应实际距离l的像素段均有以下关系:
Y/f=L/l。
(2)
由式(1)、(2)可得两相机焦点的基线为
B=p/(1-l/L)。
(3)
为了求出相机的主距f,可按以下步骤进行计算。假设有一平面板与焦点的纵深距离为Yi,将其记为第i平面,将此平面板沿垂直于主光轴方向平行移动到距离焦点Yj的位置,将其记为第j平面,在第i平面的相片中找到任意2个距离为L的标定点,记这2个标定点间隔的像素数为li,在第j平面的照片中找到相应的2个标定点,其间隔的像素数为lj,则这2个标定点在第i、j平面相片中的实际距离分别为li×Δx和lj×Δx,其中Δx为每个像素的实际宽度。
由式(2)可知
Yi/f=L/(li×Δx),
(4)
Yj/f=L/(lj×Δx)。
(5)
将式(5)和式(4)相减,可求得

(6)
由式(6)可知:在实际计算中并不要求测得Yi的实际值,而只要求测得Yj与Yi的差值即可。另外,由式(4)可知:求得f后,可求出第i平面相对于相机的实际纵深距离为
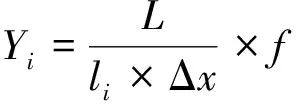
(7)
2 栅格空间量测法
求得主距f和实际纵深距离Yi后,采用栅格空间量测法可计算出物点的实际位置,具体步骤如下。
1) 建立栅格量测平面,如图2所示。用一张420 mm×420 mm的平面玻璃板作辅助,玻璃板上标有刻度,每隔20 mm刻有标定点,呈网格状。将玻璃板所在的平面记为0-平面,在0-平面的相片中取出靠近相机主光轴那一行的标定点,根据第1个标定点和最后一个标定点的像素坐标计算出每2个相邻标定点间隔的像素数l0,以靠近主光轴的第1个标定点为起点,以l0为间隔依次向外扩展,构造一个具有标定点的栅格量测平面,记下玻璃板上标定点的误差。

图2 栅格量测平面
2) 建立栅格量测空间,即直接由标定的像点构造一个理想的栅格量测空间。
由式(4)可知:任一平面上任意一点到主点的水平距离L与这一点的像素坐标xi应有关系式
Yi×xi×Δx=L×f,i=0,1,2,…,N,
即
Yi×xi=C,i=0,1,2,…,N,
式中:C=Lf/Δx,为常数。
对于平面上任意一点,对应其在第i、j平面(i,j=0,1,2,…,N)都有
Yi×xi=Yj×xj,
即

(8)
由式(8)可知:任给某一平面的纵深距离,可以根据0-平面中像素的水平坐标和纵深距离推算出这一平面中像素的水平坐标。同理,可以根据0-平面中像素的垂直坐标推算出其他平面中像素的垂直坐标。故由0-平面的栅格量测平面可以推算出其他纵深距离上的栅格量测平面,从而就得到一个栅格量测空间。
3) 建立栅格量测空间后,将相片与栅格量测空间中的点建立一一对应关系,将感兴趣的物点通过其像点映射到该栅格量测空间,经与栅格网点的数据按距离进行融合后得出其定位值,即该点的坐标值。
记相片中第i行、第j列的标定点为oij,i,j=1,2,…,21,加上误差修正后对应到栅格量测平面中第i行、第j列的标定点为Oij,i,j=1,2,…,21,相片中不在标定点上的像点坐标则按距离融合公式
对应到栅格量测平面中。
其中:(x,z)为相片中位于oi j、oi j+1、oi+1 j、oi+1 j+14个标定点所构成方框内的像点o的坐标;(xi j,zi j)、(xi j+1,zi j+1)、(xi+1 j,zi+1 j)、(xi+1 j+1,zi+1 j+1)分别为上述4个标定点的修正像素坐标;(Xi j,Zi j)为栅格量测平面中第i行、第j列标定点的像素坐标;l为栅格量测平面的扩展像素间隔。则(X,Z)即为物点对应到栅格量测平面中的像素坐标,再由式(1)可求出物点的实际位置。
3 实验验证
本实验是在中国计量科学研究院的实验室中进行的,所使用相机为上海相机制造厂特制,型号为Hasselblad CFV-50,分辨率为8 176×6 132像素,像元为0.005 993 15 mm。
采用如图2所示栅格量测平面测量一个国际通用标准器。标准器标定了3个球心间的距离,若从左至右依次设定为球1、2、3、4,则有球1到球2距离为99.990 9 mm,球3到球4距离为150.003 4 mm,球1到球4距离为300.003 8 mm。测量时,将标准器分别摆放成10组不同的角度进行拍照,由式(6)可以计算出相机的主距为79.301 9 mm。
在图像处理中,为了减小计算量,首先由TIFF格式的RGB图转换为BMP格式的灰度图,由于各球间相对位置不变,因此该转换不会引入额外误差。由球的边缘求取球心坐标,将球心的坐标投影到栅格量测空间中,并最终求得球心间的距离,实验结果如表1所示。
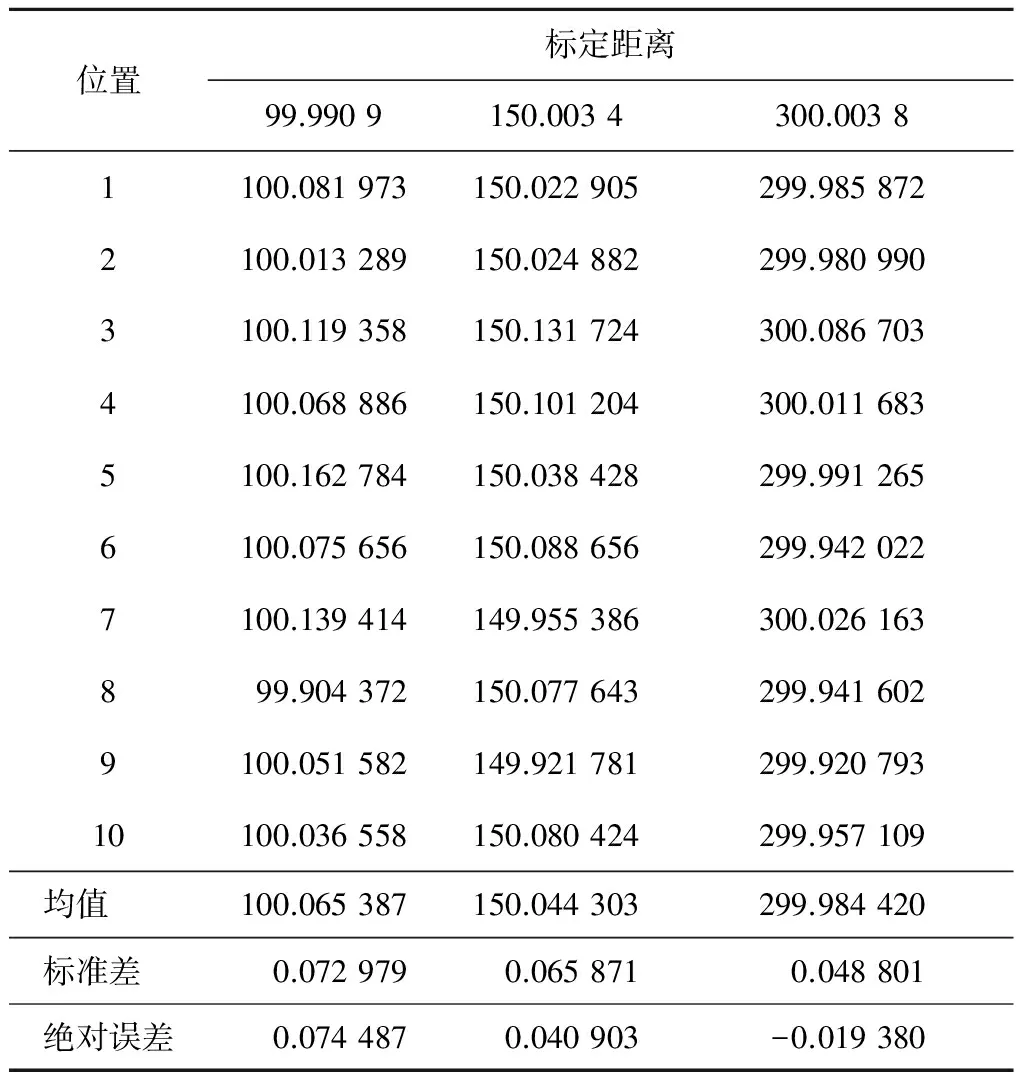
表1 实验结果mm
表1中的均值和标准差分别是在10组不同位置求得的球心间距离的均值和标准差,绝对误差为均值与标定距离的偏差。
4 结论
为提高近景摄影测量精度,本文提出了栅格空间量测法,利用摄影背景中的标定点建立了栅格量测空间,将物点通过其像点对应到栅格量测空间中进行测量。该算法简单有效地解决了拍摄中相机主距不同、相机倾斜、标定点本身不准确等误差源所导致的问题,而且避免了其他传统量测算法计算过程繁琐的问题。实验数据表明:本文所采用算法的精度已控制在忽米级。
[1] 高昭良.基于多基线数字近景摄影测量的滑坡检测系统研究[J].城市勘测,2015(2):5-6.
[2] 王之卓. 摄影测量原理[M]. 武汉:武汉大学出版社,2007:487-505.
[3] 冯文灏,王有年. 近景摄影测量的现状与展望[J]. 测绘通报,1988(3):15-22.
[4] 张祖勋.从数字摄影测量工作站(DPW)到数字摄影测量网格(DPGrid)[J]. 武汉大学学报: 信息科学版, 2007, 32(7):
565-571.
[5] 汪磊.数字近景摄影测量技术的理论研究与实践[D].郑州:中国人民解放军信息工程大学,2002.
[6] 张剑清,柯涛,孙明伟,等. 并行计算在航空摄影测量中的应用与实现:数字摄影测量网格(DPGrid)并行计算技术研究[J]. 测绘通报,2008(12):11-14.
[7] 郭琼林.数字近景工业摄影测量关键技术研究与应用[J].硅谷,2014(8):44-45.
[8] 张永军,王博,陈奇,等.近景摄影测量标志中心的自动提取算法[J].同济大学学报,2014,42(8):1261-1263.
[9] 张建霞,田保明,宋兆斌.基于Canon-5D相机的高精度近景摄影测量研究[J].测绘技术装备,2014,16(4):5-6.
[10] 苏新勇.数字近景工业摄影测量中编码标志点识别与检测技术的研究[D].淄博:山东理工大学,2014.
[11] 魏永华. 非正交基上的直接线性变换[J]. 测绘学报,1989,18(3):198-203.
[12] 林君建,苍桂华. 摄影测量学[M]. 北京:国防工业出版社,2006:178-182.
[13] 吴庆忠. 平行摄影测量的原理及应用[J]. 测绘通报,2001(12):12-13.
[14] 黄以东,李锦成. 数字近景摄影测量的试验[J]. 测绘学报,1988,17(2):93-100.
(责任编辑:尚彩娟)
Grid Space Measuration Based on Close-range Photography
XU Wan-li, BAO Shuo, LIU Yu-jun
(Department of Information Engineering, Academy of Armored Force Engineering, Beijing 100072, China)
Aiming at the problems in close-range photography that traditional photogrammetry has higher error and complicated calculation process, this paper presents a new photogrammetry called grid space measuration, which constructs an ideal grid measuring space directly by the image point from the calibrated point, then makes the interested physical point maps to the grid measuring space through its image point, finally gets its location value by fusion according to the distance with the grid data. Finally the experimental result shows that the error can be controlled within centimillimeter level by using this algorithm, the positioning precision is superior to the traditional algorithm, and the calculation is simple.
close-range photogrammetry; grid measuring space; grid space measuration; error control
1672-1497(2015)04-0080-03
2015-01-26
徐万里(1960-),男,教授。
P234.1
A
10.3969/j.issn.1672-1497.2015.04.016

