基于双层Bayes分析的3维编织复合材料弹道侵彻异常点检验

宫 雷, 许世蒙, 李春洋, 杜建华, 马润波

(1. 装甲兵工程学院基础部， 北京 100072； 2. 装甲兵工程学院技术保障工程系， 北京 100072； 3. 装甲兵工程学院科研部， 北京 100072)

基于双层Bayes分析的3维编织复合材料弹道侵彻异常点检验

宫 雷1, 许世蒙1, 李春洋2, 杜建华3, 马润波1

(1. 装甲兵工程学院基础部， 北京 100072； 2. 装甲兵工程学院技术保障工程系， 北京 100072； 3. 装甲兵工程学院科研部， 北京 100072)

在3维编织复合材料的弹道侵彻测试数据异常点检验中，将仿真数据作为试验数据的先验信息，采用Bayes方法检验模型形式和参数:应用2步估计方法推导出关键参数的后验分布，应用小概率判别法检验出异常点。数据统计分析结果表明：综合仿真数据与试验数据提供的信息，采用双层Bayes分析法检验异常点是行之有效的。

异常点；双层Bayes分析；3维编织复合材料；先验分布

3维编织复合材料弹道侵彻测试数据分析中的异常点是指与数据集的主体存在一定偏差的点[1]，如果这些异常点被忽视或处置不当，将会影响分析结果的准确性和有效性，甚至得到与实际情况严重不符的结果。传统弹道测试数据异常点的诊断主要采用基于统计、基于偏移、基于距离、基于密度等方法[2-3]，但在小样本、非重尾情况下，某些测量值与异常点表现非常类似，判断其是小概率事件还是较大概率事件，是常态还是偶发态，是正常点还是异常点等，很多问题亟待解决。

通过现代仿真技术可较为真实地描述系统的运行、演变及其发展过程，生成的仿真数据可作为试验数据的先验信息。而Bayes方法可充分利用先验信息，并综合样本信息进行Bayes统计推断[4]。本文将Bayes分析引入异常点判别中，将仿真数据作为试验数据的先验信息，并与试验数据有机结合，以此来检验试验数据中是否存在异常点，为3维编织复合材料的弹道侵彻测试数据异常点分析提供了一种使用少量试验数据便可高精度判别异常点的方法。

1 双层Bayes分析

1.1 异常点产生的原因

应用Bayes方法检验异常点时，产生异常点主要有如下3个原因。

1) 模型使用不当导致的数据异常。此处的模型使用不当是指数据分析时模型形式的选择不当。数学模型是用字母、数字及其他数学符号建立起来的等式或不等式，以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达式[4]，如线性模型、指数模型、非参数模型等。实践中，由于人们对现实问题理解的偏差和对数学知识的误用，应用模型时都会或多或少、直接或间接地导致数据表现异常。

2) 先验分布应用错误导致的数据异常。原则上讲，任何分布都可作为未知参数的先验分布[5]，但无论选用何种先验分布，最后都要看Bayes统计推断的效果。最常用的参数先验分布是无信息先验分布与共轭先验分布,其中：无信息先验分布基于同等无知原则；共轭先验分布的优点是未知参数的先验分布与后验分布属于同一分布族。在实际应用中，选取先验分布时应对所考察的事件有较为透彻的了解，这样才能使确定的先验分布更符合实际需求。若无信息先验分布选择不正确，会导致先验信息运用不当，进而浪费对目标已有的正确认识；应用共轭先验分布常犯的错误是过于重视计算的方便性而忽略先验的合理性[5-6]。

3) 模型中参数使用错误导致的数据异常。参数估计的核心是根据样本估计总体分布的未知参数。在新材料研发中，由于试验条件等因素的限制，有关新材料的数据严重缺失，需要应用仿真数据来估计模型参数，而这些参数是否适用于试验数据模型还需要进一步验证。

1.2 检验步骤

利用双层Bayes方法检验3维编织复合材料试验数据中异常点的步骤如下。

1) 模型形式检验。设试验数据集为(Y,X)。仿真数据分析表明Y与X间的关系服从某一经验模型，但该模型是否适用于试验数据，还需进一步分析。采用Bayes方法检验模型的思路是：求出每个数据点适用于仿真数据模型的后验概率，若后验概率很小的数据点足够多，则认为该模型不适用于试验数据[5]。实践中多采用比较分析法，即首先以试验数据为样本点导出其模型形式，并与经验模型形式相比较，若二者形式一致，则不需要重新建模，进入步骤2)；否则，重新分析机理，进一步了解研究对象的性质，修正经验模型。

2) 先验分布确定。由于模型参数多且相互关联，参数先验分布的确定较为困难，且即使能得出参数的先验分布，某些参数的先验分布对实际问题的作用也不大，因此确定参数先验分布时，应首先从实际问题出发，选择关键参数，然后再确定其先验分布。Box等[6]提出了确定参数先验分布的最佳方法：首先,主观估计出参数先验分布的几个分位数；然后,选择合适的先验分布密度形式，并依据极大似然法计算超参数。

3) 模型参数确定。在Bayes决策问题中，表示未知参数点估计的决策函数称为未知参数的Bayes估计，其与损失函数密切相关：若已知未知参数的先验分布，则Bayes估计在平方损失下，为其后验分布的均值；在绝对损失下，为其后验分布的中位数；在0-1损失下，为其后验极大似然估计[7]。

采用Bayes方法检验异常点的流程如图1所示。

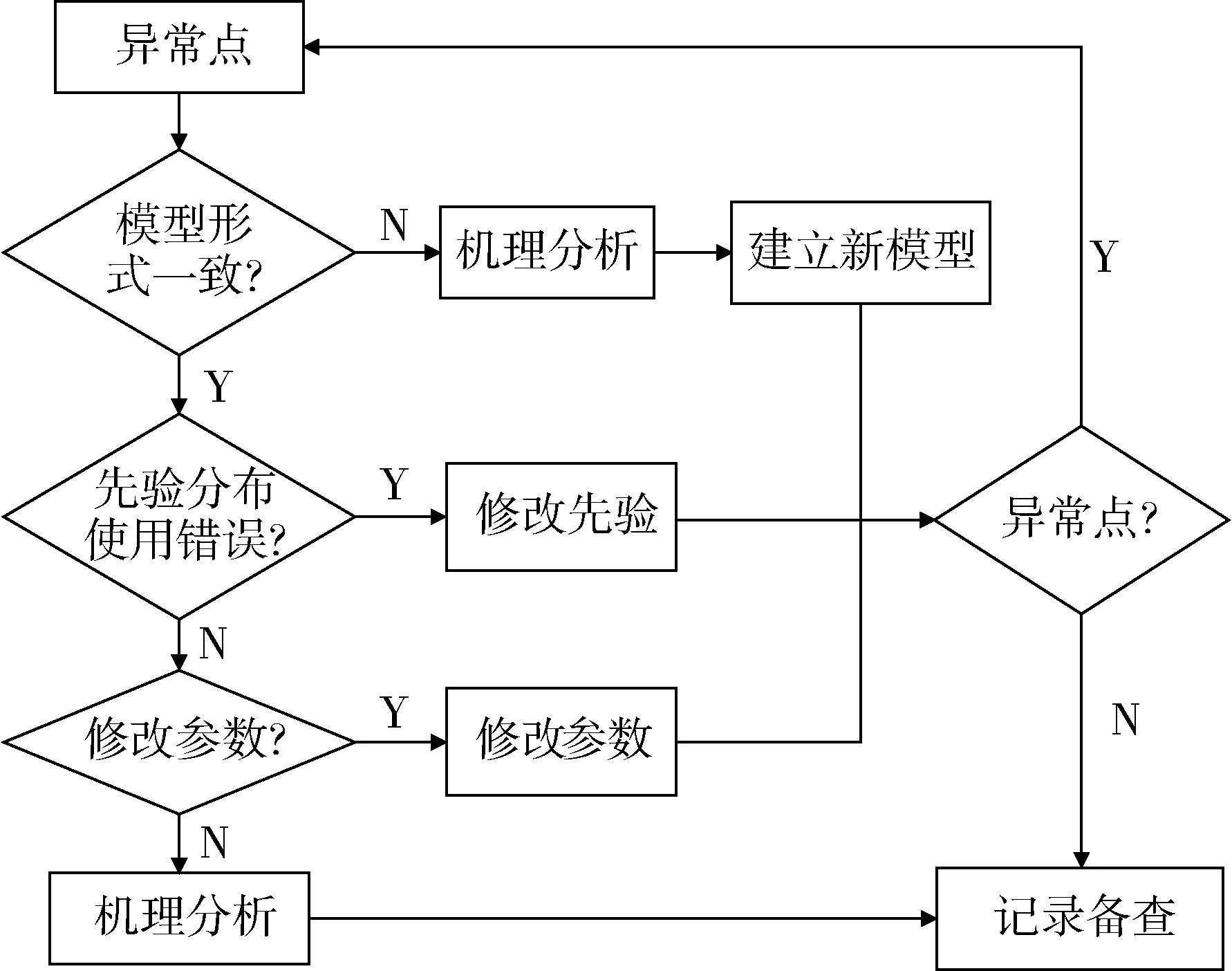
图1 Bayes方法检验异常点的流程

2 实例分析

2.1 试验设计与测试结果

试验[8]采用的纤维材料为荷兰Tarpon 1000型、对位芳族聚酞胺纤维长丝束合股，基体为热固性环氧树脂，采用纵横阵列编织机进行织造；发射采用7.62 mm步枪标准弹，56式弹道发射枪；用2组锡箔作计时触发器，共测试13组子弹的入射速度与剩余速度，结果如表1所示。

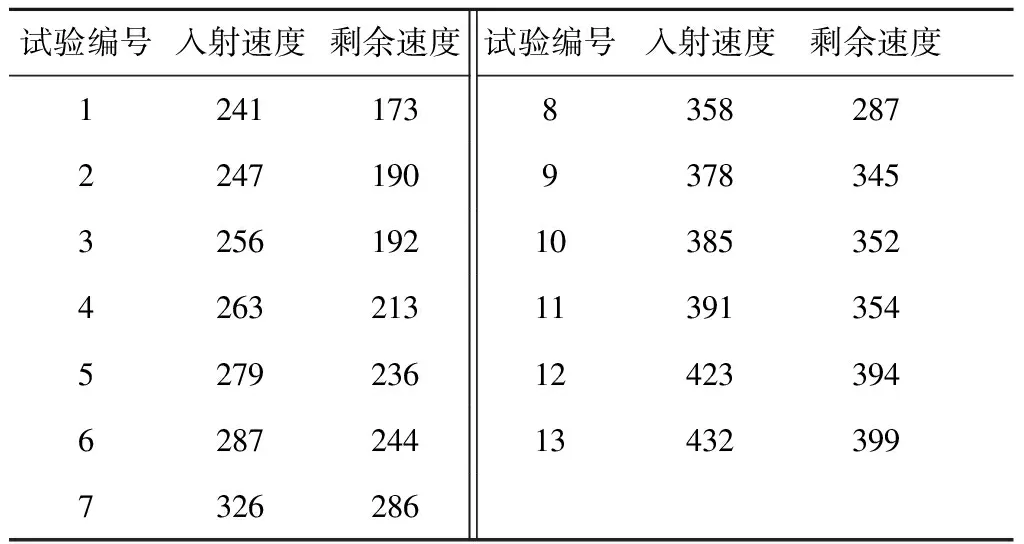
表1 3维编织复合材料弹道侵彻试验入射速度与剩余速度的测试结果 m/s

2.2 异常点分析

2.2.1 模型形式

练军[8]在考察3维编织复合材料细观结构的基础上，建立了与3维编织复合材料具有相同纤维体积的单向板细观模型，通过精细化标准细观结构模型与细观结构模型的弹道侵彻破坏过程的有限元分析，揭示了3维编织复合材料在弹道冲击下的破坏模式，计算出弹体贯穿靶体后的剩余速度，这些仿真数据可信度高，对判断试验数据中的异常点极具借鉴意义。仿真数据分析表明：3维编织复合材料弹道侵彻试验中，剩余速度与入射速度应呈线性关系。

图2为3维编织复合材料弹道侵彻试验数据中剩余速度对入射速度的散点图。

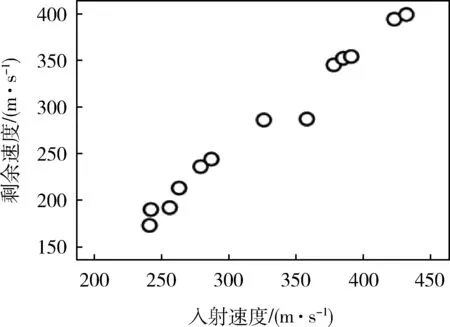
图2 3维编织复合材料弹道侵彻试验中剩余速度对入射速度散点图

由图2可以看出：剩余速度与入射速度的线性关系显著，且剩余速度随着入射速度的增大而增大。此判断与仿真数据分析结果一致，因此，在3维编织复合材料弹道侵彻试验数据分析中可不改变模型形式，将采用一元线性回归模型来刻画剩余速度与入射速度的关系，即

Y=βX+ε,

(1)

式中：Y为剩余速度；X为入射速度；ε～N(μ0,σ02)，为误差。

2.2.2 参数先验分布

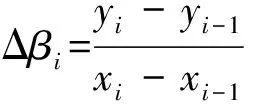
1) Δβi近似服从正态分布，即Δβi～N(μ,σ2)，其中：μ、σ2均未知，且相互独立。

2)μ在1.134附近取值的概率大，μmin=0，但接近0的概率极小，μ的概率密度函数为钟形曲线。

由此可认为：μ的先验分布π(μ)为正态分布，即π(μ)～N(μ1,σ12)。根据3-σ法则，设1.134-3σ1=0，可得σ1=0.378，则π(μ)～N(1.134,0.3782)。

2.2.3 模型参数的Bayes估计

在试验数据中，Δβ=X～N(μ,σ2)，即

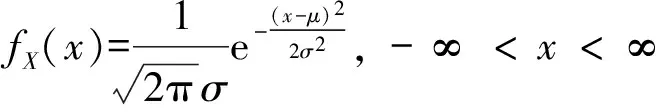
采用2步估计法估计模型参数。

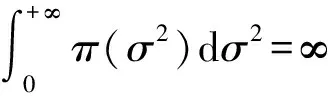
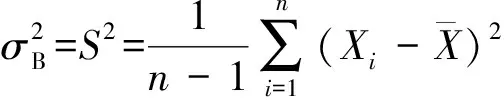
(2)

2) 估计μ。未知参数μ的先验分布为π(μ|σ2)～N(μ1,σ12)，根据文献[4]，在方差已知的前提下，若正态总体均值的先验分布为正态分布，则在平方损失、绝对损失、0-1损失下，未知参数Bayes估计μB均为后验均值[13-15]， 即

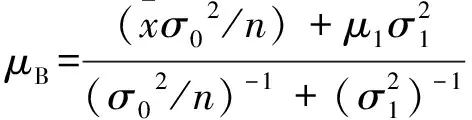
(3)

2.2.4 异常点检验

3维编织复合材料弹道侵彻试验中剩余速度对入射速度的变化率如表2所示。

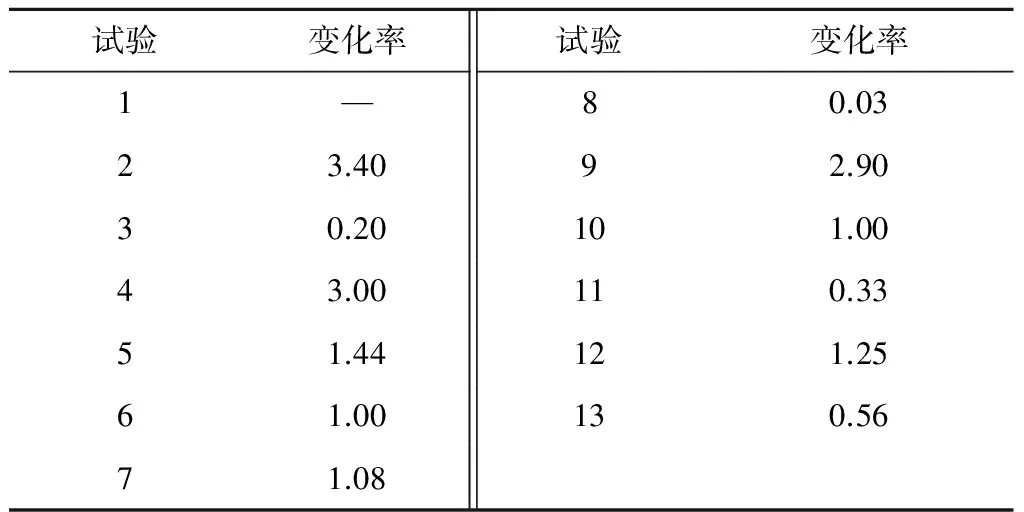
表2 3维编织复合材料弹道侵彻试验中剩余速度对入射速度的变化率

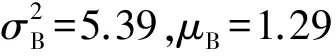
|P{μ<3.40}-P{μ0≥3.40}|=0.94，

|P{μ<3.00}-P{μ0≥3.00}|=0.87，

|P{μ<0.03}-P{μ0≥0.03}|=0.71，

|P{μ<2.90}-P{μ0≥2.90}|=0.85，

由此可知：2、4、9号数据点可怀疑为异常点；8号数据点虽然不超过显著性水平0.85，但由于显著性水平较高，也是值得关注的数据点，实践中可结合其他方法来复检其异常性；其余数据点均为非异常点。

3 结论

1) 双层Bayes方法在检验模型形式和参数时均采用Bayes方法，将仿真数据处理为先验信息，有效实现了仿真数据与试验数据的信息融合，从而通过少量试验数据便可挖掘出更多信息，且具有很好的精度。

2) 试验设计时不应采用入射速度相差不大的数据点；否则，易导致Δβi偏大，从而将由样本数据的随机性产生的数据点误判为异常点。

3) 采用数据点的变化率来检验异常点，会存在1个数据异常点带动其前后2个非异常点显示异常的情况，因此，应用双层Bayes方法检验异常点时应考虑与其他方法相结合。

4) 为了更好地探索3维编织复合材料弹道侵彻数据的规律性，应结合试验设计来研究异常点的分析方法。

[1]HawkinsD.IdentificationofOutliers[M].London:ChapmanandHall, 1980:1-58.

[2]BarnettV,LewisT.OutliersinStatisticalData[M].NewYork:JohnWiley, 1994:72-134.

[3]VelascoF,VelmaP.ImportanceofSleeknessandKurtosisStatisticalTestsforOutlierDetectionandEliminationinEvaluationofGeochemicalReferenceMaterials[J].MathematicalGeology, 1998, 30(1): 109-128.

[4]MeerschaertMM.数学建模方法与分析[M].刘来福，杨淳，黄海洋，译. 北京：机械工业出版社, 2007:1-24.

[5] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京：高等教育出版社, 2006:307-391.

[6]BoxGEP,TiaoGC.ABayesianApproachtoSomeOutlierProblems[J].Biometrika,1988, 55(3):119-129.

[7]BergerJO.统计决策论及贝叶斯分析[M].贾乃光，译.北京：中国统计出版社, 2006:59-128.

[8] 练军.三维编织复合材料弹道侵彻的数值模拟[D].上海：东华大学, 2006.

[9] 陈玲. 线性模型中参数型经验Bayes估计若干问题研究[D].合肥：中国科学技术大学,2011.

[10] 宫雷,许世蒙,杜建华,等. 3维编织复合材料弹道测试数据的异常点分析[J]. 装甲兵工程学院学报,2014,28(5):94-97.

[11] 韦来生,张伟平.贝叶斯分析[M].合肥：中国科学技术大学出版社, 2013:33-80.

[12] 丁晓,韦来生. 双指数分布位置参数的经验Bayes估计问题[J]. 数学杂志,2005,33(4):413-420.

[13] 杨亚宁.正态分布参数的经验Bayes检验[J].中国科学技术大学学报,1992,22(1):12-21.

[14] 刘荣玄,朱少平. 正态模型刻度参数的经验贝叶斯估计的渐近性[J]. 统计与决策,2009, 18(17):158-160.

[15] 仇丽莎,韦来生. 正态总体均值和误差方差同时的经验Bayes估计[J].中国科学院大学学报,2013,30(4):454-461.

(责任编辑: 王生凤)

Outliers Test of 3D Braided Composite’s Ballistic Data Based on Double Bayesian Analysis

GONG Lei1, XU Shi-meng1, LI Chun-yang2, DU Jian-hua3, MA Run-bo1

(1. Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing 100072, China; 2. Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 3. Department of Science Research, Academy of Armored Force Engineering, Beijing 100072, China)

In the outliers test of 3D braided composite’s ballistic penetration test data, taking the simulation data as the prior of experimental data, Bayes method is adopted in the test of model and parameters, the method of two-step estimation is used to deduce posterior distribution of key parameter, and the outliers is examined by the little probability discriminant method. The data statistical analysis result shows that it is an effective method to test the outliers with the double Bayesian analysis method using the information provided by simulation data and experimental data.

outlier; double Bayesian analysis; 3D braided composite; prior distribution

1672-1497(2015)04-0107-04

2015-04-07

国家自然科学基金资助项目(51001117)； 北京自然科学基金资助项目(3132024)

宫 雷(1980-)，男，讲师，硕士。

O21

A

10.3969/j.issn.1672-1497.2015.04.022