履带车辆转向过程载荷的统计分析

李善乐， 王红岩， 芮 强， 王钦龙， 郭 静

(1. 装甲兵工程学院机械工程系， 北京 100072； 2. 中国北方车辆研究所车辆传动重点实验室，北京 100072)

履带车辆转向过程载荷的统计分析

李善乐1， 王红岩1， 芮 强1， 王钦龙1， 郭 静2

(1. 装甲兵工程学院机械工程系， 北京 100072； 2. 中国北方车辆研究所车辆传动重点实验室，北京 100072)

为研究履带车辆在随机环境下的行驶载荷，利用解析法和响应面相结合的方法,建立了履带车辆转向载荷替代模型，并采用蒙特卡洛抽样方法,分析了统计情况下车速、摩擦因数和行驶阻力系数对驱动力矩和制动力矩的影响，最后通过实车试验对计算结果进行了统计验证。结果表明：计算结果与试验结果统计分布一致，证实了所提方法的科学性，为履带车辆在复杂随机环境下行驶载荷的统计计算提供了新的途径。

履带车辆；统计特征；转向运动；响应面模型

目前，国内外学者[1-2]对履带车辆的研究大都是基于Wong[3]建立的履带车辆稳态转向模型，主要考虑履带与地面之间在剪切作用下的滑转、滑移、质心和几何中心不重合以及高速时离心力条件下的转向模型。上述研究工作中都引入了行驶阻力系数和摩擦因数等环境变量，求解时将这些地面环境参数作为确定量来考虑，计算结果只是某一特殊情况，不能全面反映履带车辆的实际运行状况。为了研究履带车辆在随机环境下的行驶载荷，笔者采用转向载荷解析法和响应面相结合的方法构建随机环境下转向载荷替代模型，并进行了实车试验验证。

1 履带车辆转向过程分析与建模

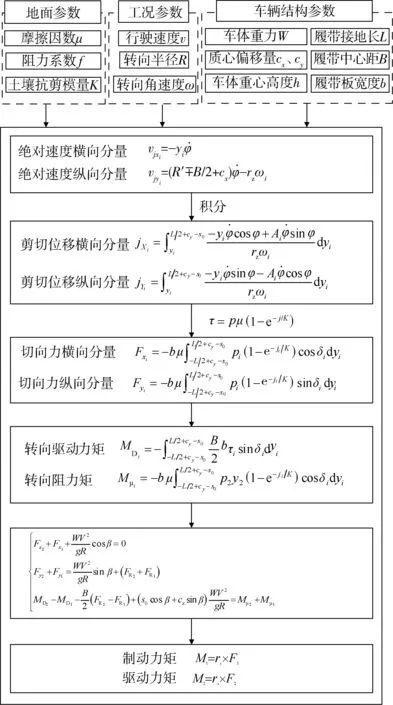
图1 履带车辆转向模型框图

图2为车辆转向模型的迭代求解流程，可以看出：履带车辆转向过程的求解是在给定车辆结构参数、行驶速度、转向半径的基础上，对转向极偏移量A1、A2、A3赋初值，然后代入图1所示的模型方程中进行求解得到的。

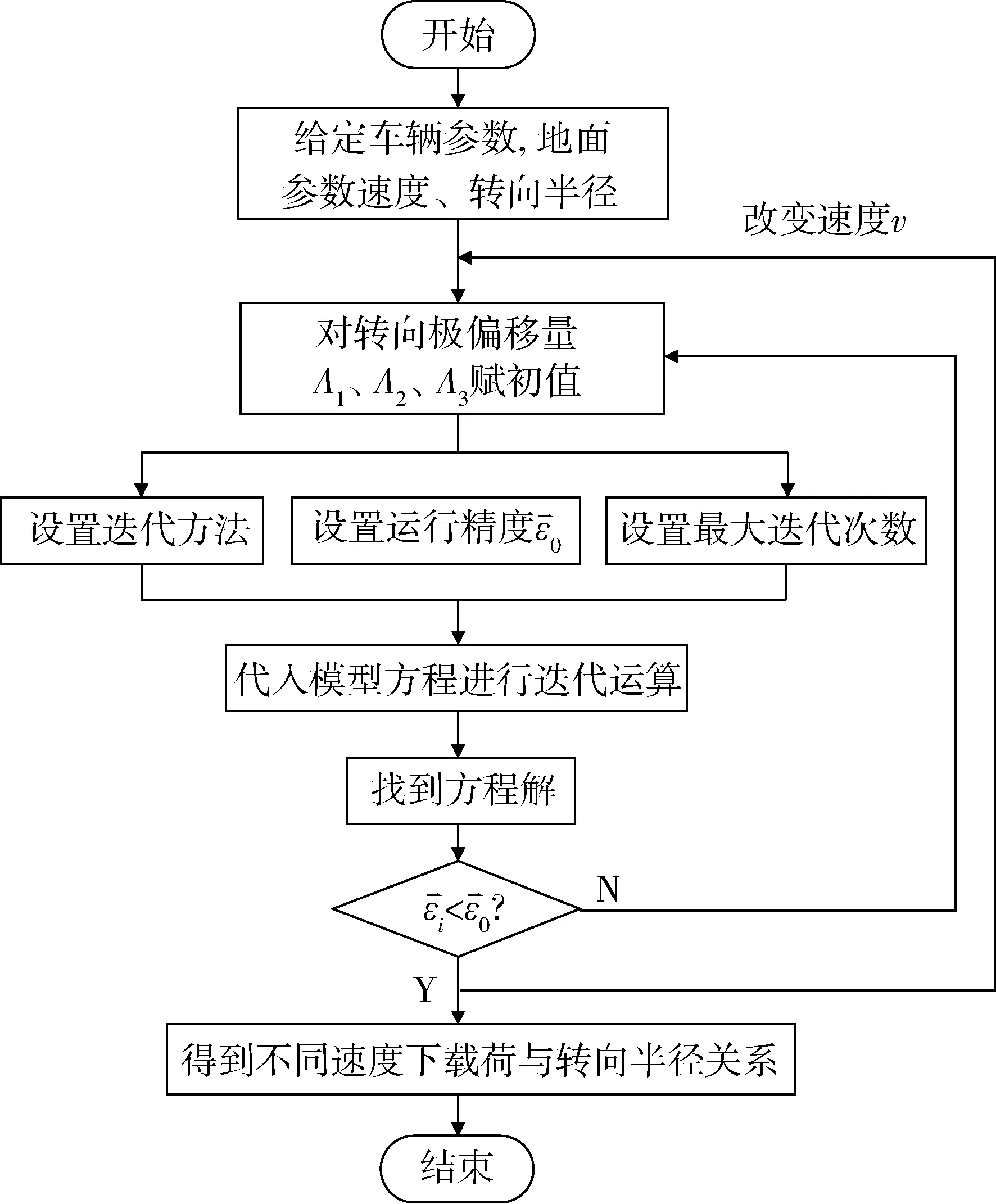
图2 转向模型解算流程

2 行驶地面和工况参数的统计模型

2.1 履带车辆地面参数的统计

履带车辆实际行驶的环境极其复杂，包括行驶阻力系数、摩擦因数等多种不确定性因素。大量的统计数据表明：这些随机变量服从一定的分布规律[7]。根据计算模型的需要，给出几种典型路面类型参数的统计特征值，如表1所示。

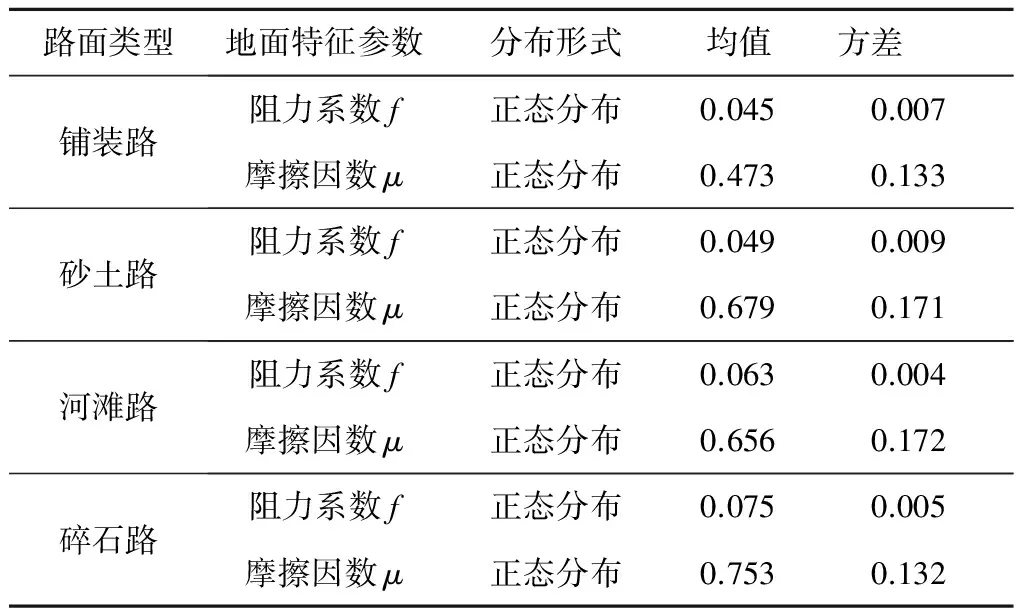
表1 不同路面类型特征参数

2.2 履带车辆行驶工况统计

以某型履带车辆在不同路面上进行的实车转向试验获得的数据为基础，通过对行驶速度进行统计，得到其速度分布的概率密度函数，如图3所示，对应的概率密度函数特征参数如表2所示。

图3 不同路面行驶速度的概率密度函数

表2 不同路面转向行驶速度统计分布的特征参数

路面类型速度统计分布的特征参数值均值u/(km·h-1)方差铺装路16．183．94砂土路11．683．16河滩路9．332．45碎石路7．791．90

3 转向载荷替代模型的建立及结果分析

3.1 转向载荷替代模型的建立

履带车辆运动过程中的载荷与行驶工况和地面环境有关。当转向模型中的地面参数和工况参数为随机变量时，若采用如图1、2所示的解算过程，则存在规模大、计算周期长的问题。替代模型[8]是在不降低精度的情况下，采用少量样本点构造的计算量小、精度高的近似模型。因此，本文利用该模型代替原有的复杂模型进行分析。

3.1.1 测试样本点的设计

由于拉丁超立方[9]设计的样本点均匀地分布在整个设计空间，且每个因子水平只使用一次，能够使用较少的样本点反映整个设计空间的响应特性，因此本文选择拉丁超立方设计法。

在转向载荷模型中，影响载荷的参数有很多，这里选择对转向载荷影响较大的行驶速度、行驶阻力系数和摩擦因数为设计变量。根据拉丁超立方设计法进行取样，抽取30个样本点，最终得到的样本点分布如图4所示。

图4 参数的样本点分布

3.1.2 载荷替代模型的建立

以履带车辆在砂土路转向为例，用第1节中建立的转向模型解析法对采样的30个设计点进行计算，采用多项式响应面法建立替代模型，多项式响应面的一般形式为

(1)

式中：xp、xq为自变量；n为自变量个数；β0、βp、βpq为待定系数。

根据实验设计点的值及其响应，结合式(1)得到二阶多项式响应面模型。图5为f=0.05和μ=0.9时的响应面模型。通过检验可以得到：对于二阶响应面替代模型，制动力矩的复相关系数为0.956，驱动力矩的复相关系数为0.976，复相关系数接近于1，表明多项式响应面替代模型精度满足使用要求。

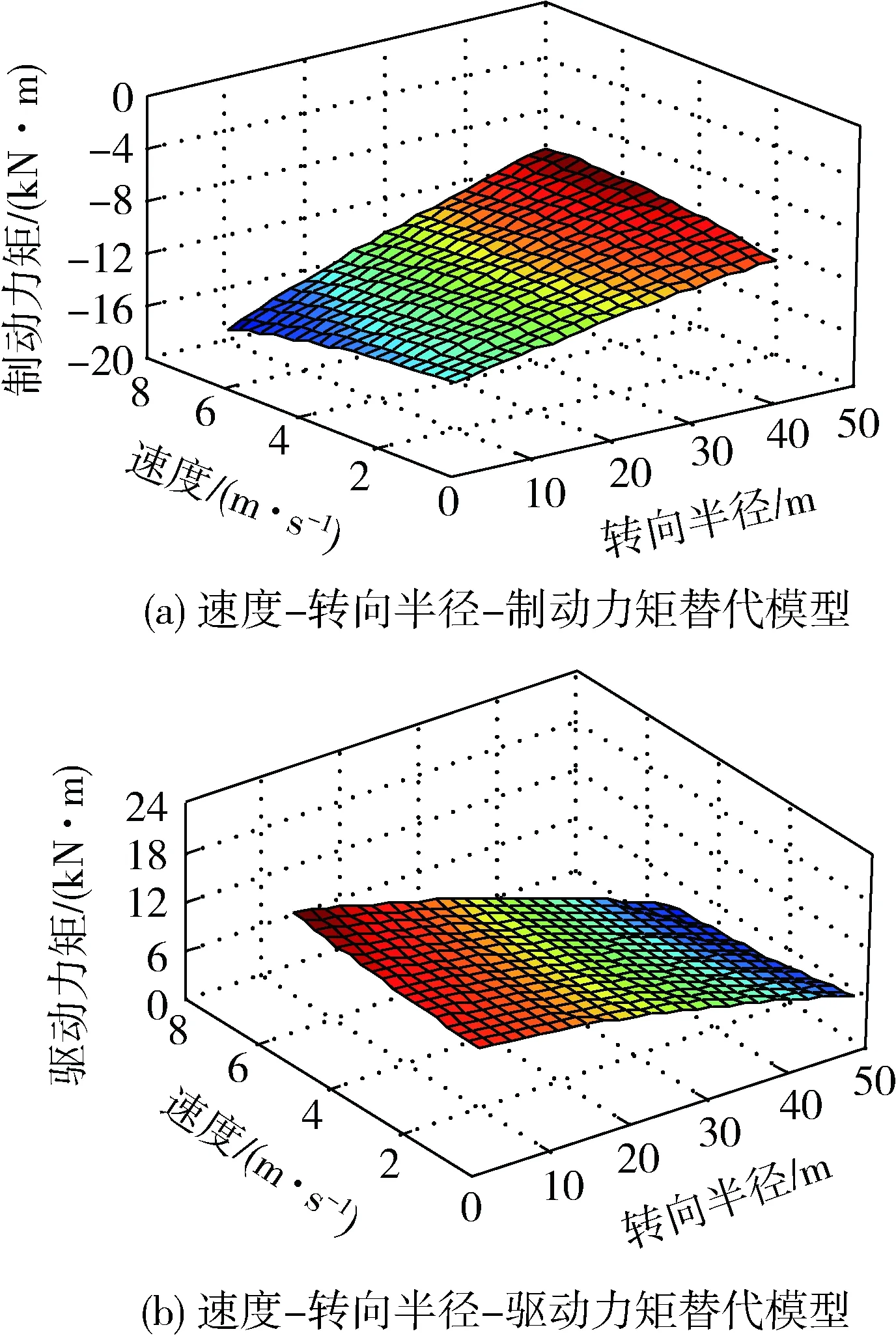
图5 二阶多项式响应面载荷替代模型

3.2 计算结果分析

3.2.1 转向速度对载荷的影响

图6(a)为f=0.05和μ=0.9时，速度按照正态分布进行1 000次蒙特卡洛抽样计算得到的主动轮轴的驱动力矩、制动力矩与转向半径的关系曲线。可以看出：1)转向力矩载荷随着转向半径的增大而减小，这与常规的计算和试验测试结果一致[1-2]；2)转向速度对载荷的影响在一定的范围内呈分散状态，在半径较小时，转向速度使载荷分布的范围变宽，随着转向半径的增大，转向速度对转向载荷分布的影响减小。图6(b)为相应的两侧主动轮轴驱动力矩、制动力矩分布的概率密度曲线，可以看出驱动力矩、制动力矩的离散程度以及概率密度分布情况，其不同颜色反映了概率密度的大小。

图6 对速度抽样得到的曲线分布

图7为驱动力矩、制动力矩统计的直方图以及根据直方图拟合的分布，可以看出：驱动力矩、制动力矩很好地服从正态分布。

3.2.2 摩擦因数对载荷的影响

设摩擦因数服从正态分布，进行1 000次蒙特卡洛抽样计算，f=0.05和v=2 m/s时的驱动力矩、制动力矩与转向半径的关系曲线如图8(a)所示。可以看出：载荷在一定的范围内呈分散状态，在转向半径较小时，摩擦因数使载荷分布的范围变宽；随着转向半径的增大，摩擦因数对转向载荷分布的影响程度降低。图8(b)为相应的驱动力矩、制动力矩分布的概率密度曲线，可以看出：驱动力矩、制动力矩密度较大的区域基本分布在5～12 kN、-5～-12 kN附近，分别小于速度抽样时分布的范围。

图7 力矩分布直方图

图8 对摩擦因数抽样得到的曲线分布

对比图6(b)可以看出：1)对摩擦因数进行抽样时，转向载荷的较高概率密度范围更广，为10～50 m，这说明在整个转向半径范围内，履带与地面之间的摩擦因数对载荷都有较大的影响，这与实际情况相一致；2)当摩擦因数较小时，转向载荷随转向半径几乎没有变化，呈常量状态，这基本属于小概率事件。

3.2.3 行驶阻力系数对载荷的影响

对行驶阻力系数按照正态分布进行1 000次蒙特卡洛抽样计算，其μ=0.9和转向车速v=2 m/s时的驱动力矩、制动力矩与转向半径的关系曲线如图9(a)所示，可以看出：载荷在一定的范围内呈分散状态，且行驶阻力系数在整个半径范围内对载荷的影响较为一致。图9(b)为相应的驱动力矩、制动力矩分布的概率密度曲线，可以看出：1)力矩概率密度较大的区域基本分布在整个转向半径范围内；2)在相同半径下，载荷的分布变化范围明显小于对行驶速度和摩擦因数抽样计算时得到的力矩的分布变化范围。

图9 对行驶阻力系数抽样得到的曲线分布

从图6-9可以看出：1)履带车辆驱动力矩和制动力矩随转向半径进行变化，转向半径增大时，履带车辆的驱动力矩和制动力矩相应地减小；2)速度、摩擦因数和运动阻力系数统计分布会造成两侧力矩在较大范围内变化，这是由环境和运行工况参数的不确定性引起的；3)转向速度和摩擦因数对力矩的影响较大，而行驶阻力系数的影响较小，在以后的研究中可以不考虑行驶阻力系数对载荷的影响。

4 实车试验及结果对比分析

4.1 履带车辆转向性能试验

履带车辆实车转向性能试验测试装置如图10所示，其中：NI测试系统能够实现转向过程中两侧主动轮转速、车辆运行轨迹、行驶速度、航向角及综合传动装置两侧输出轴转速、转矩等数据的同步测试。

图10 实车转向性能试验测试装置

实车试验过程中，被测试车辆在砂土路连续进行不同半径的转向，GPS记录车辆转向轨迹，转速转矩测试装置记录转速和转矩，数字罗盘记录车辆的航向角，图11(a)为GPS记录的车辆行驶轨迹。由于测试车辆采用综合传动装置，主动轴力矩测量困难，因此需先测量传动系统输出轴的扭矩，再转化为驱动力矩、制动力矩，其传动系统扭矩测试结果如图11(b)所示。

4.2 试验结果和计算结果对比分析

利用Matlab软件对测得的试验数据进行处理，其结果如图12所示。为与理论计算结果对比，图中给出了计算结果在95%置信区间内的边界曲线，可以看出：1)当履带车辆在不同的速度与转向半径下转向时，由于实际环境参数和车辆运行工况的影响，驱动力矩、制动力矩在一定的范围内分布，并随着转向半径的增大而减小；2)试验测得的驱动力矩与制动力矩基本分布在计算结果的95%置信区间内，说明计算结果和试验结果具有很好的统计一致性。

图11 部分数据试验测试结果

图12 试验测试结果与计算结果的对比

图13为试验测得的驱动力矩、制动力矩分布直方图，可以看出：驱动力矩和制动力矩服从正态分布。表3为驱动力矩、制动力矩的统计规律以及与计算值的对比，可以看出：计算结果和试验结果的统计规律具有较好的一致性，都服从正态分布，误差较小，说明这种计算随机载荷方法是正确的。

图13 试验测得的力矩分布直方图

表3 计算结果与试验结果统计规律对比分析

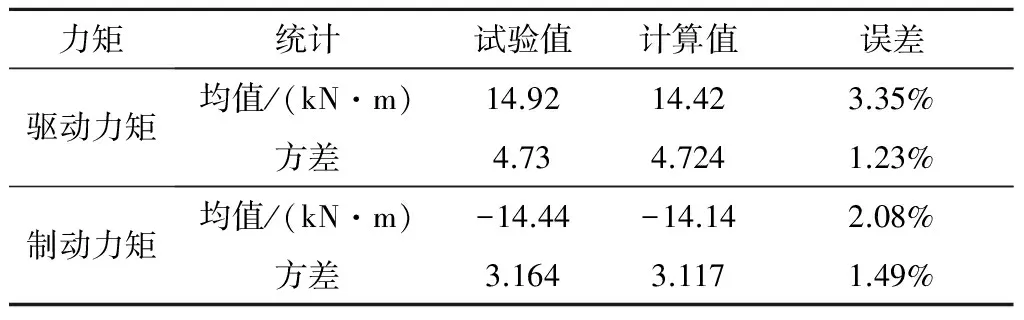
力矩统计试验值计算值误差驱动力矩均值/(kN·m)14．9214．423．35%方差4．734．7241．23%制动力矩均值/(kN·m)-14．44-14．142．08%方差3．1643．1171．49%

[1] Maclaurin B. Comparing the Steering Performance of Skid and Ackermann Steered Vehicles[J]. Automobile Engineering, 2008, 222(5):39-56.

[2] 王红岩，王钦龙，芮强,等.考虑履带滑动的转向过程的仿真与试验验证[J].装甲兵工程学院学报, 2014,28(2):31-35.

[3] Wong J. Theory of Ground Vehicles [M]. 3rd Edition. New York: John Wiley & Sons, 2001: 141-144.

[4] Said A M，Lakmal D S，Kaspar A. Track-terrain Modelling and Traversability Prediction for Tracked Vehicles on Soft Terrain[J]. Journal of Terramechanics，2010，47(3)：151-160.

[5] Wong J Y, Chiang C F. A General Theory for Skid Steering of Tracked Vehicles on Firm Ground[J].Journal of Automobile Engineering, 2001, 215(3): 343-355.

[6] 程军伟，高连华，王红岩,等. 履带车辆转向分析[J]. 兵工学报，2007，28(9)：1110-1115.

[7] 居乃鵕．装甲车辆动力学分析与仿真[M]．北京：国防工业出版社，2002：16-35.

[8] 龙腾，刘莉，孟令涛，等．基于代理模型的翼型多目标集成优化设计[J].系统仿真学报, 2010, 22(7): 1604-1608.

[9] McKay M D，Conover W J，Beckman R J． A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics, 1979, 21(2):239-245．

(责任编辑:尚菲菲)

Statistical Analysis on Loading of Tracked Vehicles in Steering Process

LI Shan-le1, WANG Hong-yan1, RUI Qiang1, WANG Qin-long1, GUO Jing2

(1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 2. Key Laboratory of Vehicle Transmission, China North Vehicle Research Institute, Beijing 100072, China)

To study the driving load of tracked vehicles in stochastic environment, a superseded model of steering loading is built by using response surface and analytic method. Based on this superseded model, effects of statistical vehicle velocity, friction coefficient and motion resistance coefficient on traction and braking torques by means of Monte Carlo are analyzed. A certain tracked vehicle is tested at last and testing results are statistically analyzed. The scientificity of the method are verified with the coincidence of the computing results and testing result, which puts forward a new way to calculate the driving loading in complex stochastic environment.

tracked vehicles; statistical characteristics; steering motion; response surface model

1672-1497(2015)04-0040-06

2015-06-02

军队科研计划项目

李善乐(1991-)，男，硕士研究生。

TJ811

A

10.3969/j.issn.1672-1497.2015.04.009