基于Morris方法的车轴结构参数灵敏度分析*

□ 胡国标 □ 邹益胜 □ 姜 杰 □ 李成浩

西南交通大学机械工程学院 成都 610031

高速列车的运营环境比较恶劣［1］，车轴作为高速列车转向架的关键承载部件之一，其强度直接决定着高速列车的运行安全。为了保证列车运行安全，指导车轴结构优化设计，研究影响车轴强度的关键结构参数具有重要意义。全局灵敏度分析方法是研究系统参数对系统响应或输出影响度的有效方法，对车轴进行灵敏度分析，求得关键设计参数对车轴强度的影响，可以为优化车轴结构、提高车轴性能提供基础依据。一直以来，全局灵敏度分析方法在结构分析与优化领域中得到了广泛应用。杨大彬等［2］应用 ANSYS对一个Schwedler型单层球面网壳建立了仿真计算模型，然后采用Spearman秩相关系数法对其进行了灵敏度分析，得出了几种结构响应对于不同位置杆件的截面平均半径的灵敏度值。尹俊杰等［3］首先利用支持向量机建立了飞机整体翼梁结构ANSYS仿真计算的替代模型，在此基础上采用Sobol法对飞机整体翼梁结构的界面参数进行了全局灵敏度分析，识别了飞机整体翼梁结构的损伤容差关键参数。李彬［4］为了探讨纤维复合材料结构固化成型过程中固化工艺温度、热传导系数、对流换热系数等参数对固化均匀性的敏感程度，采用了Morris方法定量分析几个关键参数对复合材料固化均匀性的影响程度，得到了影响因素按灵敏程度由大到小的排序。

基于ANSYS的车轴非线性仿真计算速度缓慢，不适宜使用需要大量样本数据作计算支撑的Sobol法。相对而言，Morris方法能够以较少的计算代价，获得参数全局灵敏度的比较以及参数相关性定性描述，对于有大量参数的模型或者计算时间较长的模型效率较高。因此本文提出了基于Morris方法的结构灵敏度分析流程，并以某型车车轴为实例，利用Morris方法计算得到车轴结构设计参数的灵敏度，该结果对车轴的结构设计及优化具有一定的指导意义。

1 基于Morris方法的灵敏度分析流程

Isight软件是由Engineous公司开发的一套可整合设计流程中所使用的各项软件的工具，为实现灵敏度分析过程中试验采样的自动化，笔者在Isight软件的集成环境下提出如图1所示的灵敏度分析流程。

▲图1 基于Morris方法的灵敏度分析流程

（1）利用基于MATLAB编写的Morris方法试验设计程序生成矩阵表，提交给Isight进行DOE样本采集。

（2）Isight集成ANSYS仿真计算程序，读取第一步中生成的试验设计表并驱动ANSYS仿真程序进行计算，得出采样结果。

（3）用MATLAB程序读取由第二步完成的DOE采样结果，计算得出灵敏度分析结果。

2 Morris方法原理

Morris方法最初由Max D.Morris在1991年提出［5］，是基于参数空间的离散搜索方法，能在全局范围内研究模型参数。其主要思想是假定衡量参数xi灵敏程度的“基本因素（EE）”服从某种分布fi，测量该分布的均值和标准差即可确定参数的全局灵敏度。如果参数xi所对应的均值越大，则表明其对模型输出的影响越大［5,6］。标准差σ则被用来衡量参数之间的交互作用，其值越大，表明该参数与其它参数的交互作用越大，反之越小。

对于一个包含k个参数的模型，假设参数的变化范围为［0,1］，采用Morris采样法随机生成一组初始参数向量 X=（x1，x2， …，xk）， 其中 xi的值由 ｛0，，...，1-Δ｝中随机抽取，p为参数范围空间内划分的个数，Δ为预先设定的变化量，Δ的取值为：

则第i个参数的基本因素的计算公式为：

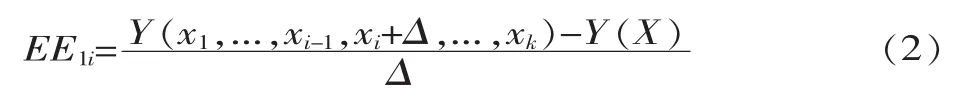
式中：Y（X）为初始参数向量对应的模型输出，Y（x1，...，xi-1，xi+Δ，..，xk）为初始参数向量的第 i个参数产生变化量Δ后对应的模型输出。

对于剩下的k-1个参数，重复上述操作，分别对剩下的k-1个参数计算其基本因素，随机生成n个初始向量，重复上述过程可以分别计算出k个参数的n个基本因素 EEij,其中 j=1，2，...，n，i=1，2，...，k。 每个参数的基本因素的均值μ与标准差σ可表示为：

3 车轴结构参数灵敏度分析

以某型车车轴为例，考虑在某一特定工况下，车轴各个轴段半径大小的变化对其在服役环境中所受最大应力值的影响，车轴截面如图2所示。

▲图2 车轴截面图

该车轴为阶梯空心轴，共由11段组成，其中车轴在第3、9段处分别与左右车轮装配，在第6段处与齿轮箱装配。轴段 1、2、3 分别与轴段 11、10、9 对称。根据装配要求，轴段6的半径应当大于轴段5、7的半径，轴段3的半径大于轴段1、2、4的半径，轴段9的半径大于轴段8、10、11的半径。各轴段半径参数及相关关系见表1。

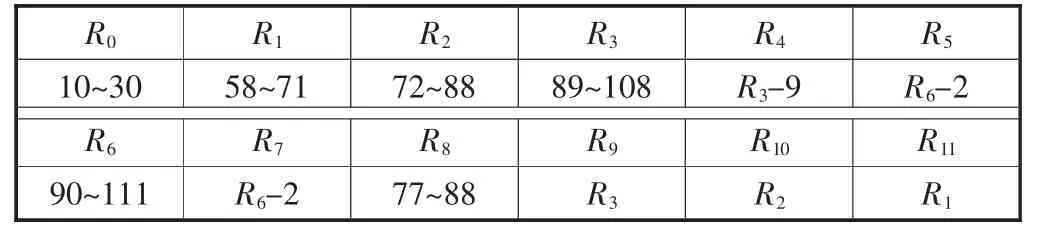
表1 各轴段半径参数表/mm

3.1 车轴有限元分析模型建立

车轴强度的分析参照了EN 13104标准 《铁路行业/轮对和转向架/驱动车轴结构设计和计算方法》，并基于ANSYS的APDL语言编写了仿真计算程序。车轴是变截面承载结构，为了精确计算车轴在各种载荷下的应力分布，且考虑轮轴过盈配合对车轴强度的影响，仿真计算中采用Solid185六面体单元进行划分，并采用Target170和Contact174单元模拟过盈配合。车轴在服役过程中，承载的主要运营载荷分为以下3种：①簧上质量产生的静载荷、动载荷和簧下集中质量振动产生的动载荷；②基础制动产生的载荷；③ 驱动系统产生的载荷。

簧上簧下质量产生的载荷可由标准中的计算公式计算得到，基础制动和驱动系统产生的载荷为已知确定载荷。为了精确计算车轴的强度，在轴颈处模拟轴承施加水平和垂向约束，在轴肩处施加轴向约束，在车轮底部按照标准施加垂向载荷和横向载荷，模拟轮轨作用力，为模拟过盈力，在车轮和车轴配合处添加过盈配合约束［7-10］。建立的车轴有限元分析模型如图3所示。

按照静强度评定标准，在有限元分析计算完成后，利用APDL语言提取了车轴最大VON Mises应力作为评价指标。

3.2 Morris采样

由于手动更改模型参数进行取样的方式效率低下，本文在Isight环境下集成ANSYS仿真计算程序，通过Isight不断驱动更改仿真模型参数，并执行计算的方式实现采样自动化。Isight中实现流程如图4所示。

由车轴各个轴段半径相关关系可知，整个车轴轴段半径参数可归纳为 6 个自由变量：R0、R1、R2、R3、R6、R8。根据Morris采样方法，k为变量数目，在本实例中取值为6。本文将参数范围空间统一划分成5等份，即p取值为5，且令每个参数的基本因素计算8次。根据以上参数的设定生成Morris试验设计表，Isight驱动DOE组件读取Morris试验设计表并驱动ANSYS完成采样。

3.3 灵敏度分析结果

某车车轴轴段半径参数对最大应力值的灵敏度分析结果见表2。

表2 灵敏度分析结果/mm

由以上灵敏度分析结果各因素的均值可以看出，车轴空心度R0和第3段轴段半径R3对最大应力值的影响较大。空心度R0与最大应力值间成正相关，即空心度R0越大，最大应力值越大，这是因为空心度变大时轴壁变薄，因此车轴所受最大应力值变大。第3段轴段半径R3与最大应力值成负相关，即R3越大，最大应力值越小，这是由于当第3轴段半径变大时（R9=R3，第9轴段半径随第3轴段半径变化），该轴段处轴壁变厚，第3、9轴段中所受应力值变小。因第3、9段轴段处与车轮发生装配，在仿真计算中发现，最大应力值一般出现在第3轴段或第9轴段，因此车轴最大应力值变小。

通过基本因素的标准差值可以考虑交互影响，由以上计算结果各因素的标准差值可以看出，第2轴段半径与其它参数发生的交互影响可以忽略不计。

3.4 结果验证

为验证车轴最大应力值主要受车轴空心度R0和第三轴段半径R3影响，并且与R0呈正相关、与R3呈负相关，笔者设计了四组试验，第一组试验为标准试验，第二组试验在第一组试验的基础上减小了R0的值并且增大了R3的值，第三、四组试验在第二组的试验基础上改变了 R1、R2、R3、R6、R8的值。 四组试验计算结果见表3。

第一组与第二组试验计算结果的对比表明，减小空心度R0并增大第三轴段半径R3可以显著降低车轴最大应力值。对比第二组与第三、四组试验计算结果可见，改变其它几项参数对于最大应力值的影响不大。以上试验对比结果符合灵敏度计算分析得出的结论。

为验证第2轴段半径与其它参数发生的交互影响可以忽略不计，笔者又设计了4组试验，每组试验包含两次计算，每组试验的两次计算令R2取值不等而其它参数取值保持一致，计算两次应力差值。表示其它参数保持在某一水平值时，R2的增量引起的最大应力值的变化。不同试验组间参数R0、R1、R3～R8保持在不同的水平值，而R2增量取值相同，四组试验计算结果见表4。

▲图3 车轴有限元分析模型

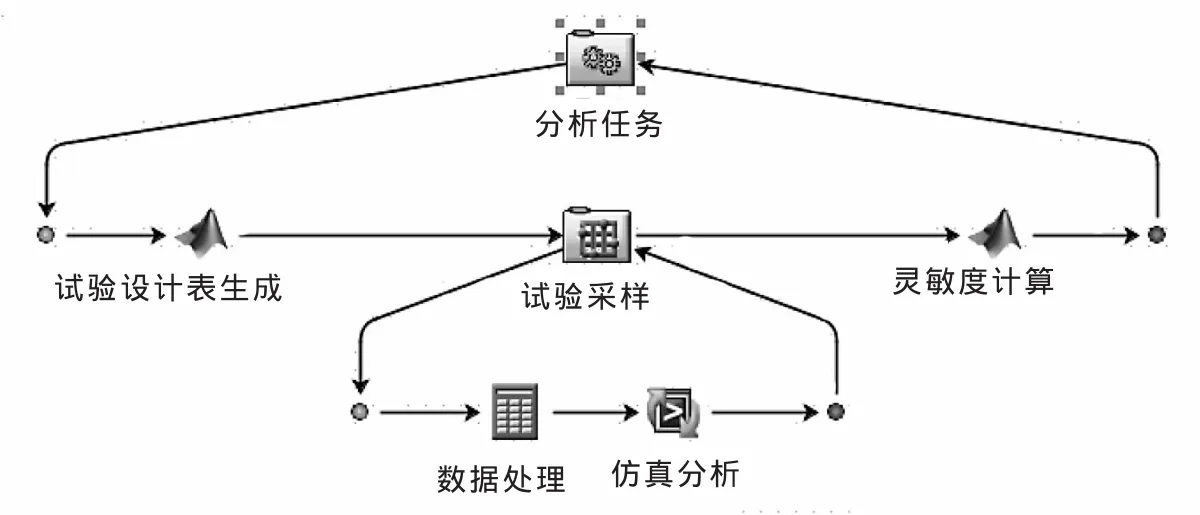
▲图4 Isight流程图

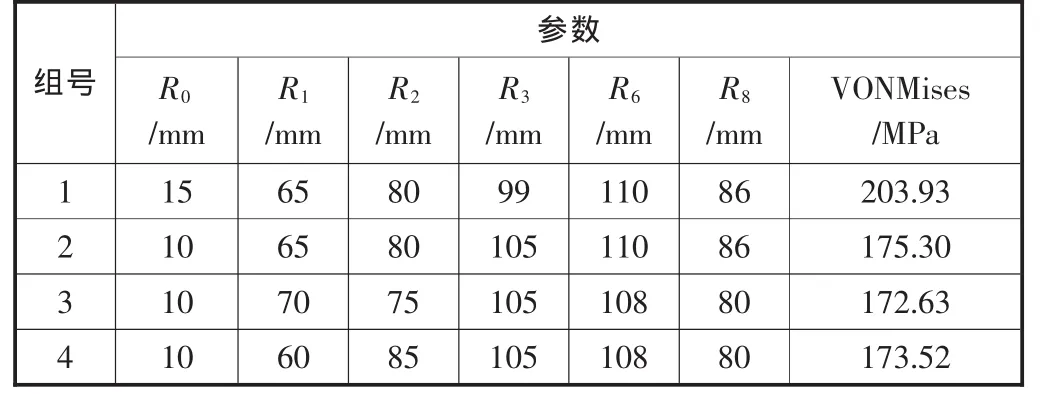
表3 灵敏度验证试验一

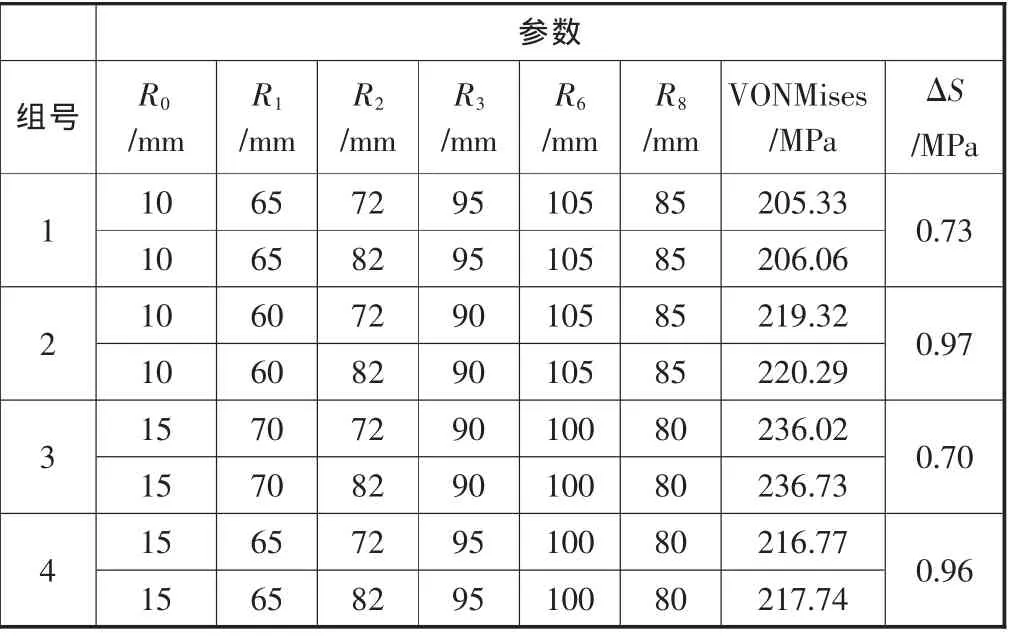
表4 灵敏度验证试验二

由四组试验计算结果可知，在参数R0～R8保持在不同水平值的情况下，R2取同样的增量引起的最大应力值的变化基本一致，R2变化量相同情况下，引起的最大应力值的变化不因其它参数的变化而产生较大差异，由此可见其它参数对于R2的交互影响不明显。

4 结束语

本文在Isight环境下集成了ANSYS车轴有限元分析程序和基于MATLAB自编的Morris灵敏度分析程序，实现了基于Morris方法的车轴结构参数灵敏度分析。以车轴各轴段半径为设计参数进行的灵敏度分析，结果表明，车轴空心度的大小和第3轴段半径大小对车轴最大应力值的影响最大。本文计算结果可为进一步指导车轴结构优化设计提供一定基础依据，同时本文所使用的方法也可运用到对高速列车其它关键零部件的结构参数分析当中。

［1］周素霞.高速列车空心车轴损伤容限理论与方法研究［D］.北京：北京交通大学,2010.

［2］杨大彬,张毅刚,吴金志.基于ANSYS的灵敏度分析及其在单层网壳中的应用［J］.世界地震工程,2009,25（4）:87-91.

［3］尹俊杰,常飞,李曙林,等.基于 Sobol法的整体翼梁损伤容限设计参数灵敏度分析 ［J］.空军工程大学学报,2013,14（6）:9-12.

［4］李彬.网状反射面可展开天线的结构优化设计研究［D］.西安：西安电子科技大学,2010.

［5］Max D.Morris.Factorial Sampling Plans for Preliminary Computational Experiments ［J］.Technometrics,1991,33（2）:161-174.

［6］张艳伟,把多铎,王文川,等.SWMM模型径流参数全局灵敏度分析［J］.农业机械学报,2012,43（7）：42-49.

［7］宋瑾.高速列车车轴的疲劳可靠性灵敏度分析［D］.沈阳:东北大学,2009.

［8］周素霞,谢基龙,宋占勋.影响车轴疲劳强度关键因素的研究［J］.机械制造,2008,46（1）:65-67.

［9］周建斌.机车车轴疲劳问题分析与对策［J］.电力机车与城轨车辆,2008,31（2）:5-7.

［10］袁素粉,袁晓红,陈昌生.基于 ANSYS Workbench的半挂车车轴的强度分析及其优化设计［J］.北京汽车,2011（4）:42-46.