解决交通事故数据分析中零值问题的模型

徐 建，孙 璐

(1.东南大学 交通学院，南京210096;2.美国德克萨斯州大学 奥斯汀分校交通研究中心，奥斯汀78712;3.美国华盛顿Catholic 大学 土木工程系，华盛顿20064)

0 引 言

应用计量模型回归分析交通事故已成为交通安全领域的重要研究内容。由于交通事故具有离散、独立等特性，泊松模型最早被用于研究，后来衍生出大量回归模型。人们在研究回归模型时，主要研究模型中随机项的选取问题以提高拟合效果，却往往忽视对数据集本身的分析。由于交通事故(特别是死亡事故)具有零星、随机、小概率等特征，研究单元(如人口普查区、路段等)在一定时期内往往存在大量零值现象。常规的回归模型如泊松模型、泊松伽马模型或负二项模型等都是假设交通事故发生次数服从伯努利分布，但由于外界因素如环境、地形等，导致某些路段从未发生事故，这与原假设产生矛盾，因此用常规模型来研究大量零值问题，往往无法较好地拟合，甚至会产生错误的结果。

近些年，为了解决这种大量零值问题，研究人员提出了多种回归模型，主要包括3 类，分别是零膨胀模型、多层零膨胀模型和Lindley 模型，每类模型又涉及泊松和负二项两种主要分布。①零膨胀模型。该模型分为两个过程，一个过程假设只产生零值，即观察值的数量为零，另一个过程假设观察值与泊松或负二项分布一致。该模型由Lambert 于1992 年首次提出［1］，并于近些年得到广泛应用，如卡车事故分析［2］、摩托车事故分析［3］、行人事故分析［4］、两车道路段上车辆事故分析［5］、死亡事故分析［6］等。而国内学者较少涉及，其中马壮林等运用零膨胀模型分析了交通事故起数与时间、道路及交通环境等潜在影响因素之间的关系，从时空角度，构建交通事故起数时段、周日和月分布模型［7］。②多层零膨胀模型。多层零膨胀模型主要应用于离散、分层且含有大量零值的数据集。目前该模型多应用于生物医学等领域［8-9］，鲜有用于交通安全领域，特别是交通事故分析。该模型主要包括多层零膨胀泊松和多层零膨胀负二项两种模型，模型拟合过程与零膨胀模型类似，也分为两个过程。③Lindley 模型。该模型由Lindley 于1958 年提出［10］，但直到最近几年才由Zamani 等学者［11-13］应用于交通事故分析。不同于零膨胀模型和多层零膨胀模型的两个拟合过程，Lindley 模型只有一个过程，该过程将Lindley 分布融入到泊松模型或负二项模型。

目前，国内外鲜有文献对这3 类6 种模型的综合分析，研究适用条件和比较拟合效果。基于此，本文首先系统阐述这3 类6 种模型的结构特征、适用条件、参数估计等。其次介绍多种拟合优度措施，包括离差信息准则(DIC)、平均绝对偏差(MAD)、预测均方误差(MSPE)和最大累计残差(MCPD)以及交叉验证评价法(CV)。最后以美国某州2010 年交通事故为实例综合比较和分析。

1 模型设定

为了叙述方便，模型名称以英文字母替代，Poisson 模型为泊松模型;NB 模型为负二项模型;ZIP 模型为零膨胀泊松模型;ZINB 模型为零膨胀负二项模型;MZIP 模型为多层零膨胀泊松模型;MZINB 模型为多层零膨胀负二项模型;Poisson-L模型为泊松Lindley 模型;NB-L 为负二项Lindley模型。

最早应用于交通事故研究的回归模型是Poisson 模型:

式中:Yi为随机变量，表示一定时期内路段i 上发生的交通事故数，i=1，2，3，…，n，即共有n 条路段;yi为Yi的具体观察值;均值与方差相等，即E(Yi)=Var(Yi)=λi。

那么，交通事故数与协变量(即交通事故影响因素)之间的关系如式(2)所示:

式中:β0为截距项，即常数项;βk为第k 个协变量的系数;xik为对应于第i 条路段的第k 个协变量。

近些年研究人员发现交通事故与某个(或某些)协变量存在主要关系，同时由该变量可以构建其他变量，即与其他变量存在一定的相关性，为此提出设置曝光变量。本文采用VMT 即vehiclemiles traveled(车辆路段行驶距离)作为曝光变量。另外，考虑到数据错误、计算误差等，本文引入误差项，如式(3)所示:

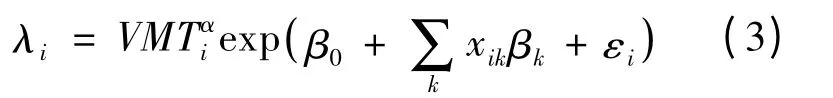
式中:VMTi为曝光变量，表示第i 条路段上车辆行驶总长度;α 为VMTi的系数;εi为误差项，服从伽马分布，即εi～gamma(γ，γ)。

由于Poisson 模型响应变量的均值和方差相等，而实际交通事故的方差往往大于均值，所以该模型有较大的局限性。在Poisson 模型的基础上，NB 模型由于不受这样的约束，得到广泛的应用，如式(4)所示［14］:

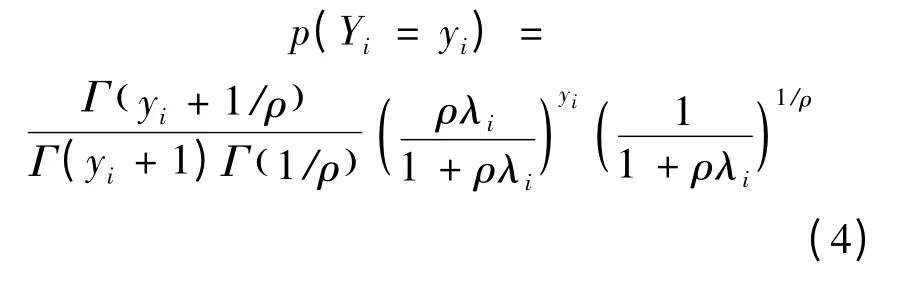
式中:ρ 为过度散布系数，表示变量的散布程度，当ρ=0 时，NB 模型变为Poisson 模型。NB 模型变量的均值E(Yi)=λi，方差Var(Yi)=λi+ρλi2。

1.1 零膨胀模型

零膨胀模型［1］的目的是为了解决计数模型中存在大量零值问题。零膨胀模型分为ZIP 模型和ZINB 模型，模型分为两个过程，一个过程假设只产生零值，另外一个过程假设产生的交通事故数与Poisson 模型或负二项模型一致。本文首先介绍ZIP 模型，如式(5)所示:

式中:yi=0 表示ZIP 模型的第一个过程(称为结构零值)，只产生零值，一般采用对数分布(logit);yi=1，2，…表示第二个过程(称为取样零值)，产生的交通事故数与Poisson 模型一致。

当θi＞0 时，Yi的边缘分布显示过度散布。对应于第一个过程，即结构零值的均值函数为对数线性关系式，如式(6)所示:

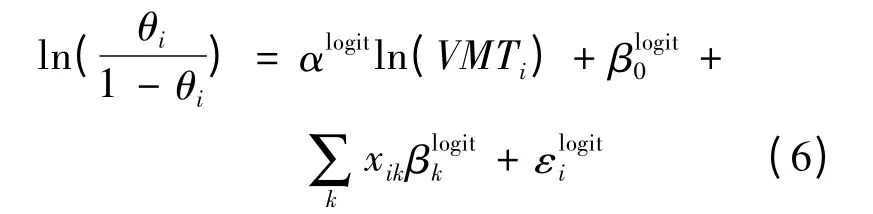
如前面描述，ZIP 模型考虑了过多零值问题，而由于Poisson 分布的局限，未考虑到过度散布问题，而NB 模型则满足过度散布性质，因此将第二个过程由NB 分布代替Poisson 分布，ZIP 模型即变为ZINB 模型，如式(7)所示:

从式(7)可以看出，Poisson 模型、NB 模型、ZIP 模型和ZINB 模型彼此相关，例如，当ρ =0时，ZINB 模型将变为ZIP 模型;当ρ=0 和θi=0时，ZINB 模型将变为Poisson 模型。

以上为ZIP 模型和ZINB 模型的设定过程。针对零膨胀模型的特性，Vuong 在1989 年提出了Vuong 统计检验［15］，用于比较ZIP 模型、ZINB 模型与Poisson 和NB 模型的优劣。Vuong 统计检验可以在统计软件中直接实现，如STATA 软件，或通过编程计算。

1.2 多层零膨胀模型

多层零膨胀模型主要应用于离散、分层且含有大量零值的数据集，目前该模型多应用于生物医学等领域，鲜有用于交通事故分析。该模型主要包括MZIP 模型和MZINB 模型，模型分布过程与零膨胀模型类似，共分为两个过程，一个过程假设只产生零值，另一个过程假设产生的交通事故数与Poisson 模型或NB 模型一致［9］。

首先介绍MZIP 模型。由于ZIP 模型和ZINB模型未考虑分层以及同一层级上的相互关系(非独立性)，因此本文引入两个随机项ηlogiti和ηPi，分别代表logit 过程和Poisson 过程中第i 层级上观察值之间的依赖程度。设Yijk表示在第i 层级第j 个路段上第k 个观察值，其中i=1，2，…，m;j=1，2，…，ni;k=1，2，…，nij。假设不同层级上的观察值相互独立，而同一层级上的观察值存在相互关系，因此表达式为:

式中:wijk和xijk分别为logit 和Poisson 过程协变量;分别是logit 和Poisson 在第j路段第i 层级上的随机误差项:

那么有:

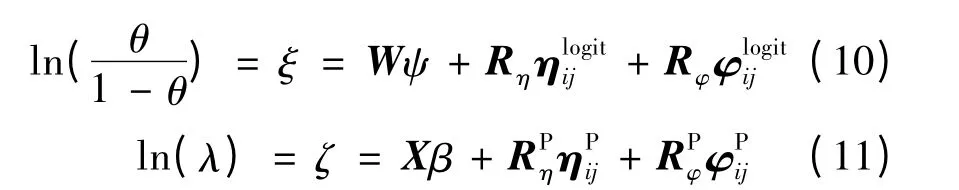
类似于MZIP 模型，MZINB 模型两个过程的均值函数表达式为:

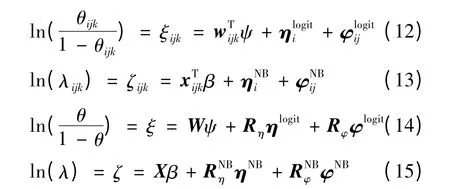
多层零膨胀模型两个过程的参数通过EM 算法估计［9］，即模型的对数似然函数由固定数值EM 算法最大化，进而求得相应的参数估计。

1.3 Lindley 模型

不同于零膨胀模型和多层零膨胀模型的两个拟合过程，Lindley 模型只有一个过程，该过程将Lindley 分布融入到Poisson 模型(Poisson-L 模型)或NB 模型(NB-L 模型)，如式(16)和式(17)所示。这种组合分布具有厚尾性，当数据集含有大量零值时，能较好地拟合［13］。

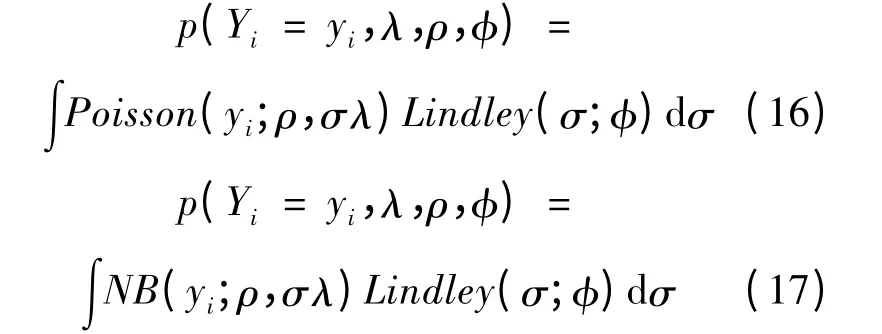
式中:f(λ;ρ，φ)表示f 是变量λ 的分布，ρ 和φ为参数;f 服从Lindley 分布。Lindley 分布是由指数分布和伽马分布组合而成，如式(18)所示:

均值分别为:

假设交通事故数Y 服从Poisson-L 模型或NB-L 模型，那么均值方程为:

可以看出，式(22)与前面描述的式(3)一致。模型的方差为:

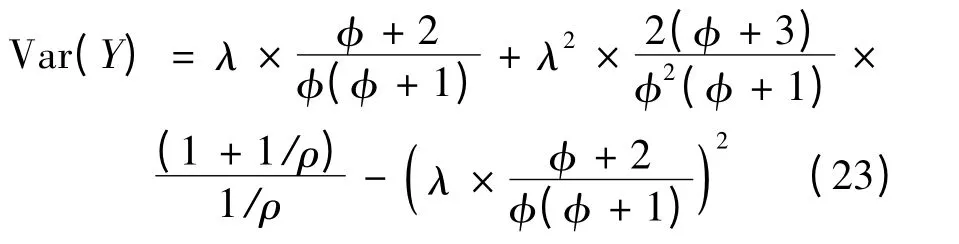
关于Poisson-L 模型和NB-L 模型的参数估计详见文献［11］，通过WinBUGS 软件中用马尔可夫链蒙特卡洛法进行参数估计。

2 模型比较

本文引入多种拟合优度，并采用交叉验证评价法(CV)对模型的拟合效果进行比较。

(1)离差信息准则(DIC)

DIC 基于贝叶斯理论并考虑了模型的复杂性，它与赤池信息准则(AIC)意义相同［15］，表达式为:

(2)平均绝对偏差(MAD)

MAD 是一种模型平均错误预测的测量方法，与平均预测误差(MPB)不同，MAD 的值越接近0时，说明模型预测效果越好［16］，表达式为:

式中:n 为样本量大小。

(3)预测均方误差(MSPE)

MSPE 与均方误差类似，是一种衡量观察事故率与预测事故率差异的方法，同时可以评价数据的变化程度，MSPE 的值越小，说明预测模型具有更好的精确度，表达式为:

式中:n2为样本量大小。

(4)最大累计残差(MCPD)

MCPD 是偏离0 的累计残差(观察事故率与预测事故率的差值)最大绝对值［17］。MCPD 的值越小，说明模型拟合效果越好。

(5)交叉验证评价法(CV)

CV 是一种基于贝叶斯理论，用于评价模型复杂性和拟合情况的方法，它能灵活可靠地检验不同模型的适合度，特别针对大量零值问题。为了减少马尔可夫链蒙特卡洛算法的运算时间，本文引入K-折交叉验证。K-折交叉验证的预测能力表达式可在文献［18］中查询，本文不再赘述。

3 实例分析

3.1 数据概述

本文以美国某州交通事故为实例，选取了该州2010 年发生在州级道路系统内(由州交通厅管理的路网)事故数据集，共计243 388 起。按照同性质要求(同一路段的限速、交通量、路面宽度、车道数、平纵线形等一致)，该州117472.28 km 道路网被划分成277 510 条同性质路段，平均路段长度为0.42 km，其中90%以上的路段长度集中于0 ～1.6 km。

需要说明的是:零膨胀模型和Lindley 模型的研究单元均为同性质路段，而多层零膨胀模型的研究单元分为两个层级:第一层级为人口普查区，第二层级为同性质路段。

利用ArcGIS 软件将243 388 起交通事故与同性质路段合并，即可得到每条路段的交通事故数。将事故数按数量进行划分，如表1 所示。从表中可以看到，82.05%的同性质路段上事故数为零，89.36%的同性质路段未发生受伤事故和死亡事故，因而，该数据集存在大量零值现象。

表1 路段上交通事故数分布Table 1 Distributions of crash counts on segments

3.2 因素选取

本文中响应变量为交通事故数，曝光变量为车辆路段行驶距离VMT(VMT=AADT×路段长度×365)，而其他协变量主要包括几何线形、交通特性和天气状况3 类共8 种，这些协变量的均值、标准差、最小值和最大值如表2 所示。这里需要说明的是，平均路肩宽度指外侧路肩和内侧路肩的平均值;中央分隔带宽度不包含内侧路肩宽度;平曲线度数指每一百英尺对应的曲线度数。

表2 路段的变量统计结果Table 2 Summary statistics of variables for segments

3.3 结果分析

本文运用基于贝叶斯理论的马尔可夫链蒙特卡洛算法估计模型参数［19］，推演过程共有6 条马尔可夫链，每条链迭代20 000 次，前5000 次迭代作为burn-in 过程，以消除初始参数的影响，余下15 000 次迭代用于参数估计;同时，本文采用Gelman-Rubin(G-R)收敛统计来验证收敛适用性，G-R 收敛统计值小于1.1。整个模型估计在WinBUGS 软件中完成，最终回归结果如表3 所示。注:ZIP 模型、ZINB 模型、MZIP 模型和MZINB 模型的logit 过程，即结构零值过程的系数和标准差未显示在表格中。

从表3 可知:6 种模型的协变量系数与标准差各不相同，特别是有些协变量的边际效应在不同模型中甚至出现完全相反的结果，如车道数和降雨量对交通事故的影响，在ZIP 模型和MZIP 模型中成负相关，而在其他4 种模型中则成正相关;另外，车道年平均日交通量在ZIP 模型、ZINB 模型、MZIP 模型和Poisson-L 模型中与交通事故成负相关，而在MZINB 和NB-L 模型中成正相关。这充分说明不同模型会有不同的参数估计，产生不同的拟合效果。

从表3 同样可以得到:曝光变量(VMT)和车道数、车道年平均日交通量以及降雨量等协变量与交通事故数成正相关，即交通事故数随着协变量数值增大而增加，而其他协变量成负相关。值得注意的是，从直觉来讲最大限速越高，事故越多，但统计结果却完全相反，即并非限速越高事故越多，可能由于限速高的路段线形往往更好，同时驾驶员注意力更集中，事故反而少。表4 为各模型拟合优度比较结果。

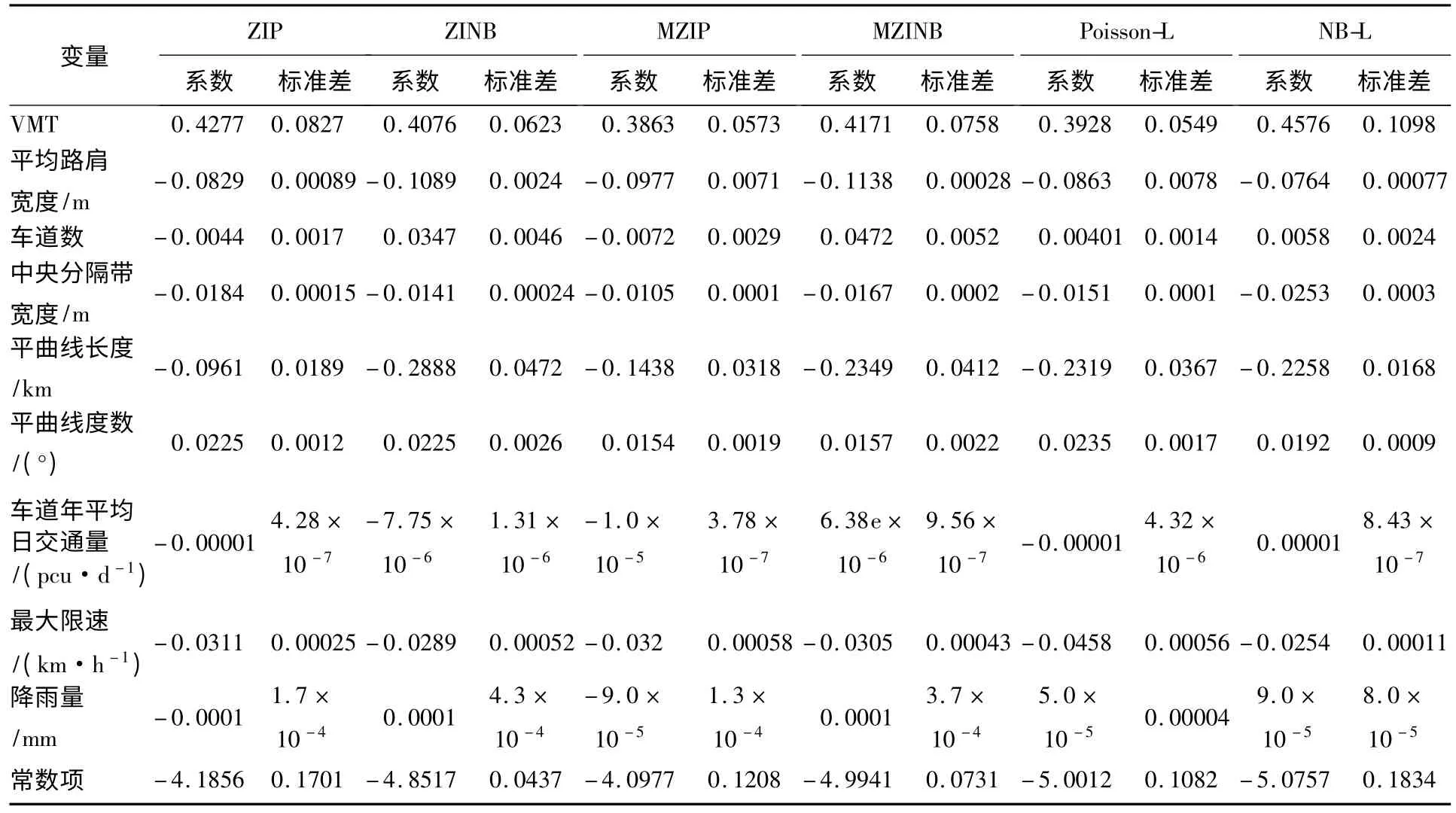
表3 各交通事故模型的估计结果Table 3 Estimation results of models for crash count

从表4 中可以看出:NB-L 模型的离差信息准则(DIC)最小，其他依次是MZINB 模型、ZINB 模型、Poisson-L 模型、MZIP 模型，最大是ZIP 模型。由于DIC 越小说明模型拟合效果越好，由此得到，NB-L 模型的拟合效果最好，其次是MZINB 模型。类似于离差信息准则(DIC)，通过比较平均绝对偏差(MAD)、预测误差均方(MSPE)和最大累计残差(MCPD)，均可得到相同的结论。需要说明的是，本文采用的数据集具有较强的过度散布性(从表2 可以看出，交通事故数的方差远大于均值)，因而NB 模型比Poisson 模型更合适。若将NB 模型和Poisson 模型分开比较，可知Lindley 模型比多层零膨胀模型和零膨胀模型更合适，而多层零膨胀模型又比零膨胀模型更合适。

表4 各交通事故模型拟合优度比较Table 4 Comparison of goodness-of-fit of models for crashes

除了比较4 种拟合优度(DIC、MAD、MSPE 和MCPD)外，本文还选取了交叉验证评价法(CV)，图1 表示各模型的CV 预测能力，注:由于路段最大事故数达到387 起(见表2)，图1 仅显示同性质路段上事故数为0 ～10 起，超过10 个事故数的未显示。从图中可以看出，虽然针对不同事故数，各模型的预测能力不尽相同，但总体上NB-L 模型的预测能力最强，MZINB 模型次之，而ZIP 模型预测能力最弱，这与前面4 种拟合优度的比较结果类似。

4 结束语

针对交通事故数据分析中大量零值问题，本文对目前已有的3 类6 种模型综合分析，发现ZIP 模型、ZINB 模型、MZIP 模型和MZINB 模型分为两个过程(结构零值和取样零值)，其中MZIP 模型和MZINB 模型适合于分层数据集，而Poisson-L 模型和NB-L 模型只有一个过程，这更符合统计学理论;同时，通过离差信息准则(DIC)、平均绝对偏差(MAD)、预测误差均方(MSPE)和最大累计残差(MCPD)等4 种拟合优度以及交叉验证评价法(CV)，以美国某州2010 年交通事故为实例，运用马尔可夫链蒙特卡洛算法，结果表明，3 类模型中Lindley 模型拟合效果最好，多层零膨胀模型其次，而6 种模型中负二项Lindley 模型拟合效果最好，MZINB 模型其次。本文可为运用计数模型研究大量零值现象提供借鉴和参考。

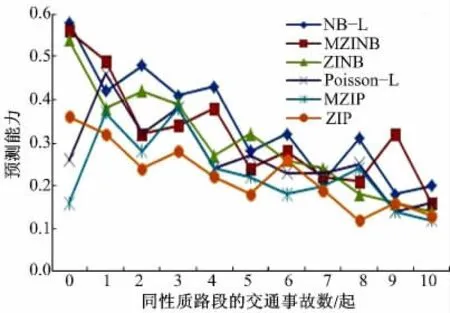
图1 各模型的CV 预测能力比较Fig.1 Model comparison of predictive abilities using cross-validation

［1］Lambert D.Zero-inflated poisson regression，with an application to defects in manufacturing［J］.Technometrics，1992，34(1):1-14.

［2］Miaou，S.The relationship between truck accidents and geometric design of road sections:poisson versus negative binomial regressions［J］.Accident Analysis＆Prevention，1994，26(4):471-482.

［3］Lee J，Mannering F L.Impact of roadside features on the frequency and severity of run-off-road accidents:an empirical analysis［J］.Accident Analysis＆Prevention，2002，34(2):349-361.

［4］Shankar V N，Ulfarsson G F，Pendyala R M，et al.Modeling crashes involving pedestrians and motorized traffic［J］.Safety Science，2003，41(7):627-640.

［5］Qin X，Ivan J N，Ravishankar N.Selecting exposure measures in crash rate prediction for two-lane highway segments［J］.Accident Analysis＆Prevention，2004，36(2):183-191.

［6］Yan Xue-dong，Wang Bin，An Mei-wu，et al.Distinguishing between rural and urban road segment traffic safety based on zero-inflated negative binomial regression models［DB/OL］.［2013-01-18］.http://www.hindawi.com/journals/ddns/2012/789140/.

［7］马壮林，邵春福，胡大伟，等.高速公路交通事故起数时空分析模型［J］.交通运输工程学报，2012，12(2):93-99.Ma Zhuang-lin，Shao Chun-fu，Hu Da-wei，et al.Temporal-spatial analysis model of traffic accident frequency on expressway［J］.Journal of Traffic and Transportation Engineering，2012，12(2):93-99.

［8］Lee A H，Wang Kui，Scott J A，et al.Multi-level zeroinflated Poisson regression modeling of correlated count data with excess zeros［J］.Statistical Methods in Medical Research，2006，15(1):47-61.

［9］Moghimbeigi A，Eshraghian M R，Mohammad K，et al.Multilevel zero-inflated negative binomial regression modeling for over-dispersed count data with extra zeros［J］.Journal of Applied Statistics，2008，35(10):1193-1202.

［10］Lindley D V.Fiducial distributions and Bayes＇theorem［J］.Journal of the Royal Statistical Society，1958，20(1):102-107.

［11］Zamani H，Ismail N.Negative binomial-Lindley distribution and its application［J］.Journal of Mathematics and Statistics，2010，6(1):4-9.

［12］Lord D，Geedipally S R.The negative binomial-Lindley distribution as a tool for analyzing crash data characterized by a large amount of zeros［J］.Accident Analysis and Prevention，2011，43(5):1738-1742.

［13］Reddy G S，Lord D，Dhavala S S.The negative binomial-Lindley generalized linear model:Characteristics and application using crash data［J］.Accident Analysis＆Prevention，2012，45(3):258-265.

［14］Miaou S.The relationship between truck accidents and geometric design of road sections:Poisson versus negative binomial regressions［J］.Accident Analysis＆Prevention，1994，26(4):471-482.

［15］Vuong Q H.Likelihood ratio tests for model selection and non-nested hypothesis［J］.Econometrica，1989，57(2)，307-333.

［16］Oh J，Lyon C，Washington S P，et al.Validation of the FHWA crash models for rural intersections:lessons learned［C］∥Transportation Research Record，Transportation Research Board，National Research Council，Washington DC，2003:41-49.

［17］Geedipally S R，Patil S，Lord D.Examination of methods for estimating crash counts according to their collision type［J］.Transportation Research Record，Transportation Research Board，National Research Council，Washington DC，2010:12-20.

［18］Huang H L，Chin H C.Modeling road traffic crashes with zero-inflation and site-specific random effects［J］.Statistical Methods＆Applications，2010，19(3):445-462.

［19］Thomas A，O＇Hara B，Ligges U，et al.Making BUGS open［J］.R News，2006，6(1):12-17.