斜采样的倾斜角度对采样产生混叠的影响及其与分辨率的关系

王京萌，张爱武，赵宁宁，孟宪刚

(1.首都师范大学 资源环境与旅游学院，北京100048;2.三维信息获取与应用教育部重点实验室，北京100048;3.资源环境与地理信息系统北京市重点实验室，北京100048;4.城市环境过程与数字模拟国家重点实验室培育基地，北京100048)

0 引 言

遥感技术的发展使高质量遥感图像的应用成为现实，国外先进的遥感图像分辨率越来越高。通过改进硬件设备提高分辨率会增加成本或者受到技术的限制。鉴于此，通过改变采样模式提高图像分辨率的方法得到更多关注。将斜模式采样(简称斜采样)、高模式采样和超模式采样结合进行图像后期处理，可以有效地提高图像分辨率。斜采样为单线阵，避开了两排错位排列探测器的难题，更具有实践性。通过使线阵CCD 与推扫方向成一定的夹角来增大采样密度的方式提高分辨率，同时也会产生混叠。按照Nyquist 采样定理，当采样频率小于截止频率2 倍时，图像将产生混叠;当采样网格由于微小抖动产生的欠采样也会产生混叠;A/D 转换或星地数据传输的压缩或解压缩过程中也可能产生混叠;在后期处理图像的抽取或插值操作等都可能产生混叠现象。

国外学者［1］将混叠分为带外和带内虚假响应。文献［2］专门针对SPOT－5 成像系统，研究了混迭现象和去除混迭的方法，并应用到遥感图像复原的模型当中。孟庆武［3］根据星载CCD 设备的成像机理，定义了卫星图像的混叠度，在超分辨率处理模型中联合估计混叠度、运动参数和高分辨率图像。范冲等［4］通过去除低分辨率影像中由于欠采样产生的频率中心的部分低频进行图像配准。张智等［5］将倒易晶胞与小波结合进行复原，同样也考虑了混叠的因素。在斜采样的混叠去除方面，郑钰辉等［6］分析了斜采样条件下混叠现象的产生机理，用最佳倒易晶胞理论求出受混叠和噪声影响最小的频谱来提高分辨率。高陆云等［7］利用斜模式自适应倒易晶胞的非局部正则化模型来进行图像超分辨率重建。对于斜采样的倾斜角度，周峰［8］在试验的基础上提出，探测器阵列旋转45°并且推扫方向采样间距减半，相对常规线阵推扫采样，图像的空间分辨率可以提高1.64 倍左右。但是并没有明确斜采样的不同倾斜角度对混叠的影响;没有比较常规采样与斜采样的混叠程度大小;也没有说明分辨率提升与混叠之间的关系。

本文从采样理论出发，分析了斜采样的采样网格，进而明确了混叠过程，根据倒易晶胞的理论和香农采样定理，把图像由空域中转换到频域中，计算符合分辨率最高特定混叠阈值的倒易晶胞约束，通过倒易晶胞的面积与混叠程度的关系推出衡量混叠程度的指标——混叠指数。计算倾斜角度为1°～89°的混叠指数，得到混叠随角度变化的规律。引入空间有效分辨率，研究了倾斜角度与空间有效分辨率的关系。深入研究了斜采样的同一倾斜角度的空间有效分辨率与混叠的关系;利用最小二乘曲线拟合了混叠与空间有效分辨率的关系曲线。明确了倾斜角度与混叠及分辨率之间的关系，从而指导实际应用以满足特定混叠和分辨率的需求。

1 图像采集系统模型及六边形采样网格

1.1 图像采集系统模型

通常情况下，一般的采样系统由两部分组成:一部分是在焦平面对入射光线对焦的光学系统;另一部分是在一定时间内，分布在焦平面的传感元件计算满足确定位置的光子数。整个系统在采集时可能是移动的，因此图像采样系统模型可表示成如下形式:

式中:H 为设备的传递函数，它由多个因素决定;ΔΓ表示基于传感器阵列几何形状的采样单元，Γ为传感器的几何形状;g 为采集到的图像;f 为原始理想图像;n 为噪声。

H 可以看成一个低通滤波器。大体可以看作三部分效应的乘积:

式中:Hsen为传感器在其敏感区域(如正方形)获得的光子数:

式中:c 为探元尺寸;β 为系统参数。

Hmov(ξ，η)为传感器在移动过程中采集的图像:

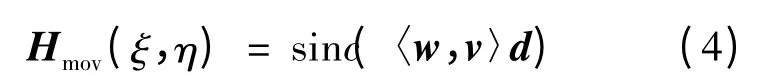
式中:w=(ξ，η)，v=(cosθ，sinθ)为向量，θ 为斜采样的倾斜角度，rad;d 为每一帧运动的距离。

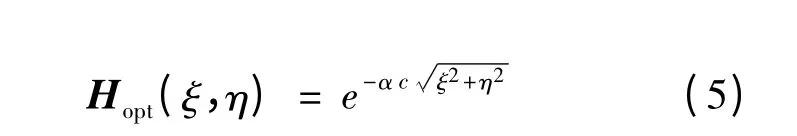
式中:α 为系统参数。

理想系统中α=0，β=0，较理想的系统α=1.9，β=0.9;常规系统α=0.3，β=0.14。本文使用常规系统的两个参数，将式(3)～(5)代入式(2)绘制出图像和采样网格如图1 所示(斜采样以60°倾斜角为例)。

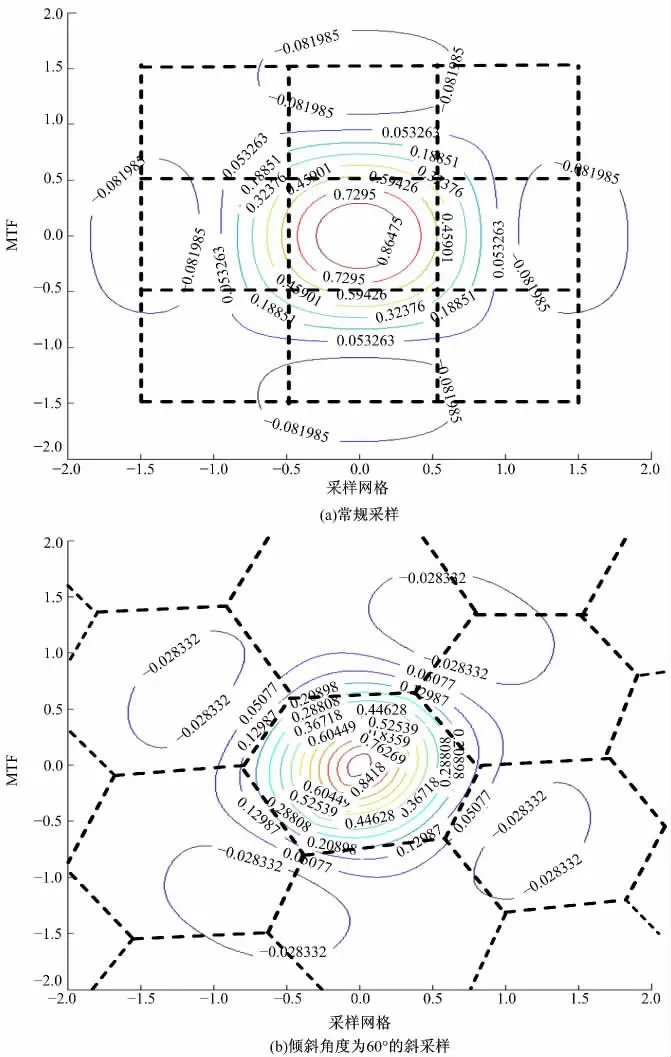
图1 常规采样和倾斜角度为60°的斜采样的系统调制传递函数和采样网格Fig.1 MTF and sampling grids of regular sampling and the MTF and sampling grids of tilting angle 60°

1.2 六边形采样网格及混叠的本质

本文从采样的角度分析混叠的成因，对斜采样的采样网格进行分析。斜采样模式如图2 所示。θ 为线阵相机推扫的方向与线阵的夹角(后文提到的倾斜角度指的均为该角度)。一般认为离散图像是规则的采样网格:

式中:{e1，e2}是ℝ2的基。每个采样网格对应的傅立叶域的对偶网格为:

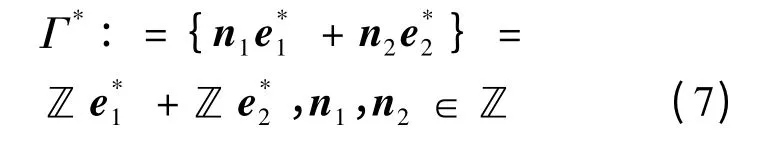
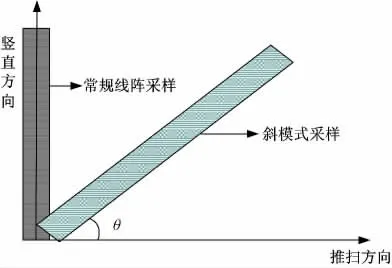
图2 斜采样模式示意图Fig.2 Sketch map of tilting mode sampling

由于斜采样可能产生四边形或六边形的网格，四边形和六边形也是最常见的采样网格:

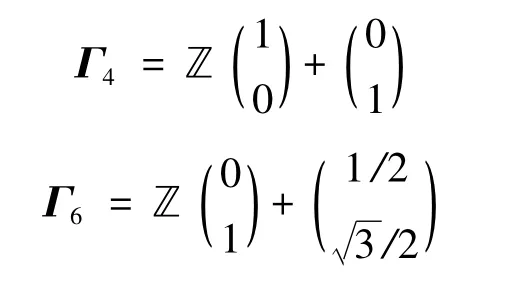
相应的对偶网格为:

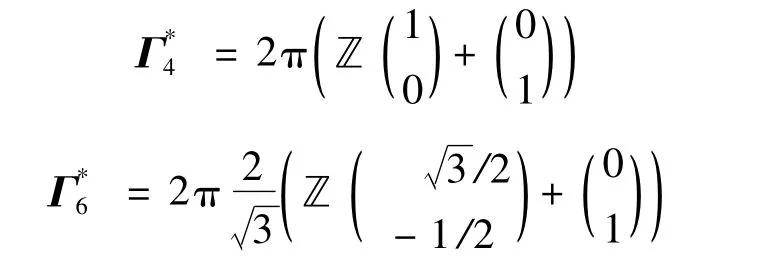
传感器阵列由一些形状和性质相同、中心位于规则的网格中的探元组成。这些网格无重叠地覆盖了整个图像平面，将这个覆盖称泰森晶胞单元。需要说明的是:采样间距p 的不同产生的采样网格的几何形状也不同。为了对比相同条件下角度对混叠的影响，在实际的斜采样系统中，令采样间距与常规采样相同，都等于探元尺寸的大小c，即p=c。斜采样的采样模式和采样网格中的泰森晶胞单元如图3 所示，其中以θ=30°为例。

绘制出斜采样的采样网格情况，相应频域的频谱复制情况就明确了，混叠的本质就是频谱在周期延拓中谱带的叠加，可以表示为［9］:

式中:F 为带有混叠的图像频谱;G 为真实的图像频谱;Galias为混叠频谱;N 为噪声的频谱。式(8)即为带有混叠的图像的组成。

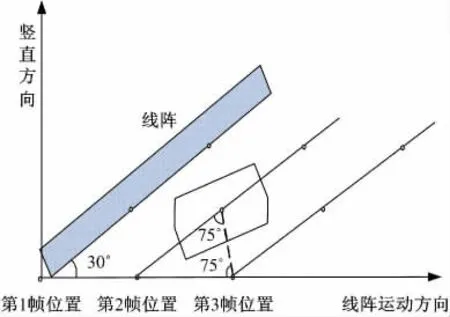
图3 倾斜角度为30°的斜采样模式及其泰森晶胞单元Fig.3 θ=30°tilting mode sampling and its voronoi cell

2 混叠的衡量及分辨率的计算

2.1 混叠指数AI

混叠度的计算参考最佳倒易晶胞中的混叠相关项，计算满足混叠系数阈值的最佳倒易晶胞，倒易晶胞的面积与原始图像的面积比值的大小反应了混叠程度的大小。混叠相关项为:

式(9)表示图像不同像素位置混叠的程度。

本文假设图像是属于BV 空间［10－13］，因为Ω上的有界变分函数空间定义为:

式中:u=u(x，y);TV(u)=∫Ω|∇u|dxdy;∇u=(ux，uy);Ω∈ℝ2。BV 空间是一种确定性图像模型，允许跳跃或边的存在，适用于非纹理图像，能够较好地保持图像的边缘信息［14－15］。Almansa 假设，获得了傅立叶衰减系数大致服从，其中p=1.6，并经过大量的图像实验组证明此假设是正确的［2］。这样根据式(9)便可求得最小混叠范围为:

将AI 作为衡量混叠程度的指标(AI 为混叠指数);DHF为原图像矩阵的面积积分。AI 是根据混叠相关项得出的，因此AI 能说明混叠程度的大小，可以作为衡量混叠程度的指标之一。AI 越大证明混叠越大。

2.2 空间有效分辨率

遥感图像的分辨率一般通过GSD 和名义分辨率［16］计算，但是这两种算法没有突出混叠程度在分辨率中的作用，因此，本文引入考虑混叠和噪声影响的空间有效分辨率。既需考虑噪声的影响，又考虑混叠的影响才能称为考虑混叠的分辨率，将噪声和混叠分别设定一定的权重参与影响分辨率。

由式(8)可知，混叠是由真实图像、混叠频谱、噪声频谱的叠加形成的。则将混叠和噪声作为一定的权重加入空间分辨率形成有效分辨率的形式如下:

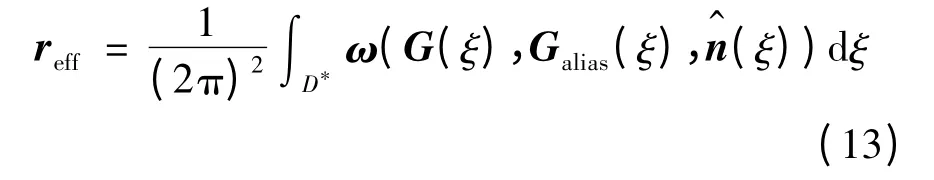
式中:权重函数可以变换为:

必须对W 做一个限定，以便对高水平的混叠和噪声作出惩罚:

式中:W(·，b)、W(a，·)分别相对于b、a 为非增函数。

基于以上特性，构造权重函数为:

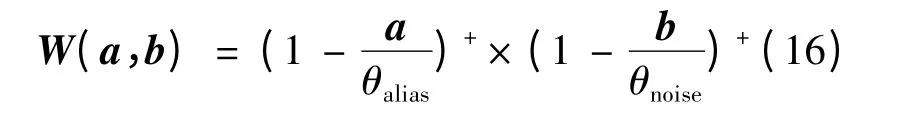
式中:(s)+=max(0，s)也就是取非负值，θalias、θnoise分别为相对混叠、相对噪声的阈值。当a ≥θalias或b ≥θnoise时，相对混叠系数或相对噪声系数超出规定的阈值，1－a/θalias＜0 或1－b/θnoise＜0，则W(a，b)=0(式(15))。原则上应该设定θalias≈θnoise≈1 来表示当混叠或噪声大于真实信号的情况，此时傅立叶系数基本不含有用信息。但是，由于人类的感知系统能够容忍噪声的水平远高于混叠水平，应设定θalias=θnoise。本文试验中设定θalias=0.2，θnoise=5［2］。

a 可以根据式(9)求出，b 的值可根据式(17)求得:

式中:N2为频域噪声的方差，由于f 为未知量;n噪声未知，则式(13)可以表示为:

进一步将式(18)化简［2］:

由于空间分辨率一般被定义为每英尺的点数(dpi)，或每英尺的采样行数(lpi)，是采样密度的度量。有效分辨率(式(13))为带权重的空间分辨率(空间分辨率权重为1)，也就是表示单位面积的点数［17］，将它开根号就表示每行(列)的点数，这样谱的微小差异就能反映出来。再对其取倒数，表示相邻采样点的距离所占的比例，用该比例来表示空间有效分辨率。那么，空间有效分辨率即为有效分辨率的－1/2 次方:

本文以式(20)作为衡量有混叠情况下图像的空间有效分辨率。空间有效分辨率的值越大，分辨率越低。

3 倾斜角度对混叠程度的影响分析

对于斜采样的不同倾斜角度，考虑混叠的影响，使用本文定义的混叠指数AI 进行衡量，在求AI 之前，要对仅考虑混叠的［18］最佳倒易晶胞进行求解。

图4 为常规采样和倾斜角度为60°时，满足混叠系数阈值的最佳倒易晶胞示意图(白色部分为倒易晶胞面积)。为了研究倾斜角度对混叠的影响，必须在其他条件都一致的情况下才能比较，因此，使图像大小均为401×401，采样间距均为c=1，采用相同的成像系统，假设采样外界条件亦相同。经过计算，常规采样(倾斜角度为90°)的最佳倒易晶胞为∫D*1=23 364，对每隔1°的倾斜角度的倒易晶胞进行计算，1°～89°最佳倒易晶胞的面积(a ＜0.2)如图5 所示，每幅的大小为401×401 像素。求出倒易晶胞面积是为了求混叠指数AI 做准备，经过计算并绘制了混叠指数AI 与倾斜角度的关系，如图6 所示。

图4 常规采样和倾斜角度为60°的最佳倒易晶胞Fig.4 Optimal reciprocal cell of regular sampling and tilting mode 60°

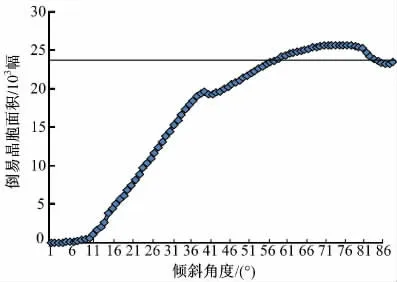
图5 最佳倒易晶胞面积曲线图Fig.5 Graph of optimal reciprocal cell area

图6 混叠指数图Fig.6 Aliasing index graph

分析图5 的面积曲线可知:随着倾斜角度的增大，斜采样的最佳倒易晶胞面积整体呈上升趋势，在倾斜角度为40°和85°附近呈下降趋势，并略微波动。晶胞面积的最大值位于倾斜角度为78°处，图中横线表示常规采样的最佳倒易晶胞面积，将常规采样最佳倒易晶胞面积与斜采样倒易晶胞面积置于同一坐标系下，可以看出比常规采样晶胞面积大的倾斜角度为58°～87°。对于倾斜角度与最佳倒易晶胞面积的曲线不能直接看出混叠与倾斜角度的关系，由于相同大小图像的倒易晶胞面积越大，说明满足容忍限度的混叠面积越大;又因为在频域中，高频部分分布在外围，这样面积越大说明图像细节的保持能力越好，混叠的程度就越小。因此绘制混叠指数AI 与倾斜角度的关系(见图6)，可以直接反映混叠与倾斜角度的关系:随着斜采样倾斜角度的增大，混叠程度整体呈减小趋势(在倾斜角度为41°和82°附近略有上升趋势波动)，混叠最小值也在倾斜角度为78°处。经过计算，常规采样的混叠指数为0.8574(图6 中横线所示)，因此，斜采样的混叠程度比常规采样小的倾斜角度范围为57°～89°。也就是说在采样间距为p=c，其他条件都相同的情况下，常规采样要比倾斜角度为1°～56°的混叠程度小。随着倾斜角度的变化，系统的调制传递函数(MTF)也发生变化，控制采样间距不变可以看出倾斜角度对混叠的影响。从混叠指标与倾斜角度关系的分析可以看出，倾斜角度为57°～89°，倾斜角度对系统MTF 的变化产生的混叠影响较常规采样小。在设计倾斜角度时，可以参考此范围，并改变采样间距来达到超分辨率的目的。

4 空间有效分辨率与混叠关系分析

斜采样成像的最终目的还是为了提高图像的分辨率。衡量遥感图像的分辨率的方法主要是地面采样间距(GSD)［19］，它仅与卫星的轨道高度和相机的光学焦距有关系，没有考虑成像质量及采集模式改变的影响，空间有效分辨率能考虑噪声及混叠的影响，更精确地计算斜采样的分辨率。

4.1 倾斜角度与空间有效分辨率的关系

噪声模型不会引起严重问题，通常选择高斯白噪声分布N(0，σ)就足够精确，本文在计算时加入了均值为0，方差为0.01 的高斯噪声。为了便于对比，将空间有效分辨率归一化表示。图7为斜采样倾斜角度为1°～89°的空间有效分辨率。

图7 空间有效分辨率随倾斜角度变化曲线Fig.7 Curve of spatial effective resolution when tilting angle various

图7 中，空间有效分辨率的值随着倾斜角度的增大逐渐减小。验证了理论上的“倾斜角度增大，采样密度增大，分辨率就随之增大”的原理。空间有效分辨率最高出现在倾斜角度为75°处。混叠最小角度和分辨率最高角度未出现在同一角度，可能是因为噪声和混叠共同作用于分辨率使混叠最小角度与空间有效分辨率最高角度略有差异，但是角度相差3°可以认为二者基本一致。经过计算得出，比常规采样的分辨率高的倾斜角度为58°～87°。此范围也与混叠指数有小于±2°的偏差，范围基本一致。混叠最小角度与分辨率最高角度在一定程度上为同一角度，这样又能说明混叠与分辨率之间是有一定的关系的，它们的关系在4.2 节中进行分析。

4.2 图像混叠与分辨率的关系

将倾斜角度固定，把混叠指数AI 值与空间有效分辨率值置于同一坐标系下，并进行曲线拟合，可以得出相同倾斜角度的混叠程度与分辨率之间的关系，如图8 所示。

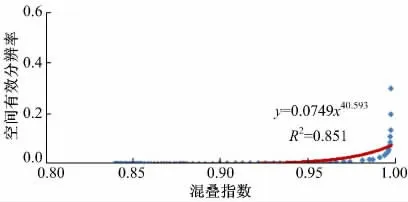
图8 混叠指数与空间有效分辨率的关系曲线Fig.8 Relationship curve between aliasing index and spatial effective resolution

使用最小二乘法对相同倾斜角度的混叠指数AI 与空间有效分辨率绘制的离散点进行曲线拟合，得到空间有效分辨率随混叠程度增大的关系为幂指数关系，关系表达式为:y=0.0749x40.593，相关系数为0.851，可以说明这两者之间是高度相关的，即随着混叠程度的增大，有效分辨率是逐渐增大的，空间有效分辨率是逐渐降低的。这与常规理解的“混叠对分辨率起到降低的影响”相统一。在实际的斜采样试验设计中，可以选择混叠最小的角度与分辨率最高的角度基本一致的75°～78°，能够达到混叠最小和分辨率最高的统一，可以减小去混叠造成的误差，又能使分辨率达到最高。

5 结 论

(1)斜采样的混叠程度随着倾斜角度的增大而减小;使混叠程度比常规采样小的倾斜角度为57°～89°;使混叠最小的倾斜角度为78°。

(2)空间有效分辨率随着倾斜角度的增大而增大。符合“倾斜角度增大，采样密度增大，分辨率就随之增大”的原理。分辨率最高出现在倾斜角度为75°时，比常规采样的分辨率高的倾斜角度为58°～87°。

(3)经过最小二乘曲线拟合，得出混叠程度与分辨率之间是幂指数关系，关系式为:y =0.0749x40.593。随着混叠程度的增大，空间有效分辨率逐渐降低，这与常规理解的“混叠对分辨率是起到降低的作用”相一致。

［1］Chen Z，Karim M A，Hayat M M.Elimination of higher order aliasings by multiple interlaced sampling［J］.Optical Engineering，1999，38(5):879－885.

［2］Almansa A，Durand S，Rougé B.Measuring and improving image resolution by adaptation of the reciprocal cell［J］.Journal of Mathematical Imaging and vision，2004，21(3):235－279.

［3］孟庆武，孟新.联合估计混叠度，运动参数和高分辨率图像的JEMAP 算法［J］.计算机科学，2004，31(6):184－188.Meng Qing－wu，Meng Xin.Joint estimation MAP algorithm of aliasing degree，registration parameters and high－resolution image［J］.Computer Science，2004，31(6):184－188.

［4］范冲，龚健雅，朱建军.一种基于去混叠影像配准方法的POCS 超分辨率序列图像重建［J］.测绘学报，2006，35(11):358－363.Fan Chong，Gong Jian－ya，Zhu Jian－jun.POCS superresolution sequence image reconstruction based on image registration excluded aliased frequency domain［J］.Acta Geodaetica et Cartographica Sinica，2006，35(11):358－363.

［5］张智.面向遥感图像的倒易晶胞复原方法研究［D］.南京:南京理工大学计算机科学与技术学院，2008.Zhang Zhi.Research on reciprocal cell restoration oriented to remote sensing image［D］.Nanjing:School of Computer Science and Technology，Nanjing University of Science＆Technology，2008.

［6］郑钰辉，汤杨，陈强，等.提高斜模式遥感图像有效分辨率的方法［J］.计算机辅助设计与图形学学报，2009，21(2):243－249.Zheng Yu－hui，Tang Yang，Chen Qiang，et al.A method for increasing effective resolution of tilting mode satellite image［J］.Journal of Computer－aided Design＆Computer Graphics，2009，21(2):243－249.

［7］高陆云.基于倒易晶胞的遥感图像恢复技术研究［D］.南京:南京理工大学计算机科学与技术学院，2009.Gao Lu－yun.Technology of restoration of remote sensing image based on reciprocal cell［D］.Nanjing:School of Computer Science and Technology，Nanjing University of Science＆Technology，2009.

［8］周峰，王怀义，马文坡，等.提高线阵采样式光学遥感器图像空间分辨率的新方法研究［J］.宇航学报，2006，27(2):227－232.Zhou Feng，Wang Huai－yi，Ma Wen－po，et al.A study on a new method for improving image spatial resolution of sampled optical imager with single array［J］.Journal of Astronautics，2006，27(2):227－232.

［9］周峰.提高采样式光学遥感器图像空间分辨率的方法研究［D］.北京:中国空间技术研究院，2005.Zhou Feng.A method of improving the resolution of optical remote sensor image［D］.Beijing:China Academy of Space Technology，2005.

［10］Ambrosio L.A compactness theorem for a special class of functions of bounded variation［J］.Boll Un Mat Ital，1988，3－B(7):857－881.

［11］Ambrosio L，Fusco N，Pallara D.Functions of Bounded Variation and Free Discontinuity Problems［M］.New York:Oxford University Press，2000.

［12］Evans L C，Gariepy R F.Measure Theory and Fine Properties of Functions［M］.Boca Raton:CRC Press，1992.

［13］Giusti E.Minimal Surfaces and Functions of Bounded Variation［M］.Boston:Birkhäuser，1984.

［14］Rudin L I，Osher S，Fatemi E.Nonlinear total variation based noise removal algorithms［J］.Physica D:Nonlinear Phenomena，1992，60(1):259－268.

［15］罗群利.四阶向量值图像去噪问题的快速算法［D］.长沙:湖南大学数学与计量经济学院，2012.Luo Qun li.A fast algorithm for forth－order vector－valuedimage denoising［D］.Changsha:College of Mathematics and Econometrics，Hunan University，2012.

［16］郑钰辉.空域自适应滤波方法及其在斜模式遥感图像复原中的应用［D］.南京:南京理工大学计算机科学与技术学院，2009.Zheng Yu hui.Spatial adaptive filter methods and theirs applications in the tilting mode satellite image restoration［D］.Nanjing:School of Computer Science and Technology，Nanjing University of Seience and Technolog，2009.

［17］王静，徐丽燕，夏德深.斜采样技术的混叠分析及分辨率计算［J］.电子学报，2012，40(5):1067－1072.Wang Jing，Xu Li－yan，Xia De－shen.The aliasing analysis and resolution calculation of tilting sampling system［J］.Acta Electronica Sinica，2012，40(5):1067－1072.

［18］周峰，乌崇德.提高航天传输型CCD 相机地面像元分辨率方法研究［J］.航天返回与遥感，2002，23(3):35－42.Zhou Feng，Wu Chong－de.A method for improving GSD of Space Real－time transmission CCD Camera［J］.Spacecraft Recovery＆Remote Sensing，2002，23(3):35－42.

［19］王静.基于成像系统建模提高遥感图像分辨率方法研究［D］.南京:南京理工大学计算机科学与技术学院，2012.Wang Jing.Research on acquisition System modeling based remote sensing image resolution improvement［D］.Nanjing:School of Computer Science and Technology，Nanjing University of Science and Technology，2012.