传递矩阵法分析平面柔顺机构的振动特性*
胡俊峰,郝亚洲,徐贵阳
(江西理工大学机电工程学院 赣州, 341000)
传递矩阵法分析平面柔顺机构的振动特性*
胡俊峰,郝亚洲,徐贵阳
(江西理工大学机电工程学院 赣州, 341000)
为了分析柔顺机构的动态性能和力学传递关系,提出一种新型的基于传递矩阵法的振动力学模型。柔顺机构由若干个柔性铰链与杆件顺序联接而成,采用传递矩阵法描述其力学状态量的传递关系。将柔性铰链视为拉伸和弯曲变形的弹性梁,应用材料力学理论建立反映其自振性能的传递矩阵。将杆件视为刚体,采用动量矩定理建立其动力学模型,得到描述振动刚体的传递矩阵。按照柔顺机构的联接形式,将每个元件的传递矩阵进行拼装,得到系统总传递矩阵。总传递方程以柔顺机构的边界点状态矢量为未知变量,矩阵中的元素为机构结构参数和频率的函数。应用边界条件,可得柔顺机构的特征方程,通过求解方程可得系统的固有频率和振型。将外力纳入传递矩阵,建立反映外力激励与系统的关系的扩展传递矩阵以求解系统的频率响应。通过2种常用平面柔顺机构的动态性能分析,结果表明所建立模型的正确性,能精确描述柔顺机构力学传递关系。
传递矩阵法; 力学模型; 动态性能; 平面柔顺机构
引 言
目前,高精度、高分辨率的精密微操作平台在近代尖端科学研究领域占有极其重要的地位。微操作平台作为微技术和机器人技术交叉结合的产物,主要用于精确控制微细操作。它的操作对象和微动部分的运动范围极小,可以完成其他机械无法实现的精细操作,如对细胞进行融合、存储、切割等细胞自动作业。在用于处理微小物体进行微细定位和加工操作时,微操作平台系统具有很大的优点,在微电子加工、装配与操作等超精密制造与作业领域,微操作平台也有广阔的应用前景[1-4]。
柔顺机构是一种利用构件的弹性变形传递或转换运动、力或能量的新型机构[5-7],具有运动分辨率高和运动精度高等特点,适宜于作为微操作平台的执行机构。但是,精密微操作平台易受外界环境扰动,为了消除外界环境的扰动,需要建立振动力学模型并对其动态性能进行分析。目前,建立柔顺机构的力学模型的方法主要为伪刚体法和有限元法。伪刚体法是将柔性铰链作为传统运动副并采用传统机构分析方法分析其力学性能,该方法适宜于描述柔顺机构的静态力学性能,同时该方法视铰链为理想铰链[7-9],所以其计算精度低。有限元法是将柔顺机构柔性铰链和杆件划分为按一定方式相互联结的单元,具有多个自由度,所以采用有限元法描述柔顺机构力学性能精度高,但计算量大,计算效率低,适宜于描述柔顺机构的静态和动态性能,但不便于分析机构参数与其性能之间的关系。
由于柔顺机构是复杂多刚-柔体系统,涉及矩阵阶次高、计算工作量大、计算出现“病态”的问题[10],而传递矩阵法具有无需系统的总体动力学方程、涉及的矩阵阶次低、建模灵活、程式化程度高等特点[11-12]。传递矩阵法通过拼装各个元件的传递矩阵得到系统的总传递矩阵,再利用边界条件得到系统的特征方程,对其求解得到系统的固有振动特性,所以传递矩阵法适宜于建立柔顺机构的振动力学模型。传递矩阵法根据动态响应的解析解导出的传递矩阵可精确描述柔顺机构的振动特性并得到其动态响应的精确解。与有限元法[13]和伪刚体法相比,传递矩阵法所建立的模型具有精确、简明、计算量小、物理意义清晰等特点。
笔者根据柔顺机构的结构特点,将柔顺机构分为2种元件,一种元件是直梁式柔性铰链,另一种元件为平面振动刚体,分别建立它们的传递矩阵,并得到系统的动力学方程。
1 柔顺机构振动力学模型
采用传递矩阵法建立柔顺机构的振动力学模型的主要思想是:将机构分解成易于用矩阵形式表达的简单力学特征元件。将每个元件按照它们相互之间的联接关系拼装得到整个系统的动力学方程。根据柔顺机构的结构特点,柔顺机构是由柔性铰链与杆件相互联接而成,分别建立柔性铰链与杆件的力学模型。假设柔顺机构是由直梁式柔性铰链和视为刚体的杆件构成,下面分别分析2种元件的传递矩阵。
1.1 直梁型柔性铰链传递矩阵
考虑直梁型柔性铰链尺寸较小,忽略其质量,同时在平面柔顺机构中,柔性铰链主要是纵向和横向振动,所以将其作为具有拉伸和弯曲变形的弹性梁。如图1所示,柔性铰链在纵向(x方向)和横向(y方向)振动,柔性铰链中任一点的状态矢量元素包括该点状态变量的位移与内力。设柔性铰链输入端与输出端的状态矢量分别为
(1)
其中:xh,I,yh,I,θh,I分别为铰链输入端的位移和转角;xh,O,yh,O,θh,O分别为铰链输出端的位移和转角;Mh,zI,Fh,xI,Fh,yI分别为铰链在输入端所受力和力矩;Mh,zO,Fh,xO,Fh,yO分别为铰链在输出端所受力和力矩。
定义柔性铰链的传递矩阵为其两端截面上的内力与位移的关系
Zh,O=UhZh,I
(2)
由柔性铰链平衡条件可知,力与力矩矢量和为零
(3)
其中:lh为铰链长度。
由材料力学可知,柔性铰链轴向变形[14]为
Δl=xh,O-xh,I=Fh,xIlh/EA
(4)
在柔性铰链x处的转角和变形为
(5)
其中:M(x)为在x处截面弯矩;C和D为积分常数,它们可由边界条件求得。
边界条件可表示为
(6)
由图1所示,采用截面法的截面弯矩可表示为
M(x)=Mh,zI+Fh,yIx
(7)
联合式(5)~式(7)可得柔性铰链输出端与输入端转角与位移的关系为
(8)
其中:E为弹性模量;A和I分别为柔性铰链的截面面积和惯性矩。
联合式(1)~式(4)和式(8)可得直梁型柔性铰链传递矩阵
(9)
由式(9)可知,柔性铰链的传递矩阵与其长度、截面惯性矩和弹性模量有关,反映了柔性铰链的自振性能。
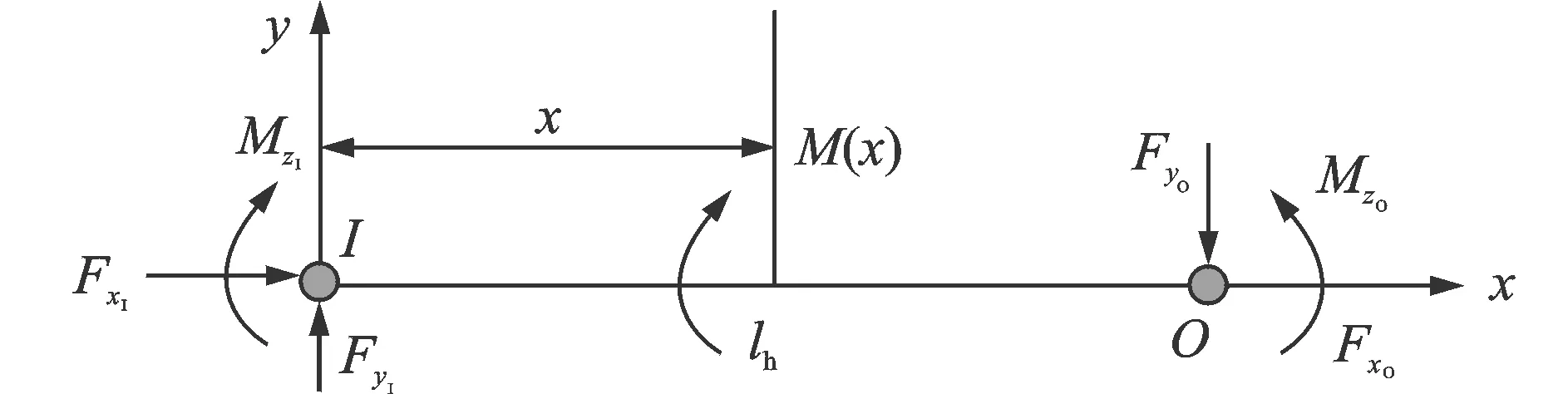
图1 直梁型柔性铰链模型
1.2 平面振动刚体传递矩阵
由于构成柔顺机构的杆件相对于柔性铰链尺寸较大,变形小,可视为平面振动刚体。定义杆件的输入点与输出点的状态矢量分别为
(10)
表示刚体输入与输出关系的运动微分方程,可得在频域中的平面振动刚体的传递矩阵
Zr,O=UrZr,I
(11)
如图2所示,一端输入一端输出平面振动刚体,质量为m,建立以输入点I为坐标原点的局部坐标系Ixy,刚体相对于点I的转动惯量为JI,输出点O的坐标为(bx,by),质心C点的坐标为(cx,cy)。根据输出点O与输入点I的几何关系,输出点O的转角与输入点I的转角相同,输出点O位移为
(12)
因转动的角度θr,I很小(θr,I≪1),则sinθr,I≈θr,I,cosθr,I≈1。所以,式(12)可写为
(13)
同理,可得质心C点的位移
(14)
根据质心运动定理和活动矩心绝对动量矩定理,可得平面振动刚体的动力学方程
(15)
联合式(12)和式(15)可得平面振动刚体的传递矩阵为
(16)
由式(16)可知,平面振动刚体的传递矩阵与杆件输出端和质心位置、质量、绕输入端的转动惯量及振动频率有关,反映了杆件的振动性能。
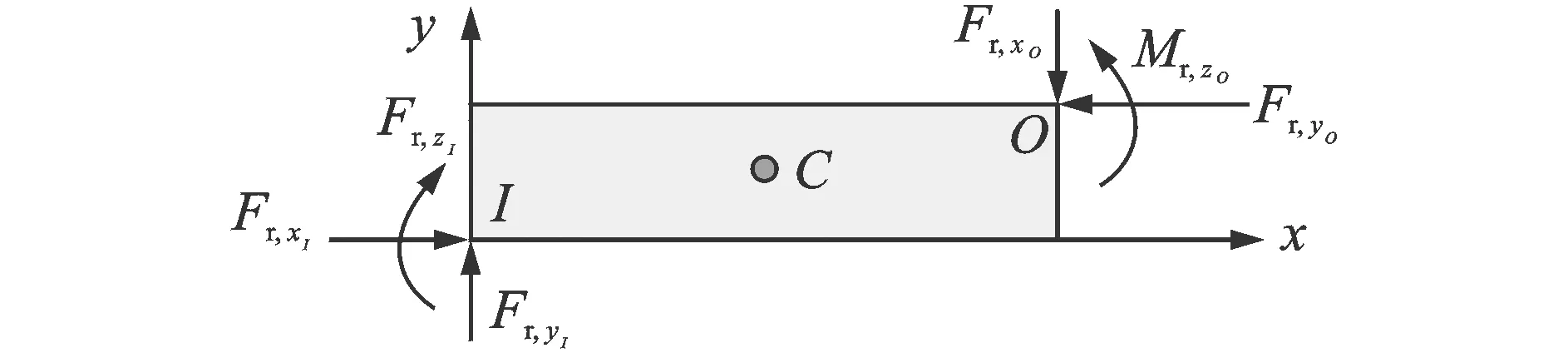
图2 平面振动刚体模型
1.3 坐标变换矩阵
基于大数据挖掘技术的智能变电站故障追踪架构//王磊,陈青,高洪雨,马志广,张艳杰,何登森//(3):84
(17)
其中:Ri为元件i的坐标变换矩阵。
研究平面柔顺机构振动时,若元件i状态矢量的形式表示为
(18)
(19)
将式(17)代入式(19)可得元件i在全局坐标系下的传递矩阵
(20)

图3 坐标变换
1.4 系统传递方程
如图4所示,设柔顺机构由n个元件(铰链和刚体)和n+1个联接点和边界点组成,Z1,I,Zn,O为边界点的状态矢量。
n个元件在全局坐标系下的传递方程分别为
(21)
由于元件1的输出是元件2的输入,依次类推,第i-1个元件的输出是元件i的输入,所以,系统的传递方程可以表示为
Zn,O=UZ1,I
(22)
其中
U=UnUn-1…Ui…U2U1
(23)
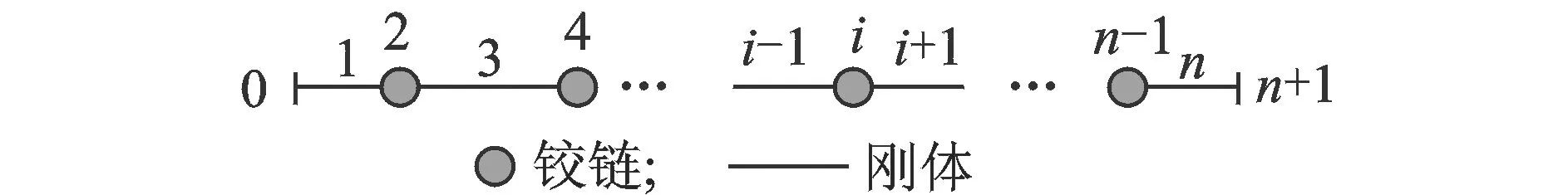
图4 柔顺机构总传递矩阵示意图
2 柔顺机构动态性能分析2.1 固有频率分析
采用系统的传递矩阵求解柔顺机构的固有频率。系统的传递矩阵的元素均为系统固有频率的函数。由式(22)表示的6个线性方程,应用边界条件,其中3个齐次方程可写为
(24)
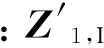
Δ=det(U′)=0
(25)
则Δ是关于ω的多项式函数,计算其根即为系统的固有频率。对每阶固有频率,可求解总传递方程得到系统边界点的状态矢量,利用每个元件传递矩阵得到系统每点的状态矢量和系统振型。
2.2 频率响应分析
采用传递矩阵法求解系统固有频率和振型后,可求解任意激励下柔顺机构的动态响应。设柔顺机构受频率为ω的简谐激励力,柔顺机构输出将以同样的频率ω作简谐振动,可得系统的频率响应。当ω=0所得出的响应为其静态响应。
为了将柔顺机构所受的外力纳入到传递矩阵,定义扩展状态矢量为
(26)
设柔性铰链处无外力作用,则对应于柔性铰链的扩展状态矢量的扩展传递矩阵为
(27)
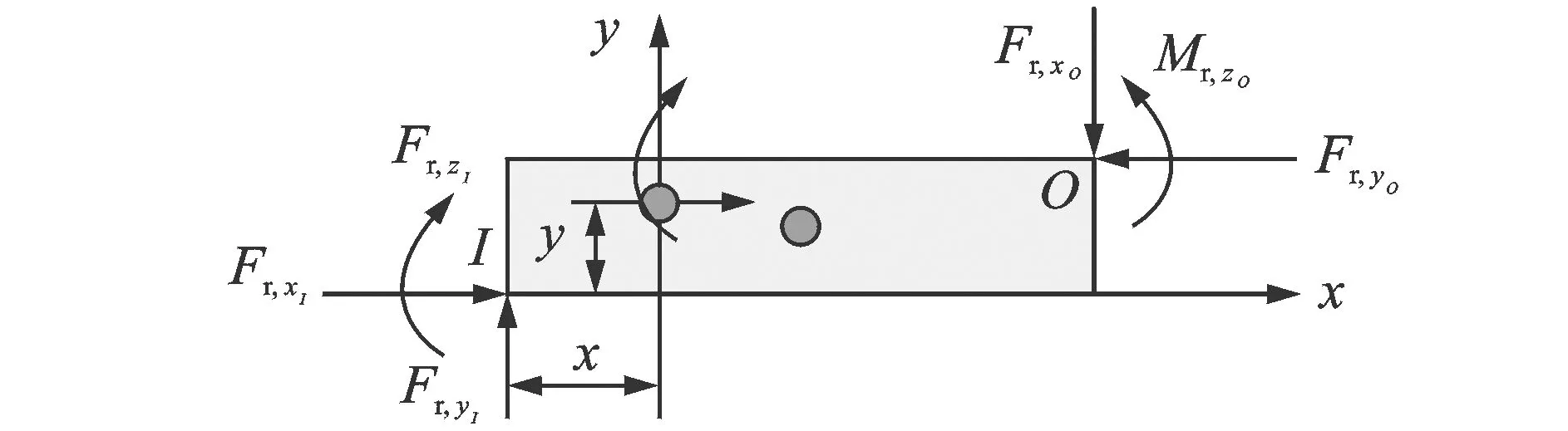
图5 平面振动刚体受力图
如图5所示,设在杆件某点(x,y)处受集中力和集中力矩,根据杆件的动力学方程可得
(28)
联合式(28)和式(26)可得杆件的扩展传递矩阵为
(29)
同理,由元件的传递方程得到系统稳态振动的总传递方程为
(30)
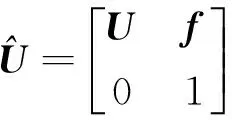
(31)
其中
利用边界条件,则可以得到柔顺机构输入端的状态矢量与外力及频率的关系,利用各个元件的传递矩阵就可得任何点的位移简谐响应。
3 算 例
3.1 导向柔顺机构
如图6所示,导向柔顺机构由导向梁和导向块组成,导向梁相对于导向块尺寸较小,视为直梁式柔性铰链,导向块为刚体。元件传递关系为1→2→3,可分别得出导向梁和导向块的传递矩阵,并根据各个构件的联接形式,则可得到整个系统总传递矩阵,可得元件1输入端和3输出端的状态矢量分别为
(32)
材料弹性模量E=200 GPa,密度ρ=7 850 kg/m3。Lg,tg和bg分别为导向梁的长度、厚度和宽度,它们分别为10,0.5和2 mm。导向块的长度、厚度和宽度分别为5,30和10 mm。
利用式(25)可求出导向机构的固有频率,为了研究分析柔性铰链参数对其固有频率的影响,各参数范围为Lg∈[5 20]mm,tg∈[0.1 2]mm和bg∈[1 10]mm,由于各个参数范围不一样,为了能比较分析,将它们进行归一化处理。图7表示导向机构固有频率与铰链参数之间的关系,由图可以看出,Lg和tg对导向机构影响较大,但bg对其影响较小,而且随Lg增大而减小,随tg增大而增大。分析结果符合导向机构工作特点,表明模型的正确性。
为了研究分析导向机构的振型,将第1阶固有频率代入各个元件的传递矩阵,并利用边界条件,可得各个点位移,将各个位移描绘可得如图8所示第1阶振型,实线表示机构静止时的状态,虚线表示系统的振型。由图可知,第1阶振型为沿y方向振动,与ANSYS模态分析的结果一致,说明所建立的模型的正确性。
为了分析导向柔顺机构的频率响应,设作用于如图6所示的输入力Fg=sinωt,频率范围为ω∈[102105]rad/s。根据系统的扩展总传递矩阵可得导向块沿y方向的位移简谐稳态响应,由此可得由输入力到输出位移的幅频响应曲线如图9所示。由图可知,当系统的激励频率接近于其固有频率,系统发生共振,说明所建立模型能精确反映导向机构的动态性能。
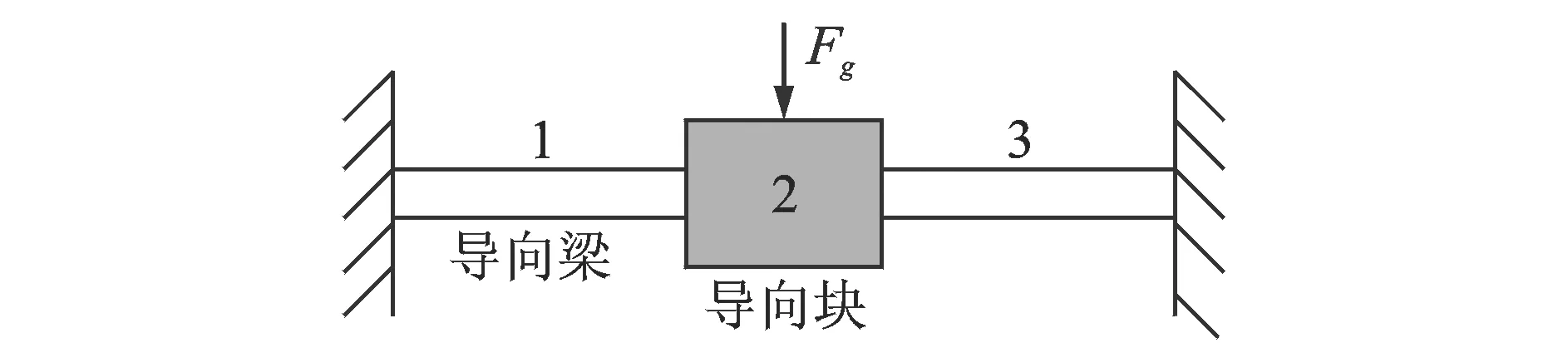
图6 导向柔顺机构
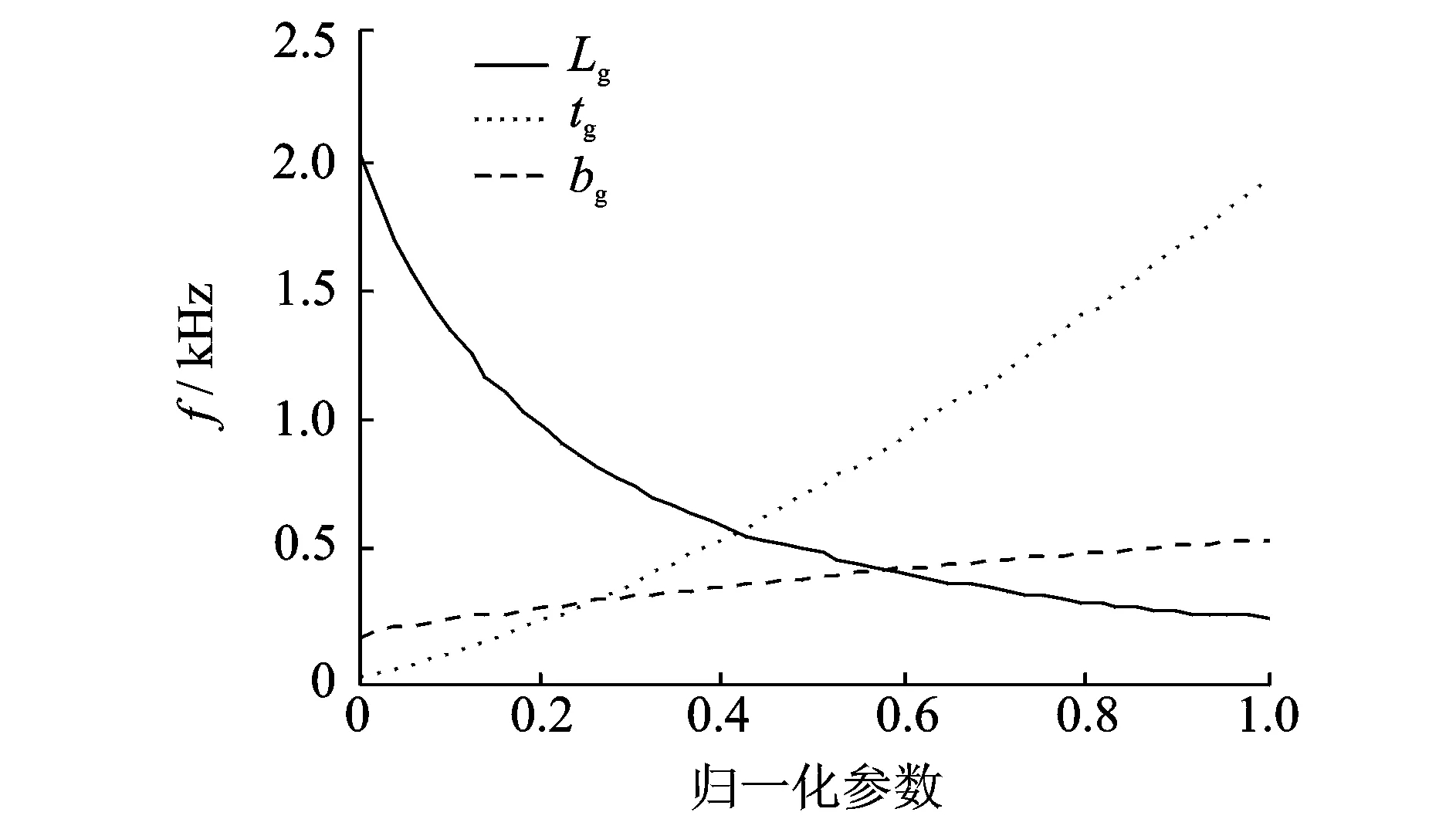
图7 导向机构固有频率与铰链参数之间关系
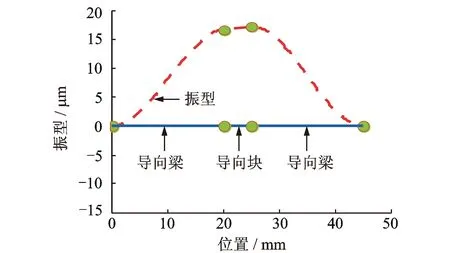
图8 导向柔顺机构第1阶振型
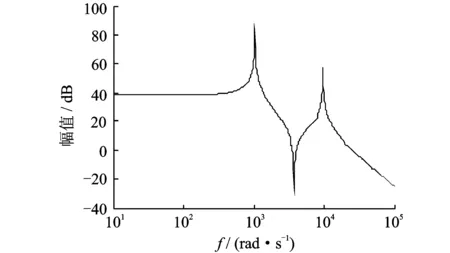
图9 导向机构幅频特性
3.2 桥式柔顺机构
桥式柔顺机构如图10所示,其采用桥式结构对进行位移放大,是一种常用的放大机构,机构由柔性铰链和杆件1,2及输出平台组成。设柔性铰链长、宽和高分别为3,10,0.6 mm,杆件1长和高分别为8,2 mm,杆件2长和高分别为18,7 mm,输出平台的长和高分别为8,3 mm。图11表示桥式柔顺机构的联接形式,元件传递关系为1→2→…→15。其中,元件1,3,…,13,15为直梁式柔性铰链,元件2,4,…,12,14为振动刚体,可分别建立它们的传递矩阵,系统的边界条件为
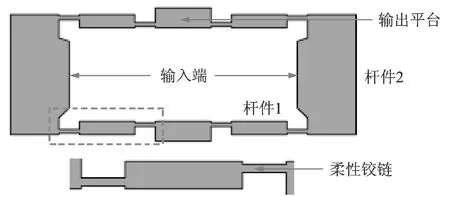
图10 桥式柔顺机构
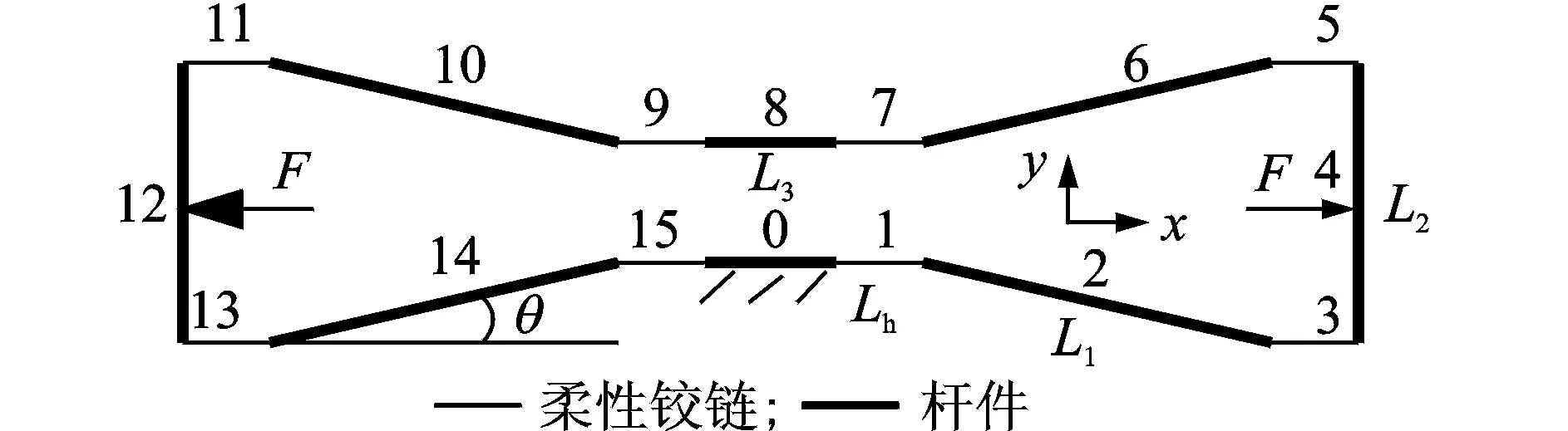
图11 桥式柔顺机构联接形式
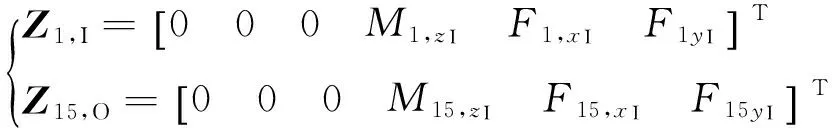
(33)
桥式柔顺机构的输入与输出之间关系为
(34)
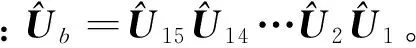
由边界条件,可求机构的固有频率和频率响应。通过求解桥式柔顺机构的特征方程可得系统的第1和2阶固有频率分别为1 516.6,4 263.2 rad/s。为了分析桥式柔顺机构的频率响应,设作用于如图11所示的输入力F=sinωt,其频率范围为ω∈[101104]rad/s。根据系统的扩展总传递矩阵可得输出平台沿x和y方向的位移稳态响应,由此可得由输入力到输出位移的幅频响应曲线,如图12所示。由图可知,当机构的激励频率接近于其固有频率时位移最大,y方向位移比x方向位移大,说明所建立模型能精确反映该机构的动态性能。
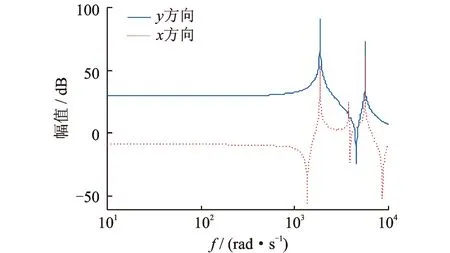
图12 桥式柔顺机构幅频特性Fig.12 The amplitude-frequency characteristic of bridge compliant mechanism
利用所推导出的扩展传递矩阵,可以对柔顺机构进行静态性能分析,即设ω=0,在单位力F=1作用下,利用传递矩阵的特点,可计算输入端与输出端的位移以及机构的放大倍数λ,结果为3.34,有限元ANSYS计算结果为3.67。两者计算的结果接近,表明理论模型的正确性。
4 结 论
1) 建立直梁型柔性铰链和杆件的传递矩阵,根据柔顺机构的结构特点,建立平面柔顺机构总传递矩阵,并利用边界条件建立系统的特征方程求解系统固有频率和振型。
2) 为了分析柔顺机构的频率响应,引入元件的扩展状态和扩展传递矩阵,将外力纳入传递矩阵,可求解系统的频率响应。
3) 对2种常用的平面柔顺机构进行动态性能分析,表明了所建立的动态模型的正确性。
[1] Choi K B, Lee J J, Hata S. A piezo-driven compliant stage with double mechanical amplification mechanisms arranged in parallel [J]. Sensors and Actuators A, 2010, 161: 173-181.
[2] 黄金永, 邓劲莲, 魏燕定. 具有抑振功能的超精密微动平台[J].机械设计, 2010, 27(7): 40-42.
Huang Jinyong, Deng Jinlian, Wei Yanding. Ultra-precision micro-displacement worktable with vibration suppression function [J]. Journal of Machine Design, 2010, 27(7): 40-42. (in Chinese)
[3] 余跃庆, 徐齐平, 周鹏. 复合载荷作用下柔顺机构的PR伪刚体新模型 [J]. 机械工程学报, 2013,49 (15): 9-14.
Yu Yueqing, Xu Qiping, Zhou Peng. New PR pseudo-rigid-body model of compliant mechanisms subject to combined loads [J]. Journal of Mechanical Engineering, 2013,49 (15): 9-14. (in Chinese)
[4] 王华伟,余跃庆,苏丽颖,等. 柔顺机构动力学建模新方法 [J]. 机械工程学报,2008,44(10):96-103.
Wang Huawei, Yu Yueqing, Su Liying, et al. New method for the dynamic modeling of compliant mechanism [J]. Journal of Mechanical Engineering, 2008,44(10):96-103. (in Chinese)
[5] 余跃庆,徐齐平. 柔顺机构PR伪刚体动力学建模与特性分析 [J]. 农业机械学报, 2013, 44(3): 225-229.
Yu Yueqing, Xu Qiping. Dynamic modeling and characteristic analysis of compliant mechanisms based on PR pseudo-rigid-body model [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(3):225-229. (in Chinese)
[6] 冯忠磊,余跃庆,王雯静. 模拟柔顺机构中柔顺杆件末端特征的2R 伪刚体模型 [J]. 机械工程学报,2011,47(1):36-42.
Feng Zhonglei, Yu Yueqing, Wang Wenjing. 2R pseudo-rigid-body model of compliant mechanisms with compliant links to simulate tip characteristic [J]. Journal of Mechanical Engineering, 2011,47(1):36-42. (in Chinese)
[7] 胡俊峰, 张宪民. 3自由度精密定位平台的运动特性和优化设计 [J]. 光学精密工程, 2012,20(12): 2686-2695.
Hu Junfeng, Zhang Xianmin. Kinematical properties and optimal design of 3-DOF precision positioning stage [J]. Optics and Precision Engineering, 2012, 20(12): 2686-2695. (in Chinese)
[8] Tian Yuanfeng, Shirinzadeh B., Zhang Daqiang, et al. Design and forward kinematics of the compliant micro-manipulator with lever mechanisms [J]. Precision Engineering, 2009, 33: 466-476.
[9] Hopkins J B, Culpepper M L. A screw theory basis for quantitative and graphical design tools that define layout of actuators to minimize parasitic errors in parallel flexure systems [J]. Precision Engineering, 2010, 34: 767-776.
[10]余跃庆. 柔顺机构学 [M]. 北京:高等教育出版社, 2007:113-116.
[11]万浩川, 李以农, 郑玲. 改进的结构振动传递矩阵法 [J]. 振动与冲击, 2013,32 (9): 173-177, 182.
Wan Haochuan, Li Yinong, Zheng Ling. Improved transfer matrix method in structural vibration analysis [J]. Journal of Vibration and Shock, 2013,32 (9): 173-177,182. (in Chinese)
[12]郭兰满,黄迪山,朱晓锦. 传递矩阵法分析轴向受力智能梁的振动和稳定性[J]. 振动、测试与诊断, 2011, 31(1):78-84.
Guo Lanman, Huang Dishan, Zhu Xiaojin. Transverse vibration and stability analysis of smart beam subject to axial force [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(1): 78-84. (in Chinese)
[13]占金青,胡俊峰,张宪民. 基于趋近律离散滑模控制的柔性梁振动抑制 [J]. 振动、测试与诊断, 2012, 32(2): 186-191.
Zhan Jinqing, Hu Junfeng, Zhang Xianmin. Vibration suppression of flexible beam based on discrete sliding mode control with reaching law [J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(2): 186-191. (in Chinese)
[14]秦飞. 材料力学 [M]. 北京: 科学出版社, 2012:83-87.

10.16450/j.cnki.issn.1004-6801.2015.06.023
*国家自然科学基金资助项目(51265016);江西省教育厅科技资助项目(GJJ12358);江西省自然科学基金资助项目(20122BAB216029)
2013-11-10;
2014-04-22
TH703; TP274
胡俊峰,男, 1978年10月生,副教授。主要研究方向为柔顺机构和结构动力学与控制。曾发表《3自由度精密定位平台的运动特性和优化设计》(《光学精密工程》2012年第20卷第12期)等论文。 E-mail: hjfsuper@126.com

