基于模糊集的作业车间预测调度研究
□赵攀
北京空间技术研制试验中心 北京 100094
在生产制造业中,作业车间在实际执行生产调度计划的过程中,会存在各种各样的不确定影响因素,如原材料短缺、设备故障、订单变更以及加工误差等[1],使车间生产实际处于一个动态变化的环境中。这些因素的存在往往会导致原有调度计划无法按预定的调度目标正常执行,因此,研究在该不确定因素下的预测调度问题成为了当前的研究热点。
陈宇等[2]分析了不确定性事件对生产过程的干扰和对调度过程的影响,提出了一种基于设备整体效能的具有鲁棒性的预测调度实现方法,设计了一种基于多Agent协作机制的预测调度系统模型。李巧云等[3]研究了可能遭遇机器故障的工件动态到达的单机总加权拖期生产调度问题,提出了一种带空闲时间阈值的预测调度方法,基于工件动态到达的特点,充分利用初始调度中的空闲时间,通过空闲时间阈值灵活控制空闲时间的插入与否。张沙清等[4]建立了以调度计划变更费用最小为优化目标的预测调度模型,并提出了不确定环境下多项目预测调度算法。针对作业车间的不确定性因素,模糊集理论已经成功应用于许多不确定性生产调度问题。文献[5-7]介绍了基于模糊逻辑的预测调度解决作业车间调度问题,在材料短缺情况下,应用模糊规则求解空闲时间的插入,进而生成预测调度。金宏等[8]应用模糊规则和模糊调度理论,提出一个基于模糊反馈控制的调度算法,并建立相应的调度架构。
本文针对材料短缺对工件加工过程的影响,以工件的最大完工时间为目标,建立基于模糊集的预测调度数学模型。应用遗传算法求解调度方案,找出预测调度在各机器上工件的加工顺序,再找到一种可行的最优调度方案,得到最合适的最大完工时间,使其具有一定的鲁棒性,能够吸收有限的材料短缺干扰。最后通过仿真程序验证模型及算法的可行性和有效性。
1 预测调度模型
假设以下条件。
(1)每个工件都包含一个由多道工序组成的工序集合,工件的工序加工顺序预先给定,每道工序对应一台确定的加工机器和一个加工时间 pji(j=1,...,N,i=1,...,M);
(2)每个工件都对应一种材料,同一工件各个工序用相同的材料;
(3)不同工件的工序之间没有顺序约束,每台机器在同一时刻只能加工一道工序,工序在加工过程中不允许中断。
在 M 台不同的机器 Mi(i=1,...,M)上加工 N 个不同的工件 Jj(j=1,...,N),在保证满足假设条件又考虑材料短缺的情况下,以工件的最大完工时间Cmax为目标,找出预测调度在各机器上工件的加工顺序,找到一种可行的最优调度方案。 Cmax=max{Cji|j=1,...,N;i=1,...,M},其中Cji表示工件Jj在机器Mi的加工时间 (Cji=pdji)。
预测调度是为了使材料短缺产生的可能不良影响最小化。在预测调度中,在每个工件的加工时间中插入空闲时间以生成扩展加工时间的方法来吸收调度过程中一定的材料短缺干扰。工件Jj在机器Mi上的加工时间为 pdji,pdji=pji+idji( j=1,...,N;i=1,...,M),其中 idji表示预测调度为工件Jj每个工序插入的空闲时间,它是生产过程中每标准时间段内材料短缺发生次数的模糊数和材料短缺持续时间的模糊数之积,标准时间是工件每个工序平均加工时间。有G种不同的材料mg(g=1,...,G)参与加工过程。 材料 mg的短缺发生次数用离散有限集 NOCg表示,NOCg={nocg1,nocg2,...,nocgK}。标准时间内工件Jj所用材料mg短缺发生次数的模糊数用模糊集Og表示,其模糊数用μOg(nocgk)/nocgk表示,即 Og={[μog(nocgk)/nocgk|k=1,...,K]} ,如图 1 所示。每次材料短缺持续时间用关于模糊集Rg(trg)的连续梯形函数 μRg
(trg)表示,该连续函数由(trg1,trg2,trg3,trg4)4个参数决定,如图2所示。

▲图1 材料短缺发生次数模糊集
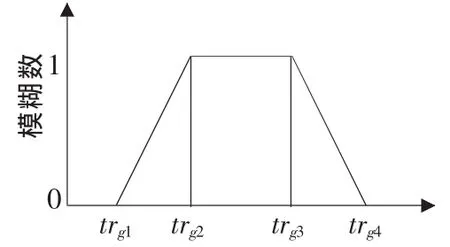
▲图2 材料短缺持续时间模糊集
用离散模糊集Og和连续模糊集Rg的模糊乘法[4]计算被干扰工件标准时间段内总的材料短缺时间,即用二级模糊集Og⊗Rg来计算:
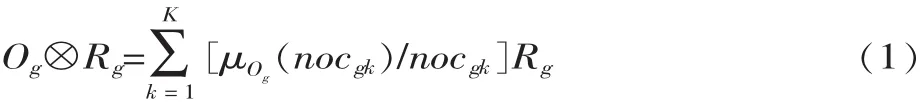
为了准确计算每个工序的加工时间pji中加入的空闲时间idji,首先将二级模糊集转换为标准模糊集,即将二级模糊集Og⊗Rg转化为标准模糊集s-fuzzif(Og⊗Rg)[5],标准模糊集函数方程为:

然后将标准模糊集应用重心法逆模糊化[4],用tdg值表示标准时间段内材料短缺持续时间,则:
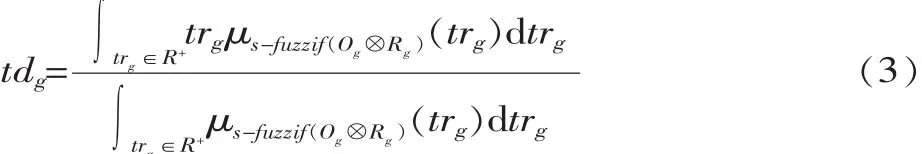
发生 4 次材料中断的例子为:NOCg={1,2,3,4},
Og=0.7/1+1.0/2+0.4/3+0.25/4,Rg(trg)的梯形函数所组成的二级模糊集示例如图3所示,则:
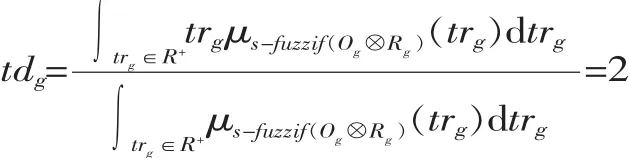
根据逆模糊化tdg计算插入到工件Jj工序i的空闲时间idji,idji=tdgpji/STD,其中STD为逆模糊参数常量。
当空闲时间idji确定后,将其加入到每个工序的加工时间pji中,应用遗传算法生成预测调度。预测调度产生基准调度方案后,下发到生产车间指导生产,任务开始按序加工。在干扰发生之前,生产车间的所有机器上实际调度和预测调度的工件加工顺序是相同的。
2 调度算法

▲图3 材料mg在一定模糊数下总短缺时间的模糊值
调度模型确定后,预测调度及反应式调度都应用遗传算法[9,10]求解。算法的基本思想是:首先采用基于优先列表编码方式进行编码,在该编码方式下随机生成初始种群;其次对种群进行评价,评价的适应度函数为最小化最大加工时间};评价后对种群进行选择、交叉、变异操作,然后对种群进行精英选择生成新一代群体,循环,直至达到最大进化代数结束,其具体过程如下。
2.1 编码
基于编码效率的考虑,本文采用基于优先列表的编码方式。基于优先列表的编码方式的染色体由M条子染色体组成,每个子染色体对应1台机器,即对具有M台机器的车间调度问题,基于优先列表编码方式的染 色 体 可 以 描 述 为 : [σ1,σ2,...,σM]。 其 中 :σi=[ki1,ki2,...,kiM] 为机器 Mi(i=1,2,...,M)对应的子染色体,表示在机器Mi上待加工工件(相应操作)的加工优先表,kij(i=1,2,...,mj)为在机器 Mi上待加工工件的工件号,表示在机器Mi上待加工工件Jkji的 相 应 操 作 ,kij∈[1,2,...,N] ,且若 x≠y,则 kjx≠kjy,mi为在机器 Mi上待加工工件(相应操作)的总数。
2.2 初始种群产生
随机产生一种加工模式,针对该加工模式随机产生n个加工方案,对n个加工方案进行解码,然后将加工模式和加工方案组成一个二维向量染色体X,该种方式产生的染色体都是一个较优的可行解,如此循环产生最优染色体作为初始种群{x1,...,xn}。
2.3 选择操作
本文利用二元锦标赛方法对排序较优的N个个体进行选择,以进行后续的交叉、变异。二元锦标赛选择法是一种基于染色体适应度排序的选择方法,每次在若干染色体中,选择适应度最高的一个染色体,且重复N次来得到由N个染色体组成的新一代种群。在选择过程中,染色体是否被选择只与染色体之间适应度的相对大小有关,而与其具体适应度无关。
二元锦标赛选择法的流程可描述如下。
步骤1:在种群中随机选取 2条染色体,然后选择其中适应度最大的染色体;
步骤2:重复步骤 1,共N次,得到由 N条染色体组成的新一代种群。
2.4 交叉操作
对于优秀种群,随机选择出两个染色体作为父代个体 X1、X2,通过交叉产生两个子代个体 X1′、X2′,这里采用两点交叉算子来生成子个体。
对于父代个体X1、X2,随机产生两个交叉点xp1和xp2,xp1≠xp2。通过交换两交叉点之间的部分,得到子个体。图4给出两点交叉的示意图。
2.5 变异操作
针对本文研究问题的编码方式,采用逆操作作为变异算子,即随机选择染色体上某一机器对应的基因片段,然后将片段上的基因串逆。如对于 3×3问题的变异示意图如图 5所示,迭择机器2上的基因片段做逆序操作。
变异操作后新个体的控制方案可以唯一确定控制成本,但其加工方案却不一定是最优加工方案。对新个体进行局部搜索优化,此时保持个体控制方案不变,对加工方案进行禁忌搜索,以完全遍历禁忌列表作为终止原则,寻找局部最优加工方案,提高种群质量。
2.6 精英进化策略
在较优解的基础上进行交叉、变异操作获得优秀后代个体的机率比较大,因此在产生新种群时,基于精英保留策略将根据偏序关系得到的优秀个体复制进入下一代,加快获得最优解,提高求解效率。利用优秀个体进行交叉变异产生新的子代个体,将优秀个体X整体作为操作对象,这样新种群中引入新染色体的概率比较大,提高了种群的多样性,避免了种群早熟。

▲图4 个体互换交叉示意图

▲图5 个体逆序变异示意图
3 实验结果及分析
本节以在6台机器上加工6个工件为例来分析模糊规则在车间作业预测调度中的应用,并使用C++编程进行仿真分析。
每个工件需要用一种材料,则需要6种材料,每种材料的标准时间段分别为 9 h、8 h、5 h、3 h、9 h、7 h;标准时间内插入的空闲时间分别为6 h、5 h、3 h、1 h、3 h、5 h。
根据第3节的模糊集可以计算扩展加工时间,见表1。

表1 工件扩展加工时间/h
工件在机器上的加工顺序:工件1为机器4、机器1、机器 2、机器 3、机器 6、机器 5;工件 2 为机器 6、机器 3、机器 5、机器 2、机器 1、机器 4;工件 3为机器 6、机器 4、机器 3、机器 2、机器 5、机器 1;工件 4为机器5、机器 1、机器 3、机器 4、机器 2、机器 6;工件 5 为机器 3、机器 2、机器 5、机器 6、机器 1、机器 4;工件 6 为机器 5、机器 4、机器 2、机器 1、机器 3、机器 6。
每个工序的空闲时间插入到各工序中得到扩展加工时间后,应用遗传算法来生成预测调度工序排列方案和完工时间。遗传算法中,种群大小为100;进化代数为100;染色体是基于优先列表编码、采用随机机制产生;选择算子采用二元锦标赛选择;交叉算子采用两点互换交叉,交叉概率为0.8;变异算子采用基于优先列表的通用二进制变异方法,变异概率为0.1。遗传算法对每个工件在机器上进行排序生成预测调度,预测调度工序排列方案和完工时间见表2和表3。
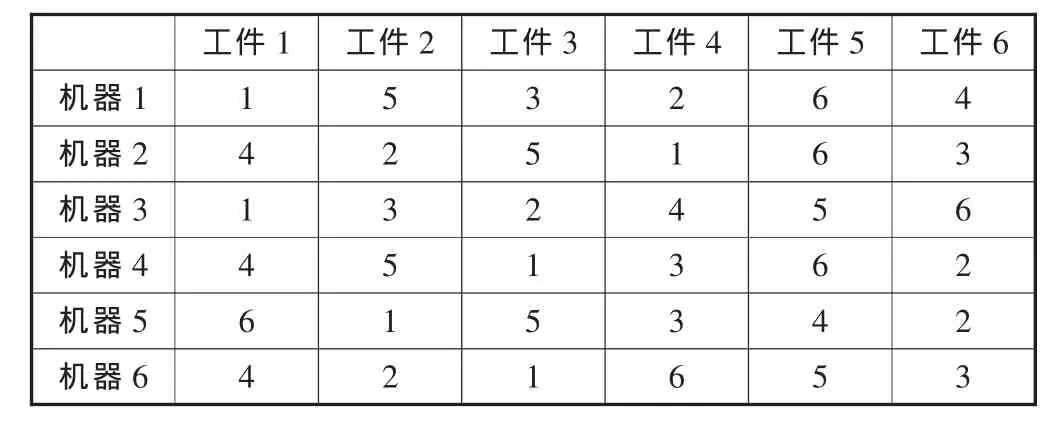
表2 最优解工序排列方案
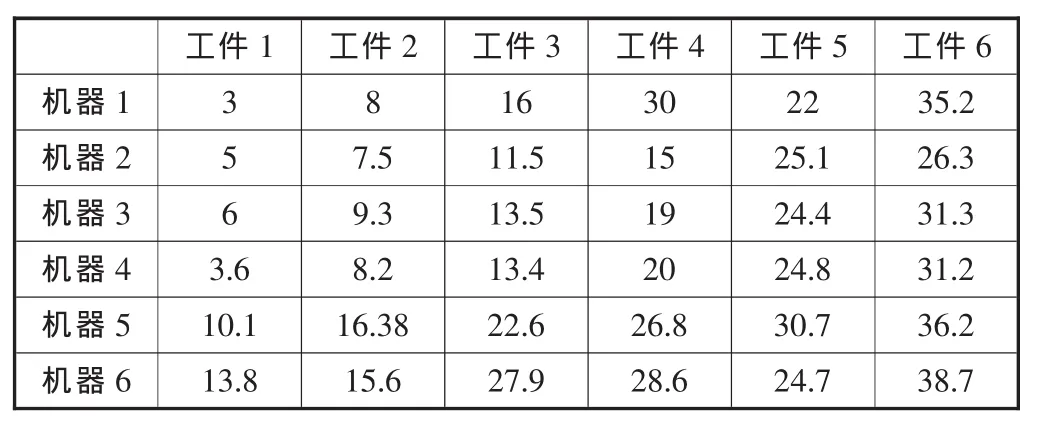
表3 各工件最优完工时间/h
4 结论
本文建立了基于模糊集的预测调度数学模型,并应用遗传算法找出了预测调度在各机器上工件的加工顺序,找到了可行的最优调度方案,以在6台机器上加工6个工件为例验证了模型和算法的可行性。结果表明,当材料短缺发生时间不大于最大完工时间的五分之一,预测调度能够吸收有限的材料短缺干扰,使其具有一定的鲁棒性,因此对预测调度性能的影响不大。
[1] Niu Ganggang,Sun Shudong,Lafon Pascal,etal.A Predictive-reactive Approach forJSP with Uncertain Processing Times [C].In Research in Interactive Design:Virtual,Interactiveand Integrated ProductDesign and Manufacturing for Industrial Innovation,Paris,2010.
[2] 陈宇,陈新,陈新度,等.基于设备整体效能和多 Agent的预测-反应式调度[J].计算机集成制造系统,2009,15(8):1599-1605.
[3] 李巧云,王冰,王晓明.随机机器故障下单机预测调度方法[J].系统工程理论与实践,2011,31(12):2387-2393.
[4] 张沙清,陈新度,陈庆新,等.资源不确定环境下模具多项目预测-反应式调度算法[J].计算机集成制造系统,2010,16(12):2688-2696.
[5] Petrovic D,Duenas A.A Fuzzy Logic Based Production Scheduling/rescheduling in the Presence ofUncertain Disruptions [J].Fuzzy Sets and Systems,2006,157 (16):2273-2285.
[6] Duenas A,Petrovic D.An approach to Predictive-reactive Scheduling of Parallel Machines Subject to Disruptions [J].Annals of Operations Research,2008,159(1):65-82.
[7] Petrovic S,Petrovic D,Burke E.FuzzyLogicBased Production Scheduling/Rescheduling in the Presence of Uncertainty [J].Planning Production and Inventories in the Extended Enterprise,2011,152:531-562.
[8] 金宏,王宏安,傅勇,等.模糊反馈控制实时调度算法[J].软件学报,2004,15(6):791-798.
[9] 周明,孙树栋.遗传算法原理及应用 [M].北京:国防工业出版社,1999.
[10]王凌.车间调度及其遗传算法 [M].北京:清华大学出版,2003.

