基于Workbench的无隔离环超越离合器片弹簧强度与疲劳分析

□ 徐燚伟 □ 初长祥， □ 高 晓 □ 王松林 □ 梁永华

1.广西科技大学 机械工程学院 广西柳州 545006

2.广西柳工机械股份有限公司 广西柳州 545007

常见的ZL50装载机通常匹配的是双涡轮行星式变速箱,它主要是通过滚柱式超越离合器与液力变矩器联合使用。其中滚柱式超越离合器（以下简称超越离合器）可以根据负载的变化自动把输入一、二级齿轮（即Ⅰ、Ⅱ涡轮）的两个动力整合为中间输入轴的一个输出。图1所示为无隔离环超越离合器结构，其中片弹簧为每个滚柱提供压紧弹簧力，且与滚柱之间呈线接触关系，受力均匀，相比普通弹簧而言，它更能保障滚柱与内外圈处于良好的啮合状态［1］。

装载机的作业工况复杂多变，完成一次装载任务包括以下步骤：前进-铲料-倒车-前进靠近卡车-卸料-倒车-停车。在一次循环过程中，超越离合器需要完成8次锁止和分离，大约需要耗时45 s［2］。超越离合器每一次的楔紧和分离，片弹簧都要进行一次压缩和回弹。装载机无故障使用周期按照8 000 h设计，对于无隔离环超越离合器的片弹簧需要满足512万次压缩、回弹。可见片弹簧在超越离合器及整个传动系统中有着重要作用。

本文使用Pro/E建立片弹簧三维模型，并将模型导入到Workbench有限元分析软件中进行静力结构分析，结合材料的应力-寿命曲线，使用Fatigue Tool模块对其进行静力结构分析和疲劳寿命仿真分析。

1 建立有限元模型

▲图1 无隔离环超越离合器的组成

▲图2 片弹簧基本结构及参数

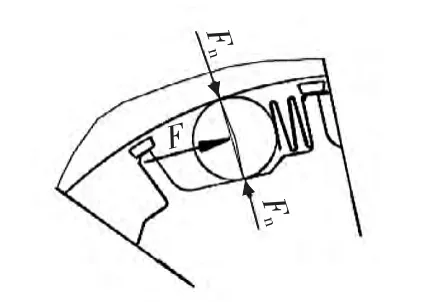
▲图4 无隔离环超越离合器片弹簧受力模型

▲图3 片弹簧的三维网格模型

如图2所示，片弹簧基本参数：自由长度H=11 mm,厚度 h=0.115 mm,宽度 b2=10 mm,高 b=40 mm,折弯次数4折，折弯处过渡圆弧R=0.75 mm，折弯角度θ=20.64°。使用Pro/E构建片弹簧三维设计模型，然后导入到Workbench对其进行有限元分析。考虑到片弹簧的压缩变形量是其厚度的数十倍，也为了保证计算结果的精确度，采用了一些措施：①采用正六面体单元进行网格划分［3］，图3为片弹簧的三维网格模型（由于片弹簧高度上是对称的，为便于分析计算，取原模型1/4高度）；② 在分析计算时,打开 “大变形”，即：将“Solver Controls”中的“Large Deflection”处于“On”状态。

图4所示为无隔离环超越离合器片弹簧受力模型，片弹簧是通过挡板压紧在超越离合器的内星轮上，用来防止其轴向和径向的窜动。由于滚柱与片弹簧之间是线接触的关系，且沿片弹簧长度方向空间受力均匀。因此，为了准确模拟片弹簧的受力情况，将片弹簧一端施加“Fixed Support”，在另一端的3/5处 ，即弹簧与滚柱接触位置，施加垂直载荷Fn。

2 静力结构分析

片弹簧是保证离合器的滚柱与内外圈处于良好啮合状态的重要压紧元件，故对其刚度有特定的要求，既不能太大也不能太小。过大会造成解楔的困难，使离合器内外圈分离迟滞；过小又会造成啮合效率低，离合器打滑，进而造成离合器传动失效。同时，在整个工作过程中，片弹簧应力变化次数多，变化幅度较大。因此，片弹簧要具有良好的弹性、韧性和塑性。本文选用SUS301不锈钢，其强度极限为1 324 MPa,屈服极限为1 030 MPa，弹性模量E为206 GPa，泊松比为0.3。

2.1 刚度计算

2.1.1 有限元分析

依据内星轮结构,计算出片弹簧与滚柱之间的预紧力为 10.06 N［4］，经过 Workbench分析求解得到如图5所示片弹簧的等效总变形云图。根据弹簧刚度的定义和Workbench有限元分析，片弹簧的最大位移量4.127 4 mm，片弹簧刚度2.44 N/mm。

▲图5 片弹簧等效总变形云图

▲图6 片弹簧受力分析简化模型

2.1.2 理论分析

假设片弹簧在工况下压缩弹簧时处于完全弹性阶段，无塑性变形，因此有变形能U等于外力做功W，即：W=U。

根据材料力学中能量法推导片弹簧的刚度和变形能计算公式：

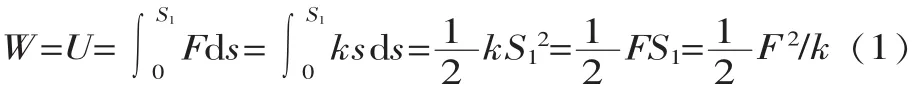
式中：k为片弹簧刚度，N/mm；F为片弹簧受力，N；S为片弹簧变形（0～S1），mm。

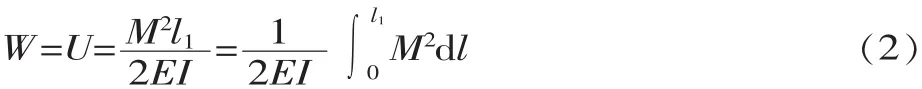
式中：I为片弹簧截面惯性矩，I=bh3/12，mm4；M 为受力点的弯曲力矩，N·mm；l为受力点到支撑点间的距离（0～l1），mm。

由于滚柱与片弹簧之间是线接触的关系，且沿片弹簧长度方向空间受力均匀。因此，可将片弹簧简化为平面受力模型进行分析,即图6所示的由圆弧和直线构成的线弹簧问题。其中：L为平直悬臂长度，r为过渡圆弧半径，α为片弹簧每两折之间夹角的1/2，β为过渡圆弧圆心角的1/2，φ为圆弧上某一点到圆弧起始位置的夹角（取值范围 0～β）。在悬臂BC段任意截面所受的弯曲力矩为：

式中：x为BC段某点到C点间的距离 （取值范围0～L）。

在过渡圆弧AB段弯曲力矩为：

将式（3）代入式（2）,可得在BC段变形能为:

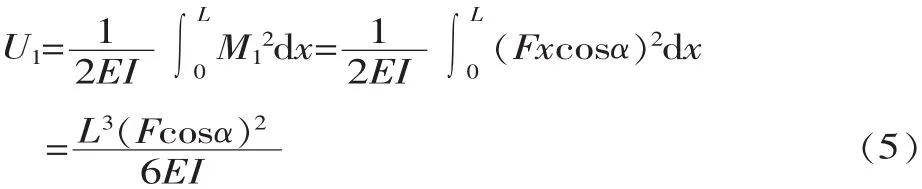
将式（4）代入式（2），可得在过渡圆弧AB段弯曲变形能为：

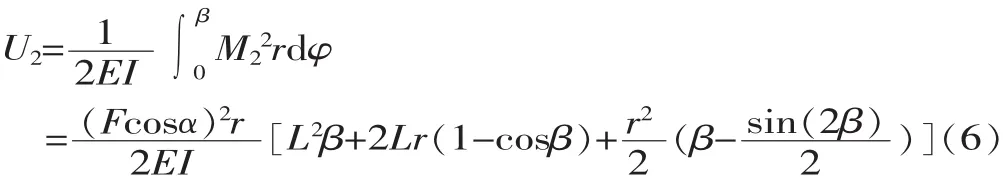
由式（5）和式（6）可得ABC段弯曲变形能为：

将式（7）代入式（1），可知理论计算刚度为：

奇数折刚度计算：k1= 3EI

［L3+3rL2β+6Lr2（1－cosβ）+3r3

2（β－sin（2β）2）］cos2α

（9）

偶数折刚度计算：

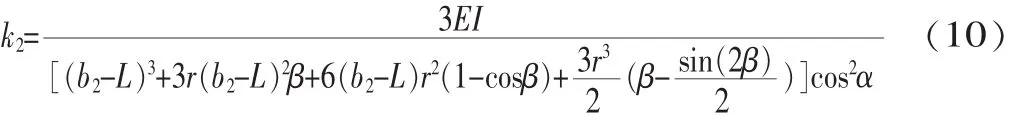
2.2 片弹簧应力分析

2.2.1 有限元分析

片弹簧三维网格模型经过Workbench分析求解得到图7所示的片弹簧等效应力云图。根据图示应力分布情况可知：从施加载荷位置起，应力向片弹簧折弯处扩展，每一折的施加载荷位置的应力最小；片弹簧应力最大值出现在每一折的折弯处，最大应力为655.23 MPa；根据屈服极限1 030 MPa计算出屈服强度安全系数ns=1.57，大于安全系数推荐值 1.4［5］，则应力满足设计要求。

▲图7 片弹簧等效应力云图

2.2.2 理论分析

当片弹簧承受滚柱施加的压力时，片弹簧最大应力出现在图6片弹簧受力分析简化模型所示A点处。即：

其中：Kσ为片弹簧弯曲部分应力集中系数［6］； h/（2R）如图8所示；Zw为片弹簧的抗弯截面系数，ZW=bh2/6，mm3。

3 疲劳寿命分析

在Workbench仿真分析中，Fatigue疲劳模块拓展程序是基于应力疲劳理论，它适用于高周疲劳［7］。片弹簧的最大应力相对其屈服极限小很多,对于应力通常比材料的极限强度低的情况，其主要失效形式是高周疲劳破坏。因此，本文将使用应力疲劳理论的处理方法对片弹簧的疲劳寿命进行分析。

3.1 应力－寿命曲线

载荷与疲劳失效关系是通过应力－寿命曲线（S-N曲线）来表示，如图9所示为SUS301不锈钢片弹簧的S-N（Semin－log）曲线。根据实验测得的应力－寿命曲线通常是对材料的试件做弯曲或轴向疲劳测试获取的单轴应力状态。然而，在实际工况下，部件可能处于多轴应力状态。同时，影响应力－寿命曲线有诸多因素，如平均应力影响，试件的表面几何结构影响，施加载荷环境影响等。因此疲劳仿真设计需要引入平均应力修正理论，从而将定义的单轴应力状态的S-N曲线转化为考虑平均应力影响。

▲图8 片弹簧弯曲部分应力集中系数

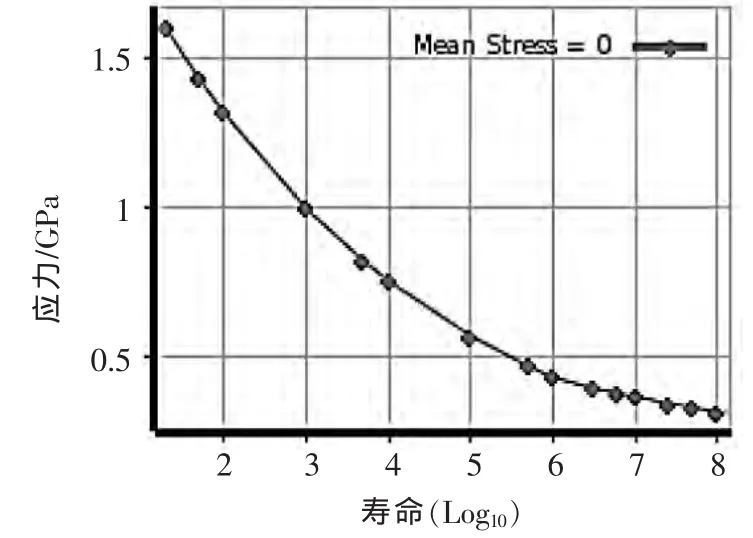
▲图9 片弹簧的S-N（Semi－log）曲线.

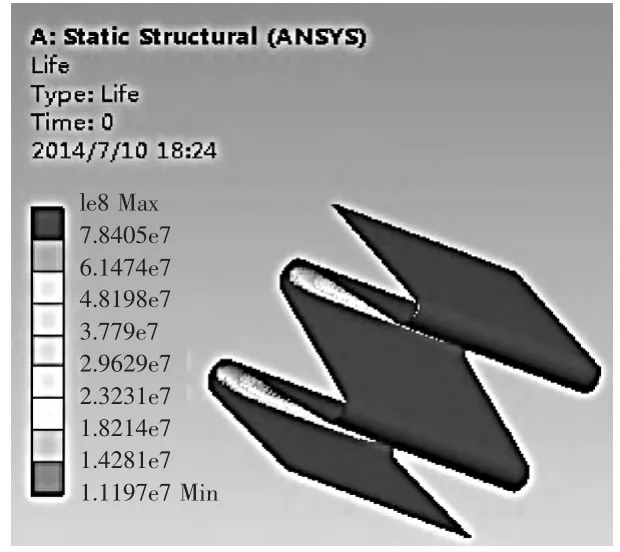
▲图1 0 片弹簧等效寿命云图

3.2 疲劳分析

用Workbench进行疲劳分析是基于线性静力分析理论，并且需要输入材料的S-N曲线。在Workbench的Fatigue Tool模块下确定载荷类型“Ratio”,平均应力的修正理论“Soderberg”，应力成分“Equivalent （Von Mises）”和实际部件与试件差异性的强度因子”Kf”。

图10为片弹簧等效寿命云图，图11为片弹簧等效损伤云图，是Workbench仿真分析软件分别从寿命和损伤这两个角度对片弹簧进行分析计算结果。分析云图 表明：片弹簧的最薄弱点出现在折弯处，最少可以承受1 119.7万次压缩、回弹；片弹簧设计寿命与可用寿命最大比值约为0.46。此分析结果验证了片弹簧符合512万次压缩、回弹的设计要求。

4 结论

（1）片弹簧结构简单、便于安装固定，能使滚柱受力均匀，保障滚柱与内外圈处于良好的啮合状态，有利于提高无隔离环超越离合器的使用寿命。

（2）根据表1片弹簧有限元解和理论解比较，有限元分析结果和理论计算结果相差很小，最大的应力误差也仅是1.86%。可见，Workbench的分析结果精度较高。

表1 片弹簧有限元解和理论解比较

（3）Workbench静力学分析和理论分析结果具有一致性,片弹簧的最大应力出现在其折弯角处。根据Workbench的疲劳寿命分析，片弹簧的最小寿命和最大损伤值出现在其折弯角处，此结构的片弹簧可以满足至少512万次的疲劳寿命要求。同时，Workbench有限元分析软件为此类强度和寿命分析问题的解决和改进提供了一种有效途径，具有一定的实际指导意义。

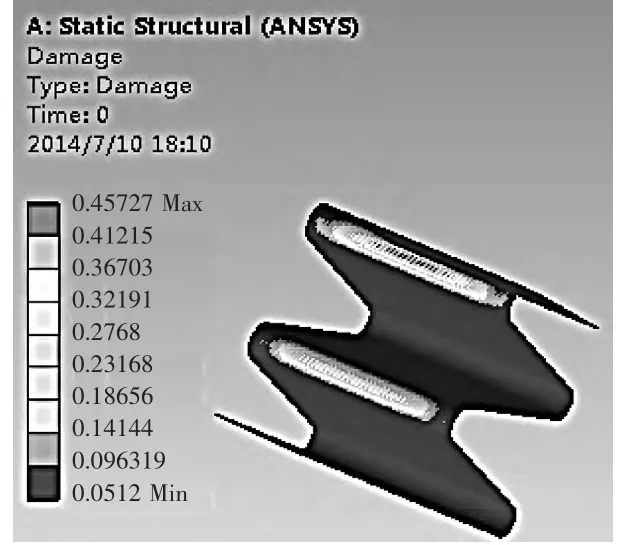
▲图1 1 片弹簧等效损伤云图

［1］ 樊琳.片弹簧结构超越离合器［J］.机械制造，1996（10）:12.

［2］ 王松林,马文星,胡晶，等.双涡轮液力变矩器超越离合器的改进及分析［J］.吉林大学学报,2013,43（7）：922-927.

［3］ 曲昌荣,巢凯年.钢板弹簧有限元分析［J］.轻型汽车技术,2005（10）;15-16.

［4］ 成大先.机械设计手册（第2卷）［M］.北京：化学工业出版社,2008.

［5］ 徐灏.机械强度设计中的安全系数和许用应力［J］.机械强度，1981（2）：39-45.

［6］ 张英会,刘辉航,王德成.弹簧手册［M］.北京：机械工业出版社,2010.

［7］ 兰洪波.旋转导向工具片弹簧强度与疲劳分析［J］.天然气技术,2010，4（5）：47-49.