异步控制Varicol工艺分离愈创木酚甘油醚对映体过程研究
龚如金,林小建,李平,于建国
(华东理工大学化学工程联合国家重点实验室,上海 200237)
引 言
手性对映体药物进入生物体后往往在药效学、药代动力学等方面呈现很大的差异,因此美国、欧共体、日本等许多国家相继颁布关于手性药物生产的法规,这些举措极大地促进了手性药物拆分技术的发展。获得光学纯度高且毒副作用小的单一对映体已经成为医药研究的发展方向。模拟移动床(SMB)色谱具有成本低、分离效率高、固定相利用率高、流动相循环使用、自动化连续操作等优势,已被国际上公认为制备规模拆分手性药物的最有效手段[1-4]。
为了提高模拟移动床的分离效率,适应更复杂的分离体系,在传统的模拟移动床技术基础上发展出了一些新的技术,主要包括梯度模拟移动床(溶剂、温度)[5-6]、超临界模拟移动床[7]、各区色谱柱数量变化Varicol工艺[8]、进料浓度可变的Modicon工艺[9]、流动相流速可变的Powerfeed工艺[10]、 三区SMB[11]、五区SMB[12],此外还有模拟移动床串联技术[13]、模拟移动床技术与结晶耦合[14]等。工艺的不断发展和创新使得 SMB技术更加完善,在分离技术领域更有竞争力。
Varicol工艺是对传统SMB技术的一种改进,操作原理基于循环周期内进出口位置的不同步切换。与传统模拟移动床相比,Varicol工艺各区中的色谱柱分布随时间变化,而且柱数不受整数的限制,从而提高各区中固定相的利用率,节省手性固定相的使用,降低分离成本。与使用相同数量色谱柱的SMB工艺相比[15],Varicol工艺分离效果更好,而且在设计和操作上灵活性更高。然而,由于Varicol过程离散的动态切换对分离区域有很强的影响,并且该工艺对实验设备自动化控制要求较高,目前研究工作大多是基于数值计算,实验研究相对较少[8,15-21],而国内理论和实验研究报道更少。黄永东等[22]采用传统SMB、Varicol、Partial-discard工艺通过实验分离纯化ECG和EGCG,结果表明:同传统SMB相比,Varicol工艺具有提高产品纯度和回收率的优点。Lu[23]通过建立异步切换SMB模型,利用文献数据验证了模拟结果,并理论分析了异步切换过程的优势,模型和数值方法可以用来确定 Varicol工艺合适的操作条件。肖迪等[24]设计了16种典型的Varicol运行模式,并通过数值方法从轴向浓度分布曲线分析了Varicol工艺的优势。
在前期工作中[25],通过实验和理论计算比较了SMB和Varicol两种工艺分离愈创木酚甘油醚对映体的效率,结果发现Varicol工艺分离效果更好,更适用于手性药物分离,但是对于Varicol工艺的设计及分离过程并没有进行详细的理论研究。本研究采用 Varicol工艺的数学模型计算了愈创木酚甘油醚对映体在系统内浓度分布的时间进程曲线,分析Varicol工艺的分离过程,并设计了5柱 (1-1.5-1.5-1)构态的 Varicol工艺分离愈创木酚甘油醚对映体的操作区,通过Varicol实验进行了验证。
1 数学模型
模拟移动床以逆流连续操作方式,通过同步切换物料进出口位置实现吸附剂向下移动而物料向上移动的效果,提高了固定床的生产能力和分离效率,同时避免了移动床中吸附剂移动产生的磨损。而Varicol工艺与SMB工艺区别在于:
(1)SMB的切换周期为ts,而本研究采用的5柱(1-1.5-1.5-1)Varicol工艺在ts内又分为二步,在整个循环内Varicol工艺增加了切换步骤;
(2)SMB工艺在循环内每个区内柱数不变,而Varicol随切换过程每个区内的柱数会发生改变,提高了SMB的分离效率。
模拟移动床色谱数学模型是由色谱柱模型和柱与柱之间起衔接作用的节点模型所构成。模型的基本假设为:
(1)整个过程温度恒定,没有热效应,并且忽略吸附热对谱带的影响;
(2)不考虑色谱柱内部径向浓度、速度分布,只考虑轴向上的质量、动量传递过程;
(3)填料及床层空隙率分布均匀,忽略手性固定相颗粒内部的传质过程;
(4)假设色谱柱内流动为平推流,忽略流动相的可压缩性,组分在色谱柱内以恒定的线速度运动;
(5)组分在流动相中传播时,分子扩散和涡流扩散综合为轴向扩撒,而且扩散系数恒定。
为了能够描述分离的动态过程以及进出口的异步切换,采用模拟移动床模型的建模方法。Varicol工艺使用的模型方程与模拟移动床一样,区别在于Varicol工艺考虑了进出口位置的异步切换模式,同时也考虑了轴向扩散和传质阻力的影响,并且采用线性驱动力模型描述固定相颗粒上的传质过程[18,19,26-28],模型方程见表1。
2 数学模型求解
在实际操作中 5柱(1-1.5-1.5-1)Varicol工艺的运行方式为:0~0.5ts时间内按照SMB(1-1-2-1)运行,0.5ts~ts时间内按照 SMB(1-2-1-1)运行,如图1所示。所以在数值求解过程中一个切换周期可以看成 SMB(1-1-2-1)和 SMB(1-2-1-1)的耦合。
表1中的偏微分方程和代数方程构成了Varicol工艺过程的数学模型。Varicol工艺过程中,由于进出口位置的异步切换,每根色谱柱在切换周期内表现为不同的功能区,节点位置处的边界条件也随之发生改变。在gPROMS编程环境下,通过直线数值方法对Varicol工艺数学模型进行数值求解。以时间作为连续变量,采用有限元正交配置法对空间变量进行离散,沿色谱柱轴向方向将床层分为 50个单元,每个单元采用3个配置点,将偏微分方程组转化为常微分方程组。两相邻有限元通过相邻配置点的连续条件关联得到,边界条件上的配置点代入边界条件。使用DASOLV求解器对常微分方程组和代数方程组进行求解,迭代过程中绝对误差限为10−5。此外, 对比有限元正交配置法和有限元差分法发现离散方法对模拟结果影响不大。

表1 Varicol工艺数学模型方程Table 1 Mathematical model equations for Varicol process

图1 Varicol(1-1.5-1.5-1)工艺分离过程的数值求解方法Fig.1 Numerical solution method of Varicol process(1-1.5-1.5-1)
3 结果讨论
前期工作[29]已经测定了愈创木酚甘油醚对映体(R-GUA,S-GUA)在Chiralcel OD固定相上的吸附平衡以及模型参数(表 2),其中组分 R-GUA为弱保留组分,组分 S-GUA为强保留组分,流动相为正己烷/乙醇=70:30(体积比),柱温为25℃。本研究采用的Varicol工艺由5根色谱柱串联,填充的固定相粒径为20 μm,柱构态为1-1.5-1.5-1,进料质量浓度为 4 mg·ml‒1。
3.1 进出料口异步切换对多柱内R-GUA和S-GUA浓度分布的影响
本研究通过数值方法考察初始循环内 Varicol工艺异步切换模式对R-GUA和S-GUA浓度分布的影响,如图2所示,模型参数和工艺条件见表2。横坐标反映了 Varicol工艺进出料口在循环内异步切换的过程。从初始状态开始需要总共经过 10步切换,才能完成一次5柱(1-1.5-1.5-1)Varicol工艺完整的循环。在系统进料前,吸附分离过程尚未开始,所有色谱柱处在初始状态即浓度为零(t=0)。随后系统通过进料口开始连续不断地进料,组分在床层内发生吸附脱附过程,在第一次切换之前系统内瞬态内部浓度曲线如图所示(t=0.5ts)。随着进出料口位置的不断切换,强吸附组分 S-GUA逐渐移动到萃取液口位置,而弱吸附组分 R-GUA逐渐移动到萃余液口位置,两组分实现分离。

表2 Varicol工艺操作条件和模型参数Table 2 Operating conditions and model parameters of Varicol process
在表 2的操作条件下,通过数学模型预测 20个循环内愈创木酚甘油醚对映体内部浓度曲线,如图3所示。经过5次循环后循环开始趋于稳定,此时内部浓度曲线随循环数增加不再发生变化。结果表明Varicol工艺分离R-GUA和S-GUA对映体时系统能够快速达到稳定状态。此外,通过数学模型还预测了萃取液和萃余液两个出口中溶质的浓度曲线随时间的变化,如图4所示。在一次切换周期内,萃余液出口 R-GUA组分浓度随时间增大,萃取液出口 S-GUA组分浓度随时间降低,并且在一个循环内呈周期性变化。

图2 初始循环阶段Varicol工艺的柱内R-GUA和S-GUA瞬间浓度分布Fig.2 Transient internal concentration profile for R-GUA and S-GUA in first cycle of Varicol process
3.2 分离区设计及实验验证
通过在数学模型中考虑进出料口位置的异步切换模式,三角形操作区可以指导Varicol工艺的分离过程[17,30]。为了保证 1区内强吸附组分 S-GUA从吸附剂上全部脱附,同时在4区内保证弱吸附组分R-GUA全部被吸附,m1和m4必须满足一定的约束条件。对于Langmuir型吸附等温线,一种简化的方法可以用来确定m的约束值[31-32],见式(1)和式(2)。本实验设计中选取m1=5.79,m4=1.61。通过数值方法,在满足99.0%产品纯度要求的前提下设计的Varicol工艺分离操作区如图5所示,设计条件以及模型参数见表 2。在理论上认为此区域内均能获得至少99.0%的产品纯度。
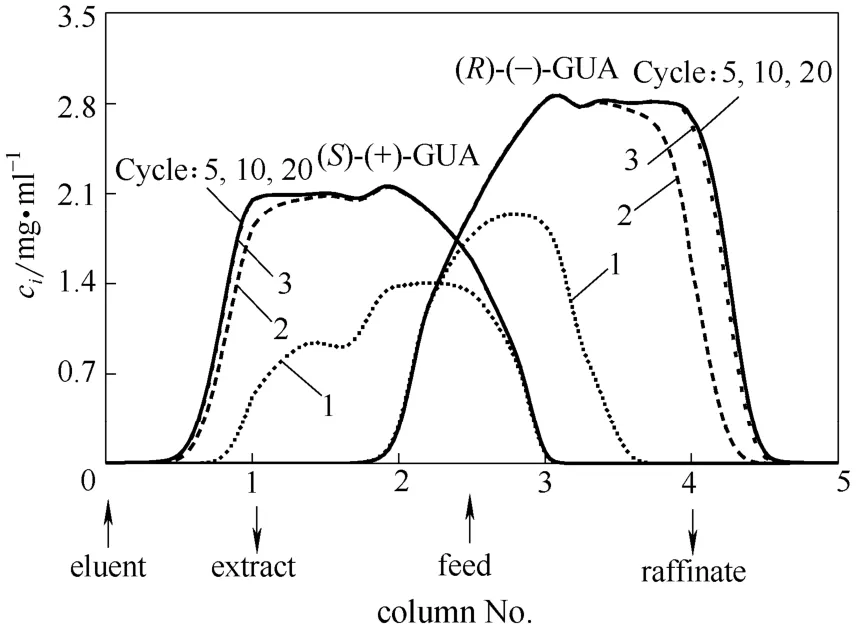
图3 不同循环内Varicol工艺内部浓度曲线(操作条件见表2)Fig.3 Internal concentration profile of Varicol process at half switch time with different cycles (operating conditions shown in Table 2)
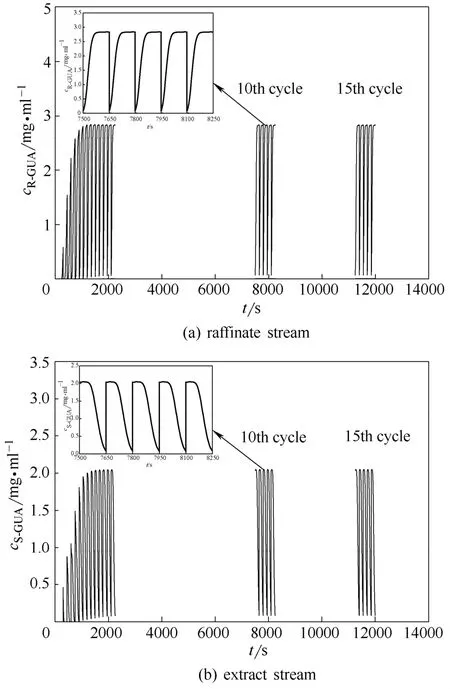
图4 Varicol工艺15个循环内产品流出曲线Fig.4 Concentration profile of Varicol process for 15 cycles in raffinate stream and extract stream (top left corner is outlet streams during the 10th cycle)
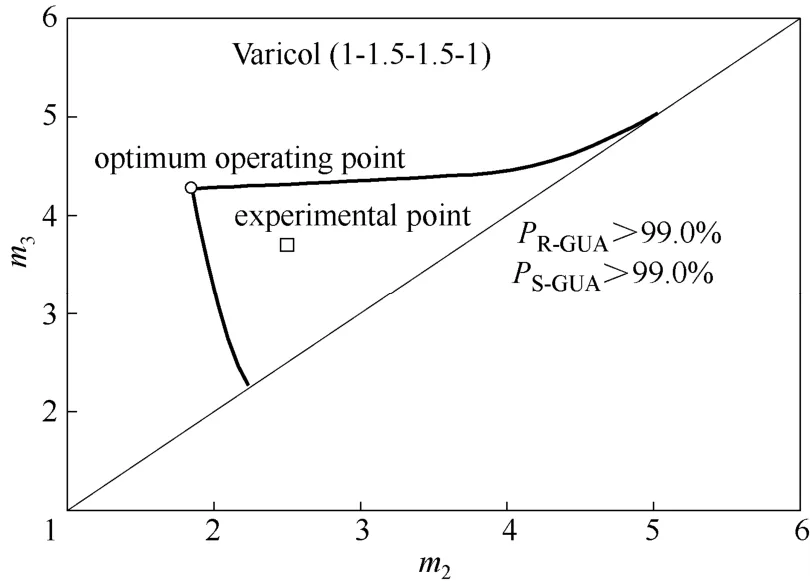
图5 Varicol工艺(1-1.5-1.5-1)分离愈创木酚甘油醚对映体的操作区Fig.5 Separation region of 1-1.5-1.5-1 Varicol process for guaifenesin enantiomers

参数mj为液相净流速和固相净流速之比,定义见式(3)。

为了验证设计的分离操作区,在其内部选取实验操作条件,在 MICRO-VARICOL仪器上进行Varicol实验。相应的实验操作条件和实验结果见表3[25]。比较实验和模拟结果,虽然实验结果略低于理论预测的纯度,但是仍然满足设计的99.0%纯度要求。数学模型能够较好地预测Varicol工艺分离过程,而且设计的分离操作区可以用来指导 Varicol(1-1.5-1.5-1)工艺分离愈创木酚甘油醚对映体的设计与优化。

表3 Varicol工艺各区的流速及分离愈创木酚甘油醚对映体的实验和模拟结果比较Table 3 Flow rates in each zone of Varicol process and comparison of separation results between experiment and simulation for separation of guaifenesin enantiomers
选择实验点居于三角形区域中心主要是考虑到此位置相对于区域边缘部分的抗干扰性较强,选择这样的操作点对于初始设计能够获得比较理想的实验结果。理论上,三角形顶点位置的分离性能最好,产率最高,并且溶剂消耗量最低。但是在实际分离中,由于死体积以及模型参数等因素的影响,该操作点的最佳分离性能往往难以实现,因而操作点往往会选择靠近该顶点的位置。
在实际过程中除了扩散作用还有传质阻力的影响,这些都影响三角分离区的变化。Pais等[31]报道了传质阻力对模拟移动床操作分离区的影响,结果证明随传质阻力增大操作分离区的区域减小。另外,系统死体积会引起三角操作区位置的偏移[33]。针对本研究选择的分离体系,吸附分离因子较大,约为 2.6。当进料浓度较低时,非线性竞争型Langmuir吸附作用不强,设计的三角形操作区域较大,如图5所示,采用Varicol工艺很容易分离愈创木酚甘油醚。增加进料浓度,非线性作用变强,实际的操作区域变得越窄,愈创木酚甘油醚分离操作条件选择越严格。
4 结 论
针对Chiralcel OD为手性固定相、乙醇/正己烷为流动性相的 Varicol工艺分离愈创木酚甘油醚对映体体系,建立了异步切换的Varicol过程的数学模型,采用有限元正交配置法对模型进行数值求解。该模型能够较好地预测愈创木酚甘油醚对映体在模拟移动床多个色谱柱内的浓度曲线分布。随着进出料口位置的不断切换,强吸附组分(S)-对映体(S-GUA)逐渐移动到萃取液口位置,弱吸附组分(R)-对映体(R-GUA)逐渐移动到萃余液口位置。当多次循环操作(如10次)后,系统达到稳定状态,优化工艺条件,在萃取液口位置能够回收高纯度的S-GUA,在萃余液口位置能够回收高纯度的R-GUA。
由动态切换的 Varicol工艺的数学模型计算愈创木酚甘油醚分离操作区,选择高纯度对映体(99%R-GUA和99% S-GUA)分离条件。基于设计的操作条件,进行5柱Varicol工艺(1-1.5-1.5-1)的分离愈创木酚甘油醚对映体实验。结果表明,S-GUA和 R-GUA两个组分实现了 99.0%的高纯度的分离结果,满足设计要求,与理论预测基本吻合。因此建立的数学模型能够较好地预测愈创木酚甘油醚对映体的Varicol工艺分离过程,为工业化设计提供基础理论依据。
符 号 说 明
ci,k——组分i在第k根色谱柱中的液相质量浓度,kg·m−3
Dax,i——轴向扩散系数,m2·s−1
F——相比[F= ( 1 −εT)/εT],m2·s−1
j——区数(j=1,2,3,4)
KL——传质系数,m·s−1
k——柱子数目(k=Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ)
Lk——第k根色谱柱长度,m
mj——第j区净流速比
qeq,i,k——组分在固相中的质量浓度,kg·m−3
——与液相浓度平衡时的固相质量浓度,kg·m−3
t——时间,s
ts——切换时间,s
u——线速度,m·s−1
Vc——色谱柱体积,m3
v1,v2,v3,v4——1~4 区内的间隙流速,m·s−1
z——轴向坐标,m
εT——总孔隙率
[1]Li Ling (李凌), Jing Yuanwei (井元伟), Yuan Decheng (袁德成).Simulated moving bed adsorption separation technology and its applications [J].Computers and Applied Chemistry(计算机与应用化学), 2007, 24 (4): 441-444
[2]Cai Yujie (蔡宇杰), Ding Yanrui (丁彦蕊), Zhang Dabing (张大兵),Dai Jun (戴军), Shi Guiyang (石贵阳), Xu Wenbo (须文波).Simulated moving bed technology and its applications [J].Chinese Journal of Chromatography(色谱), 2004, 22 (2): 111-115
[3]Wei Feng (危风),Shen Bo (沈波),Chen Mingjie (陈明杰),Zhou Xianbo (周先波),Wu Pingdong (吴平东). Omeprazole resolution by simulated moving bed chromatography [J].Journal of Chemical Industry and Engineering(China)(化工学报), 2005, 56 (9):1699-1702
[4]Rajendran A, Paredes Galatea, Mazzotti M. Simulated moving bed chromatography for the separation of enantiomers [J].Journal of Chromatograpy A, 2009, 1216: 709-738
[5]Li P, Xiu G H, Rodrigues A E. Proteins separation and purification by salt gradient ion-exchange SMB [J].AIChE Journal, 2007, 53:2419-2431
[6]Migliorini C, Wendlinger M, Mazzotti M, Morbidelli M. Temperature gradient operation of a simulated moving bed unit [J].Industrial Engineering Chemistry Research, 2001, 40: 2606-2617
[7]Peper S, Lubbert M, Johannsen M, Brunner G. Separation of ibuprofen enantiomers by supercritical fluid simulated moving bed chromatography [J].Separation Science and Technology, 2002, 37:2545-2566
[8]Toumi A, Hanisch F, Engell S. Optimal operation of continuous chromatographic processes: mathematical optimization of the VARICOL process [J].Industrial & Engineering Chemistry Research,2002, 41: 4328-4337
[9]Schramm H, Kaspereit M, Kienle A, Seidel-Morgenstern A.Simulated moving bed process with cyclic modulation of the feed concentration [J].Journal of Chromatography A, 2003, 1006: 77-86
[10]Zhang Z Y, Mazzotti M, Morbidelli M. Power feed operation of simulated moving bed units: changing flow-rates during the switching interval [J].Journal of ChromatographyA, 2003, 1006: 87-99
[11]Shen B, Chen M J, Jiang H L, Zhao Y X, Wei F. Modeling study on a Three-zone simulated moving bed without zone Ⅰ [J].Separation Science and Technology, 2011, 46: 695-701
[12]Wang X, Ching C B. Chiral separation of beta-blocker drug (nadolol)by five zone simulated moving bed chromatography [J].Chemical Engineering Science, 2005, 60: 1337-1347
[13]Wankat P C. Simulated moving bed cascades for ternary separations[J].Industrial & Engineering Chemistry Research,2001, 40:6185-6193
[14]Lorenz H, Sheehan P, Seidel-Morgenstern A. Coupling of simulated moving bed chromatography and fractional crystallization for efficient enantioseparation [J].Journal of Chromatography A, 2001,908: 201-214
[15]Ludemann-hombourger O, Nicoud R M. The “varicol” process: a new multicolumn continuous chromatographic process [J].Separation Science and Technology, 2000, 35: 1829-1862
[16]Ludemann-Hombourger O, Pigorini G, Nicoud R M, Terfloth G.Application of the ‘VARICOL’ process to the separation of the isomers of the SB-553261 racemate [J].Journal of Chromatography A, 2002, 947: 59-68
[17]Toumi A, Engell S, Ludemann-Hombourger O, Nicoud R M, Bailly M. Optimization of simulated moving bed and Varicol processes [J].Journal of Chromatography A, 2003, 1006: 15-31
[18]Zhang Y, Hidajat K, Ray A K, Morbidelli M. Multiobjective optimization of SMB and Varicol process for chiral separation [J].AIChE Journal, 2002, 48: 2800-2816
[19]Zhang Y, Hidajat K, Ray A K. Multi-objective optimization of simulated moving bed and Varicol processes for enantio-separation of racemic pindolol [J].Separation and Purification Technology, 2009,65: 311-321
[20]Da Silva A C, Salles A C, Perna R F, Correia C R D, Santana C C.Chromatographic separation and purification of mitotane racemate in a Varicol multicolumn continuous process [J].Chemical Engineering Technology, 2012, 35: 83-90
[21]Rodrigues R C R, Araujo J M M, Eusebio M F J, Mota J P B.Experimental of assessment of simulated moving bed and Varicol processes using a single-column setup [J].Journal of Chromatography A, 2007, 1142: 69-80
[22]Huang Yongdong (黄永东), Jiang Heyuan (江河源), Jiang Yongwen(江用文), Zhang Jianyong (张建勇), Wang Bin (王斌), Bai Yan (白艳), Wen Zhihao (文志浩), Wang Weiwei (王伟伟). Comparison of Varicol and partial-discard process with traditional process to purify ECG and EGCG from green tea polyphenols using simulated moving bed chromatography [J].Journal of Tea Science(茶叶科学), 2011, 31(3): 201-210
[23]Lu J G. Numerical simulation of asynchronous simulated moving bed chromatography [J].Chinese Journal of Chemical Engineering, 2004,12: 415-420
[24]Xiao Di (肖迪), Ge Qicheng (葛启承), Lin Jinguo (林锦国).Dynamic simulation of simulated moving bed based on Vericol [J].Computers and Applied Chemistry(计算机与应用化学), 2012, 29:567-570
[25]Gong R J, Lin X J, Li P, Yu J G, Rodrigues A E. Experiment and modeling for the separation of guaifenesin enantiomers using simulated moving bed and Varicol units [J].Journal of Chromatography A,2014, 1363: 242-249
[26]Yang Minglei (杨明磊), Wei Min (魏民), Hu Rong (胡蓉), Ye Zhencheng (叶贞成), Qian Feng (钱峰). Modeling of simulated moving bed for xylene separation [J].CIESC Journal(化工学报),2013, 64 (12): 4335-4341
[27]Wu Xiandong (吴献东), Jin Xiaoming (金晓明), Su Hongye (苏宏业).Multi-objective optimization of simulated moving bed chromatography separation based on NSGA-Ⅱ algorithm [J].Journal of Chemical Industry and Engineering(China)(化工学报), 2007, 58 (8):2038-2044
[28]Li Ling (李凌), Yuan Decheng (袁德成), Jing Yuanwei (井元伟).Simulated moving bed process modeling and performance analysis [J].Computers and Applied Chemistry(计算机与应用化学), 2013, 30(11): 1289-1293
[29]Gong R J, Lin X J, Li P, Yu J G, Rodrigues A E. Adsorption equilibrium and kinetic study of guaifenesin enantiomers on cellulose tris 3,5-dimethylphenylcarbamate packed column [J].Chemical Engineering Journal, 2014, 244: 128-136
[30]Pais L S, Rodrigues A E. Design of simulated moving bed and Varicol processes for preparative separations with a low number of columns[J].Journal of Chromatography A, 2003, 1006: 33-44
[31]Pais L S, Loureiro J M, Rodrigues A E. Separation of enantiomers of a chiral epoxide by simulated moving bed chromatography [J].Journal of Chromatography A, 1998, 827: 215-233
[32]Zhang Y, Hidajat K, Ray A K. Enantio-separation of racemic pindolol onα1-acid glycoprotein chiral stationary phase by SMB and Varicol[J].Chemical Engineering Science, 2007, 62: 1364-1375
[33]Migliorini C, Mazzotti M, Morbidelli M. Simulated moving-bed units with extra-column dead volume [J].AIChE Journal, 1999, 45:1411-1421

