问题 反思 改进——一次说题比赛的感悟

盛耀建 (湖州中学 浙江湖州 313000)



问题 反思 改进
——一次说题比赛的感悟

盛耀建 (湖州中学 浙江湖州 313000)

笔者有幸参与了2014年浙江省湖州市的说题比赛，切身体会到了教师说题的价值和意义.比赛结束后，笔者所在学校的名师工作室指导组成员对这次比赛情况进行了精彩地点评，受益匪浅.说题主要体现在说题目、说背景、说解法、说变化、说功能这5个方面.笔者以自己的参赛题目为例，从这5个方面对本次说课比赛进行了整理和反思，请同行指正.

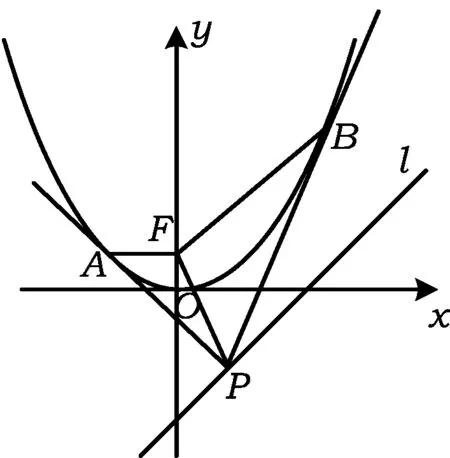
图1

题目 如图1，设抛物线C：y=x2的焦点为F，动点P在直线l：x-y-2=0上运动，过点P作抛物线C的2条切线PA,PB，且与抛物线C分别相切于点A,B.

1)求△APB的重心G的轨迹方程；

2)证明：∠PFA=∠PFB.

问题1 解答步骤不完整.

说题比赛的第一关是正确解答出题目，而正确的一个标准即是过程完整，若关键步骤漏了，那这次说题比赛必定是不成功的.

教师1在说第2)小题的解答时，将解题过程展现到

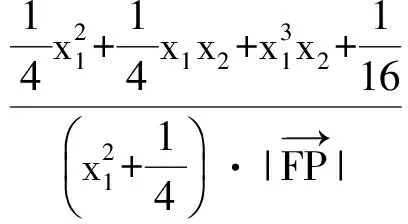
同理可得cos∠PFB的值，经检验发现相等，从而证得∠PFA=∠PFB，便嘎然而止.

运用向量运算并化简约分得

同理可得

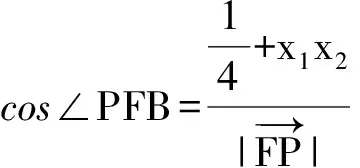
故由cos∠PFA=cos∠PFB，知∠PFA=∠PFB.

问题2 处理方法太单一.

在说题比赛中，由于题目有难度，造成解题时间仓促，思考时间不充足，因此大多数参赛选手仅能给出1种正确解答.

反思 针对说题过程中说解法这一环节，为了能够吸引评委和观众的注意，需尽可能地找出题目的多种解法，可以从思维方法角度，也可以从计算方法角度进行阐述，解法的多样化将会成为很大的得分点.

改进 多角度思考，会发现这道题的2个小题均有多种解法.

代入直线l的方程：x-y-2=0，得

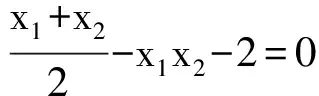
由重心坐标公式知

解法2 设P(x0,x0-2)，过点P的切线方程为

y=kx-kx0+x0-2，

代入y=x2,得

x2-kx+kx0-x0+2=0,

从而

Δ=k2-4x0k+4x0-8=0.

设切线PA,PB的斜率为k1,k2，则

分析 解法1从切点A，B的坐标出发，求出点P的坐标，代入直线l的方程得到x1+x2与x1x2的关系，利用重心坐标公式求出重心轨迹方程；解法2从点P的坐标出发，由切线PA,PB的统一形式，2次利用韦达定理，根据重心坐标公式求出重心轨迹方程.

2)解法1 问题1的改进中已给出(略).

解法2 对点P的位置进行讨论:当xP=0，即P(0,-2)时，由对称性显然∠PFA=∠PFB；当xP≠0时，显然∠PFA与∠PFB不互补，从而

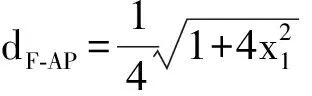
由等面积变形:一方面,

另一方面,

从而

于是

∠PFA=∠PFB.

综上所述，∠PFA=∠PFB.

分析 解法1根据∠PFA=∠PFB⟺cos∠PFA=cos∠PFB，巧妙地引进向量数量积的运算，进行合理转化，从而完成证明；解法2进行分类讨论，在∠PFA与∠PFB不互补的前提下，利用三角形等面积变形，证明了sin∠PFA=sin∠PFB，从而得出∠PFA=∠PFB.

问题3 背景挖掘不深刻.

题目的背景是解题者思路的来源.若不能准确把握题目的背景，则题目的重点不突出，讲题的效率较低.

教师2这样阐述题目背景：本题是以抛物线为背景的圆锥曲线综合试题，涉及重心、轨迹方程等多种知识，综合难度较大！

反思 在说题目背景时，不能仅停留在题目表面，需对题目的某个角度有一个较深刻的认识：可以说题目的内涵，也可以说题目可由某个试题演化而来.若教师能准确说出题目的内涵或来源，则说明该教师功底深厚.

问题4 研究变式太肤浅.

在比赛过程中，个别教师在说题目变化时说得比较少，或者不会变化.如教师3将原题中点P的坐标改为(1,-1)，第1)小题改为求△APB的重心G的坐标，第2)小题不变.

反思 教师3将题中动点改为定点，不但没变好，反而降低了题目的品味.真正的变式研究需有一定的深度，不能仅停留在数据的更改、字母的变更等较为肤浅的变化上，最好能通过适当的变形，让题目的解法有一个较大的变化或在解法过程中产生一些闪光点.

改进 结合题目极点、极线知识背景进行适当改编，得出以下2个变式.

变式1 如图2,A,B为抛物线C：y=x2上的2个点，线段AB过抛物线C的焦点F，分别以A,B为切点作2条切线PA,PB相交于点P，求△APB重心G的轨迹方程.

图2 图3

问题5 功能展开太宽泛.

说题时，一个很重要的方面是要说说题目的价值，即我们常说的题目功能.题目的功能有很多种，如教学功能、检测功能、练习功能等.

反思 笔者认为结合比赛的场合、时间等因素，在说题目的功能时，不必面面俱到，面面俱到反而给人以“啰嗦、没重点”的感觉，只需着重针对题目的某个功能，进行简单明了地叙述即可.

改进 题目分很多种，有些题适合作为考题，有些题适合作为例题，有些题则适合作为练习题.本题为高考真题，其检测功能不言而喻，而今作为高三复习课的一个例题进行教学:第1)小题的解法1，提醒学生求抛物线切线的一种新方法——利用导数；解法2提醒学生过曲线外一点作曲线的切线，可利用2条切线的统一形式(同2011年浙江省数学高考理科第21题)；第2)小题的2种解法分别从向量数量积和三角形等面积变形出发，通过证明2个角的三角函数值相等从而得出这2个角相等.以上解法中涉及重心、切线、轨迹、导数、距离、面积、向量等多方面知识，综合性很强，有较高的教学价值.

说题比赛对加强教师间的业务交流、提高教师的基本技能、推进学校的教学质量等都有显著的促进作用.说题是一项优质的教师教研活动.