基于宏程序的数控插补原理实验教学研究
李慧玲 罗敏


【摘要】对传统数控插补原理教学过程中以课堂讲授为主结合VC、VB等编程语言完成插补过程仿真的教学方法进行改革,创新性地采取让学生亲自动手在实际的FANUC-0i-mate-C数控加工中心综合实验台上,采用调用用户宏程序的方法,用画笔在平铺于工作台面上的白纸上模拟绘制逐点比较法插补或数字积分法插补的过程的教学方式,使插补原理及宏程序编程两部分重要理论密切联系,并与实践紧密结合。
【关键词】插补原理 数控 宏程序
【中图分类号】G71 【文献标识码】A 【文章编号】2095-3089(2015)05-0037-03
一、引言
传统数控插补原理教学,大多以课堂讲授为主,结合VC、VB等各种编程语言完成插补过程的仿真。这种教学方法不能将理论知识与现有实验教学设备有机结合,学生普遍反映内容抽象,理解困难,与实践脱节。
为了改革传统数控插补原理教学过程中教师灌输过多,学生参与过少;理论性结论过多,启发式问题过少的教学方式,有针对性地创新教学方法:要求学生在实际的FANUC-0i-mate-C数控加工中心综合实验台上,采用调用用户宏程序的方法,用画笔在平铺于工作台面上的白纸上模拟绘制逐点比较法插补或数字积分法插补的过程。这样就将一个对插补原理进行仿真的演示性实验改造成了理论上综合了插补原理及宏程序编程两部分重要内容,实践上锻炼了学生对实际数控系统的操作及调试能力的综合性实验。
二、插补原理
在数控机床实际加工中,数控系统根据输入的零件程序的信息,按照某种算法将程序段所描述的曲线的起点、终点之间的空间进行数据密化,从而形成刀具加工轨迹,这种“数据密化”机能就称为“插补”。按照插补运算所采用的基本原理和方法,数控系统的插补原理通常可归纳为脉冲增量插补和数据采样插补两大类。
逐点比较法是脉冲增量插补中最典型的算法,原理是:在控制过程中,逐点计算和判断运动轨迹与给定轨迹的偏差,并根据偏差控制进给轴向给定轮廓靠近,缩小偏差,使加工轮廓逼近给定轮廓。以折线来逼近直线或圆弧,最大误差不超过一个脉冲当量。
以第一象限逆圆为例:圆弧(AB) ,其圆心在坐标原点,已知起点为A(X_A,Y_A ),终点为B(X_B,Y_B ),圆弧半径为R,瞬时加工点P(X_i,Y_i )与圆心的距离为R_i。取F_i=R_i^2-R^2=X_i^2+Y_i^2-R^2为偏差判别式,若P点在圆弧上或在圆弧外,即F_i≥0时,为了使加工点逼近圆弧,应向-X方向进给一步。进给后的新坐标值为:X_(i+1)=X_i-1;Y_(i+1)=Y_i,则新的偏差为:F_(i+1)=R_(i+1)^2-R^2=X_(i+1)^2+Y_(i+1)^2-R^2=(X_i-1)^2+Y_i^2-R^2=F_i-2X_i+1;若P点在圆弧内,即F_i<0时,应向+Y方向进给一步。进给后的新坐标值为:X_(i+1)=X_i;Y_(i+1)=Y_i+1,新的偏差为:F_(i+1)=R_(i+1)^2-R^2=X_(i+1)^2+Y_(i+1)^2-R^2=X_i^2+(Y_i+1)^2-R^2=F_i+2Y_i+1。同时设置一终点计数器,其初值为∑·〖=|X_B-X_A | 〗+|Y_B-Y_A |,即从起点到终点的总步数,X或Y坐标每进给一步,∑减去1,直到∑=0时,到达终点。故逐点比较法圆弧插补计算过程的每一步分为五拍:偏差判别、坐标进给、偏差计算、坐标计算及终点判别。圆弧的象限及顺逆不同,则插补计算公式和进给方向也不同,四个象限的圆弧插补偏差计算公式和进给方向见表1。若圆弧存在过象限的问题,可将圆弧按象限分段处理。
表1 四象限圆弧插补的偏差计算公式及进给方向
Fi≥0 Fi<0
圆弧所在象限及方向 进给方向 偏差计算 坐标计算 圆弧所在象限及方向 进给方向 偏差计算 坐标计算
Ⅰ顺、Ⅱ逆 -Y Fi+1=Fi-2|Yi |+1 |Xi+1|=|Xi |
|Yi+1|=|Yi |-1 Ⅰ顺、Ⅳ逆 +X Fi+1=Fi+2|Xi|+1 |Xi+1|=|Xi|+1
|Yi+1|=|Yi|
Ⅲ顺、Ⅳ逆 +Y Ⅲ顺、Ⅱ逆 -X
Ⅳ顺、Ⅰ逆 -X Fi+1=Fi-2|Xi |+1 |Xi+1|=|Xi|-1
|Yi+1|=|Yi | Ⅱ顺、Ⅰ逆 +Y Fi+1=Fi+2|Yi|+1 |Xi+1|=|Xi|
|Yi+1|=|Yi|+1
Ⅱ顺、Ⅲ逆 +X Ⅳ顺、Ⅲ逆 -Y
三、FANUC宏程序
用户宏程序是像子程序一样,在存储器中存储一组指令的功能,存储的这组指令功能用一条指令表示或调用执行。这一组指令称为用户宏程序本体,简称宏程序;把代表指令称为用户宏程序调用指令,简称宏指令。FANUC宏程序具有许多可在计算机高级语言中发现的特征:算术和代数计算;三角法计算;变量数据存储;逻辑运算;分支;循环;错误检查;报警产生;输入和输出。
因此,可以利用FANUC宏程序的这些特点进行逐点比较法插补模拟程序的模块化:例如,在主程序中仅完成起点与终点坐标的赋值及坐标轴的绘制,而将包括偏差判别、坐标进给、偏差计算、坐标计算及终点判别的整个插补过程在宏程序中完成。这样,只需在主程序中改变起点及终点坐标,而无需对宏程序进行任何变动,即可完成所需的插补过程模拟。同时,在宏程序中,利用条件转移指令实现偏差判别后确定进给轴及进给方向的分支功能;利用循环指令或条件转移指令实现终点判别及终点未到之前,偏差判别、坐标进给、偏差计算、坐标计算及终点判别这五拍的迭代进行,使宏程序编程得到简化。
通常宏程序由主程序或其他的宏程序使用G代码(典型的是G65)调用。
宏指令的基本格式为:G65 P L <自变量>;其中G65为宏程序调用命令;P 为包含宏程序的程序号。L 程序循环次数(L1为默认值);自变量为传递给宏程序的局部变量的定义。
四、基于宏程序的逐点比较法第三象限逆圆插补的实现
这里仅以逐点比较法第三象限逆圆插补(圆心在坐标原点)为例,介绍使用调用宏程序完成插补模拟的过程。
首先,在主程序中完成圆弧起点及终点坐标的赋值、坐标轴的绘制,宏程序的调用包括表示圆弧起点及终点坐标的局部变量的赋值。
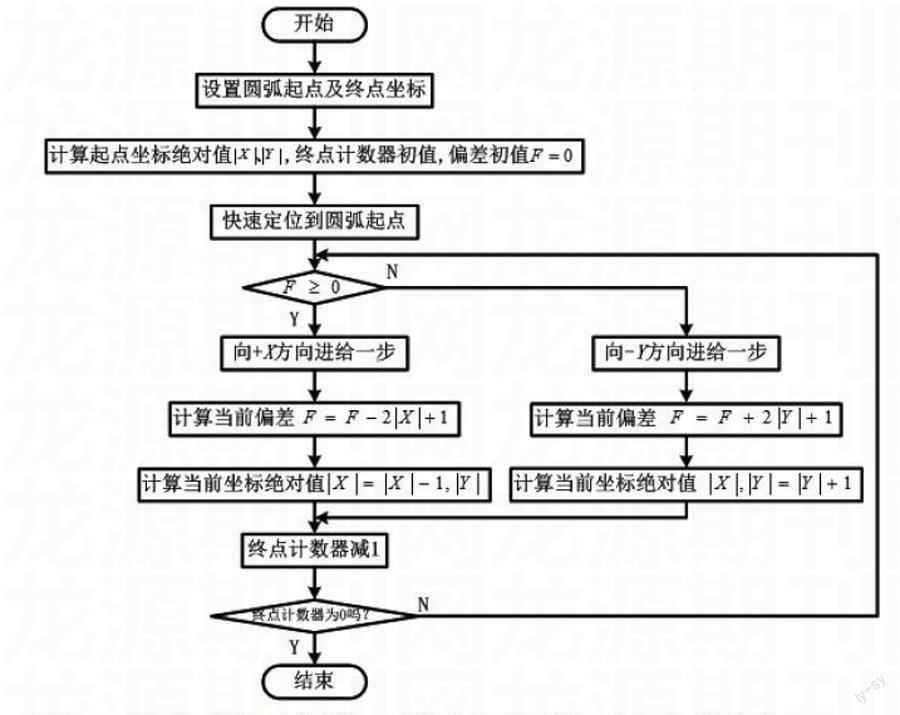
在用户宏程序中完成圆弧起点的快速定位,圆弧插补的偏差判别、坐标进给、偏差计算、坐标计算及终点判别等全部插补过程。在这里特别要注意的是:为了清楚地绘制插补过程,需要将各轴的脉冲当量进行适当放大。逐点比较法第三象限逆圆插补流程图如图1所示。
图1 逐点比较法第三象限逆圆插补流程图
宏调用格式G65 P8011 X Y A B F ;
有关自变量定义如下
X(#24):圆弧起点X轴坐标X
Y(#25):圆弧起点Y轴坐标Y
A(#1):圆弧终点X轴坐标A
B(#2):圆弧终点Y轴坐标B
F(#9):切削进给速度F
主程序:
O1234;
N60 G90 G54 G00 X0 Y-60;采用工件坐标系绝对模式
N70 G01 Y0 F100;绘制Y坐标轴
N80 X-60;绘制X坐标轴
N90 G65 P8011 X-5 Y0 A0 B-5 F100;调用用户宏程序O8011
N100 G00 X0 Y0;回坐标原点
N110 M30;主程序结束
宏程序
O8011;
N200 #33=#4003;保存编程模式
N210 #3=ABS[#24];圆弧起点X轴坐标绝对值|X|
N220 #4=ABS[#25];圆弧起点Y轴坐标绝对值|Y|
N230 #5=ABS[#1-#24]+ABS[#2-#25];终点计数器初值,#24=#500,#25=#501,#1=#502,#2=#503
N240 #6=0;设置插补计算偏差初值F=0
N250 G00 X[10*#24] Y[10*#25];定位圆弧起点,并将坐标值放大10倍
N260 G03 X[10*#1] Y[10*#2] R[SQRT[#24*#24+#25*#25]*10] F#9;绘制参考圆弧
N270 G00 X[10*#24] Y[10*#25];再次回到圆弧起点
N280 IF [#6 GE 0] GOTO 310;如果偏差大于等于0,转移到N330
N290 G91 G01 Y-10 F#9;当偏差小于0时,向-Y方向进给一步(10mm)
N300 #6=#6+2*#4+1;计算当前偏差 F=F+2|Y|+1
N310 #4=#4+1;计算当前坐标的绝对值 |Y|=|Y|+1
N320 GOTO 360
N330 G91 G01 X10 F#9;向+X方向进给一步(10mm)
N340 #6=#6-2*#3+1;计算当前偏差 F=F-2|X|+1
N350 #3=#3-1;计算当前坐标的绝对值 |X|=|X|-1
N360 #5=#5-1;终点计数器减1
N370 IF[#5 NE 0] GOTO 280;若终点计数器不为0,转移到N280继续进行圆弧插补
N380 G#33;恢复编程模式
N390 M99;宏程序结束
FANUC-0i-mate-C数控加工中心综合实验台如图2所示。运行结果如图3所示。
图2 FANUC-0i-mate-C数控加工中心综合实验台 图3 逐点比较法第三象限逆圆插补轨迹
逐点比较法第三象限逆圆插补理论计算过程如表2。
表2 逐点比较法第三象限逆圆插补理论计算过程
步数 偏差判别 坐标进给 偏差计算 坐标绝对值计算 终点判别
0 F0=0 |X0|=5;|Y0 |=0 ∑= 5+5=10
1 F0=0 +X F1=F0-2|X0|+1=-9 |X1|=4;|Y1|=0 ∑= 10-1=9
2 F1<0 -Y F2=F1+2|Y1|+1=-8 |X2|=4;|Y2|=1 ∑= 9-1=8
3 F2<0 -Y F3=F2+2|Y2|+1=-5 |X3|=4;|Y3|=2 ∑= 8-1=7
4 F3<0 -Y F4=F3+2|Y3|+1=0 |X4|=4;|Y4|=3 ∑= 7-1=6
5 F4=0 +X F5=F4-2|X4|+1=-7 |X5|=3;|Y5|=3 ∑= 6-1=5
6 F5<0 -Y F6=F5+2|Y5|+1=0 |X6|=3;|Y6|=4 ∑= 5-1=4
7 F6=0 +X F7=F6-2|X6|+1=-5 |X7|=2;|Y7|=4 ∑= 4-1=3
8 F7<0 -Y F8=F7+2|Y7|+1=4 |X8|=2;|Y8|=5 ∑= 3-1=2
9 F8>0 +X F9=F8-2|X8|+1=1 |X9|=1;|Y9|=5 ∑= 2-1=1
10 F9>0 +X F10=F9-2|X9|+1=0 |X10|=0;|Y10|=5 ∑= 1-1=0
实际运行结果与理论计算完全相符。
五、结论
学生通过用户宏程序编程,了解了宏变量和宏指令的应用,掌握了用户宏程序的编程、输入、编辑、调试及调用的方法;并通过数控插补原理实验,进一步理解并掌握了逐点比较插补原理和数字积分插补原理。故基于宏程序的插补原理实验教学方法改革真正做到了以问题为主线,以综合实践为导向,引导学生掌握科学的学习方式,让学生主动参与、乐于钻研、勤于动手,极大地提高了学生的学习能力和教学效果。
参考文献:
[1]罗敏等.数控原理与编程[M].北京:机械工业出版社,2011.
[2]罗敏.FANUC数控系统设计及应用[M].北京:机械工业出版社,2014.

