高速公路铣刨机驱动转向桥有限元分析与优化*

陈道攀，潘晓东，李剑敏，宣海枫，王 威，周新腾

(1.浙江理工大学浙江省机电产品可靠性技术研究重点实验室，浙江杭州 310018;2.杭州前进齿轮箱集团股份有限公司，浙江杭州 311203)

0 引言

20世纪80年代后，随着我国改革开放进程所带来的交通流量的大幅度增加，我国开始了高速公路的大规模建设［1］。到目前早期建设的高速公路已经服役近20多年，且国内公路上车流密度较大，重载货车超载情况普遍，导致高速公路路面损害严重，修补工作极其繁重。高速公路路面修补需要把破洞部分扩开、铲平、清洁，然后进行适当的修补［2－3］，整个过程费时费力，且对公路的交通影响较大。近年来，公路管理者引入了高速公路专用的大型铣刨机来完成公路修补的主要工序，极大地提高了维修作业和交通通行效率，满足了高速公路快速维修的需要［4］。但高速公路铣刨机引入我国的时间不长，消化吸收不充分，对一些关键总成的结构没有深入的研究。而铣刨机与装载机、挖掘机等同为工程机械［5］，但其服役工况完全不同，且铣刨机一般采用转向桥，具有独特的操作工况，如长时间地慢速前进，频繁地转向，负荷不太大等等。笔者对某铣刨机转向桥进行了分析与优化，优化结果减小了截面尺寸，减轻了重量，同时结构满足驱动桥的强度、刚度标准。

1 转向桥模型

笔者研究铣刨机驱动桥在工作中具有转向，驱动和制动功能，在结构上采用了横置一体式液压油缸和湿式制动摩擦片等国际先进技术，是目前国内较为先进的工程机械转向桥。其主要结构如图1所示。图2为建立的三维数值模型图。该铣刨机转向驱动桥为铸造桥壳，材料为球墨铸铁QT450－10，有较好的韧性和塑性，常温状态下其材料的力学性能如表1。

图1 转向桥结构示意图

图2 转向桥数值模型

表1 QT450－10球墨铸铁的力学性能

有限元分析的实质是以各单元在受力下的近似平衡结果之和来代替结构的整体平衡结果，因此，单元划分的好坏对分析结果有较大的影响。一般结构分析中，采用的判断标准是当单元尺寸更加划小时，分析结果趋于一稳定值。笔者考虑到转向桥的实际尺寸，以及网格划分的经济性和计算结果的准确性，分别设定网格尺寸为20 mm、15 mm、10 mm、7.5 mm、5 mm进行网格划分，并进行额定载荷的计算。计算结果如表2，随着网格尺寸的减小，桥的总体变形基本不变，但应力情况有着明显的变化。表明在有限元计算中，变形(位移)作为直接变量，受单元等影响较小;而应力作为变形(位移)的导数，其计算精度要比变形差，对单元尺寸等因素比较敏感。当网格尺寸减小至7.5 mm时，最大应力较10 mm时急剧减小，但继续减小网格尺寸时，最大应力基本保持不变，无明显变化。考虑到准确性和经济性要求，采用7.5 mm的单元尺寸进行网格划分，对应力危险区域进行局部网格细化。采用AYSYS的三维实体单元SOLID45，该单元为线性三维单元，具有较好的边界模拟能力，整个转向桥划分为1 207 967个单元、含1 863 729个节点，建立的局部有限元网格模型如图3所示。

图3 转向桥有限元模型－局部

表2 不同尺寸单元模型计算结果对照

2 有限元分析与优化

按照驱动桥原型设计［6－7］，铣刨机两个转向包左右端面之间的距离为1 438.80 mm，整机操作工况总载荷为为137 200 N。工程机械一般前桥负荷约为总负荷的3/5，即82 320 N，计算取前桥承受的总载荷为90 000 N。轴荷加载在摇摆架上，摇摆架安装于桥壳主箱体的前后轴承轴上。

铣刨机转向桥连接在车身上，讨论其受基本垂向载荷，则其约束条件可简化为:对左、右轴承处施加约束，以限制转向桥的移动;在摇摆架上施加均布载荷，其大小等于桥的总载荷除以摇摆架面积。通过ANSYS计算，得到桥壳变形与应力分布云图，如图4、5。

图4 驱动桥额定载荷－变形云图

图5 驱动桥额定载荷－应力云图

经计算得额定载荷下桥壳的最大位移为0.615 mm，与轮距之比为0.43 mm/m。按照工程机械行业标准，即满载轴荷时桥壳每米轮距的最大变形不超过1.5 mm。计算结果表明，桥的垂向变形不仅小于行业标准要求，且有很大余量，转向桥的刚度足够。桥壳的最大应力为112.5 MPa，也远小于QT450材料的屈服极限，因此，该转向桥存在较大的结构优化余地。桥壳最大应力部位为桥壳与万向节连接半球面处、轴端与桥壳连接的轴肩处，这两处位置由于接触以及结构突变等原因，易产生应力集中，是整个转向桥的危险截面。

对于优化问题，通常可用数学模型表示为:

式中:x，v为分别是状态变量和设计变量;g1，g2为对设计变量和状态变量的约束方程;f(x，v)为设计变量的目标函数，通常优化为求该目标函数的极小值。

笔者对转向桥的计算分析表明，该桥在额定桥荷作用下的最大应力与变形都比较小，具有较大的强度、刚度裕度，因此，可以通过优化设计，以提高转向桥材料利用率，减轻桥的重量。在转向桥优化中，注意到转向桥的主要几何参数中，桥长度受到铣刨机的轮距等联接条件限制而无法自主设计，因此，选取了桥的横截面(宽度、高度)、摇摆箱长度等几何尺寸作为优化的设计变量，其约束变量仍然满足最大单位轮距变形不大于1.5 mm，以及最大应力＜材料屈服应力。优化的目标函数为桥的总体积(质量)最小。其中具体的状态变量与设计变量列于表3。

表3 驱动桥优化设计变量、状态变量及约束条件

从优化前后的结果看，经过优化分析后，转向桥的截面尺寸有所减小，桥壳截面宽和高分别从150 mm、120 mm减小到135 mm、105 mm，摇摆箱直径从115 mm减小到105 mm。经过截面减小后的转向桥，其在额定桥荷下的最大变形和单位长度变形分别从0.615 mm 和0.43 mm 增加到0.64 mm 和 0.45 mm，仍然远小于行业标准。但经优化后的最大应力，从112.5 MPa增加到133.1 MPa，虽然仍然小于企业期望的190 MPa，但其与标准的差距不如变形那么大。

通过桥壳尺寸的优化，减小了桥壳的体积，减轻了桥的重量，节约了桥的材料，且在载荷作用下桥的变形与应力均发生了少量的增加，满足行业标准和企业要求，达到了转向桥优化目的。

图6 优化后的驱动桥应力云图

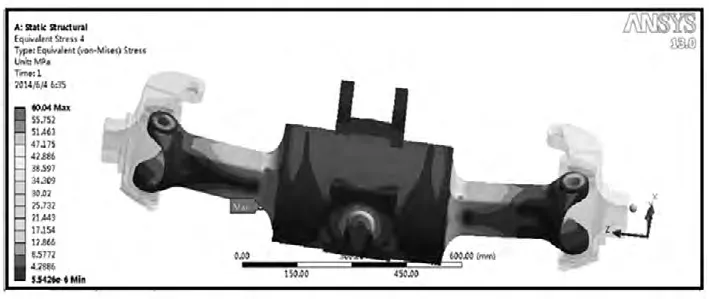
图7 转向工况驱动桥应力云图

3 驱动桥典型工况有限元分析

铣刨机工作时，除了在公路破洞处缓慢移动进行修补操作外，也要在高速公路上进行快速运动以到达公路破损处。对驱动桥而言，就存在着高速前进、紧急制动、满载慢速等典型工况［8］，而其中，紧急制动由于产生较大的负加速度(惯性力)而成为危险工况。另外，铣刨机驱动桥为转向桥，其转向是通过驱动桥两端的两只转向油缸拉动转向杆实现的。因此，笔者选取了紧急制动和转向两个典型工况对驱动桥进行计算。

铣刨机转向行驶时，转向桥一侧受转向油缸拉力作用，发生偏转，从而带动车轮及铣刨机发生转向。此时，转向桥受到特殊外力主要是转向油缸的拉力以及转动所产生的离心力。相对而言，由于转向角速度不大，离心力也较小。该型铣刨机的最小转弯半径r=5.97 m，最大行驶速度按 v=20 km/h=5.6 m/s，则铣刨机转向的最大离心力为7 354 N;转向油缸的油压为14 MPa，油缸内径为38 mm，因此，转向油缸的拉力为16 981.5 N。以此载荷作为工况条件，对转向桥壳进行有限元分析，得到桥壳最大变形为0.45 mm，变形量很小。其应力分布如图7所示，桥壳的最大应力为60.04 MPa，应力分布较为平均。由此表明在转向工况下，桥壳处于较低的应力范围内工作，结构安全。

紧急制动是运动车辆(包括汽车、工程机械等)的危险工况。铣刨机制动时，制动力(力矩)计算可以从发动机的制动功率计算，也可以从地面附着力计算。但最终提供制动力的是地面附着力(摩擦力)，因此，笔者根据车轮的地面附着力计算制动力。当紧急制动时，地面提供附着力为:

式中:φ为路面附着系数，由于铣刨机常在破损路面工作，地面比较粗糙，地面附着系数较大，作为极限工况考虑，取φ=0.9，从而计算得最大制动力为123 480 N。

当铣刨机处于紧急制动工况时，由于制动力的作用，导致车辆头部下沉，在前桥受到额外的作用力。该力可以通过车辆的力矩平衡计算得到:

式中:FCX为地面对前桥的垂向反作用力;H为重心高度;L为前后桥之间的距离;Lz为铣刨机重心与后桥的距离，计算可得垂向力FCX为135 828 N。

以紧急制动工况载荷进行有限元分析，桥壳变形如图8所示，桥壳最大变形为1.12 mm，单位轮距的变形为0.78 mm，小于行业标准要求。桥壳应力分布如图9所示，桥壳最大应力为381.92 MPa，发生在桥壳与活塞缸体连接过度区域的圆角处，主要为该处结构上的应力集中引起。总的桥壳应力小于材料强度极限，但大于材料的屈服极限，但大于屈服极限的区域较小，仅限于过渡倒角的局部范围内。该结果表明结构处于局部塑形状态，但塑形区域很小，且该塑形是由于局部应力集中引起，不会导致塑形区域的大范围扩张，总体上结构还是安全的。但由于应力已经超出屈服极限，因此，对结构将造成一定的损伤，并累积起来可造成结构的疲劳裂纹导致破坏。而紧急制动本身是危险工况，一般仅在紧急避险时采取该动作，因此，在桥壳的服役期间，紧急制动工况并不频繁发生，因而能够保证驱动桥的使用寿命。

4 结论

采用有限元方法，对某铣刨机转向驱动桥进行了分析与优化，主要结论如下:

(1)建立了转向桥的数值模型，在原型桥计算分析的基础上，提出了优化设计方案，对桥的几何尺寸进行了削减，减轻了桥的重量。

(2)额定桥荷、转向、紧急制动等典型工况载荷下的有限元分析结果，表明经过优化后的转向驱动桥具有较好的强度和刚度，能够满足企业要求，也验证了优化的有效性。

(3)紧急制动为转向驱动桥的最危险工况，其应力虽小于材料的强度极限，但安全系数不大，且已经超过屈服极限，因此，频繁的紧急制动将对结构造成损失，降低其寿命。铣刨机在操作中应尽量避免紧急制动。

(4)铣刨机转弯时，转向油缸的拉力作用于驱动桥上，所形成的应力较小，对驱动桥的安全与寿命不会发生影响。

［1］ 张 玢.河北省高速公路与区域经济协调发展研究［D］.石家庄:石家庄铁道大学，2012.

［2］ 刘 亚.铣刨机路面铣削过程的有限元仿真［D］.湘潭:湘潭大学，2009.

［3］ 王 震.铣刨机铣削过程动力学仿真及实验研究［D］.湘潭:湘潭大学，2013.

［4］ 游张平，李自光，邓习树，等.路面铣刨机及其发展趋势［J］.建筑机械化，2003(9):9－12.

［5］ 项生田.装载机驱动桥壳疲劳寿命预测研究［D］.杭州:浙江理工大学，2011.

［6］ M.M.Topac，H.Gunal，N.S.Kuralay.Fatigue Failure Prediction of a Rear Axle Housing Prototype by Using Finite Element Analysis［J］.Engineering Failure Analysis.2009(16):1474 －1482

［7］ 申守平.转向驱动桥壳的受力与台架试验［J］.现代零部件，2010(10):41－42.

［8］ 郑燕萍，羊 玢，王顺宏.驱动桥壳典型工况的有限元设计［J］.林业机械与木工设备，2004，32(8):25－26.