道岔侧板变形装置关键部件的疲劳寿命分析*

代春香，林腾蛟，吕和生

(1.四川大学锦城学院机械工程系，四川成都 611731;2.重庆大学机械传动国家重点实验室，重庆 400044;3.重庆齿轮箱有限责任公司，重庆 402263)

0 引言

疲劳破坏是工程结构和机械失效的主要原因之一，引起疲劳失效的循环载荷峰值往往远小于静态断裂分析估算的安全载荷［1］，因此，为了提高结构可靠性，对其关键部件开展疲劳研究有着重要意义。

道岔侧板变形装置的结构设计理念中，要求结构尽可能轻量化，高度的可靠性和足够的寿命，而侧板变形装置工作时会承受外部载荷循环动载荷，在这种循环动载荷的作用下，装置的许多构件都会产生动态应力，从而引起疲劳损伤［2］，而损伤累积后的结构破坏的形式经常是疲劳裂纹的萌生和最终结构的断裂破坏。因此，需进行道岔侧板变形装置的疲劳分析。

1 疲劳寿命计算方法

名义应力疲劳分析法以名义应力为基本设计参数，以S－N曲线为主要设计依据的抗疲劳设计法。名义应力法表示外加应力水平和标准试样疲劳寿命之间关系的曲线，该曲线通常都是表示中值疲劳寿命与外加应力间的关系，所以也称中值S－N曲线［3］。S－N曲线是由标准试件在疲劳试验机上试验得到的，用一组标准试件，在一定平均应力σm(或一定的循环特征R)下，施加不同的应力幅，测出试件断裂时的循环数N。然后以σmax为纵坐标，N为横坐标，画点并连接可得相应于该 σm(或 R)下的 S－N曲线［4］。

结构疲劳设计中主要的两方面是:制成构件的材料的疲劳寿命曲线;构件的工作载荷谱。计算疲劳的步骤包括材料数据、载荷历程以及几何原型的输入，最后得出结构的疲劳寿命。

FE－SAFE疲劳分析流程为:

(1)获得载荷谱 FE－SAFE中疲劳载荷谱是由有限元静力解和载荷历程构成。

(2)定义材料属性 可利用材料的抗拉强度(UTS)和弹性模量(E)生成近似的材料数据，因疲劳计算考虑存活率要求、材料安全系数、检测因素等影响，须对S－N曲线进行修正［5］。

(3)疲劳寿命求解计算及在ANSYS中查看其疲劳寿命和安全系数。

疲劳寿命:道岔侧板变形装置的设计使用寿命为50年，若构件的计算疲劳寿命达到或超过其设计寿命，则其疲劳寿命满足要求。

疲劳安全系数:若将疲劳载荷同时放大n倍，构件的疲劳寿命刚好等于设计寿命，则n称为构件的疲劳安全系数［6］。若疲劳安全系数达到或超过1.0，则认为构件有足够的疲劳安全系数。

笔者采用ANSYS软件，建立道岔装置侧板的静力有限元模型和凸轮组的接触有限元模型，计算静载荷下侧板和凸轮组的等效应力。在FE－SAFE软件中，建立侧板构件材料和凸轮组各构件材料的修正S－N曲线，将ANSYS静力有限元分析结果与已知的载荷－时间历程相结合，采用名义应力法，计算侧板和凸轮组的疲劳寿命。

2 侧板疲劳寿命分析

2.1 有限元静力分析

采用8节点六面体单元对侧板实体模型进行有限元网格离散化处理，并在其支耳的内孔中心轴处建立刚性区域，以便在此处施加载荷，侧板的材料参数见表1。图1给出了侧板的有限元计算模型，共计单元数32457，节点数48528。

侧板施加的边界条件如下:

(1)节点48521的X、Y、Z向移动自由度以及绕X、Y轴的转动自由度。

(2)中间6个节点48522～48527的Z向移动自由度以及绕X、Y轴转动自由度。

(3)节点48528的Y、Z向移动自由度以及X、Y轴的转动自由度。

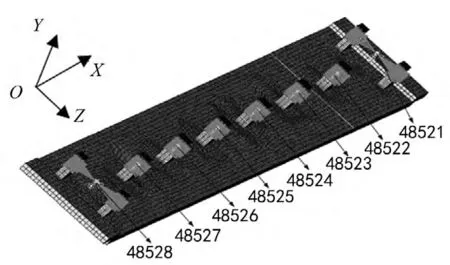
图1 侧板的有限元计算模型

采用的单位载荷进行有限元静力计算，即在8个刚性区域节点各施加 FX、FY、FZ、MX、MY、MZ六个单位载荷并进行静力计算，从而得到各单位载荷下的应力结果共48个。图2给出了部分应力结果，以a代表48 524节点，b代表48 525节点。

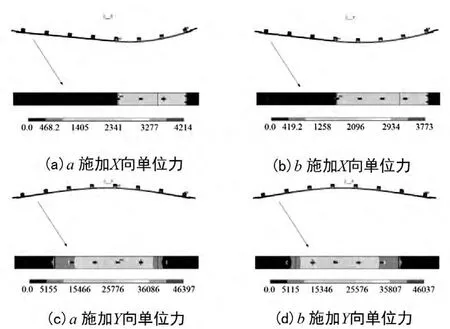
图2 单位载荷下侧板的等效应力云图

2.2 侧板的S－N曲线

S－N曲线定义为在循环应力中给定应力比或平均应力时，构件材料的疲劳寿命N与应力幅值S的关系曲线［7］。侧板材料修正S－N曲线的相关参数如表1所列。

表1 侧板材料修正S－N曲线的相关参数

在Matlab中编写程序，确定构件材料S－N曲线上的三个转折点(n1，sigema1)，(n2，sigema2)，(n3，sigema3)的位置。侧板材料的修正S－N曲线计算程序如下:

format long

sigemab=375

sigemas=225

t=30

alphak=1.55

n=0.75

Ft=1

gammaM=1.15

Fo=1 － 0.22*((log10(1.6))^0.64)*log10(sigemab)+0.45*(log10(1.6))^0.53

Fot=1－sqrt((1－Fo)^2+(1－Ft)^2)

betak=alphak/n

Fotk=sqrt(betak^2－1+1/Fot^2)

sigemaw=0.436*sigemas+77

M=0.00035*sigemab －0.1

m1=12.0/Fotk^2+3

m2=2*m1－1

d=6.4 －2.5/m1

ND=10^(6.4 －2.5/m1)

sigemawk=sigemaw/Fotk

u=1/(1+M)*sigemawk/sigemab

a=sigemawk/sigemab

p=(1/(1+M)－1+u^2)/(u^2－u)

if p＞1

Fm= －1*(1+p*a)/(2*a^2*(1－p))－sqrt(1/((1－p)*a^2)+((1+p*a)/(2*a^2*(1－p)))^2)

elseif p＜=1

Fm= －1*(1+p*a)/(2*a^2*(1－p))+sqrt(1/((1－p)*a^2)+((1+p*a)/(2*a^2*(1－p)))^2)

end

sigemaA=sigemawk*Fm

S=2/3*((t/25)^－0.1)

deltasigemaA=2*sigemaA*S/gammaM

deltasigema1=sigemas*(1－R)/gammaM

n1=ND*(deltasigemaA/deltasigema1)^m1

sigema1=deltasigema1

n2=ND

sigema2=deltasigemaA

n3=10^9

sigema3=deltasigemaA/((n3/ND)^(1/m2))其中:sigemab(σb)为抗拉强度;sigemas(σs)为屈服强度;t为材料厚度;alphak(αk)为集中应力参数;n为缺口敏感系数;gammaM(γm)为局部安全系数。

计算得三个转折点分别为(12725.9，196)、(930232.8，90)、(109，48)，在 FE － SAFE 中生成侧板材料的修正S－N曲线，如图3所示。

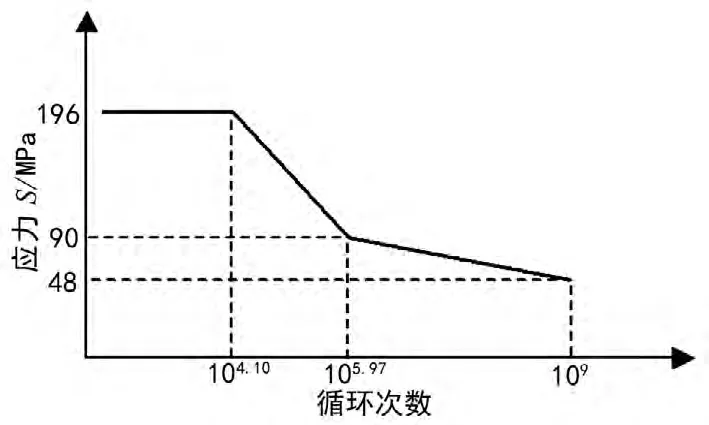
图3 侧板材料的修正S－N曲线

2.3 疲劳寿命计算

在疲劳分析软件FE－SAFE中，读入侧板的有限元分析结果，设置变量单位后可生成一个应力集。有限元分析时采用的单位载荷，因此调入侧板已知的载荷历程文件作为疲劳寿命分析时的载荷谱，侧板载荷谱有相应的48个工况。将单一工况的载荷历程分别与应力集相结合，生成疲劳载荷块，疲劳载荷文件如下:

# .ldf file created by fe－safe 5.4 －03［mswin］

INIT

transitions=Yes

END

#Block number 1

BLOCK n=67160，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=2，ds=1，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=3，ds=2，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=4，ds=3，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=5，ds=4，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=6，ds=5，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=7，ds=6，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=8，ds=7，scale=1

lh=E:DaoChaCeBan xtfx.txt，signum=9，ds=8，scale=1

lh=E:DaoChaCeBan xtfy.txt，signum=2，ds=9，scale=1

lh=E:DaoChaCeBan xtfy.txt，signum=3，ds=10，scale=1

┇

lh=E:DaoChaCeBan xtmy.txt，signum=8，ds=39，scale=1

lh=E:DaoChaCeBan xtmy.txt，signum=9，ds=40，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=2，ds=41，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=3，ds=42，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=4，ds=43，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=5，ds=44，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=6，ds=45，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=7，ds=46，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=8，ds=47，scale=1

lh=E:DaoChaCeBan xtmz.txt，signum=9，ds=48，scale=1

END

上述疲劳载荷谱定义以1年为单位，因此侧板疲劳寿命分析时，设计寿命设置为50次循环，即为50年。采用Goodman平均应力准则修正后的最大主应力－疲劳寿命算法，对侧板进行疲劳寿命分析。

图4和图5分别给出了侧板的对数疲劳寿命和安全系数，其值为常用对数表示的循环次数。由图4可知，侧板的疲劳寿命对数值最小为1.857，出现在自右往左第四个支耳的根部，疲劳寿命以年表示为Nlife=101.857=71.94年。疲劳安全系数达到或超过1.0，则认为侧板有足够的疲劳安全系数，即满足设计要求。图5给出了侧板在50年设计寿命条件下的疲劳安全系数分布云图，侧板的疲劳安全系数最小值为1.031，位置出现在的第四个支耳的根部，与疲劳寿命最小位置相同。可见，虽然以时间表示侧板的疲劳寿命达到了71.94年，但是其疲劳安全系数并不大。

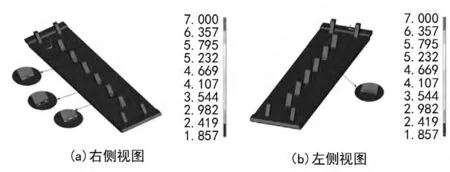
图4 侧板的对数疲劳寿命

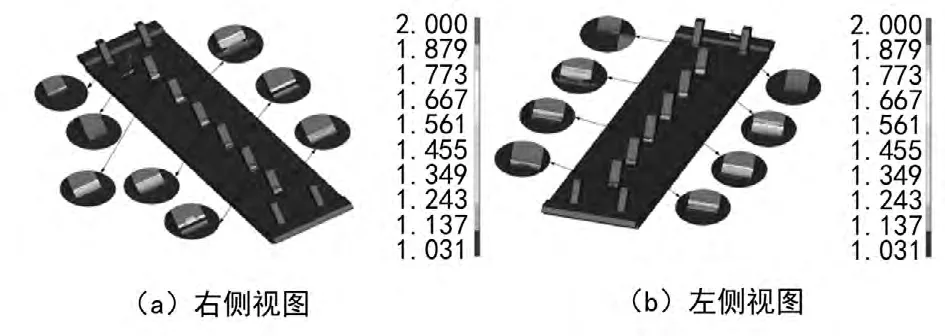
图5 侧板的疲劳安全系数

3 凸轮组疲劳寿命分析

3.1 有限元静力分析

由道岔侧板变形装置动力学仿真得出凸轮组1的受力最大，故以由推拉杆1、滚轮1、滚轮2、凸轮1以及杠杆1组合而成的凸轮组为研究对象。对凸轮组构件进行有限元网格划分，共计单元数258 603，节点数99161。

凸轮组的约束为:凸缘与左侧滚轮、凸缘与右侧滚轮设置面－面接触对;轮体内圈施加径向约束;杠杆支耳全约束;推拉杆两端铰链共12个自由度，分别约束除Y向以外的其他10个自由度;凸轮组的有限元计算模型如图6所示。

有限元静力接触分析时在推拉杆两端刚性区域处施加FY方向最大载荷。凸轮组中推拉杆两端的2个刚性区域存在2个自由度，对2个工况施加最大载荷进行静力计算，两个工况分别为:F，99158，FY，－3030.6146;F，99159，FY，－2990.5752。

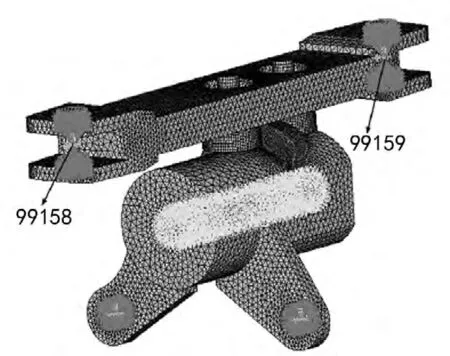
图6 凸轮组的有限元计算模型

图7 给出了刚性区域节点99 158施加力F1=－3 030.6146 N时凸轮组的等效应力云图。由图可知，等效应力较大部位在左侧滚轮阶梯轴处及凸缘与左侧滚轮接触区域的应力集中处，最大值分别为78.966 MPa和56.702 MPa。图8给出了刚性区域节点99 159施加力 F2=－2 990.5752 N时凸轮组的等效应力云图。由图可知，等效应力较大部位也在左侧滚轮阶梯轴处及凸缘与左侧滚轮接触区域的应力集中处，最大值分别为78.245 MPa和 55.918 MPa。

图7 节点99 158施加力F1时的等效应力

3.2 侧板的S－N曲线

凸轮组中滚轮、凸缘、推拉杆、杠杆等材料修正S－N曲线的相关参数如表2所列。

根据表2和修正S－N曲线的程序，计算得出:

滚轮材料三个转折点分别为(337.7，739)、(933776.6，189)、(109，98);凸缘材料三个转折点分别为(820.9，487)、(935531.8，146)、(109，76);推拉杆材料三个转折点分别为(14015.6，196)、(942056.2，96)、(109，50);杠杆材料三个转折点分别为(7918.9，239)、(940639.1，106)、(109，55)。

图8 节点99 159施加力F2时等效应力

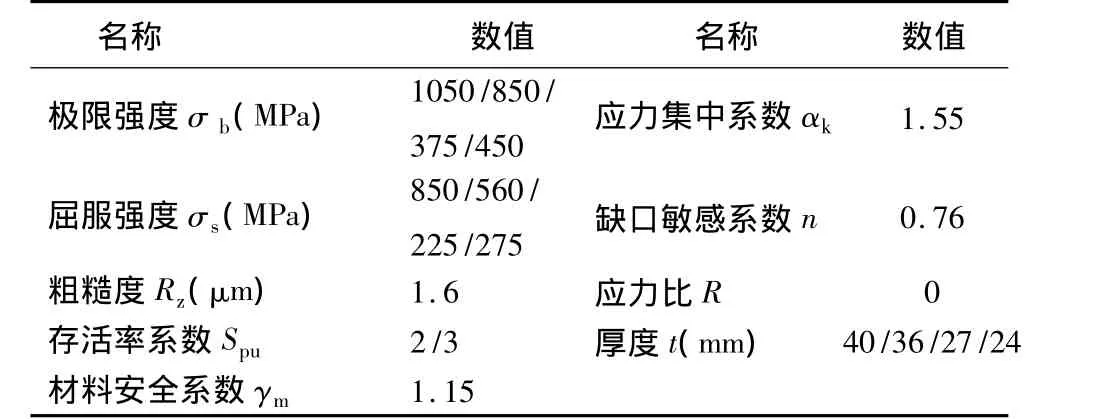
表2 凸轮组材料修正S－N曲线的相关参数

图9 凸轮组构件材料的修正S－N曲线

3.3 疲劳寿命计算

在疲劳分析软件FE－SAFE中，读入凸轮组接触模型的有限元分析结果，设置变量单位后生成一个应力集。因为在有限元接触分析时，在推拉杆两端施加的推力分别为 F1= －3 030.6146 N、F2= －2 990.5752 N，因此将凸轮组推拉杆两端的载荷历程文件分别对应地除以F1和F2，即可作为疲劳寿命分析时凸轮组的载荷谱。将单一工况的载荷历程分别与应力集相结合，定义如下以一年为单位的疲劳载荷文件。

# .ldf file created by fe－safe 5.4 －03［mswin］

INIT

transitions=Yes

END

#Block number 1

BLOCK n=67160，scale=1

lh=E:DaoChaTuLunZu xt54ct1 － ct13.txt，signum=2，ds=2，scale= －0.000334384

lh=E:DaoChaTuLunZu xt54ct1 － ct13.txt，signum=3，ds=1，scale= －0.000329966

END

凸轮组疲劳寿命分析时，设计寿命设置为50次循环，即为50年。采用Goodman平均应力准则修正后的最大主应力－疲劳寿命算法，对凸轮组进行疲劳寿命分析。图10和图11分别给出了凸轮组的对数疲劳寿命分布云图和安全系数分布云图。

图10 凸轮组的对数疲劳寿命

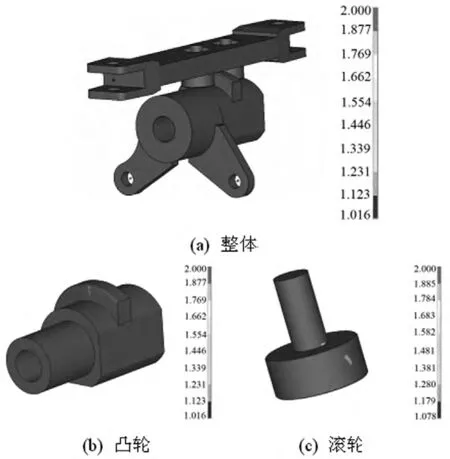
图11 凸轮组的疲劳安全系数

由图10可知，凸轮组的疲劳寿命对数值最小为1.754，出现在凸缘与左侧滚轮的接触面处，疲劳寿命以年表示为Nlife=101.754=56.75年。图11给出了凸轮组在50年设计寿命条件下的疲劳安全系数分布云图，其疲劳安全系数最小值为1.016，出现在凸缘与左侧滚轮的接触面。

4 结论

(1)介绍了以名义应力分析法及相应的材料疲劳特性曲线的疲劳寿命分析，并建立了侧板构件材料和凸轮组各构件材料相应的修正S－N曲线。

(2)在ANSYS中，建立了侧板及凸轮组的有限元分析模型，进行静力计算。通过FE－SAFE软件，结合静力计算结果及动力学仿真结果，对侧板和凸轮组进行了疲劳寿命计算。

(3)侧板的疲劳寿命为71.94年，最小疲劳安全系数为1.031，凸轮组的疲劳寿命为56.75年，最小疲劳安全系数为1.016，满足道岔侧板变形装置设计寿命50年的要求。

［1］ 靳晓波.重庆跨座式单轨车辆关节道岔通过性能研究［D］.北京:交通大学，2007.

［2］ 郭 凡，杨永清，刘国军，等.跨座式单轨交通关节可挠型道岔荷载试验研究［J］.铁道建筑，2010(10):8－10.

［3］ 陈传尧.疲劳与断裂［M］.武汉:华中科技大学出版社，2002.

［4］ 李舜酩.机械疲劳与可靠性设计［M］.北京:科学出版社，2006.

［5］ 姜年朝.ANSYS和ANSYS/FE－SAFE软件的工程应用及实例［M］.江苏:河海大学出版社，2006.

［6］ 风力发电机组规范［S］.中国船级社，2008.

［7］ Guideline for the certification of wind turbines［S］.Germanischer Lloyd，2010.