基于邓肯－张本构的后装压缩式垃圾车车厢有限元分析*

彭 旋，唐华平

(中南大学机电工程学院，湖南长沙 410083)

0 引言

后装压缩式垃圾车是城市中最常见的环卫车型，在垃圾车装卸载垃圾的过程中，垃圾及填料器产生的载荷会加载到车厢上，从而影响垃圾车车厢的使用寿命，但由于垃圾成分复杂使得垃圾车在进行加卸载时的受力也很复杂导致对垃圾车进行力学分析比较困难，笔者以建立压缩垃圾本构模型为基础，使用ANSYS软件对后装压缩式垃圾车满载挤入工况进行有限元仿真分析，得到相应工况下垃圾车车厢的应力分布情况并与现场试验结果相对比，验证了有限元模型的正确性，为以后进行压缩式垃圾车车厢的应力分析提出了一种新方法。

1 压缩垃圾模型的建立

后装压缩式式圾车主要运载对象为城市生活垃圾。城市生活压缩垃圾成分复杂力学特性难以确定，经研究表明［1］压缩垃圾的力学特性与土壤的力学特性非常的相似，垃圾在被压缩的过程中，其应力应变曲线表现为双曲线，且具有加工硬化特性，符合一般土壤的应力应变曲线，故可以使用土体力学中的邓肯－张本构模型模拟垃圾的应力应变关系。邓肯－张模型是国内外广泛采用的岩土模型，其应力应变曲线为双曲线，主要优点是可以利用常规三轴固结排水剪试验确定模型参数，参数测试简单，应用方便。

1.1 邓肯－张E－B本构模型

Duncan和Chang根据常规三轴试验的结果提出了在某一围压σ3下，在变形过程中t时刻土体体积模量和弹性模量可以表示为:

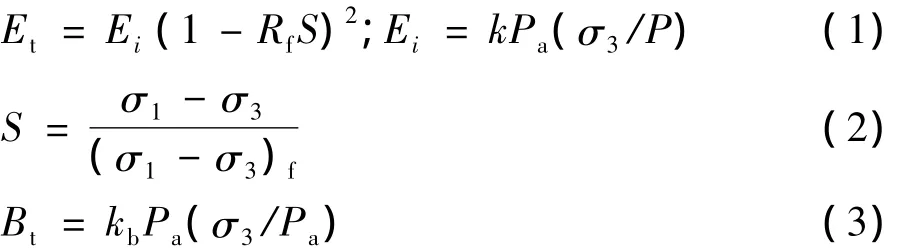
由摩尔库伦定律有:

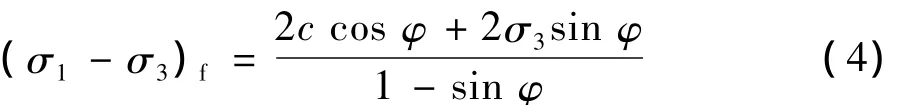
式中:Rf为材料破坏比;Ei为初始弹性模量;Pa为大气压;k为初始切线模量数;Kb为体积模量系数;S为当前材料的应力水平［2］。

对于三维情况［3］，在应力水平 S的计算中引入中间主应力，用广义剪应力q代替(σ1－σ3)，用平均主应力 p代替 σ3，用三维 Mohr－Coulomb准则 qf代替(σ1－σ3)f，则有:

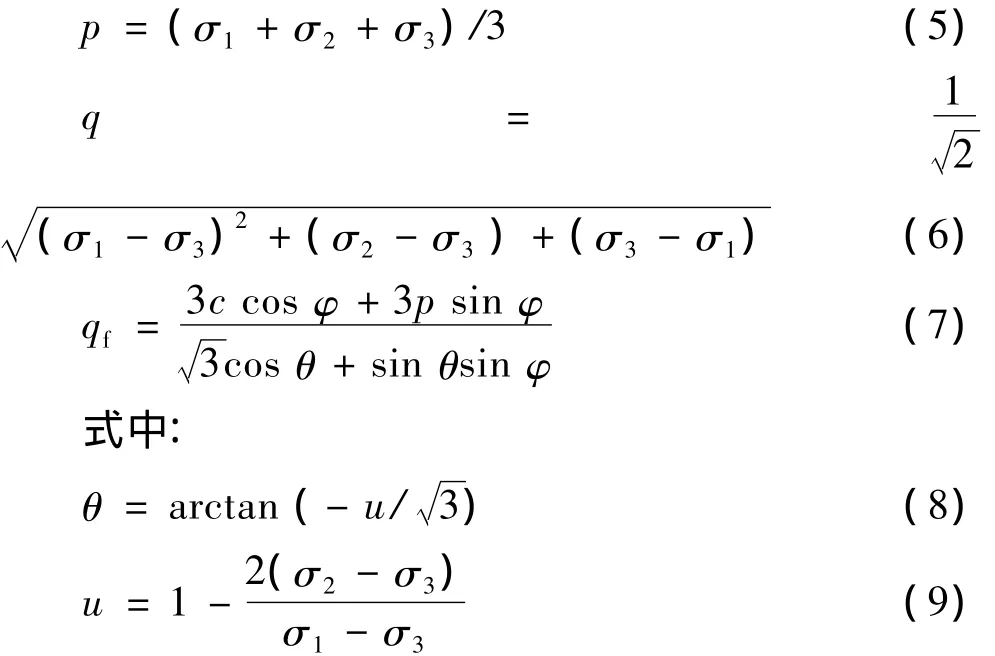
将式( 5) ～ ( 9) 代入原邓肯－ 张模型中，则土体的切线模量为:

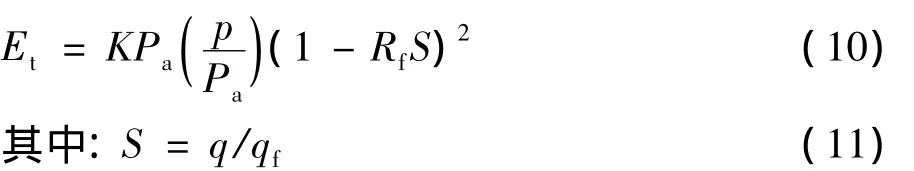
1.2 计算参数及有限元模型的建立

根据实验结果，垃圾车车厢装满垃圾时，车厢前后的上部区域都未填充垃圾，如图1所示，但由于后上部未充满垃圾区域很小可视为垃圾已充满该区域，ANSYS中建立垃圾有限元模型如图2所示。

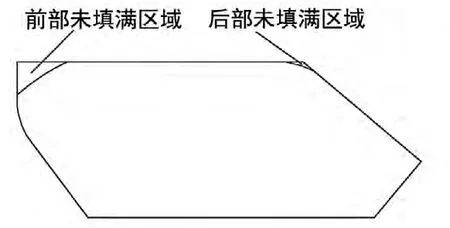
图1 垃圾未充满区域

图2 压缩垃圾模型

将式(5)～(9)代入原邓肯－张模型中，则土体的切线模量为:

垃圾在被压缩过程中，随着压缩次数的增加垃圾的密度也会随之增加当压缩次数达到一定数值时垃圾密度的变化很小［4］，如图3所示。

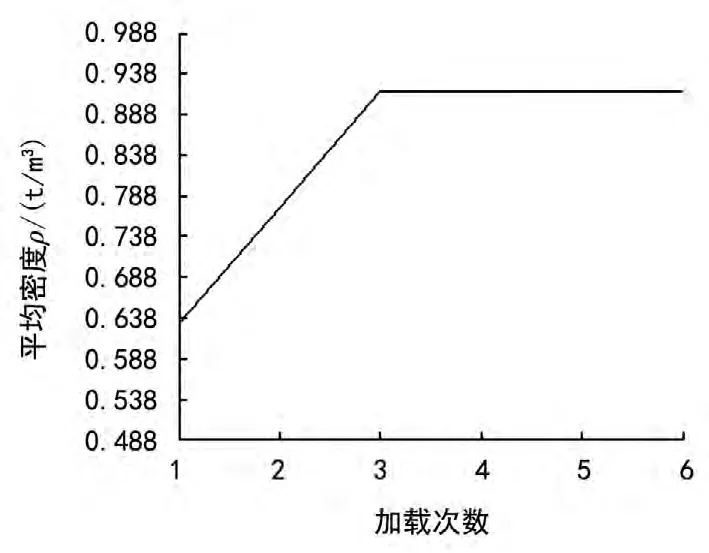
图3 垃圾压实密度与装载次数关系曲线

垃圾车在每次装载过程中推铲会往后移动一段固定距离，假设每一次装载压缩后的垃圾密度视为均匀分布，进行完第三次压缩后垃圾密度随装载次数变化很小可视为密度不发生变化，根据图3曲线，设斜线斜率为k。垃圾的总体积为11.5 m3，实验中垃圾总质量为9 t，第一次压缩的压缩垃圾位于车厢最前端，该区域上部未填满垃圾，测得体积v1=1.68 m3，第2～5次压缩的垃圾体积分别相等，可以测得体积分别为v2=1.74 m3，第六次压缩垃圾的体积v3=2.86 m3，根据体积与密度的计算有:

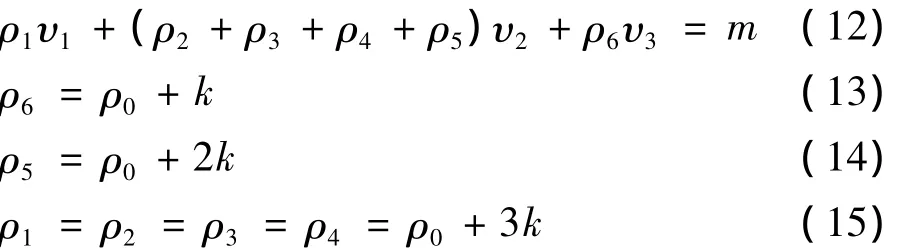
式中:ρ1、ρ2、ρ3、ρ4、ρ5、ρ6分别为第 1 次到第 6 次加载的垃圾密度，ρ0为垃圾的初始密度，v1为第一次加载的垃圾体积，v2为第2次到第5次分别加载的垃圾体积，v3为第六次加载的垃圾体积，k为图3曲线中的斜率，m为压缩垃圾的总质量。

计算得到垃圾根据压缩次数得到的垃圾密度分布图如图4所示。邓肯－张E－B本构模型在进行计算时需要用到八个参数，所有参数都可以通过对垃圾进行三轴试验获得。取垃圾初始孔隙比为2.0，压缩垃圾的邓肯－张E－B参数如表1［5］。

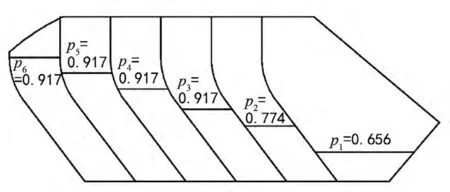
图4 垃圾密度分布图

表1 压缩垃圾邓肯－张E－B参数孔隙比e=2.0

2 ANSYS建模和分析

2.1 单元及参数定义

建立模型使用的单元及材料如表2，3所列。

表2 模型中使用的单元

表3 模型中定义的材料属性

垃圾车车厢厢壁以及加强筋为薄壁壳体类，加载后受平面法向压力，故使用壳体(Shell)单元，箱体的钢板和型钢使用相同的钢铁材料。垃圾与厢体的相互作用通过在垃圾与厢体之间施加接触单元来实现［6］。

2.2 边界条件条件

对于车厢模型根据模型的尺寸使用面单元自由网格划分，对于垃圾模型考虑到材料的特性以及接触的收敛，采用六面体网格进行SWEEP网格划分。

垃圾车车厢通过底架与主车体相连接，在车厢与汽车大梁接触处设置全约束，推铲与支撑架接触处设置全约束，约束如图5所示。

2.3 满载挤入工况载荷计算

在满载挤入工况下垃圾车车厢受到垃圾的挤入力F1、压缩力F2、重力G2以及填装器重力G1的作用力［7］，如图 6 所示。

图5 有限元分析模型及边界约束

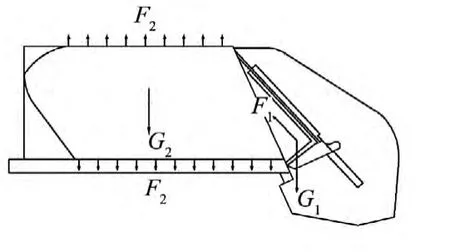
图6 车厢满载挤入工况受力情况

垃圾车在压缩的过程中通过刮板对垃圾产生挤入力，挤入力可分解为水平分量 Fb1和竖直分量，其中竖直分量Fa1克服区域C垃圾自重Gc后最终传递到顶板，如图7所示。假定挤入力均匀地施加到顶板区域A，则顶板垃圾挤入载荷计算如图7。

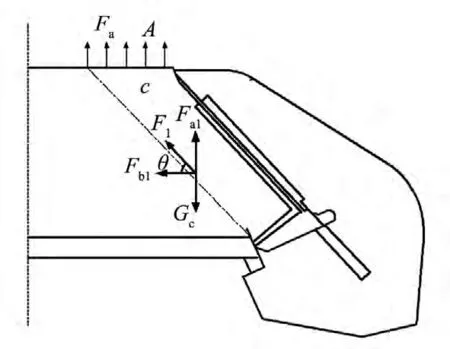
图7 顶板挤入载荷受力区域

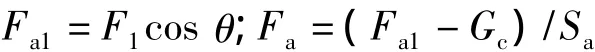
式中:F1为垃圾挤入载荷，Gc为C区域垃圾重量，Sa为A区域顶板面积。

邓肯－张模型是基于轴向加载的三轴实验提出来的［9］，需要对垃圾进行轴向加载，轴向载荷Fb1大小为挤入力F1的水平分量。同时填料器对车厢的载荷通过铰点、密封条和锁紧机构传递给车厢，将填料器对密封条的压力力视为均匀分布其大小为重力G1在垂直于密封条上的分量，满载挤入工况受力情况如表4所列。

表4 满载挤入工况车厢受力情况

2.4 计算结果与分析

根据表4中的工况对车厢加载计算，得出应力与位移云图，如图8所示，从计算结果可以看出来车厢所受最大应力在车厢尾部顶板处，车厢尾部受力比较大，前部受力较小，这与车厢最后一次加载尾部受力较大的实际情况是相符的。

图8 车厢应力云图

3 实验测试与计算结果对比

为了验证计算结果以及有限元模型的准确性，需要对垃圾车在满载挤入工况下的车厢进行应力测试，并将测试结果与计算结果进行对比验证有限元模型以及压缩垃圾本构模型的准确性。

试验测试时，在垃圾站垃圾车连续完成装载工况刮板装载垃圾至极限位置，在车厢顶板、侧板、一共选取15个主要点进行应力测试，测试三次取平均值。测试点位置如图9，各测点均布粘贴45°应变花。

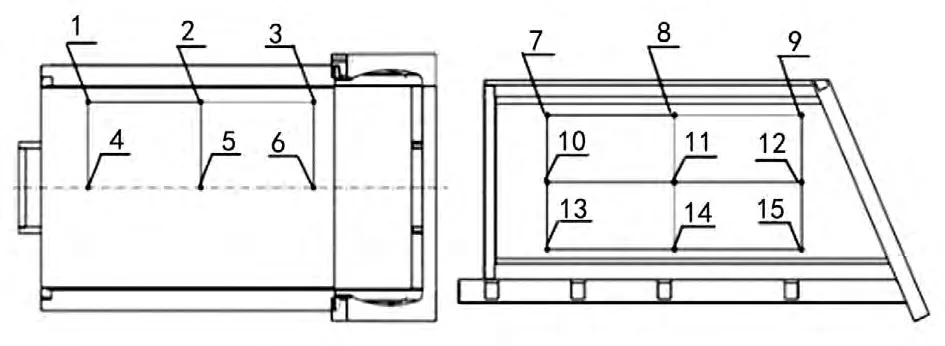
图9 车厢侧板与车厢顶板应力片位置

在满载挤入工况下车厢各点所测得的工作应力如表5、6所列，测点1和测点7处于垃圾未充满区域，未测到应力。

从表5与表6中可知，仿真与表对比可以看出误差基本控制在10%左右，证明有限元模型以及压缩垃圾本构模型是有效的。

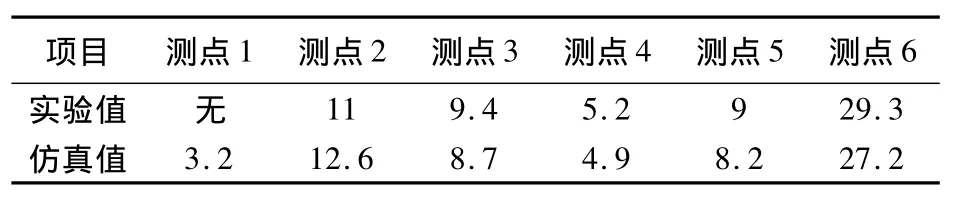
表5 车厢顶板实验与仿真应力比 /MPa

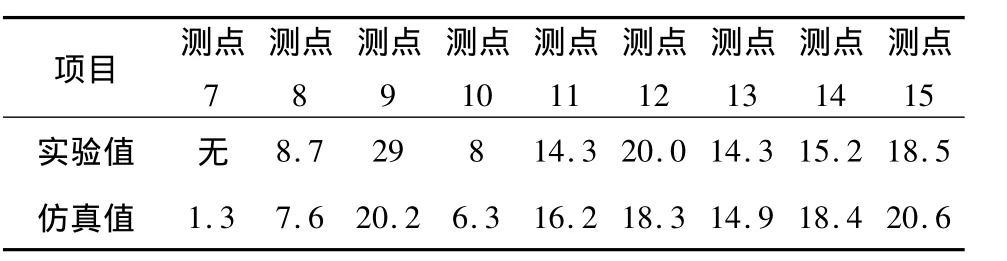
表6 车厢侧板试验与仿真应力比较 /MPa

4 结论

通过实验测试与计算仿真相互验证的结果表明:用基于邓肯－张模型建立的压缩垃圾本构模型对垃圾车车厢和压缩垃圾进行有限元分析是可行的。通过实验验证计算精度满足工程要求，可代替繁琐低效的试验工作。通过数值分析，可以对后装压缩式垃圾车车厢结构进行优化设计。

［1］ 张振营，杨云芳，陈云敏.城市生活垃圾的应力压缩曲线及压缩参数［J］.浙江理工大学学报，2008(1):119 －122.

［2］ 刘 招，苗隆德.基于APDL的混凝土面板堆石坝三维非线形有限元分析［J］.西北水力发电，2004:17 －20.

［3］ 卢廷浩，邵松桂.天生桥一级水电站面板堆石坝三维非线性有限元分析［J］.红水河，1996:20－23.

［4］ 黄仁华，赵由才.城市生活垃圾压实的工程试验研究［J］.同济大学学报(自然科学版)，2000(3):376－378.

［5］ 张振营，陈云敏.固体废弃物压缩特性及填埋场沉降研究［J］.岩土工程学报，2005(1):116－120.

［6］ 徐延海，贾丽萍.基于接触面几何的接触问题解法［J］.机械工程学报，2002，38(10):131 －134.

［7］ 丁继斌.后装压缩式垃圾车实验研究［J］.机械工程师，2005(10):65－67.

［8］ 陈树勋，王素暖，白 斌，等.压缩垃圾车结构的载荷描述与优化设计［J］.机械工程学报，2008(3):213－219.

［9］ 孔德志，朱俊高.邓肯－张模型几种改进方法的比较［J］.岩土力学，2004(6):971－974.