基于ESO的三相电压型逆变器终端滑模控制

郑恩让，赵兴旺

（陕西科技大学电气与信息工程学院，陕西 西安710021）

随着社会的发展，三相电压源型逆变器的应用范围越来越广泛，除了在传统的高压输电，不间断电源（UPS）等，也在医药，信息科技，各种专用电源，尤其是新能源如光伏与风力发电中发挥着越来越重要的角色。因此，逆变技术对于输出电能质量的保证至关重要。

逆变器为负载提供电源，其输出电压必须满足负载要求。所以其输出电压有效值与频率为逆变器首要控制目标。其次谐波含量（THD）必须满足国际要求（＜5%）。系统的动态性能与抗扰动与负载变化能力也是逆变器控制的重要衡量指标。传统的PI控制，虽然可以通过调节控制增益使得系统快速性，抗干扰等取得较好效果，但是控制增益往往要设置很大，可能导致系统的不稳定，稳态误差较大。

滑模控制是一种变结构控制，对干扰和参数摄动有自适应性，相比于其他非线性控制方法更容易实现［1］。其在电力电子变换器中得到了广泛的研究［2-3］。

为了加强三相电压型逆变器的控制效果，本文在三相逆变器d-q坐标模型基础上设计终端滑模控制方法，对d-q轴电压分别进行调节，再生成SPWM控制信号，实现对输出电压的控制。针对系统的不确定性及外部扰动设计ESO进行估计，ESO作为一种非线性状态观测器，适应性与鲁棒性比一般状态观测器强。对控制输出进行补偿，提高系统抗干扰与鲁棒性，同时滑模控制切换增益减小，减弱了抖振。针对所设计的控制系统，利用Matlab进行了仿真验证。

1 三相电压型逆变器的数学模型

图1 为带有输出LC 滤波器的三相电压型逆变器电路图。

图1 三相电压源型逆变电路Fig.1 Three-phase voltage source inverter circuit

假定图1 中的三相电路是完全对称的，且其开关元件为理想元件，由于电感的等效阻抗很小，在此忽略。根据输出电压电流关系可得三相三线制电压型逆变器交流侧电压电流方程：

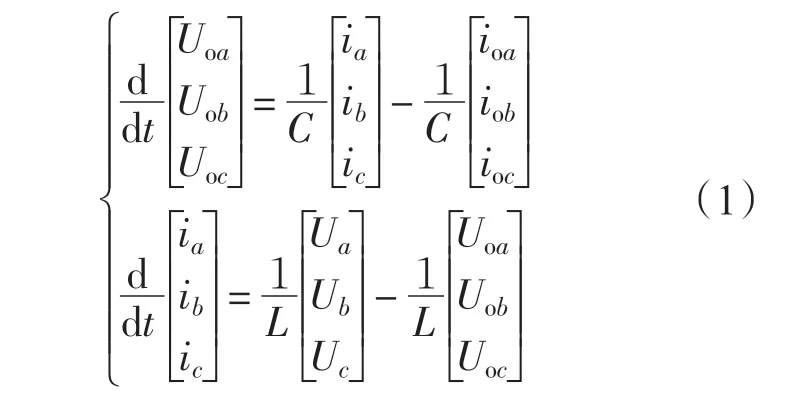
三相坐标系下的控制量多，控制方法较为复杂，控制效果普遍不理想。本文采取基于三相电压型逆变器d-q 坐标模型控制方法，由于d-q轴各分量为直流量，便于调节，简化了控制结构。三相逆变器输出侧在d-q 坐标系下的模型为［4］

式中：Ud,Uq为三相逆变电路输出侧d-q轴电压；Uod,Uoq为负载d-q轴电压；iLd,iLq为滤波电感上d-q轴电流；id,iq为负载d-q轴电流。

基于式（2），本文通过设计ESO 与Terminal滑模控制，实现对输出电压的有效控制。

2 ESO设计

2.1 ESO基本原理

ESO（扩张状态观测器）与传统状态观测器的最大不同就是对于同一个对象，它比传统的状态观测器多了1 维状态。对于n 阶对象，它的输出为n+1维。使用时第n+1维状态是对系统不确定量综合的估计，所以常常被反馈到系统控制器的输入端，对不确定量进行补偿［5］。

对于受未知外扰的不确定对象：

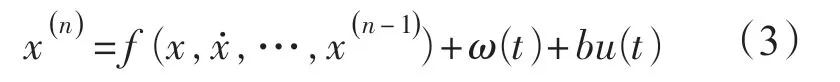
对此构造非线性系统

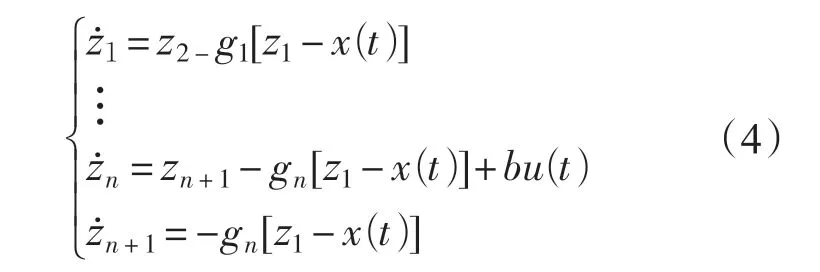
使这个以x（t）为输入的系统各状态z1(t),…,zn(t),zn+1(t )分别跟踪被扩张x(t),…,x(n-1)(t),x(n)(t )。其中g1(z),…,gn(z),gn+1(z)为待选取非线性函数，一般选择典型的fal 函数。这种观测器适应性与鲁棒性比一般状态观测器强。

2.2 三相电压型逆变器ESO设计

对于式（2）假设系统总干扰等效作用于输出Uod，Uoq上的扰动为dd,dq。则有：

基于式（5）设计ESO 对dd,dq进行观测，对系统控制输入进行补偿。

令

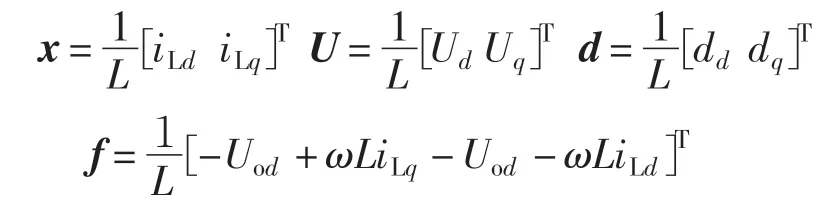
则式（5）可化为

根据文献［6-7］对d-q 轴分别设计二阶ESO如下：

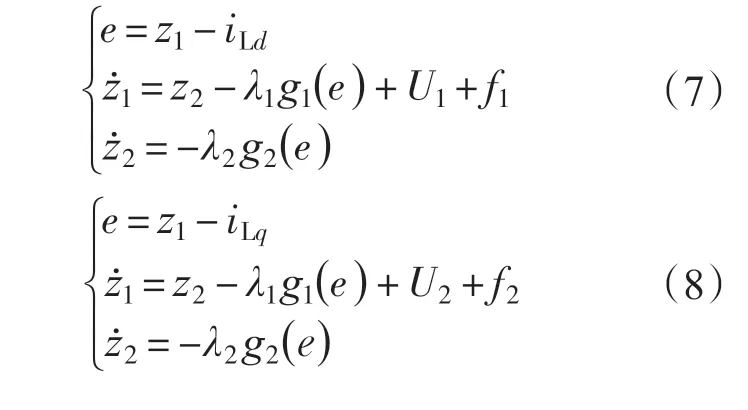
其中

i=1，2，ai为0～1 常数，越小跟踪越快；δ 越大，滤波效果越好，一般可取5～10倍的采样时间。

将观测出的扰动对跟踪误差进行补偿，利用修正后的误差设计滑模控制器，便可以达到对于系统扰动的补偿，增强系统的鲁棒性。

3 终端滑模控制器设计

Terminal 滑模控制，就是在滑动超平面的设计中引入了非线性函数，构造终端滑模面，使得滑模面上跟踪误差能够在有限时间内收敛到零［8］。

由式（2）可见，逆变器d-q 轴模型下耦合严重，是一个强耦合系统。对于滑模控制的设计来说增加了复杂性，因此首先对其耦合系统进行解耦，再进行滑模控制器设计将较为容易。

这里采用逆系统方法对其进行解耦，将原系统变为2 个无耦合的子系统，再分别进行滑模控制器设计［9］。逆系统方法以反馈线性化为基础［10］。

将积分逆系统和原系统相串联构成复合系统，称为伪线性系统。系统内部为非线性关系，但是输入输出却表现为线性关系，简化了控制器的设计。可设计出系统的逆系统方程。先求出伪线性系统输入：

由此可以求出逆系统方程为

原系统经过逆系统方法解耦变为2个线性子系统：

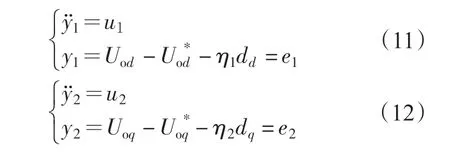
对解耦后的子系统设计非奇异终端滑模控制器。选取滑模面为［11］

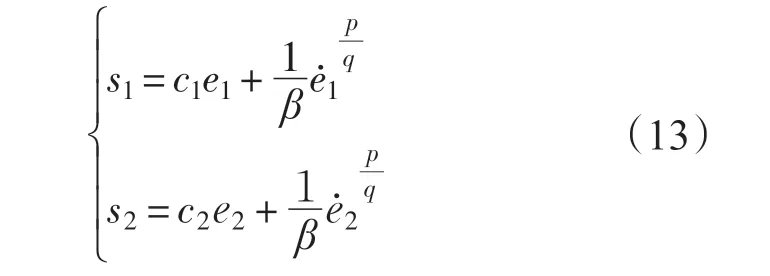
式中：c1,c2，β 为设计常数；p,q 为奇数且满足q ＜p ＜2q。

设计合适的变结构控制律，滑模面便可以在有限时间收敛至零［12］。

可以设计控制输入为

式中：k,k1为大于零设计参数。

通过设置合适的参数，调节控制输入，系统误差可在有限时间收敛至零。

4 仿真研究

为了验证所设计终端滑模控制器的有效性，对三相电压型逆变器进行Matlab 仿真。直流侧电压为600 V，输出滤波器电感L=1 mH，电容C=500 μF。控制器参数设定：p=11,q=7,β=0.1,k=8×106，c1=c2=8×106,k1=k2=500。输出参考相电压峰值为220 V，即

4.1 ESO扰动观测仿真

参 数 设 置 为：λ1=500,λ2=8×105,a1=0.5,a2=0.25,δ=2×10-5。

假设由于系统负载扰动及外扰等产生的未知扰动为

图2为ESO对d轴扰动（方波）的观测效果。

图2 ESO对d轴扰动观测波形Fig.2 Observed waveforms of ESO for the d-axis disturbance

图3 为q轴扰动（正弦波）观测效果。

图3 ESO对q轴扰动观测波形Fig.3 Observed waveforms of ESO for the q-axis disturbance

可以看出所设计的观测器除了在扰动跳变的时候有明显的误差。其他时刻几乎完全可以跟上。

4.2 逆变器滑模控制仿真

图4为逆变器空载时0.04 s突加5 kW纯阻性负载，而后0.07 s 又突然卸去负载时的A 相输出电压电流波形。可以看出波形在5 ms 左右迅速跟踪，效果良好。图5 为突加突减阻性负载A 相输出波形谐波分析，基波幅值为219.7 V，总谐波畸变率THD为0.03%。

图4 突加突减阻性负载时A相输出电压电流波形Fig.4 Output voltage and current waveforms of A-phase when resistive load changes abruptly

图5 突加突减阻性负载A相输出波形谐波分析Fig.5 Harmonic analysis for output waveforms of A-phase when resistive load changes abruptly

图6 为逆变器空载时0.04 s突加3 kW感性负载，而后0.07 s 又突然卸去负载时A 相的输出电压电流波形。可以看出波形在7 ms内迅速跟踪，效果良好。突加突减感性负载时A相输出波形谐波分析见图7，波形稳定时基波幅值为219.4 V，总谐波畸变率THD为0.08%。

图6 突加突减感性负载时A相输出电压电流波形Fig.6 Output voltage and current output waveforms of A-phase when inductive load changes abruptly

图7 突加突减感性负载时A相输出波形谐波分析Fig.7 Harmonic analysis for output waveforms of A-phase when inductive load changes abruptly

图8 为带25 kW负载输出电压参考值突变至260 V 时，波形响应曲线。可以看到本文方法输出电压在1/4 个周期内达到稳定正弦波，而PI 控制方法则大约需要半个多周期时间，说明本文方法优于PI控制。

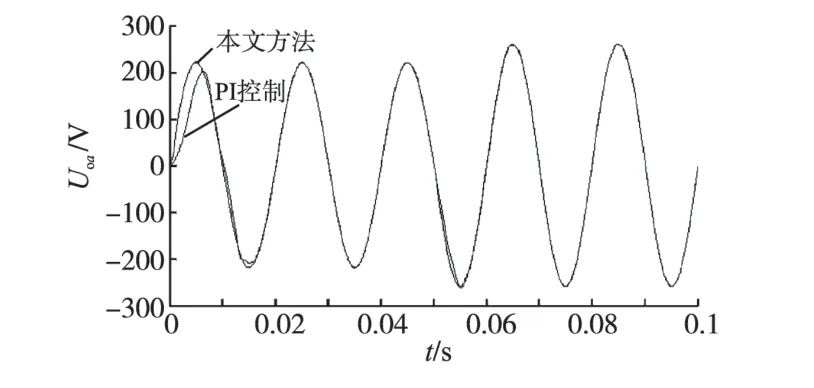
图8 电压指令突变时A相输出电压波形Fig.8 Output voltage waveform of A-phase when voltage command changes abruptly

图9 、图10为逆变器输出接三相整流器时，A相输出电压波形及电压指令突变时的响应曲线及THD 分析。0.04 s 电压指令由220 V 变为260 V，并在0.08 s撤去负载。

从图9、图10 可以看出，负载为整流器时输出电压接近标准正弦波，只在撤去负载时跳变一下，输出电压可以较快地跟踪电压指令，波形稳定时总谐波畸变率为0.15%，基波幅值为295.5 V，控制效果较为理想。

图9 电压指令突变时A相输出电压波形Fig.9 Voltage waveform of A-phase when voltage command changes abruptly

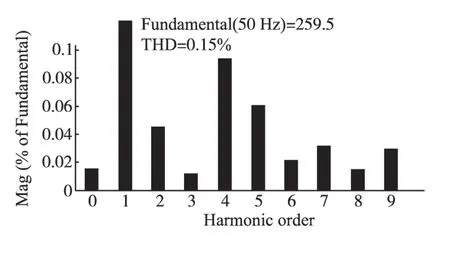
图10 指令突变时A相输出波形谐波分析Fig.10 Harmonic analysis for waveforms of A-phase when resistive load changes abruptly

图11 电压指令突变时d轴分量电压波形Fig.11 Voltage waveform of d-axis when voltage command changes abruptly

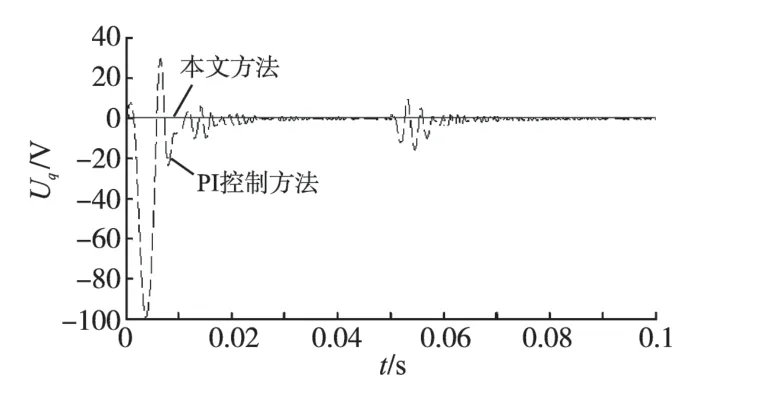
图12 电压指令突变时q轴分量电压波形Fig.12 Voltage waveform of q-axis when voltage command changes abruptly

图11 、图12为逆变器输出电压d-q轴电压响应波形，本文方法迅速跟踪d-q轴电压参考值，输出电压在较短时间达到稳态值，响应速度与稳态误差优于PI控制。

5 结论

本文基于三相电压型逆变器d-q 坐标系下的模型设计了基于ESO 的终端滑模控制器。对于系统总干扰设计ESO 进行了估计补偿，使得滑模控制中切换增益有效减小，达到减弱料振效果，增强系统鲁棒性；并对于解耦后的逆变器系统进行了终端滑模控制的设计，进一步简化设计。控制器对于系统外扰及负载等变化具有自适应性，能够快速跟踪给定，输出电压总谐波失真率较低。理论与仿真结果均表明此设计的有效性。

［1］ 刘金琨.滑模变结构控制MATLAB 仿真［M］.北京：清华大学出版社，2005.

［2］ 郑雪生，李春文.三相PWM电压型逆变器的积分滑模控制［J］.电工技术学报，2007，22（12）：105-109.

［3］ 张黎，丘水生.滑模控制逆变器的分析与实验研究［J］.中国电机工程学报，2006，26（3）：59-63.

［4］ 马皓，张涛，韩思亮.新型逆变器滑模控制方案研究［J］.电工技术学报，2005，20（7）：51-57.

［5］ 李勋，朱鹏程，杨荫福，等.基于双环控制的三相SVPWM逆变器研究［J］.电力电子技术，2003，37（5）：30-33.

［6］ 韩京清.一类不确定对象的扩张状态观测器［J］.控制与决策，1995，10（1）：84-87.

［7］ 王海强，黄海.扩张状态观测器的性能与应用［J］.控制与决策，2013，28（7）：1078-1081.

［8］ 袁雷，肖飞，沈建清，等.基于扰动观测器的不确定非线性系统非奇异终端滑模控制［J］.控制与决策，2014，29（2）：353-357.

［9］ 康忠健，孟繁玉，魏志远，等.基于扩张状态观测器的非线性变结构控制器研究［J］.电子电气教学学报，2007，29（5）：56-59.

［10］吴忠强，庄述燕，马宝明，等.基于逆系统方法的并网逆变器自适应模糊滑模控制研究［J］.电力系统保护与控制，2011，39（24）：1-7.

［11］吴热冰，李春文.一般非线性系统的构造性逆系统方法［J］.控制理论与应用，2003，20（3）：345-350.

［12］吴忠强，谢建平.带扰动观测器的网侧逆变器高阶终端滑模控制［J］.电机与控制学报，2014，18（2）：96-101.