变论域模糊PI在全范围调速系统中的应用设计
刘胜,刘江华
(哈尔滨工程大学自动化学院,黑龙江 哈尔滨150001)
异步电动机作为一个高阶、非线性、多变量、强耦合的被控对象,借助于矢量控制(vector control),通过坐标变换,以磁场定向,可以将其等效成一个直流电机模型,然后就可以按照对直流电机的控制方法对异步电动机进行控制[1]。PI控制由于算法简单、鲁棒性好、可靠性高,在异步电动机调速系统中使用比较普遍。但由于异步电动机的数学模型是非线性、时变的,在电机运行过程中,电机参数会发生变化,传统PI 控制很难得到比较好的动态和稳态性能。模糊控制(fuzzy control)作为一种智能控制方法,由于结构简单,设计方便,不需要被控对象精确的数学模型,而按照人类的知识、经验去构造控制规则、设计控制器,能够取得比较好的控制效果,近年来研究成果比较多。但其控制性能依赖于控制规则库的完备性与准确性,对于复杂非线性系统,获取完整的控制规则库比较困难,致使模糊控制器难以满足高精度控制要求。针对模糊控制的不足,文献[2]提出了变论域思想,在规则形式不变的前提下,变量的模糊论域在初始范围的基础上进行相应的伸缩变化,进而间接地增加误差较小区间的控制规则分辨率,提高控制器精度。但到目前为止,还没有一套公认的、简单有效的选择伸缩因子的方法。文献[3]针对几种变论域伸缩因子的选择方法,通过直流调速系统仿真对它们的性能进行了比较分析,证明基于误差分级选择伸缩因子的方法相对更好。
本文在基于误差分级选择伸缩因子方法的基础上,利用误差和误差变化率分区方法选择伸缩因子对变论域模糊PI控制器在三相异步电机矢量控制调速系统中的应用进行设计;另外为了改善变论域模糊PI控制器在临近稳态阶段由于控制规则切换造成的转速响应不平滑,在变论域模糊PI控制器中增加了一个信号调理环节。通过与传统PI、模糊PI 的控制效果比较,表明所设计的变论域模糊PI 控制器在异步电机全范围调速应用中抗干扰能力更强,动态品质和稳态精度更高。
1 三相异步电动机矢量控制系统
图1为三相异步电动机矢量控制系统的结构框图,控制过程包含4个环:速度环、转矩环、磁链环和电流环。给定转速ω*与反馈转速ω 的偏差经ASR(速度调节器),输出为期望的转矩;期望的转矩与电机的转矩估计量Te的偏差经ATR(转矩调节器)后,输出为定子电流的T 轴分量;给定的转子磁链与电机转子磁链的估计值Ψ 的偏差经AΨR(磁链调节器)后,输出为定子电流的M 轴分量经2R/3S 坐标变换(Park 逆变环、Clark 逆变换)后,最后转换为三相静止轴系下的定子电流分量在电流环滞环控制的作用下,产生PWM逆变器触发信号,进而控制三相异步电机的运行。另外,为避免换流时的直通现象,滞环宽度取左右不等[4]。

图1 三相异步电动机矢量控制系统结构框图Fig.1 Block diagram of vector control system for three phase asynchronous motor
2 变论域模糊PI控制器设计
2.1 模糊PI控制器设计
模糊PI 控制器是将模糊控制与PI 控制相结合的控制方法,控制器以误差e 和误差变化率ec作为输入,利用模糊控制规则在线对PI参数进行修改[5-7],图2为模糊PI控制器结构框图。

图2 模糊PI控制器结构框图Fig.2 Block diagram of fuzzy PI controller
修正后的PI参数如下式所示:

式中:kp0,ki0为初始PI 参数;Δkp,Δki为模糊控制器输出的修正值;kp,ki为修正后的PI参数。
对模糊控制器的输入e,ec,输出Δkp,Δki,进行模糊化处理,模糊分割数均取7,语言变量为NB,NM,NS,ZE,PS,PM,PB;e,ec 的论域取[-3,3],Δkp,Δki的论域取[-0.3,0.3],则量化因子和比例因子分别如下式所示:

式中:ke,kec分别为误差e 和误差变化率ec 的量化因子;λp,λi分别为模糊控制器输出修正值Δkp,Δki的比例因子;[emax,emin],[ecmax,ecmin],[Δkpmax,Δkpmin],[Δkimax,Δkimin]分别表示e,ec,Δkp,Δki的基本论域。
为方便设计,输入输出变量的基本论据都取对称的取值范围,其中emax=-emin=nN;而ec 的取值与电机转子的机械角加速度相同,所以取

输入输出变量的隶属度函数均采用交叠对称分布的三角形,在误差较小的论域选择底角大的三角形;在误差较大的论域,采用底角小的三角形。模糊控制规则表作为模糊控制的核心内容,其完备性和准确性直接影响模糊控制的效果,见文献[7]。
2.2 变论域伸缩因子选择
将变论域思想运用于模糊PI控制,利用误差及其变化率的大小选择各变量论域的伸缩因子,变论域模糊PI控制器结构框图如图3所示。

图3 变论域模糊PI控制器结构框图Fig.3 Block diagram of variable universe Fuzzy PI controller
图3 中αe,αec分别为模糊控制器输入变量e,ec 的论域伸缩因子;βp,βi分别为模糊控制器输出变量Δkp,Δki的论域伸缩因子。此时,变论域模糊控制器的量化因子和比例因子可以表示为
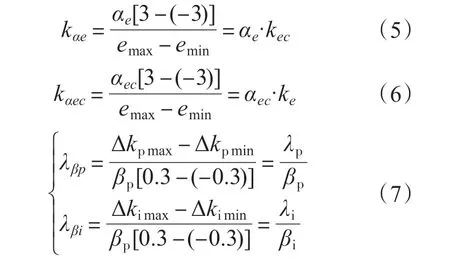
式中:kαe,kαec分别为论域伸缩后误差e 和误差变化率ec 的量化因子;λβp,λβi分别为论域变换后模糊控制器输出修正值Δkp,Δki的比例因子。
伸缩因子的选择作为变论域模糊PI 控制器的核心内容,目前相关文献中常用的方法有:基于函数形式选择伸缩因子、基于模糊推理方式选择伸缩因子、基于误差分级方法选择伸缩因子[3]。文献[3]通过直流调速系统仿真对它们的性能进行了比较分析,证明基于误差分级选择伸缩因子的方法相对更好,但没有考虑误差变换率的影响。因此,本系统在文献[3]基于误差分级方法的基础上,尝试通过基于误差及其变化率分区的方式选择伸缩因子,将输入变量e 的基本论域分为3个区间,并编号Ⅰ,Ⅱ,Ⅲ,即Ⅰ:[0,0.2emax]U[-0.2emax,0),Ⅱ:(0.2emax,0.6emax]U[-0.6emax,-0.2 emax),Ⅲ:(0.6emax,emax]U[-emax,-0.6emax);同时把ec的基本论域也分为3个基本区间,并编号A,B,C,即A:[0,0.4ecmax]U[-0.4ecmax,0),B:(0.4ecmax,0.8ecmax]U[-0.8ecmax,-0.4ecmax),C:(0.8ecmax,ecmax]U[-ecmax,-0.8ecmax)。通过仿真调试,伸缩因子选择值如表1 所示。变论域模糊PI 控制器仿真模型如图4所示。

表1 伸缩因子αe,αec,βp,βi 选择值Tab.1 The choice values of extension factor αe,αec,βp,βi

图4 变论域模糊PI控制器仿真模型Fig.4 Simulation model of variable universe fuzzy PI controller
2.3 “模糊控制规则”不平滑切换改善方法
变论域模糊PI控制由于模糊规则、隶属度函数、量化因子、比例因子的选择以及论域的划分都是根据操作人员的经验,往往导致实际应用过程中出现系统响应不平滑,局部波动现象。
为了改善变论域模糊PI 控制器在临近稳态阶段由于“模糊控制规则”切换造成的转矩响应有毛刺,致使转速响应不平滑(本系统变论域模糊PI 控制用在速度环),在变论域模糊PI 控制器中增加了一个信号调理环节。对控制系统进行离散化处理,则可得离散变论域模糊PI控制器的输出表达式如下:
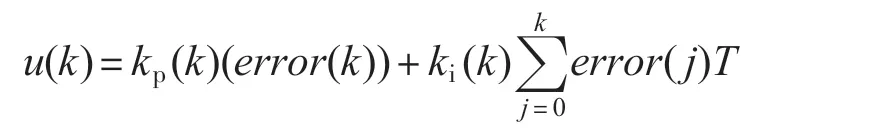
式中:T 为采样周期;k 为采样序号,k=1,2,…,error(k-1)和error(k)分别为第(k-1)和第k 时刻所得的偏差信号;kp(k),ki(k)分别为第k 时刻的比例系数和积分系数。
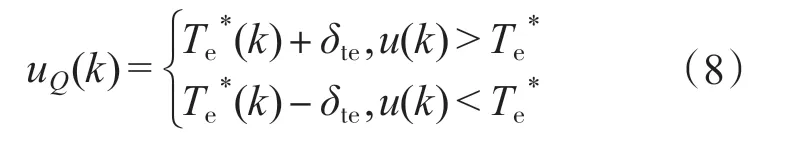
式中:EFZ,ECFZ分别为e,ec 的阀值,Te*(k)为第k 时刻的给定负载值;δte为临近稳态阶段u(k)围绕Te*(k)上下波动限宽。
3 系统仿真及结果分析
3.1 系统仿真参数
对异步电动机矢量控制系统进行仿真实验,采用的鼠笼式三相异步电机参数[3]为:额定功率2.24 kW,额定电压220 V,额定频率50 Hz,额定转速1 440 r/min,电机极对数pn=2,Rs=0.435 Ω,Rr=0.816 Ω,L1s=4.000 mH,L1r=4.000 mH,Lm=69.00 mH。
为了测试系统的动、静态性能和抗扰动能力,转子给定磁通为9.6 Wb,负载转矩给定初始值为0 N·m,1 s后负载转矩变为15 N·m,对给定转速分别为80 r/min,700 r/min,1 400 r/min 时进行仿真,仿真过程中ATR,AΨR 均采用传统PI控制器,ASR 先后采用传统PI 控制、模糊PI 控制、变论域模糊PI 控制。通过反复调试,最后得到的各控制器仿真实验参数如下:转矩调节器,kp=4.5,ki=30;磁链调节器,kp=4.8,ki=100;速度调节器为传统PI 控制器(给定转速为1 200 r/min 时),kp=3,ki=10;模糊PI 控制器,kp=4,ki=10,kp的基本论域为[-2,2],ki的基本论域为[-3,3];变论域模糊PI控制器,kp=4,ki=10,kp的基本论域为[-2,2],ki的基本论域为[-3,3]。
3.2 仿真结果及分析
根据以上给定仿真参数,可得仿真结果如图5~图8所示。
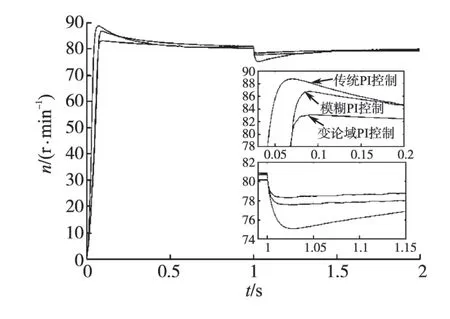
图5 给定转速n*=80 r/min时的转速响应Fig.5 Speed response when given speed n*=80 r/min

图6 给定转速n*=700 r/min时的转速响应Fig.6 Speed response when given speed n*=700 r/min

图7 给定转速n*=1 400 r/min时的转速响应Fig.7 Speed response when given speed n*=1 400 r/min

图8 给定转速n*=80 r/min时的转矩响应Fig.8 Torque response when given speed n*=80 r/min
对仿真结果(图5~图7)进行比较,比较结果如表2所示。
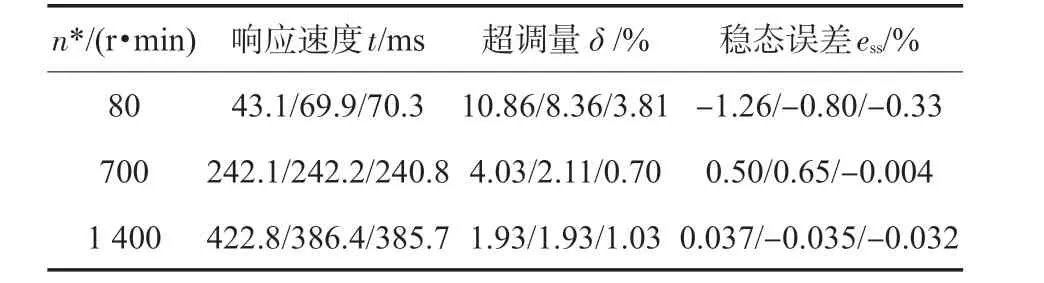
表2 仿真结果比较Tab.2 Comparison of simulation results
结合图5~图7和表2可以看出,当速度环采用传统PI 控制时,系统在高、中档段有比较好的调速性能,但在低档段有较大的超调(给定转速为80 r/min 时,超调达到了10.8%);当采用模糊PI 控制时,系统整体调速性能有所改善,但低档段仍有较大的超调,中档段稳态误差较传统PI控制还有所增加(给定转速为700 r/min 时,稳态误差增加了0.15%);当采用变论域模糊PI 控制时,系统调速性能有明显的改善,超调量和稳态误差都有明显的下降(给定转速为80 r/min时,超调量降到了3.81%;给定转速为700 r/min 时,稳态误差降到了-0.004%),高、中档响应速度也有所提高。另外,由图8 可以看出,变论域模糊PI 控制加入信号调理环节后,转矩毛刺得到了一定的抑制,在临近稳定阶段,转速响应也较平滑(见图5),但在其它阶段不平滑现象仍然存在,这需要从模糊控制规则本身进行研究。综合以上对仿真结果的分析,表明所设计的变论域模糊PI控制器是可行的,且在三相异步电动机全范围调速中超调小、响应快、稳态精度高,具有更强的适应性。
4 结论
在传统PI控制的基础上,利用误差和误差变化率分区方法选择伸缩因子,对三相异步电动机矢量控制系统的速度环进行了变论域模糊PI 控制器设计;另外,为了改善变论域模糊PI 控制在临近稳态阶段由于控制规则切换造成的转矩响应毛刺较多,致使转速响应不平滑现象,在变论域模糊PI 控制器中增加了一个信号调理环节。通过与传统PI、模糊PI的仿真比较,结果表明:所设计的变论域模糊PI 控制器在三相异步电动机矢量控制全范围调速系统中具有更好的适应性,不仅能提高转速响应的响应速度、降低超调量,且能明显地改善稳态误差,对工程中调速范围比较宽的调速系统设计具有一定的参考价值。
[1] 李华德.交流调速控制系统[M].北京:电子工业出版社,2004.
[2] 李洪兴.变论域自适应模糊控制器[J].中国科学,1999,29(l):32-42.
[3] 谭兵文,李春文.几种变论域伸缩因子选择方法的比较[J].科学技术与工程,2013,13(4):908-911.
[4] 洪乃刚.电力电子、电机控制系统的建模和仿真[M].北京:机械工业出版社,2010.
[5] Amrane,Louri M,Larabi A,et al.A Fuzzy Model Reference Adaptive System Control for Induction Motor Drives[C]//Proceedings of the 3rd International Conference on Systems and Control,Algiers,Algeria,2013:29-31.
[6] Hassan Farhan Rashag,Koh S P,Ahmed N Abdalla,et al.Modified Direct Torque Control Using Algorithm Control of Stator Flux Estimation and Space Vector Modulation Based on Fuzzy Logic Control for Achieving High Performance from Induction Motors[J].Journal of Power Electronics,2013,13(3):369-378.
[7] 杨瑜,庄圣贤.基于DSP 的模糊PID 矢量控制变频器的研究[J].设计参考,2010,12(10):45-47.

