基于最小二乘法的电机转速测量
华强,颜钢锋
(浙江大学电气工程学院,浙江 杭州310027)
现代伺服控制系统中主要采用永磁同步电机作为执行机构,并普遍采用基于矢量控制的电流、速度和位置三闭环控制[1]。为实现高性能伺服系统,转速检测的精确性和快速性非常关键。
光电编码器是一种常用的转速传感器,测速方法主要有:1)M 法:通过测量一段时间内的脉冲个数来计算转速,适用于高速场合;2)T 法:通过测量编码器相邻两个脉冲的时间间隔来计算转速,适用于低速场合;3)M/T法:是上述两种方法的综合,在各个速度段都有不错的精度,但实现起来需要硬件资源多,软件也复杂[2]。
在伺服控制系统中,主要采用的是M 法测速,这是因为:1)永磁同步电机需要获取准确的转子位置信号来进行运算,因此编码器分辨率一般较高;而且系统本来就实时测量编码器脉冲数,因此适合采用M 法;2)控制系统中往往希望控制时间固定[3]。M 法测速时间是一定的,故控制时间可保证固定;而T 法测速时间跟电机转速有关。
由于编码器脉冲计数存在量化误差,在低速场所下M法得到的脉冲数将很小,从而导致测量精度低。编码器精度一定时,为提高测量精度,需要增长测量窗口时间,这又会导致测量延迟,影响系统动态性能。为提高编码器的测速性能,很多方法被相继提出[4-7]。文献[4-5]讲述了变M法测速方法,但该方法低速测量延迟长,影响低速测量的实时性。文献[6]将观测器理论应用于转速估计,测量精度高且补偿了测量的延迟。但该法测量精度受系统转动惯量影响很大,实用性较差。文献[7]提出了多种根据离散数据估计瞬时速度的方法,有利用泰勒展开式、后向差分推导以及拟合法,一定程度可提高测量精度。
本文在文献[7]数学理论基础上,将最小二乘法曲线拟合应用于电机转速测量,推导了最小二乘法测速原理。之后比较了两种不同阶次最小二乘法的测速特性,得出不同阶次最小二乘法适用于不同电机运行状态,最终提出了一种综合最小二乘法来提高测速性能。通过Simulink 仿真和在永磁同步电机控制平台上实验,结果证明了该综合最小二乘法测速精度高,动态延迟小。
1 最小二乘法测速原理
1.1 最小二乘法测速理论
在永磁同步电机矢量控制系统中,通过处理器的定时器的编码器计数功能实时获取编码器脉冲计数,可作为电机的转子位置信号。若每隔一定间隔时间T 读取位置信号,则可以得到最近的m组转子位置反馈数据(ti,yi),其中i=1,2,…,m,ti表示时间,且ti=T· i,yi表示ti时刻位置。这些位置反馈数据一般都带有误差,将这些数据通过曲线拟合法得到位置函数,一定程度上减小误差的影响,对位置函数进行求导等运算便可得转速。
最小二乘法是根据拟合曲线和数据的偏差平方和最小原则来求拟合曲线,是一种常用的曲线拟合方法。转子位置信号可采用代数多项式拟合,拟合表达式为
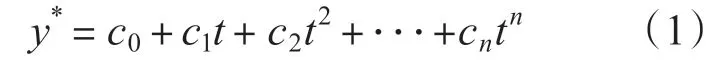
式中:t 为时间;ci为系数,i= 1,2,…,n;n 为拟合多项式阶次,n=1,2,3,…,且满足n+1<m。将ti=T· i 代入式(1)得ti时刻拟合位置值:



式中:A为m·(n+1)矩阵;M为n+1方阵。利用最小二乘法原理,待测系数C计算公式为[7]
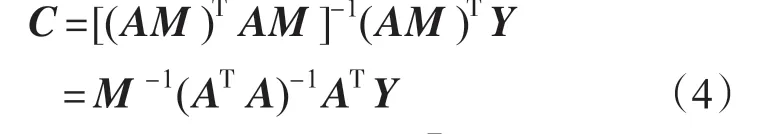
其中 Y=[y1,y2⋅⋅⋅,ym]T
式中:Y为各时刻实际测得位置数据。假设伺服控制系统中每转编码器脉冲数为P,由式(1)~式(4)求得电机当前时刻tm转速ωm为

其中转速单位为r/min,B 计算公式为

只要确定数据个数m 和最小二乘法阶次n,则矩阵A 便确定了,利用式(5)、式(6)便可以求出电机当前时刻的电机转速。该方法计算量主要体现在B 的求取,B 可通过Matlab 等工具计算得出。算法实现时,只需编写简单的代数浮点数运算,因此最小二乘法测量转速容易数字化实现。
1.2 最小二乘法测速比较
最小二乘法测速的准确性取决于拟合的转子位置信号曲线是否与实际接近,这就依赖于最小二乘法中阶次n 和数据个数m 的选取。最小二乘法中的阶次n 决定了拟合曲线的特性,需要根据实际应用情况选取,例如当拟合的位置信号成一条直线时,n 适合取1。最小二乘法中的数据个数m 也需要折中选取,m 过小会使曲线拟合效果变差;而m 越大,一定程度上可减小量化误差的影响,但也会影响测量实时性以及算法的计算量。
下面采用6个数据分别拟合1阶最小二乘法(LSF1/6法)、2阶最小二乘法(LSF 2/6法),即m=6,n=1,2。根据式(5)得测速公式如下。
LSF1/6法:

式中:y6为当前位置信号;y5,y4,y3,y2,y1分别为前T,2T,…时位置;P为电机1圈编码器脉冲数;T为测量周期。
为对比LSF1/6 和LSF2/6 法的测速性能,进行仿真实验。仿真基于永磁同步电机控制系统,给定速度为200 r/min,采样周期为1 ms。仿真结果如图1所示,可知LSF1/6法在转速稳定后具有很高的测量精度,但转速动态变化时滞后于实际转速,实时性较差;LSF2/6 法在转速动态变化时延迟小,但在转速稳定后测量精度不如LSF1/6法。

图1 LSF1/6和LSF2/6法测速仿真结果Fig.1 Simulation results of LSF1/6 and LSF2/6
1.3 综合最小二乘法
从前面的分析可知,当电机转速快速变化时,选取LSF2/6 法测速可减小测速延迟,提高动态测量精度;而当转速稳定后,选取LSF1/6 法测速可获得更高测量精度。伺服系统运行过程中,电机将频繁处于启动、稳定转速、制动的交替运行状态[10],为提高测速精度和实时性,需综合使用LSF1/6和LSF2/6法来测速。
分析电机的启动和制动过程[10],电机启动、稳定、制动和停止状态下的转速和转速误差曲线如图2 所示,图2 中0—t2时间段,给定转速为n*,t2—t4时间段,给定转速为0。可知,电机运行稳定和停止状态时,转速误差e 和转速误差的变化率˙接近为0,而电机运行启动和制动状态下时,e 和不同时接近0。因此可将e 和˙大小作为转速是否稳定的判断依据,即可作为测速方法选取依据。
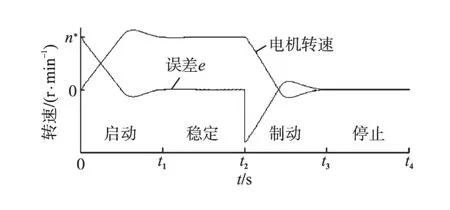
图2 不同电机状态下转速和转速误差曲线图Fig.2 Speeds and speed errors of different motor running state
2 仿真和实验
2.1 仿真
为验证综合最小二乘法的测速性能,采用Simulink 对M 法和综合最小二乘法进行仿真对比。永磁同步电机控制系统仿真模型见图3,给定转速为200 r/min。编码器500 线,采用4 倍 频技术。M 法采用1 ms 和6 ms 的间隔时间(简称M1法和M6法),综合最小二乘法(简称综合LSF 法)综合了LSF1/6 和LSF2/6 法,采样周期取为1 ms,e 阈值设为5 r/min,˙的阈值设为2 r/min。
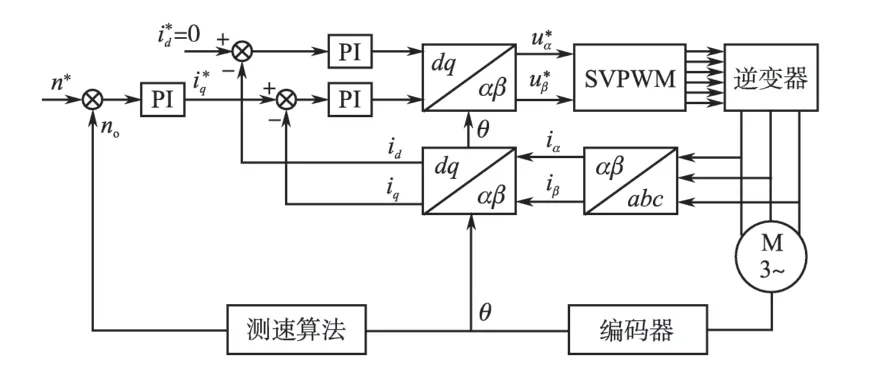
图3 永磁同步电机控制系统仿真模型Fig.3 Simulation model of permanent magnet synchronous motor control system
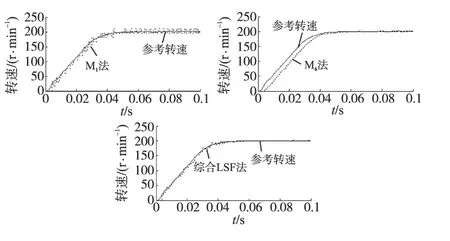
图4 各测速方法的仿真结果Fig.4 Simulation results of different speed measurement methods
1)测速精度对比。测速结果如图4所示,可知M1法测速误差较大;M6法由于增大了间隔时间,虽然在转速稳定时误差小,但是在转速变化过程中误差大,且一直滞后于参考转速;而综合LSF法在全过程的误差都较小。
2)测速动态性能对比。图5为转速快速变化时间段各测速方法仿真结果,由图5可得:综合最小二乘法测速动态响应最快,而M6法滞后最大。
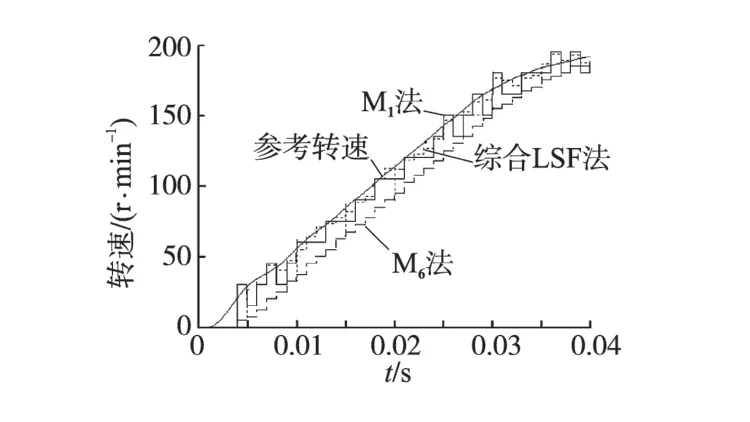
图5 转速动态变化时各测速方法的仿真结果Fig.5 Simulation results of different methods at speed changing
为定量分析测量方法的动态测量性能,定义测量延迟为测速方法测的转速与参考转速相同时的时间差。三者的测量延迟如表1 所示,对比M1法和M6法,可知M 法测速随着间隔时间的增大,动态延迟变大;而综合最小二乘法动态延迟最小,动态性能最好。

表1 各测速方法的测量延迟Tab.1 Measurement delay of different methods
2.2 实验
为进一步验证综合最小二乘法测速性能,在永磁同步电机控制平台上实验。电机接有500线和2 500 线的增量式编码器,其中500 线编码器用于测速方法对比,2 500 线的编码器测得转速用于参考;控制器处理芯片采用带有浮点数运算能力的STM32F407VGT6,它带有编码器接口,并对编码器信号进行4 倍频。两种方法采样周期都为1 ms,综合LSF 法e 阈值设为10 r/min,e˙通过最近2 次的转速误差e 之差得到,阈值设为5 r/min。
电机给定转速400 r/min,从静止启动电机。两种方法测速结果如图6 所示,由图6 可知不论是在电机转速动态变化时还是在转速稳定时,综合LSF 法测速误差都比M1法小。实验表明了综合最小二乘法在提高稳态测速精度的同时,也保证了测速的动态性能。
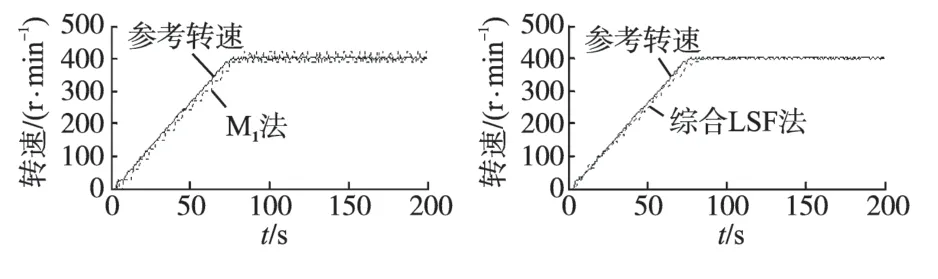
图6 M1法和综合LSF法的实验结果Fig.6 Experiment results of M1 method and multiple least square method
3 结论
本文应用了一种基于最小二乘法曲线拟合的测速方法,对比到不同阶次最小二乘法的测速性能,得出不同阶次最小二乘法适用于电机不同运行状态,故最终提出了一种方便可行的综合最小二乘法来提高测速性能。将此综合法应用于永磁同步电机控制系统中,仿真和实验表明了该法稳态测速误差小,动态实时性好,相比传统M法具有优越的性能。
[1] 林瑶瑶,仲崇权.永磁同步电机高精度转速测量技术研究[J].大连理工大学学报,2012,52(6):890-895.
[2] 鲁进军,梅志千,刘向红,等.电动机的高精度宽范围转速测 量 方 法[J].中 国 电 机 工 程 学 报,2011,31(24):118-123.
[3] Merry R,Molengraft R,Steinbuch M.Error Modeling and Improved Position Estimation for Optical Incremental Encoders by Means of Time Stamping[C]//American Control Conference,ACC2007.IEEE,2007:3570-3575.
[4] Zhang J,Yu J.A Novel Approach to Measuring Motor Speed[C]//Measurement,Information and Control(MIC),2012 International Conference on.IEEE,2012,1:248-251.
[5] 于兆凯.基于STM32的永磁同步电机伺服系统的研究[D].杭州:浙江大学,2012.
[6] 薛高飞,胡安.一种基于编码器的全阶观测器测速方法[J].海军工程大学学报,2013,25(6):1-6.
[7] Brown R H,Schneider S C,Mulligan M G.Analysis of Algorithms for Velocity Estimation From Discrete Position Versus Time Data[J].Industrial Electronics,IEEE Transactions on,1992,39(1):11-19.
[8] 王成元,夏加宽,孙宜标.现代电机控制技术[M].北京:机械工业出版社,2013.
[9] 张晓光,孙力,赵克.基于负载转矩滑模观测的永磁同步电机滑模控制[J].中国电机工程学报,2012,32(3):111-116+8.
[10]陈荣.永磁同步电机伺服系统研究[D].南京:南京航空航天大学,2005.

