基于自适应差分进化算法优化极限学习机的球磨机料位测量

王 芳，续欣莹，阎高伟

(太原理工大学信息工程学院，山西太原 030024)



基于自适应差分进化算法优化极限学习机的球磨机料位测量

王 芳，续欣莹，阎高伟

(太原理工大学信息工程学院，山西太原 030024)

极限学习机在实际应用中具有学习速度快、训练误差小的优点,但其稳定性与泛化能力却较差。针对其缺点，将自适应差分进化算法引入极限学习机对其改进,利用自适应差分进化算法的全局寻优能力，求取训练误差较小时极限学习机的输入权值矩阵以及隐含层偏置矩阵,从而优化极限学习机。将优化后的极限学习机应用于球磨机料位测量，实验结果表明，优化后的极限学习机与传统极限学习机相比具有较高的测量精度和较好的稳定性。

自适应差分进化算法；极限学习机；测试误差；球磨机料位测量

0 引言

针对球磨机的料位测量，学者们提出了各类方法。文献[1]引入支持向量机(SVM)并结合机理知识对球磨机料位进行软测量。文献[2]针对球磨机优化工况监测的不足，提出了基于筒体振动信号的球磨机优化工况监测方法。文献[3]基于振动信号和反向传播神经网络建立了球磨机料位的软测量模型。神经网络模型在球磨机的料位测量中具有一定的应用价值。然而传统神经网络模型的测量精度会因样本数量而受限。

极限学习机(Extreme Learning Machine，ELM)是由黄广斌等提出的单隐层前馈神经网络的学习算法，相比于传统的神经网络模型，具有学习速度快，训练误差小的优点。极限学习机有效避免了传统神经网络模型存在的网络结构难以确定和容易造成过学习的缺点[4-5]。然而，利用训练集进行学习时，ELM 的输入权值以及隐含层偏置矩阵均为随机生成，使得ELM 的稳定性与泛化能力较差。自适应差分进化算法(Self-adaptive Differential Algorithm,SaDE)[6]由A．K．Qin 等提出，是对传统差分进化算法的改进。与传统差分进化算法相比，SaDE具有更强的全局搜索能力、更快的收敛速度和更高的收敛精度。

综上，本文将SaDE引入极限学习机，利用SaDE的全局搜索能力获得与训练样本最佳匹配的输入权值矩阵以及隐含层偏置矩阵。文中将极限学习机对于给定样本集的训练误差作为SaDE的寻优函数，通过种群个体的不断进化获得训练误差较小时相应的种群个体，由此得到输入权值矩阵以及隐含层偏置矩阵，从而提高ELM的测量精度。之后，将自适应差分进化算法优化极限学习机方法用于球磨机料位测量，验证了该方法的有效性和实用性。

1 自适应差分进化算法优化极限学习机

1．1 极限学习机(ELM)

设训练集样本为[xi,yi](i=1,2,…,N,N为训练样本个数)，ELM的隐含层单元个数为k，激发函数为g(x)，则ELM的输出模型为

(1)

式中：βj为连接第j个隐含层节点和输出节点的权重；αj为连接第j个隐含层节点和输入节点的权重矩阵；dj为第j个隐层节点的偏置值；g(x)可选为sigmoid、sine或RBF等函数。

训练过程中，求取α、β、d满足如下等式：

(2)

式(2)可由矩阵表示为：

Hβ=Y

(3)

(4)

从而，隐含层和输出层之间的连接权值β可由极小2-范数最小二乘解得：

(5)

式中H†为隐含层输出矩阵H的Moore-Penrose广义逆。

综上所述，极限学习机的实现步骤为：

(1) 根据训练样本集[xi，yi](i=1,2,3…,N,N为训练样本个数)，确定激励函数g(x)以及隐含层单元个数k；

(2) 随机生成输入权值矩阵α以及隐含层偏置矩阵d;

(3) 根据式(4)求得隐含层输出矩阵H;

(4) 根据式(5)求出连接权重β。

1．2 自适应差分进化算法优化极限学习机

自适应差分进化算法(SaDE)是一种随机并行搜索算法，其实质为实数编码的贪婪遗传算法。与传统的差分进化算法[7-8]相比，该算法在种群进化过程的不同时期采取不同的变异策略，从而提高了算法的收敛速度与收敛精度。

自适应差分进化算法优化极限学习机(SaDE-ELM)实现步骤如下：

1.2.1 初始化

给定训练样本集[xi，yi](xi∈Rn，n为输入神经元个数，i=1,2,…，N,N为训练样本个数)，设置极限学习机隐含层单元个数k以及激励函数g(x)。初始化NP个维数为D(D=k·(n+1))的参数向量tr,g(r=1,2，…,NP)，编码方式为实数编码，g表示迭代次数，种群个体每一维的取值范围为[-1,1]。

其任意一个种群个体t由ELM的输入权值矩阵α(α1,α2,…αk)和隐含层偏置矩阵(d)组成，即t=[α11,α12…αln,…,αk1,αk2,…，αkn,d1,…，dk]。

对于每一个种群个体tr,g，按照式计算出隐含层输出矩阵H，然后按照式得到输出权重β，最后按照式计算每个个体的均方根误差(Root-Mean-Square Error,RMSE)。

(6)

1.2.2 变异

对于任意一个目标向量tr,g，取式(7)、式(8)两种变异策略中的一种进行变异操作。

νr,g+1=tr1,g+F·(tr2,g-tr3,g)

(7)

νr,g+1=tbest,g+F·(tr1,g-tr2,g)

(8)

式中：r1、r2、r3表示种群个体序号，三者互不相同，且分别与目标序号r不同，因此须满足NP≥4；tbest,g表示当前种群中适应度值最高的个体；变异概率F的取值范围为[0,1]。

式(7)变异策略收敛速度较慢，空间搜索能力很强。式(8)变异策略收敛速度较快，容易陷入局部最优。因此，在SaDE中，为了能够最大范围的覆盖搜索空间，算法运行初期按照式进行变异操作，而在算法运行后期需要以较快的速度收敛至最优值区域，按照式(8)进行变异操作。

1.2.3 交叉

交叉操作基于原始向量tr,g以及变异向量vr,g+1，按照式生成新的交叉向量ur,g+1。

μr,g+1=(μ1r,g+1,μ2r,g+1,…,uDr,g+1)

(9)

(r=1,2,…,NP；S=1,2,…,D)

式中：randb(0,1)产生第s维的随机数；randi(D)为1,2,…,D中的随机数，这样保证了试验向量ur,g+1的一部分信息是继承于个体vr,g+1；CR为交叉概率，取值范围为[0,1]。

1.2.4 选择

依据贪婪准则对比试验向量ur,g+1与当前种群中的目标向量tr,g的适应度值，保留适应度值较高的个体。在选择过程中将均方根误差(RMSE)作为适应度函数。SaDE-ELM的基本流程如图 1所示。

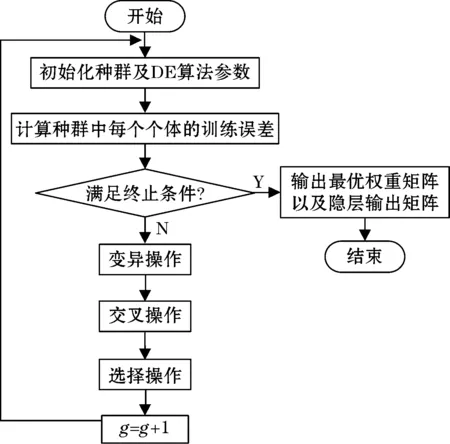
图1 SaDE-ELM流程图

2 SaDE-ELM用于球磨机料位测量

2．1 实验数据采集

实验中所用的样本数据来自对小型实验室球磨机的数据采集。该球磨机尺寸为Φ360 mm×450 mm，通过功率为2．2 kW的电动机对其驱动，球磨机转速设为60 r/min。球磨机滚筒内加入适量的钢球，物料每1 min增加1 L，期间以50 kHz 的采样频率采集每升料位下的振动信号。数据采集由数据采集系统完成，主要组成部分包括振动传感器、信号放大器、滤波电路以及USB数据采集器和上位机组成。具体的操作为将振动传感器置于球磨机远离电动机一端的轴承底座。

实验结束时，共采集得到20组数据，分别为料位由1L增至20L球磨机的振动信号，经过预处理每个料位下将得到22个表征其料位属性的样本数据，所以共有20×22=440组数据样本，每组数据为30维，选取其中300个样本作为训练集，剩下的140个样本作为测试集。因此SaDE-ELM模型的训练集规模为300×30，测试集规模为140×30。

2．2 实验结果分析与对比

为了验证SaDE-ELM模型的有效性，将其与传统的ELM进行比较。模型的输入为球磨机振动信号特征，输出为球磨机料位预测值。采用均方根误差(RMSE)对预测效果进行评价。

实验中SaDE的参数设置为：CR=0．8，F=1，tolerance=0.02，种群个数NP=30，算法的最大迭代次数为iter=20。为了节约运行时间，减小计算复杂度，隐含层单元个数k=20。考虑到ELM 自身的不稳定性，两种方法分别运行10次，最后求取平均RMSE来评价测量精确度。所得到的平均RMSE和测量曲线如表 1和图 2所示。

表1 球磨机料位测量结果对比

(a)SaDE-ELM测量结果

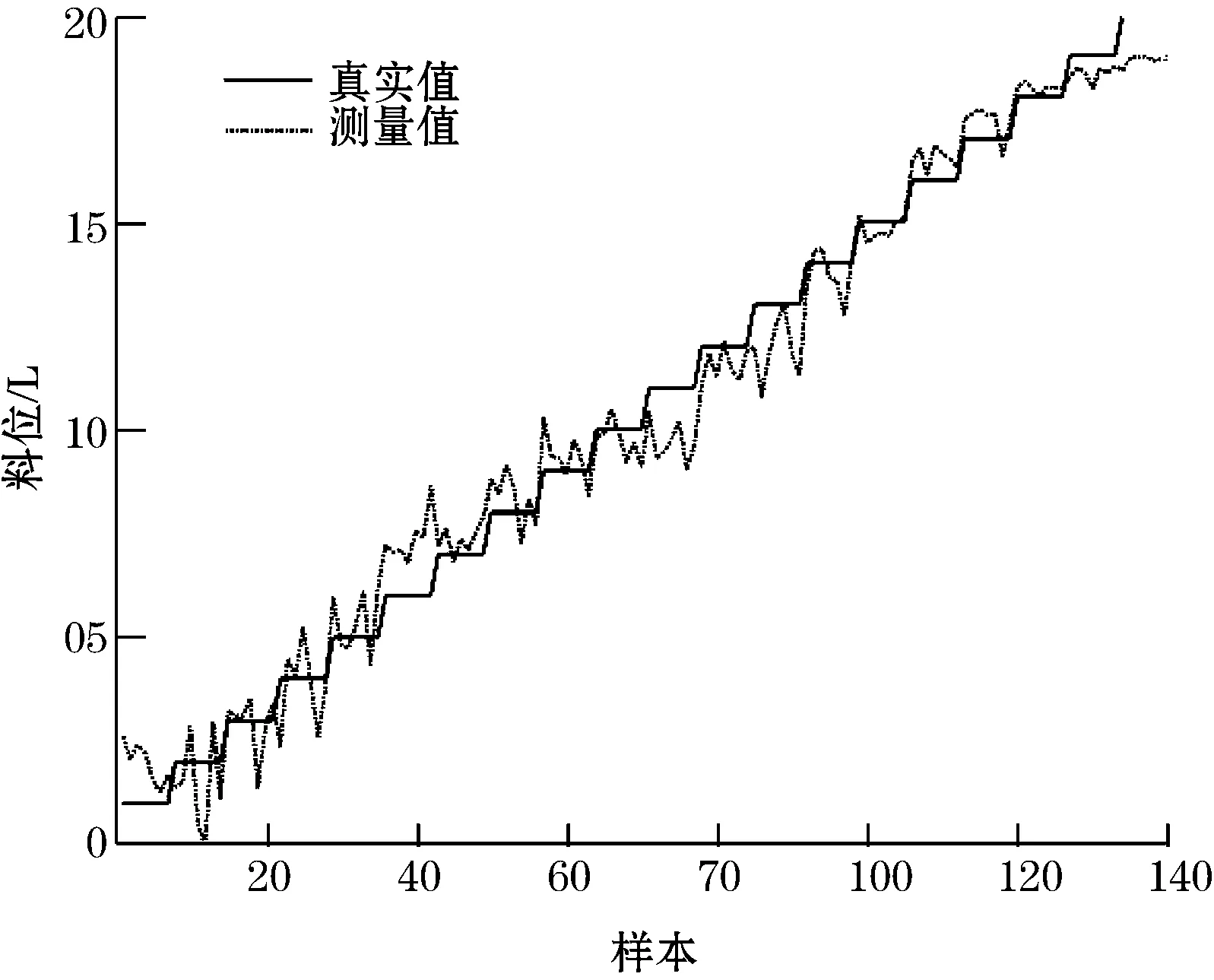
(b)ELM测量结果图2 测量结果曲线图

由表1可看出，无论是测试误差还是训练误差，SaDE-ELM所得结果均小于ELM，因此SaDE-ELM模型的学习能力以及泛化能力均优于ELM。

图2中横轴表示测试集采样序列，纵轴表示料位值。由图 2测量结果曲线图可看出SaDE-ELM无论是在低料位段还是在高料位段，其跟踪效果与ELM相比均有明显优势，测量精度大幅度提高，验证了SaDE-ELM方法的有效性与优越性。

其原因为在ELM算法中，输入层和隐含层之间的连接权值矩阵(a)与隐含层的偏置向量(d)为随机选取，在提高ELM本身的学习速度的同时却牺牲了算法的测量精度。矩阵a、d的随机选取使得对于训练样本的学习在一定程度上缺乏针对性。而SaDE-LEM利用差分进化算法的全局寻优能力找到与训练样本较为匹配的矩阵a、d，减小了测试误差。

为了分析SaDE-ELM 算法的稳定性，将10次测量结果通过箱线图表示为图 3。由图 3可以看出，ELM的稳定性较SaDE-ELM差，其原因为ELM模型初始化的随机性导致其稳定性较差。

综上所述，SaDE-ELM不仅具有较高的测量精度，而且其稳定性相对于ELM有很好的改善。

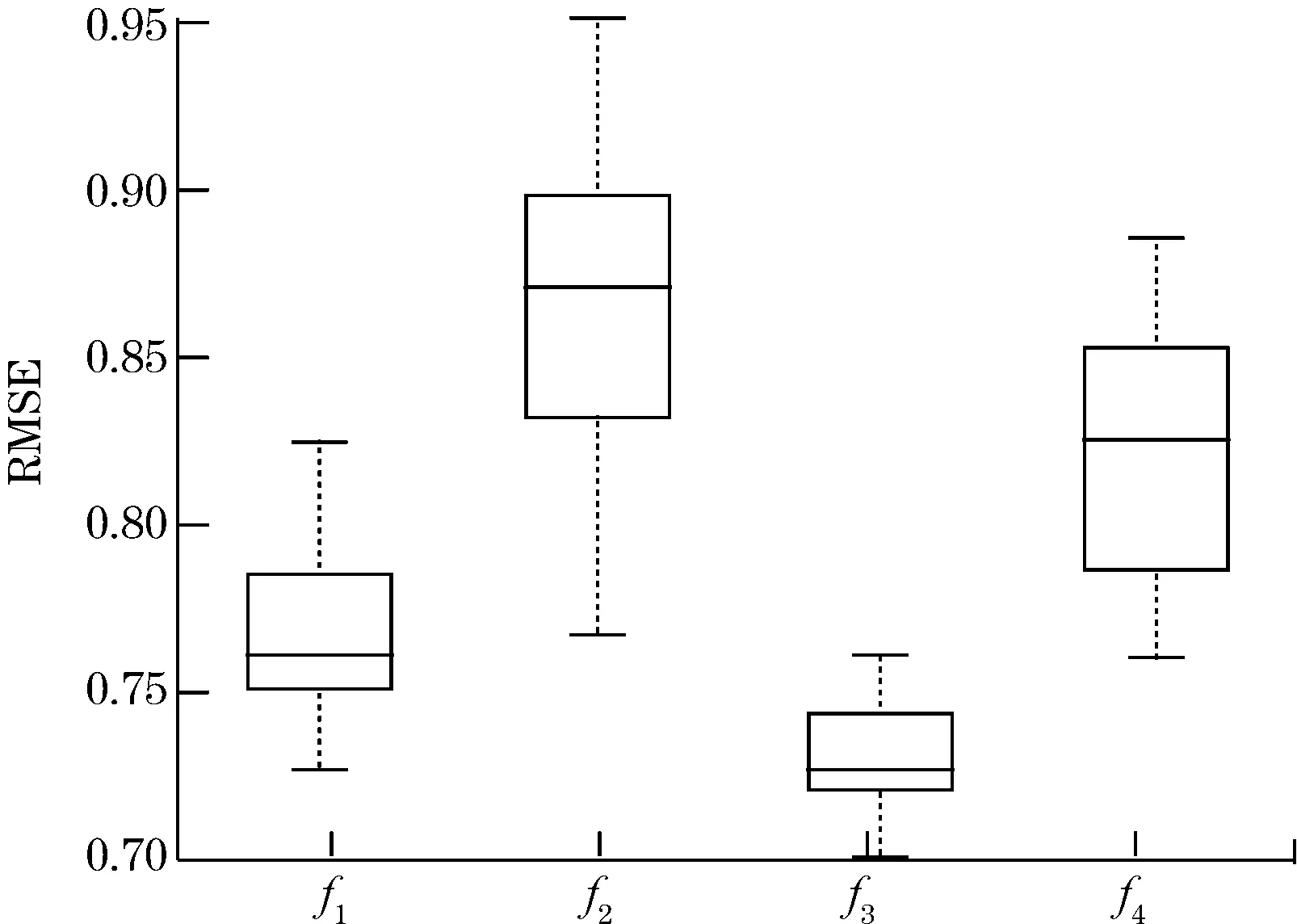
f1：SaDE-ELM测试误差 f2：ELM测试误差f3：SaDE-ELM训练误差 f4：ELM训练误差图3 10次测量结果的箱线图

3 结论

利用自适应差分进化算法较强的全局寻优能力优化极限学习机(ELM)，从而提高其学习能力与泛化能力。将优化后的极限学习机算法(SaDE-ELM)应用于球磨机料位测量，实验表明，自适应差分进化算法极限学习机的训练精度与测试精度都优于极限学习机，同时SaDE-ELM在稳定性方面也有提高。

[1] 王恒,贾民平,陈左亮．基于LS-SVM和机理模型的球磨机料位软测．电力自动化设备,2010,30(7)：92-95．

[2] 王恒,贾民平,黄鹏,等．基于筒体振动信号的球磨机优化工况检测 ．仪表技术与传感器,2012(11)：145-148．

[3] 汤健,郑秀萍,赵立杰,等．基于频域特征提取与信息融合的磨机负荷软测量．仪器仪表学报,2010,31(10)：2161-2167．

[4] HUANG G B,ZHU Q Y,SIEW C K．Extreme learning machine：theory and applications．Neurocomputing,2006,70(1)：489-501．

[5] HUANG G B,ZHU Q Y,SIEW C K．Real-lime learning capability of neural networks．Singapore：School of Electrical and Electronic Engineering,Nanyang Technological University,2003．

[6] QIN A K,HUANG V L,SUGATHAN P N.Differential evolution algorithm with strategy adaptation for global numerical optimization．IEEE Transactions on Evolutionary Computation,2009,13(2)：398-417．

[7] STORN R,PRICE K．Differential Evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces．International Computer Science Institute,1995(8)：222-225．

[8] KAELO P,ALIM M．A numerical study of some modified differential evolution algorithms ．European Journal of Operational Research,2006,169(3)：1176-1184．

Measurement of Ball Mill Material Level Based on Self-adaptiveDifferential Algorithm and Extreme Learning Machine

WANG Fang,XU Xin-ying,YAN Gao-wei

(College of Information Engineering,Taiyuan University of Technology,Taiyuan 030024，China)

The advantages of extreme learning machine has strong learning capacity and smaller training deviation．To further improve the reliability and decreasing the test deviation of extreme learning machine,self-adaptive differential algorithm was introduced to extreme learning machine．Then smaller test deviation of sample sets was acquired in this way．Lastly,optimized extreme learning machine was applied to measure the ball mill material level．The experiment result shows that the test deviation and training deviation of this method are largely smaller than that of extreme learning machine．At the same time,learning capacity and generalization performance of this method are also better than that of original extreme learning machine．

self-adaptive differential algorithm；extreme learning machine；test training deviation；ball mill material level

项亚南(1989—)，硕士研究生，主要研究领域为检测技术及自动化装置。E-mail：xiangyanan1989@foxmail．com 潘丰(1963—)，教授，博士生导师，主要研究领域为生产过程优化控制等研究。E-mail：pan_feng_63@163．com

国家自然科学基金项目(60975032)；山西省自然科学基金项目(2011011012-2)

2014-07-03 收修改稿日期：2015-03-10

TP29

A

1002-1841(2015)06-0143-03