压缩感知中一种改进内点算法的研究
董 腾,杨 帆,潘国峰
(1.中国人民解放军93704部队,北京 101100;2.河北工业大学信息工程学院,天津 300401)
压缩感知中一种改进内点算法的研究
董 腾1,2,杨 帆2,潘国峰2
(1.中国人民解放军93704部队,北京 101100;2.河北工业大学信息工程学院,天津 300401)
提出一种基于内点法的改进重构算法,尝试用专门的内点算法解决稀疏重构问题。首先,在内点法基础上引入预处理算子重新设计来避免牛顿方程系统的构造,使矩阵拥有良好的可调性;其次,利用稀疏矩阵的矩阵特性简化矩阵矢量增量。仿真实验结果表明改进的内点算法对实际问题的处理是有效且优于其他算法的。
压缩感知;内点法;稀疏矩阵;预处理;共轭梯度
0 引言
压缩感知[1-3](Compressed Sensing,CS)理论是21世纪初提出的一种全新的信息获取理论。该理论的提出能够有效应对目前大信息量数据传输和存储成本极高的问题,因此理论一经提出便引起国内外相关学者的广泛关注,基于压缩感知的数据重构理论、算法不断被提出。
基于压缩感知理论的重构算法包括凸优化算法、方向寻优算法和贪婪算法等[4]。凸优化类算法通过凸优化问题的极小化算法以极大概率逼近目标函数以此重构出原始信号,此类算法所需观测次数少,重构精度高,但计算复杂度高。目前主要有内点法、基追踪(BP)法和迭代阈值法等。
本文利用内点算法[5]原始对偶特性,引入预处理共轭梯度对内点法加以改进,降低了算法复杂度,提高了算法的效率,在处理稀疏重构尤其是大规模重构问题时达到较好的重构效果。目前,较先进的重构算法有定点连续有效集法(FPC-AS)[6]和光谱投影梯度(SPGL1)算法[7],PDCO算法[8]是另外一种基于内点算法的改进算法,在文中利用这三种算法作为本文算法的比较算子,来比较改进算法的计算效率。
1 压缩感知的基本问题
压缩感知基本问题为求不完备线性方程的解(m (1) 研究表明,在某些场合中x稀疏解的精确重构问题可以极大概率通过求解下列基追踪[9]问题得到解决: (2) 在实际应用中,式(1)右边经常会有噪声干扰,因此表示为 (3) 式中e为误差,e∈Rm。 (4) 式中τ为调节稀疏度和噪声误差上限的正标量。 式(4)就是著名的基追踪降噪法。实际问题总是具有较大的规模,现成的办法使得如单纯形法或内点法无法实现。然而,在压缩感知问题中出现的矩阵A展示出了良好的特点,在优化算法中可以加以利用。基于此本文提出一种专门的方法来解决这个问题。 定义新变量u和ν∈Rn,则有 |xi|=ui+vi,∀i=1,2,…,n (5) ui=max(xi,0),νi=max(-xi,0)。则1范数形式变为 (6) u,ν≥0,ln∈Rn成为一个列向量。用上述线性方法,解决式(4)中的约束光滑重构: (7) 式中:z=[u;ν]∈R2n;FT=[A,-A]∈Rm×2n。 一旦变量u和ν最优解被找到,那么x的初始值就可通过计算下式得到: x=u-v 线性化的意义在于初始化式(4)的维数是双数,有2n个非负的约束条件加入。通过加入约束条件z≥0,使得线性搜索的每一步沿着负梯度方向并且新的迭代被投影到可行域。 2.1 内点法的原始对偶问题 非光滑基追踪式(2)和基追踪去噪式(4)最优化问题可以重新分别表示为等效线性和二次凸规划问题。这些通过对目标函数非光滑1范数规范化而得到。 对于原始问题式(7),它的对偶: (8) z,s≥0 在每一步原始对偶内点法[5]应用原始对偶对式(7)和式(8),相应牛顿方向(Δz,Δs)的计算通过下边系统的线性方程来解决: (9) 式中:S和Z是s和z在对角线上的对角阵;I2n表示2n阶的单位阵。 (10) 式中:μ=z′ts/(2n)是内点法的约束项;σ为定心参数,0≤σ≤1。 在稀疏矩阵结构中,式(9)中的对偶变量Δs被除去,得到: (Θ-1+FFT)Δz=fz+Z-1fs (11) Δs=Z-1fs-Θ-1Δz (12) 式中Θ=S-1Z∈R2n×2n。 简化的牛顿系统式(11)又称增广系统,可由只有约束矩阵F存在的预处理迭代法处理。 2.2 预处理共轭梯度法解决原对偶问题 式(11)有一个对称正定矩阵,在稀疏矩阵中可用共轭梯度(CG)法[10]来处理。可是当矩阵是病态或特征值不集中时,CG法的收敛性很慢。在本节,讨论一种有效的等量对角矩阵调节器来解式(11)的问题。 式(11)里提出的预调节器是利用式(11)CS矩阵一般特性和Θ矩阵的近似最优解的通用属性的。在式(7)、式(8)中原始对偶对的符号表示,变量s∈R2n是一个非负性约束z≥0的拉格朗日乘数。因此,在最优解处sjzj=0(j=1,2,…,2n)。内点法通过微扰这个约束条件sjzj=μ使收敛向着最优解,μ是内点法的约束项,使μ逐渐减少扰动直至0。在最优值j∈{1,2,…,2n}处,被分解为2部分: (13) 这决定了约束条件的约束能力。这种分割对对角缩放矩阵Θ=S-1Z产生极大的不良影响:当μ趋向于0时,指数j∈Β,Θj趋向无穷大,j∈Ν,Θj趋向于0。 前面提到z=[u;v],u,v分别是向量x的正负部分。对于稀疏信号,只有k(k≪2n)的非零部分是最优解。u中将提供一个正的非零解,v将提供一个负的非零解。在Β中最优解是k。因此,内点法的后期迭代为 (14) 回到式(12)提出的预处理问题,它的矩阵为 H=Θ-1+FFT (15) 矩阵Θ近似最优解由式(14)表示。矩阵Θ-1有许多项,在内点法达到最优解[11]之前只有很少部分是完备解。设一个数C≫1将Θ-1分解成不同部分: (16) l只是Θ-1里少数项的数目,与最优解中的稀疏的k不同。在l (17) 预调节器是基于ATA的近似,近似由封闭的扩展单位阵ρIn得到,ρ=m/n: (18) 为了简化对这个预调节器的分析,首先考虑n×n的矩阵H和P而不是式(17)、式(18)中所说的2n×2n的形式。下边的引理建立了预处理矩阵P-1H在不分块部分的频谱特性: 引理1定义矩阵H: H=Θ-1+ATA 式中:Θ=diag(Θ1,Θ2,…,Θn);Θ为n×n对角线阵Θj>0;A为m×n矩阵,m≤n/2。 P=Θ-1+ρIn,ρ=m/n 在1处收敛,也就是说: (19) 如果矩阵A有近似正交行,可得: 描述式(11)中预处理矩阵P-1H的频谱特性。使式(17)、式(18)中的H,P为分块矩阵,则预处理矩阵P-1H有:n的多重特征值为1;其余n的特征值由引理1中Θ=Θu+Θv来定义。得到了P-1H在1附近收敛的特征值。因此,最终目的是希望应用于式(11)的共轭梯度法的迭代在使用式(18)的预处理算子P时可以尽量少。在式(17)中H的矩阵A特征值λ(H)和λ(P-1H)的聚集是一个有标准正交行的离散余弦变换(DCT)矩阵,AAT=I。设数据规模为m=210,n=212,稀疏度k=51。得到如图1所示特征值收敛分布。在图1(a)中,显示特征值λ(H)的聚集性。每一条垂线显示特征值λ(H)在稀疏矩阵内点法共轭梯度调用中的分布变化趋势。可以看到点的聚集性随着稀疏矩阵内点法的优化而变坏,而预处理矩阵P-1H特征值却正相反,如图1(b)。尤其是随着稀疏矩阵内点法的推进特征值λ(P-1H)开始在1附近收敛[12-13]。 图1 矩阵H和P-1H特征值的收敛性 2.3 改进的内点算法 迭代法(预处理共轭梯度法)处理式(11)、式(12),在计算复合方向每一项时是近似相同的。为了避免过度计算,在每次迭代之前校正方向,稍稍偏离预测器指向中央的方向而只在必要时按照校正器指向方向。如同原对偶内点法中长变量一样,这保证了每一次迭代目标函数迅速减少而算法保持指向中心的路径尽量小。当许多有误差的预测方向被执行了,那么原对偶迭代开始向着可行域的边界靠近。这导致了连续迭代的步长变小。当这种情况发生时,一个强有力的向心校正器开始发挥作用,使下一步迭代向着中心附近保证下一步迭代取值足够大。理论上,原对偶方向步长值要远离0以使全局收敛得到保证。这使得原对偶内点法只需少量的迭代就能够快速收敛。 改进内点算法(计为C-IPM)流程如下: 对于k=1,2,…有从zk到zk+1和从sk到sk+1的迭代: While式(7)and式(8)对偶间隙≥εdo σ=σ2 elseσ=σ1 end if (预测器) (校正器) σ=σ3 end if end while。 将通过仿真实验分析本文所提算法的性能,验证改进算法在计算时间、重构效率上与现有先进算法的优势。所有实验都在MATLAB中运行调试。都使用MATLAB R2010b 64-bit在CORE i7 下的win7系统中运行。 表1是一维稀疏信号的重构试验结果对比,选择(n/2)×n形式的矩阵,信号长度n变化从500到30 000,稀疏度k=51,通过不同算法得到的运行时间的对比图如表1所示。将本文所提改进算法记为C-IPM法。实验表明,算法的运行时间在矩阵规模在2 500×5 000以下时,本文所提改进算法与现有先进算法和基于内点算法的其他算法相比,所用时间优势相当明显,对比从500~30 000各实验采集点可发现矩阵规模在5 000以内时,改进算法的计算效率至少提高1倍以上,当矩阵规模逐渐增大,这种优势变得越来越明显,计算效率相比其他算法有了较大优势,甚至PDCO算法已经在现有硬件条件下无法计算出结果,说明了本算法在处理大规模重构问题时效果非常理想,对于目前数据信息采集和传输规模越来越大的实际困难,利用改进内点算法处理大规模、超大规模重构问题有很大的现实意义。 表1 不同算法计算效率对比 图2是不同噪声干扰下一维稀疏信号的重构实验,信号长度n=500,稀疏度k=51,分别加入噪声均方差为0、0.01、0.03、0.05的高斯白噪声对信号进行测量,相应的重构结果如图2(a)一图2(d)所示。由图2实验结果可以看出,在噪声均方差低于0.05的不同程度噪声干扰下,改进内点算法可精确重构出原始信号。 图3比较了本文所提的改进算法与原始数据相变特性,参数n固定为1 000。测量值m变量范围100~900。对每9个测量值m最优表示的稀疏度k变化从1至m,对于每个k,都进行100次实验。由图3可以看出改进内点法实验相变特性与理论上的平均相变特性曲线相重叠,说明本文所提改进算法在重构质量上达到了完全重构。 本文设计并提出了一种低复杂度的稀疏矩阵原对偶内点法来解决压缩感知领域提出的l1正规化问题。在原始对偶内点法每次迭代中,迭代方向由共轭梯度法解线性系统得到。然而矩阵Θ-1+FFT作为算法收敛是一个病态的,因此,共轭梯度法计算缓慢。为了解决这一病态问题,本文为共轭梯度法设计出一个低成本的预调节器。数值实验证实了改进算法在计算效率上有了明显的提升,为解决大规模信息处理问题提供了一种新的尝试。 (a)稀疏随机阵(噪声均方差:0) (b)稀疏随机阵(噪声均方差:0.01) (c)稀疏随机阵(噪声均方差:0.03) (d)稀疏随机阵(噪声均方差:0.05)图2 不同噪声干扰下一维稀疏信号的重钩 图3 原始数据与改进算法相变特性比较 [1] 张波,刘郁林,王开.稀疏随机有限等距性质分析.电子与信息学报,2014,36(1):169-174. [2] 宁方立,何碧静,韦娟.基于lp范数的压缩感知图像重建算法研究. 物理学报,2013(17):174-212. [3] SUN H, YUAN H M, LU S M. A design of three-phase digital watt-hour power meter on SOPC platform.Proc. of International Conference on Information Technology and Computer Science:IEEE Press, 2009. [4] 李珅,马彩文,李艳,等.压缩感知重构算法综述.红外与激光工程,2013,42(S1):225-232. [5] 雍龙泉.线性规划的原-对偶内点算法数值实验初步.科学技术与工程,2007,7(18):4576-4579. [6] WEN Z, YIN W, GOLDFARB D, et al. A fast algorithm for sparse reconstruction based on shrinkage, subspace optimization and continuation.Sci. Comput.32(4):1809-1831, 2010. [7] BERG E V, FRIEDLANDER M P. Probing the Pareto frontier for basis pursuit solutions. SIAM Journal of Scientic Computing,2008,31(2):890-912. [8] SAUNDERS M, KIM B. PDCO:Primal-dual interior method for convex objectives.Technical Report, Stanford University, 2002. http://www.stanford.edu/group/SOL/software/pdco.html. [9] CHEN S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit.SIAM Journal on Scientic Computing, 20(1):33-61, 1998. [10] 董晓亮,李郴良,唐清肝.一类Wolfe搜索下的共轭梯度法及其全局收敛性.广西科学,2007,14(1):44-46. [11] 姜志侠,李军,张珊.一个改进的原始对偶内点法.吉林大学学报,2009,47(4):677-682. [12] HAUPT J, BAJWA W, RAZ G, et al. Toepitz compressed sensing matrices with applications to sparse channel estimation.IEEE Transactions Information Theory, 2010, 56(11):5862-5875. [13] LIU Y L, WANG K,HE J W. Signal recovery by compressed sensing in IR-UWB systems. Chinese Journal of Electronics, 2012, 21(2):339-344. Algorithm for Modified Interior Point Methods on Compressed Sensing DONG Teng1,2,YANG Fan2,PAN Guo-feng2 (1.The 93704 Unit of the Chinese People’s Liberation Army,Beijing 101100,China;2.School of Information Engineering,Hebei University of Technology,Tianjin 300401,China) To use a special interior point method solve the sparse reconstruction problem,a modified reconstructed method based on interior point method was proposed.First,to avoid construction of Newton equations system,a preconditioning operator was lead up which was based on the interior point method to make the matrix have good adjustability.Second,the characteristics of sparse matrix were used to simplify the matrix-vector incrementing.The experimental results show that the modified interior point method is effective and better than any other algorithms for practical problems. compressed sensing;interior point method;sparse matrix;precondition;conjugate gradient 国家科技重大专项资助项目(2009ZX02308-004) 2014-07-30 收修改稿日期:2015-03-28 TP391 A 1002-1841(2015)06-0138-05 董腾(1987—),硕士研究生,助理工程师,主要从事图像处理、智能信息处理及信号分析等方面的研究。 E-mail:dongteng2006@sina.com 杨帆(1964—),博士,教授,博士生导师,主要从事计算机视觉检测技术、生物特征识别技术和图像处理与模式识别方面的研究。
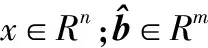




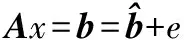

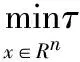
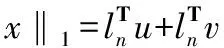
2 内点算法的改进研究
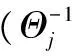

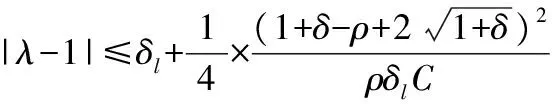
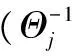





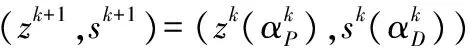

3 仿真实验

4 结束语






