MCMC粒子滤波和复化Newton-cotes算法测算区域面积的方法

王志超，曹起武，张 全

(1.沈阳工业大学信息学院，辽宁沈阳 110870；2.辽宁机电职业技术学院信息系，辽宁丹东 118009)



MCMC粒子滤波和复化Newton-cotes算法测算区域面积的方法

王志超1，曹起武2，张 全1

(1.沈阳工业大学信息学院，辽宁沈阳 110870；2.辽宁机电职业技术学院信息系，辽宁丹东 118009)

针对不规则区域面积测算中定位精度和面积计算精度两方面不足，提出一种定位精度高、面积误差小的面积测算新方法。其采用一种组合定位方法精确定位，即将差分GPS测量系统(DGPS)与马尔可夫链蒙特卡罗(Markov chain Monte Carol，MCMC)粒子滤波相结合，再配合复化Newton-cotes算法，拟合边界曲线并准确求得区域面积。将MCMC粒子滤波应用于DGPS定位数据处理，其既可处理非高斯分布噪声，又解决粒子滤波(PF)的粒子退化问题，提高定位精度。将复化Newton-cotes算法应用于面积计算，其既避免高次插值的舍入误差，又将面积区间进一步细分，提高面积计算精度。实验结果表明，该新方法定位精度更高，面积误差更小。

不规则区域；面积测算方法；差分GPS测量系统；马尔可夫链蒙特卡罗；粒子滤波；复化Newton-cotes算法

0 引言

借助GPS 测算不规则区域面积的方法研究既是当今物联网的一个具体应用，又是智能控制理论研究的课题之一[1-2]。GPS已经在林业面积估算、农业土地面积测量以及城市规划等不规则区域面积测量方面得到了越来越广泛的应用[3]。然而，一些测量不规则区域面积的传统方法存在定位精度低、速度慢、面积计算误差大等诸多问题[4]。以传统方格法和数字电子地图法为例，主要存在以下缺陷：

(1)环境干扰导致定位不准确[5]；

(2)直线代替曲线导致边界拟合误差大[6]；

(3)面积求算方法误差大[7]。

综上，提出一种不规则区域面积测算的新方法，其能较快速且准确地测算不规则区域的面积。

首先介绍了C/A伪码差分GPS测量系统(DGPS)，并引用马尔可夫链蒙特卡罗移动步骤(Markov Chain Monte Carlo，MCMC )对粒子滤波(Particle filter，PF)进行改进，提出DGPS与MCMC粒子滤波相结合的组合定位方法；随后详细介绍并推导复化牛顿-柯特斯算法(Compound Newton-cotes algorithm)，并给出其与改进方格法相结合求被测区域面积的详细过程描述；最后分别对两种算法进行实验验证，给出实验结果。仿真结果表明：与传统不规则区域面积测量方法相比，DGPS与MCMC粒子滤波组合定位能大幅提高GPS坐标定位精度，复化牛顿-柯特斯求积算法能提高求积精度。该方法是一种定位精度更高，计算误差更小，抗干扰性更强的不规则区域面积测量新方法。

1 DGPS与MCMC粒子滤波组合定位

1.1 C/A伪码DGPS定位

由于大气条件等不定因素影响，大多单机GPS定位精度只能达到±10 m级的水平[8-9]，如此精度测量较小面积显然无精度可言。故通常采用C/A伪码差分GPS测量系统(DGPS)提高定位精度[10]。DGPS可根据基准站已知位置信息，计算伪距中误差修正值，实时修正定位数据，有效消除常值误差。但其差分精度随基准站到用户的距离增加而降低，而这种误差是用任何差分法都不能消除的[11-12]。因此，采用DGPS与MCMC粒子滤波组合定位的方法来尽可能消除该误差。

1.2 MCMC粒子滤波

粒子滤波是基于贝叶斯估计的滤波方法，其基本思想是：由系统状态向量经验条件分布，在其状态空间中产生一组随机样本(即粒子)，随后由观测量情况不断调整粒子的位置和权重，根据调整后粒子信息，修正最初经验条件分布，如果有足够多的粒子，则经修正后的经验条件分布将收敛于系统状态向量的真实条件分布，此时，系统状态向量的估计值就可由这些粒子的均值得到[13]。

通常GPS动态定位的观测方程均为非线性的，为使定位数据平滑输出，提高数据精度，常用卡尔曼滤波等滤波方法[14]。然而，这些滤波方法要求动力学模型噪声和观测噪声为独立不相关的高斯白噪声，且要求观测模型和动力学模型为线性模型，而线性化过程会引入舍入误差[15]，因此这些滤波算法不具备最优性。而粒子滤波(PF)算法可弥补该不足，其无须对观测模型线性化处理，且不要求动力学模型噪声和观测噪声为高斯白噪声，而直接通过蒙特卡罗模拟方法递推贝叶斯滤波，因此可用于由非线性观测模型表示的动态滤波系统[16]。

但PF经多次迭代后，易出现粒子退化现象[17]，它使粒子丧失多样性，导致采样枯竭，降低算法性能。为解决该问题，在PF重采样后引入马尔可夫链蒙特卡罗移动步骤，增加粒子的多样性，提高算法的性能[18]。仿真结果表明：MCMC粒子滤波能有效提高GPS动态定位的精度，其滤波效果优于一般PF和UKF等滤波算法[19]。

1.3 MCMC粒子滤波算法描述

设动态滤波系统的状态方程和观测方程可描述为

(1)

式中：Xk为状态向量;fk为状态转移函数;hk为观测向量和状态向量间的传递函数;Zk为测量向量;nk为观测噪声;υk-1为系统噪声[20]。

设第k-1时刻有一组后验粒子集{xk-1(i),ωk-1(i);i=1,2,…,N}，其中粒子数为N，xk-1(i) 表示第k-1时刻第i个粒子，ωk-k-1(i)表示第k-1时刻第i个粒子的权重。

(1)初始化粒子集，令k=0:

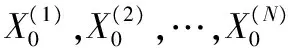
(2)当k=1,2,…时，执行以下步骤：

①状态预测

根据系统的状态方程计算p(Xk|Xk-1)，由计算得到的概率密度p(Xk|Xk-1)抽取第时刻的先验粒子：{Xk|k-1(i);i=1,2…,N}～P(Xk|Xk-1)。

(2)

归一化权值为

(3)

(4)

(c)估计

计算系统此时的状态估计值：

(5)

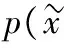
(1)在区间上以均匀概率抽样得门限值u,u～U[0，1]。

(2)由重要性概率密度函数p(xk|xk-1(i))抽样得xk|k-1(i),即xk|k-1(i)～p(xk|xk-1)。

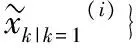
1.4 MCMC粒子滤波处理GPS定位数据算法描述

将上述MCMC粒子滤波应用于GPS定位数据的处理算法描述如下：

1.4.1 初始化粒子集，k=0

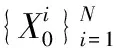
1.4.2 Fork=1,2,…循环执行以下步骤

(1)根据系统状态方程抽取第k时刻的先验粒子{Xk|k-1(i):i=1,2,…,N}～p(Xk|Xk-1)。

(2)更新

①更新权值：测量结束后，由系统的观测方程及式(6)计算粒子权值ωk(i)：

ωk(i)=ωk-1(i)p(Zk|Xk(i))i=1,…,N

(6)

将权值归一化为

(7)

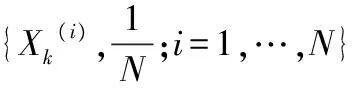
(3)估算此刻系统状态估计值:

1.5 组合定位

综上所述，MCMC粒子滤波在消除系统随机误差，保证动态性能的前提下，减小GPS定位数据的误差；而DGPS技术可有效消除电离层折射等常值误差[24]。若将这2种技术组合起来，既可减少由非正确预测引起的随机误差，又可减少在GPS定位时所产生的常值误差，从而大大提高GPS定位精度。实验证明：使用单机定位的精度误差为2.2 m (2σ)，而2种技术组合使用后其定位误差减少到0.8 m(2σ)以内[25]。

2 复化Newton-cotes算法

2.1 算法推导

本方法采用复化Newton-cotes算法计算区域面积。其基本思想是通过复化公式等分目标区间，并在每一个小区间内均使用一次Newton-cotes算法，即通过插值法用一个简单且易于积分的函数逼近目标函数fi(x),以计算积分I(fi),最终将每份面积I(fi)加和得到该区域面积I(f)。该算法通过复化公式降低插值阶数，从而减小舍入误差，同时又将目标区间进一步细化，精化计算面积。

(1)插值法求拟合曲线方程：由n次插值多项式：

(8)

拟合函数f(x)。

由f(x)≈Ln(x)，得

(9)

(2)Newton-cotes公式：采用等距节点情形的Newton-cotes算法。构造插值型求积公式：

(10)

对比式(9)，得

(11)

(12)

则当n=4时，式(10)可化为

(13)

式(13)即为柯特斯公式，它具有5次代数精度。

由式(12)可推出：当n增加到8以上时出现负系数，这会增大舍入误差，从而无法保证收敛性和稳定性。故采用高次插值不仅计算复杂，且易出现龙格现象，因此在实际计算中不能用高阶的Newton-cotes公式[26]。为在算法上进一步提高面积计算精度，则需要加密求积节点，但由上述问题不能无限制提高求积公式的阶数。故最终在Newton-cotes公式中引用复化公式，其既避免了由高次插值带来的舍入误差，又达到了对面积区间进一步细分的目的，从而大幅提高了面积的计算精度。

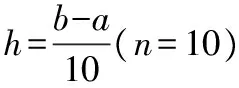
(14)

2.2 算法描述

复化Newton-cotes算法描述如下：

(1)拟合未知曲线：输入节点初值x0,x1,…,xn及其对应的函数值f(xk)(k=0,1,…,n)，由插值公式(8)求得未知曲线拟合方程F(x)。

(3)计算面积：由式(14)计算未知区域面积。

3 不规则区域面积测算新方法

综上，结合上述两方法各自优点，将传统方格法进行改进，提出不规则区域面积测算新方法：

(1)先由C/A伪码差分系统(DGPS)获得被测区域的边界坐标，随后配合MCMC粒子滤波算法平滑滤波输出，进一步提高定位坐标精度，在满足定位精度的条件下可将被测区域边界以间隔为1 m的点描标记出来，并分别找出上、下、左、右四个方向的极值点，以确定该不规则区域所在的最小外接矩形，如图1下半部分不规则区域外接矩形所示。

图1 分割、拟合方法示意图

(2)随后，在确定划分方格的大小时，为了便于使用复化Newton-cotes算法，这里采用大小为40 m×40 m的小方格将该外接矩形坐标平面分割为若干等大的小方格，如图1下半部分划分的小方格所示。

(3)接下来要使用改进的方格法对区域面积进行计算。通过上述划分方法，可以得到与被测区域无重叠、部分重叠和完全重叠这三类小方格。其中，与被测区域无重叠的方格在计算面积时不予考虑；与被测区域完全重叠的M个方格其重叠面积已知，记为S=1 600 m2；而对于那些与被测区域部分重叠的N个方格，要分别使用复化Newton-cotes算法进行面积计算：边界曲线f(x)如图1上半部分所示，先将该方格某边按等间隔细分10份，再分别于每一份小区间中使用一次Newton-cotes公式(即再次细分4份，此时该方格相当于被细分为40份，每个分割节点间距为1 m，符合上述坐标定位精度)，最终可由复化Newton-cotes公式求得与区域重叠面积大小，记为Si，如图1上半部分中，边界曲线f(x)与坐标轴所围面积。

4 实验与仿真

4.1 MCMC粒子滤波算法MATLAB仿真

4.1.1 仿真参数设定

为验证MCMC粒子滤波优于UKF、PF等传统滤波算法，对同一状态模型分别采用UKF、PF和MCMC粒子滤波算法进行比较。MATLAB仿真参数取值：时间步长T取5 s，采样间隔取τ= 1 s，滤波时间取50 s，粒子滤波的粒子数取500。 模型的状态初值x0=0.1,初始状态估计值：Xu=Xpf=Xmc=1,初始估计方差值：Pu=Ppf=Pmc=5 。设过程系统噪声和观测噪声均为白噪声，则过程系统噪声均方差：Vu=Vpf=Vmc=1,观测噪声均方差：Nu=Npf=Nmc=0.1。

4.1.2 仿真结果

通过MCMC粒子滤波算法得到的状态估计值与真实值关系如图2所示。由图2可以看出，经MCMC粒子滤波算法滤波得到的估计值均分布在真实值的95%置信区间之中，且其很接近真实值。

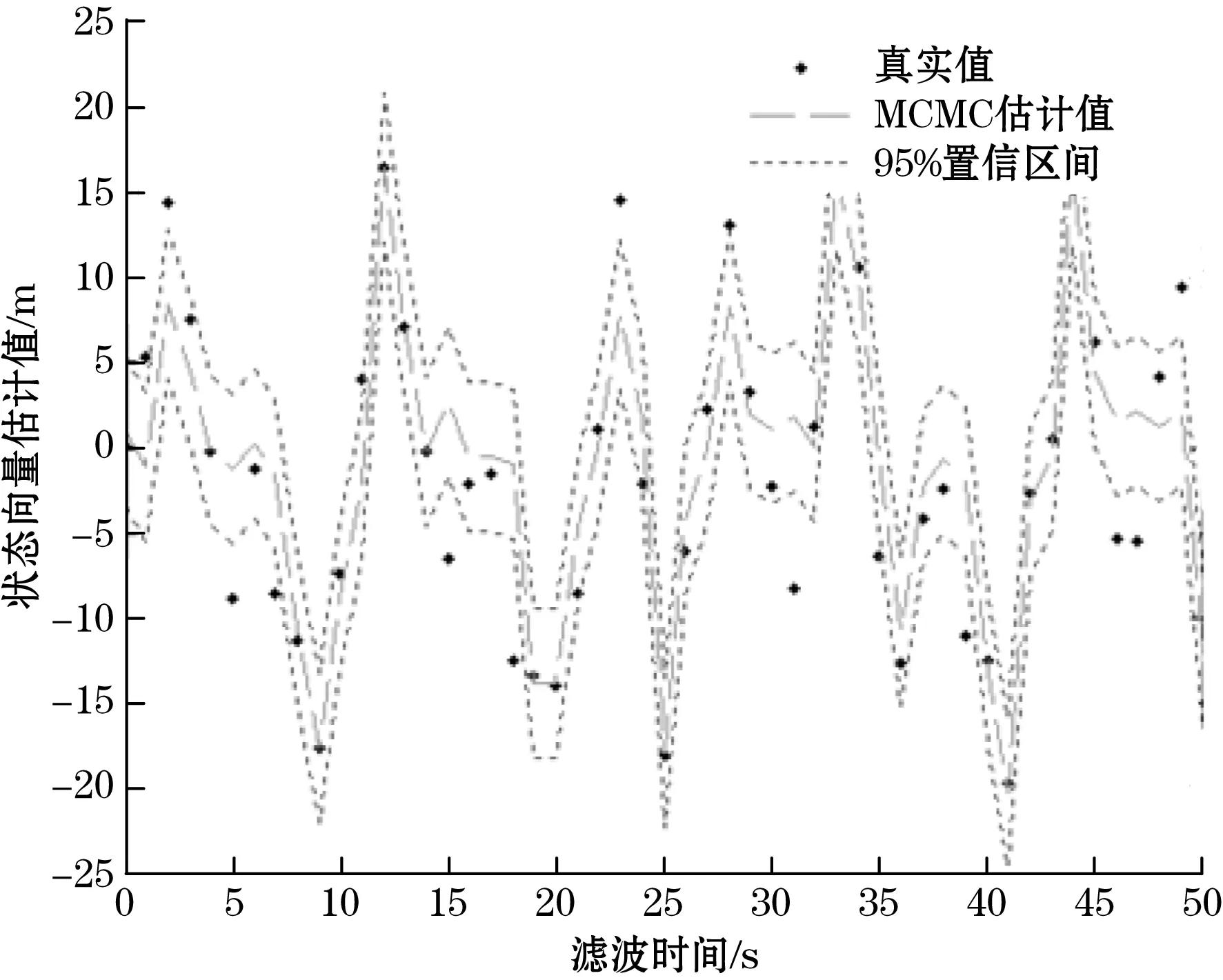
图2 MCMC粒子滤波状态向量估计值

由图3可以看出，由UKF、PF和MCMC粒子滤波算法得到的滤波结果虽然都能逼近真值，但MCMC粒子滤波算法逼近真值的程度会更好一些。

图3 各算法的状态向量估计值与真实值

由图4可以看出，分别采用UKF、PF和MCMC粒子滤波时，通过MCMC粒子滤波算法得到的状态估计值误差始终很小且相对稳定，没有出现类似于UKF和PF的状态估计值误差那样发散的趋势，因此，也可说明MCMC粒子滤波算法优于UKF和PF等算法。

图4 各算法的状态向量估计值误差

仿真得到的各算法估计误差均分值如表1所示。

表1 各算法估计误差均方值

由仿真结果可知，采用的MCMC粒子滤波作为一种非线性的滤波算法，避免了对状态方程的线性化，减少大量线性化误差，并可有效抑制传统粒子滤波(PF)算法的粒子退化问题，增加粒子多样性，提高滤波精度。

4.2 复化Newton-cotes算法实验

4.2.1 实验步骤

为了验证复化Newton-cotes算法在面积计算精度上优于传统求积算法，本文引用张汶贤文中的一个实例区域[27],分别应用梯形法、Simpson 1/3、Simpson 3/8和复化Newton-cotes算法进行面积测算。具体步骤如下：

(1)首先，对于参考面积已知的图例区域以1 m为间隔分别得到区域边界各坐标点，图例区域如图5所示。

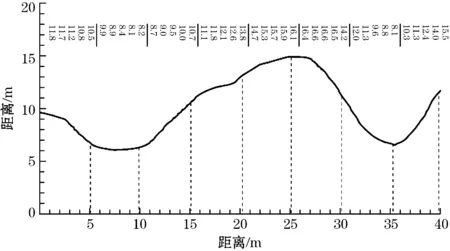
图5 图例区域

(2)对于该图例区域，分别采用梯形法、Simpson 1/3法、Simpson 3/8法以及复化Newton-cotes算法计算其面积，对比各面积结果及相对误差。

4.2.2 实验结果

由上述4种求积算法计算所得的面积值及相对误差如表2所示。其中参考面积为430.78 m2。

表2 计算结果对比

对比以上4种求积算法对同一目标区域面积的计算结果可知，在定位坐标精度一定的条件下，采用复化的Newton-cotes算法的计算误差最小，精度最高。虽然高次插值能增大舍入误差，且容易出现龙格现象，但通过改进方格法和复化的低次Newton-cotes算法相结合，对积分区间进行多次细分，既避免了由高次插值带来的舍入误差，又进一步达到了细分积分区间的目的，大幅提高了面积计算的精度。

5 结束语

综上所述，测量不规则区域面积的新方法在坐标定位方面，采用集DGPS与MCMC粒子滤波于一体的组合定位，由Matlab仿真结果知，在改善滤波效果的同时，其修正定位数据偏差，使得定位精度大幅提高；在面积计算方面，采用复化Newton-cotes算法计算数值积分，由实际测算结果知，其既避免由高次插值带来舍入误差，又达到对面积区间进一步细分的目的，从而大幅提高面积的计算精度。经实验测算，该方法与其他传统方法相比具有精度高、速度快、误差小、抗干扰性强等优越性，可以广泛地应用于林业、农业、城市规划以及水利建设等诸多领域中。同时，本研究将进一步探索基于GPS的不规则自由曲面面积的测量方法[28-29]。

[1] 张全法，韩要轩，杨海彬，等.用面阵CCD测量不规则平面物体的面积. 仪表技术与传感器，2000(2):31-34.

[2] 关胜晓.不规则形体面积的CCD测量研究.仪表技术与传感器，1998(11):36-39.

[3] ANTHONY C, JINLING W, CHRIS R. Bridging GPS outages in the agricultural environment using virtualite measurements. Location and Navigation Symposium, 2008, 7(6):497- 504.

[4] 张海涛，杨敏华.不规则区域面积的矩形四等分割计算法.测绘与空间地理信息，2011，34(6):272-274.

[5] 冯仲科，刘永霞，王小昆，等.林地面积量算方法的比较研究.北京林业大学学报，2004，5(2):97-101.

[6] YONG H, HAIHONG Y, HUI F. Study on improving GPS measurement accuracy. Instrumentation and Measurement Technology Conference, Canada, 2005.

[7] 宋鄂平，张前勇.CASS在林权调查面积量算中的应用.湖北民族学院学报(自然科学版)，2009，27(1):105-108.

[8] MICHIEL D. GPS based bistatic radar - beyond specular reflection. 24th Digital Avionics Systems Conference, Williamsburg, VA, USA, 2005.

[9] GUPTA S, LOW M, TAN C. The new approach of simulate GPS measurements. Position Location and Navigation Symposium, 1998, 7(1):236-242.

[10] 冯仲科，梁长秀，南永天.超小图斑面积的RTD GPS量测.林业资源管理，2001，5(3):70-72.

[11] SHUPING G, ZHANGHAO Z, MATTHEW T. GPS Spoofing Based Time Stamp Attack on Real Time Wide Area Monitoring in Smart Grid . IEEE Smart Grid Comm 2012 Symposium - Cyber Security and Privacy, Nepal, 2012.

[12] ABDEL-SALAM M. Precise point positioning using un-differenced code and carrier phase observations. IEEE International Conference, Canada, 2005.

[13] 田世君，陈俊，皮亦鸣.粒子滤波在高动态GPS定位中的应用.测绘学报，2007，36(3)：274-278.

[14] JULIER S, UHLMANN J. A new extension of the Kalman filter to nonlinear systems. Proceedings of SPIE, 1997, 2(3)：182-193.

[15] JULIER S, UHLMANN J. A new method for the nonlinear transformation of means and covariance in filters and estimators .IEEE Transactions on Automatic Control, 2000 , 45(3):477-482.

[16] 王尔申，蔡明，庞涛.MCMC粒子滤波的GPS定位数据处理算法.数据采集与处理，2013，28(2):213-218.

[17] 秦臻.改进的粒子滤波及其在GPS动态定位中的应用.全球定位系统，2010，5(1):25-28.

[18] 高静，李善姬，邵奎军.MCMC粒子滤波算法研究及应用.电子测试，2009，12(1):19-22.

[19] LIU J, CHEN R .Sequential Monte Carlo methods for dynamic systems. J Amer Statist Assor, 1998, 9 (3):1032-1044.

[20] SANJEEV M, MASKELL S. A tutorial on particle filters for online nonlinear /non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing, 2002, 50(2):174-188.

[21] LIU J, COLAJANNI. Dynamic load balancing on Web-server systems. IEEE Internet Computing, 1999, 3(3):28-39.

[22] IKOMA N, ICHIMURA N, HIGUCHI T, et al. Particle filter based method for maneuvering target tracking. In Proceedings of the IEEE International Workshop of Intelligent Signal Processing, Budapest,2010 .

[23] 赵琳，聂琦，高伟.基于MCMC方法的正则粒子滤波算法及其应用.仪器仪表学报，2008，29(10)：2156-2162.

[24] HU H, JING Z, LI A, et al. An MCMC-based particle filter for tracking target in glint noise environment. Journal of Systems Engineering and Electronics, 2005, 12(2)：305-309.

[25] SPALL J C .Estimation via Markov chain Monte Carlo. IEEE Control Systems Magazine, 2003, 23(2):34-45.

[26] 王金铭，刘艳秋，陈欣.数值分析.大连：大连理工大学出版社，2007.

[27] 张汶贤.计算不规则图形面积的一个新公式.江汉石油学院学报，1989，11(4):83-88.

[28] 胡丹，李敏，常江.复杂轮廓曲面非接触三维数据测量的研究. 仪表技术与传感器，2002(7):23-25.

[29] 王菽芳，邱自学，袁江，等.集成激光位移传感器与线性编码器的自由曲面测量方法及系统. 仪表技术与传感器，2010(7)：4-9.

作者简介：王志超(1990—)，硕士，主要研究领域为高精度不规则图形区域面积测量、中央空调控制器设计等。 E-mail：694428961@qq.com 曹起武(1979—)，副教授，硕士，主要研究领域为智能控制、软件与网络等。E-mail：caoqiwu@163.com

Region Area Measurement Method Based on MCMCParticle Filter and Compound Newton-cotes Algorithm

WANG Zhi-chao1, CAO Qi-wu2, ZHANG Quan1

(1.School of Information Engineering, Shenyang University of Technology, Shenyang 110870, China;2. Department of Information, Liaoning Mechanical and Electrical Polytechnic, Dandong 118009, China)

To improve disadvantages of irregular-area measurement in positioning accuracy and area calculation accuracy, a new area measuring method which has characteristics of high precision and tiny area error was proposed in this paper. It combined the differential GPS measurement system and Markov chain Monte Carol particle filter to locate. And it fitted the boundary curve and calculated areas through the compound Newton-cotes algorithm. The new method used MCMC particle filter to process GPS data. The filter algorithm processed the non-Gaussian distribution noise and improved particle degradation. And the new method used compound Newton-cotes algorithm to calculate the area. The quadrature algorithm avoided the rounding error brought by the high-order interpolation, and further subdivided the area. Therefore, the new method improved positioning accuracy and area calculation accuracy. Experimental results show that the new method has characteristics of high accuracy and tiny errors.

irregular regions; area measurement methods; DGPS; Markov chain Monte Carlo (MCMC); particle filter (PF); compound Newton-cotes algorithm

马俊(1990—)，硕士研究生，主要研究方向为电力电子和嵌入式系统。E-mail:mark41@163.com 李春茂(1963—)，教授，博士学位，主要研究领域为控制系统与电工理论。E-mail:chunmao@126.com

辽宁省科技厅基金项目(20130125)

2014-02-24 收修改稿日期：2015-03-20

P218

A

1002-1841(2015)06-0121-06