基于小波熵自适应最佳分解层数确定算法

崔 治，李加升

(湖南城市学院通信与电子工程学院，湖南益阳 413000)



基于小波熵自适应最佳分解层数确定算法

崔 治，李加升

(湖南城市学院通信与电子工程学院，湖南益阳 413000)

针对超声信号小波阈值去噪中最佳分解层数的选取问题，提出基于小波熵的自适应分解层数确定算法。该算法首先利用离散小波变换分解含噪信号，计算分解后信号子区间的小波熵，然后将细节系数与原始信号的熵之比和低频子带均方根误差相结合以确定最佳分解层数。最后利用信噪比(SNR)、均方根误差(RMSE)、峰值相对误差(REPV)和峰位置误差(EPP)四项指标对算法性能进行评估。仿真和实验的结果表明：该算法能自适应地确定最佳分解层数，在有效滤除含噪超声信号中的噪声、提高性噪比的同时，还能更有效地保留原始信号中的有用成分。

最佳分解层数；小波熵；超声信号；自适应

0 引言

超声波在传输过程中会受到仪器电噪声、材料晶粒散射噪声等的影响，使得接收到的陷信号往往淹没在噪声中，易造成误判或漏判[1]。对超声信号进行小波阈值去噪是一种行之有效的去噪方法，大量的实验表明，在选择小波基和设计阈值函数之外，小波分解的层数也是影响超声信号阈值去噪结果的重要原因。研究者们在定量确定分解层数方面的成果主要集中在以下两方面：

(1)基于噪声检验，根据信号与噪声小波分解的不同传播特性来确定最佳的分解层数[2-3]；

(2)基于奇异值分析，根据对信号进行分解后各层小波系数的奇异值斜率来决定最佳分解层数[4-5]。

但是，基于噪声检验的方法需要获取噪声特征序列这一先验条件，在超声检测的实际环境中往往难以满足；基于奇异值分析的方法需要根据信号各层小波分解系数的奇异值特性，计算相应的奇异值斜率并通过与一个阈值斜率进行比较来确定最佳层数，计算量大，也难以设置合适的阈值斜率。鉴于此，本文融合小波分解细节系数熵之比和低频带均方根误差两项指标，提出一种基于小波熵的自适应最佳层数确定算法，以仿真的超声信号和实地采集的缺陷波为例，利用信噪比(SNR)、均方根误差(RMSE)、峰值相对误差(REPV)和峰位置误差(EPP)对算法的性能进行评估。

1 超声信号的去噪原理

在超声检测过程中，电源电压的波动、静电干扰、接地不良等仪器因素和超声波在被检测试样内部传播时遇到异质界面和粗晶粒所造成的散射与反射都会对超声信号造成影响，这些噪声一般都表现为平坦的宽带特性，因此在研究时可以看作是加性高斯白噪声。这样，一个包含有噪声的原始超声信号f(k)可以用下面的公式来表示：

f(k)=r(k)+e(k)(i=1,2,…,N)

(1)

式中：r(k)为真实超声信号；e(k)为噪声。

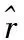
(2)

对原始信号f(k)进行离散小波变换后，损失函数转化为

(3)

由上述分析可知，在小波域内对含噪超声信号进行去噪的问题就转化成了使式(3)所表示的损失函数获得最小解的问题。在小波域内，信号的能量往往集中体现在小部分幅度比较大的小波系数上，而噪声由于其频率和能量谱相对分散，因此噪声的小波系数绝对值比较小，且能量分散在大部分的小波系数上。因此，在对含噪信号进行小波分解的过程中，当分解到最佳层数后，有用信号的小波系数将大于噪声的小波系数，这样，通过阈值收缩方式即可实现对含噪信号的去噪处理。

2 本文算法设计

2.1 小波分解细节系数熵之比

在信息论中，熵用来表示信源中所有符号包含信息量和不确定度的均值，它代表了信号在动态过程的有用信息。对信号进行多尺度小波变换，将所得的各尺度小波系数转换成概率分布序列，由这个序列计算得到的熵值的大小反映了小波系数矩阵的稀疏程度，或者说，反映了信号的不确定度和复杂度。

设信号f(t)经离散小波变换后，在第j分解尺度下k时刻的细节系数为dj,k，近似系数为aj,k，则尺度为j时(j=0,1,…，M)的细节能量为

(4)

式中Cj(k)为对应的小波系数，Cj(k)=[f(t),Ψj,k(t)]。

信号总能量为

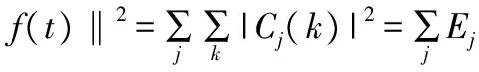
(5)

相对小波能量可以表示为Pj=Ej/E。将第j层分解的细节系数Cj(k)均分为n个子区间，有

(6)

式中m为采样点数。

每个子区间的相对小波能量Pj,i可由对应的第i个子区间的小波能量Ej,i与该层小波系数总能量相比求得：

Pj,i=Ej,i/Ej

(7)

(8)

可得第i个子区间对应的小波熵Wi为

(9)

分别计算原始信号的熵W0和第j层分解细节系数的小波熵Wj，则熵之比η为

η=Wj/W0

(10)

小波分解的层数越多，得到的细节系数的熵越小，表明信息的确定性越大。文献[7]认为，当某层分解细节系数小波熵与原始信号的熵之比为5%时，可视作细节系数已确定。

2.2 均方根误差

设原始信号为f(k)，第j层分解的低频带为fj(k)，则均方根误差为

(11)

式中N为信号的长度。

2.3 算法设计

根据上述指标，提出确定小波分解最佳层数的算法如下：

(1)计算出小波分解细节系数熵之比大于5%的最大分解层数m和熵之比小于5%的最小分解层数n，m和n满足:

m=n-1

(12)

(2)计算对应分解层数的均方根误差Em和En；

(3)确定最佳分解层数j:

(13)

3 评价指标

为了验证本文提出的小波分解最佳层数选取方法，采用信噪比(SNR)、均方根误差(RMSE)、峰值相对误差(REPV)和峰位置误差(EPP)四项指标对超声信号的去噪效果进行评估。其中，峰值相对误差(REPV)和峰位置误差(EPP)定义如下：

(14)

式中：Ti为原始信号的峰值；To为经去噪处理后信号的峰值。

EPP=Si-So

(15)

式中:Si为原始信号的峰位置；So为去噪处理后信号的峰位置。

峰值相对误差反映了去噪后信号能量损失的程度，在超声检测中，缺陷波的幅值与形状将影响对缺陷种类和大小的判断；峰位置误差反映了信号去噪后出现时间失真的程度高低，在超声检测中，缺陷波的出现时间与缺陷位置直接相关。由此可见，信噪比越高，均方根误差、峰值相对误差和峰位置误差越小，表明信号去噪的效果越好，原始信号中的有用成分被保留得越完整。

4 仿真分析

超声检测中的缺陷回波是一种被探头中心频率调制的非平稳信号，根据经验，一般可以用下式来模拟[8]：

h(t)=ρe-μ(t-τ)cos[2πf(t-τ)]

(16)

为了验证本文算法的性能，首先在MATLAB7.0环境下进行效果分析。图1(a)是式(16)所示的仿真信号，各参数取值为ρ=3.24，μ=1012，τ=5×10-6，f=2×106。图1(b)是加入σ为15的白噪声后的信号。可以看到，由于噪声的影响，回波幅值已发生明显改变，有用信号被淹没在了噪声中。对信号进行去噪时还存在选择最佳小波基的问题，本文选择Sym-4小波、软阈值函数对原始信号进行阈值去噪[9]。首先采用本文提出的方法来判定最佳分解层数。经计算，当分解层数为5时，熵之比为0.051 7，均方根误差E为6.153；分解层数为6时，熵之比为0.049 1，均方根误差E为5.947，据此可以确定最佳分解层数为6。

(a)原始仿真信号

(b)加噪信号图1 仿真信号及加噪信号

与此同时，在MATLAB中对该原始信号分别进行2～9层分解并计算各项指标，得到评价结果如表1所示。从表1可以看到，分解层数为6时，均方根误差(RMSE)和峰值相对误差均为最小，增大分解层数到9层后信噪比有所提高，但增幅非常小(约为0.104%)，而均方根误差(RMSE)和峰位置误差则分别增大了1.874%和38.71%，峰值相对误差更是从0.62%增至5.20%，增幅达到8倍。后三项指标的增大表明此时信号出现失真，将导致误检或漏检，同时运算量也会大大增加。因此，综合各种评价指标后，最佳分解层数应该是6，这与采用本文算法进行计算的结果一致，表明了本文算法的可行性。

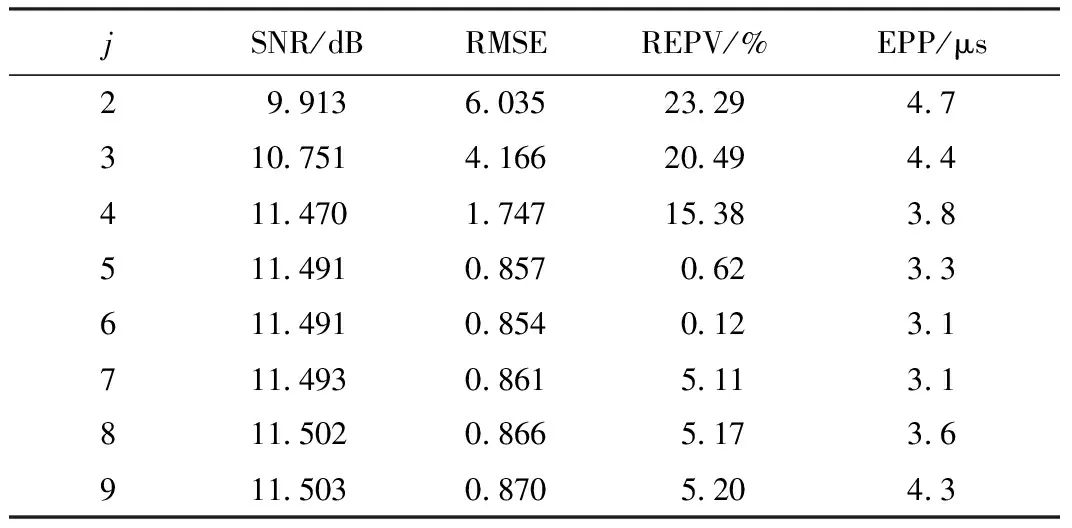
表1 不同分解层数下的评价指标

分解层数为2、6和9的信号如图2所示。从视觉主观来看，图2(b)的效果已经达到了最佳，6层分解是最佳层数。

为了进一步判断本文算法的可靠性，对式(16)的仿真信号添加σ为5、20、25、30、35的白噪声，分别采用本文算法计算最佳分解层数，通过比较2～9层分解下不同的评价指标来进行验证，得到结果如表2所示。

(a)2层分解

(b)6层分解

(c)9层分解图2 分解层数为2、6、9时的结果

由表2可知，当待处理信号的信噪比较高时，采用较少的分解层数就能获得比较理想的结果，当待处理信号的信噪比较低时，分解层数必须有所增加。本文算法能根据信号中噪声水平的不同而自适应的选择最佳分解层数，避免了过高分解层数造成的信号失真，有助于提高超声检测的效率，也避免了计算资源的浪费。在噪声水平难以事先确定的超声检测中，本文算法是有效的。

表2 不同噪声水平下的最佳分解层数

5 实验及结果

实验中所用的试件为整体厚度为1 cm的γ-TiAl合金层压板，允许形变±0.5%，在制备过程中预先置入缺陷，探头选择中心频率为5 MHz的5L64-A2型直探头，用单侧自发自收A扫描方式采集到一个含噪信号，通过时闸门将缺陷回波截取出来，在MATLAB中如图3(a)所示。对该信号进行小波阈值降噪，小波基为Sym-4。分解层数为2～9时对应的评价结果如表3所示。由表3可见，分解层数为6时，峰值相对误差和均方根误差(RMSE)均为最小，说明此时信号去噪的效果最好，原始信号中的有用信息被最大可能地保留了下来，分解层数大于6后信噪比有微量增加，同时均方根误差(RMSE)、峰值相对误差和峰位置误差开始增大。综合起来最佳分解层数应为6。采用本文提出的方法进行计算，当分解层数为6时，熵之比为0.054 1，均方根误差为5.343，分解层数为7时，熵之比为0.044 7，均方根误差为7.101，据此确定最佳分解层数为6，与实际结果一致。

表3 不同分解层数下的结果对比

分解层数为2、6和9的信号如图3(b)-图3(d)所示。由图可见，2层分解对噪声的滤除不够彻底，9层分解后信号非常光滑，但与6层分解的结果相比，信噪比仅提高了0.284%，均方根误差和峰位置误差却增大了0.649%和24%，峰值相对误差增大了1.46倍，表明此时信号已出现较大的失真，会导致错误的检测结果。分解到6层是最佳层数。

6 结论

本文提出了一种基于小波分解细节系数熵之比和低频带均方根误差两个标准的最佳小波分解层数确定方法，仿真和实验表明，该方法在有效提高信噪比的同时，还能有效降低均方根误差、峰值相对误差和峰位置误差，从而更加完整地保留原始信号的特征。构造新的阈值函数和设计自适应阈值规则将是下一步的研究方向。

[1] 李文强, 杨录. 超声回波门参数数字化控制方法的研究与实现. 仪表技术与传感器, 2012(7)：100-104.

[2] 迟大钊, 刚铁, 姚英学. 基于非线性小波收缩的超声信号缺陷识别方法. 机械工程学报, 2011, 47(18)：1-6.

[3] 蒋科荣, 唐向清, 朱德泉. 基于改进阈值的汽车轮速信号处理. 仪器仪表学报, 2010, 31(4)：736-740.

[4] 高国荣, 刘艳萍, 潘琼. 基于小波域可导阈值函数与自适应阈值的脉冲星信号消噪. 物理学报, 2012, 61(3)：1-5.

[5] 汪琴, 陈雨, 谭斌, 等. 基于提升小波的压电埋入式超声信号的改进阈值降噪. 应用力学学报, 2013, 30(4)：539-543.

[6] 陈思凤, 刘业政. 混合状态变量和过程变量的风险评估模型. 控制与决策, 2013, 28(2)：309-312.

[7] 陈玉明, 吴克寿, 李向军. 一种基于信息熵的异常数据挖掘算法. 控制与决策, 2013, 28(6)：867-872.

[8] BETTAYEB F，RACHEDI T，BENBATAOUI H. An improved automated ultrasonic NDE system by wavelet and neuron networks. Ultrasonics, 2004, 42：853-85.

[9] 崔治, 崔宪普, 肖卫初.γ-TiAl超声检测中基于多分辨率分析的小波选取. 铸造技术, 2012, 34(3)：304-307.

Determination Algorithm of Optimal Decomposition Level via Wavelet Entropy

CUI Zhi, LI Jia-sheng

(School of Communication and Electronic Engineering, Hunan City University, Yiyang 413000, China)

Aiming at the problem of how to select the optimal level of wavelet for ultrasonic signal denoising, an improved wavelet entyopy based method by combining the entropy ratio and the root-square-mean error of low bands was proposed. When the discrete wavelet transform was applied in the signal decomposition, the wavelet entropy at decomposed levels was calculated, then the entropy ratio and the root-square-mean error of low bands were used as the deciding threshold to choose the optimal decomposition level. The signal-to-noise ratio, the root-square-mean error, the relative error of peak value and the error of the peak position were used to evaluate the performance of the method. Simulation and experimental results show that the proposed method can adaptively determine the optimal decomposition level, remove the ultrasonic signal noise and keep the useful information effectively.

optimal decomposition level; wavelet entropy; ultrasonic signal; adaptive

(a)实地采集的信号

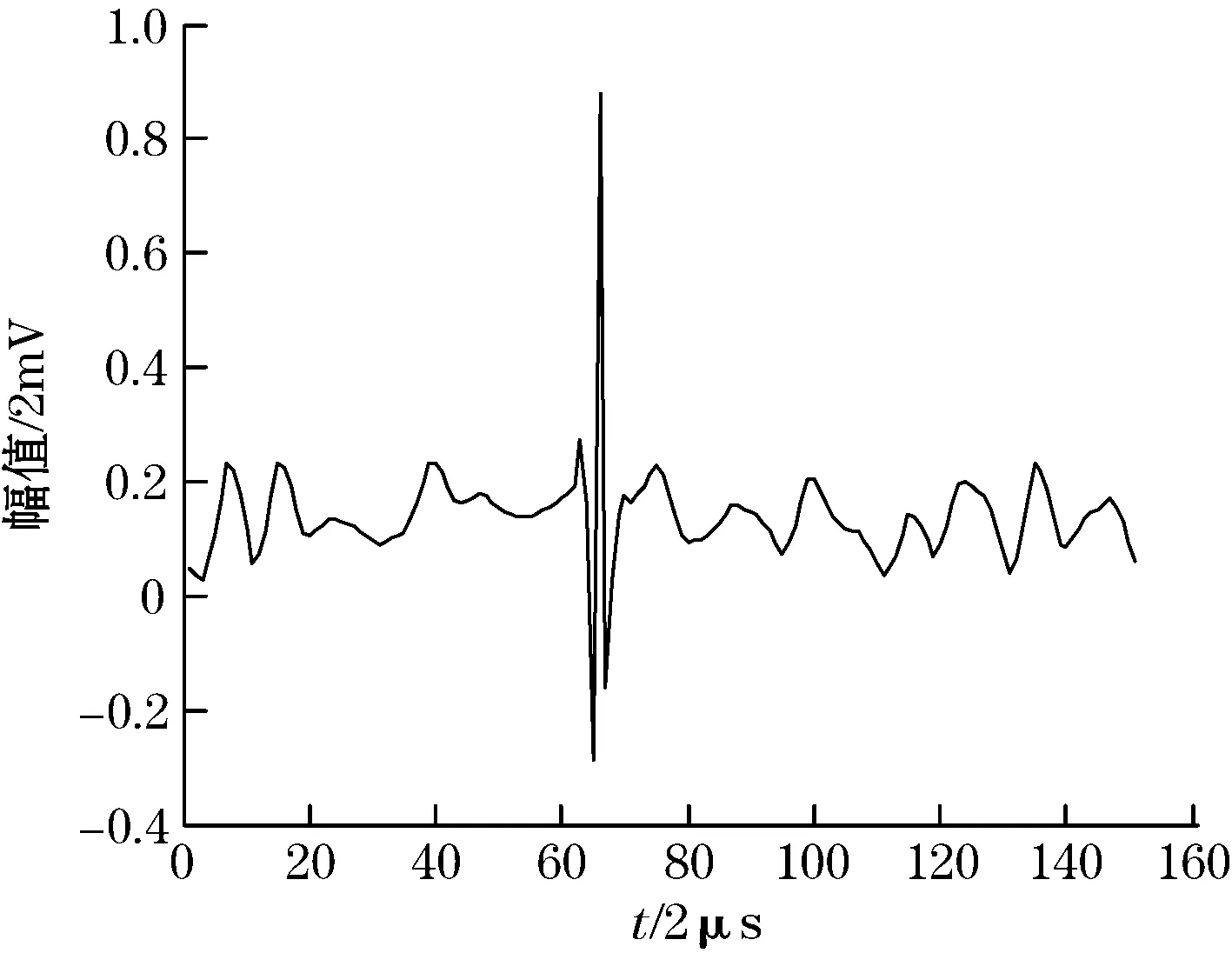
(b)2层分解

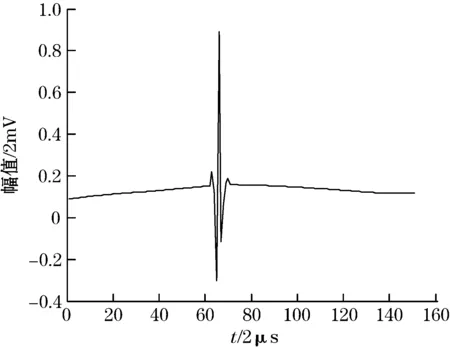
(c)6层分解

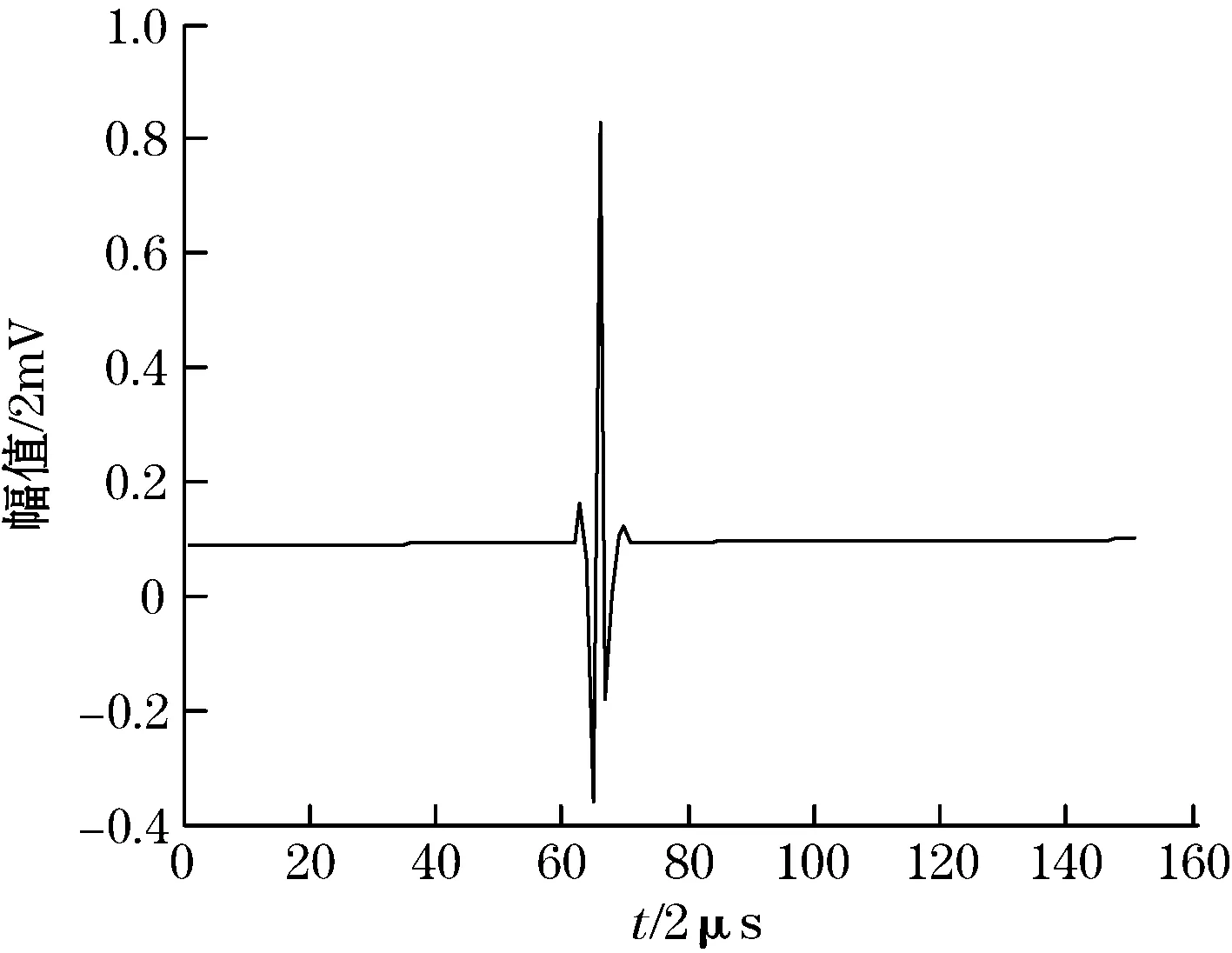
(d)9层分解图3 实地采集的信号及其2、6、9层分解的结果

湖南省教育厅科研项目资助(13C122)；湖南省自然科学基金资助项目(13JJ6072)

2014-07-30 收修改稿日期：2015-03-27

TP216.1

A

1002-1841(2015)06-0127-04