时序与主成分分析的钢框架模型损伤识别研究

王嘉琛,逯静洲,高 倩,朱 旭

(烟台大学土木工程学院,山东 烟台 264005)

时序与主成分分析的钢框架模型损伤识别研究

王嘉琛,逯静洲,高 倩,朱 旭

(烟台大学土木工程学院,山东 烟台 264005)

针对结构健康监测中基于时间序列分析实现损伤识别的问题,提出了一种利用AR模型的均方差根误差(RMSE)与主成分分析(PCA)的结构损伤识别方法.首先对加速度数据建立自回归AR模型,并求得模型的均方根误差.然后,采用主成分分析获取载荷矩阵,通过标准化处理后提出结构损伤特征指标并定位损伤发生的位置.为验证本文提出方法的可行性,对不同损伤工况下的钢框架模型进行了振动试验,利用该方法对各种损伤状况进行识别,识别结果与预设损伤情况相一致.结果表明,使用该方法可以充分利用大量实测数据,克服外界干扰因素所带来的影响,对于结构的损伤诊断具有较高的理论价值和实用价值.

损伤识别;钢框架结构;时间序列;主成分分析;自回归(AR)模型

基于结构振动特性的损伤识别方法作为结构健康监测领域研究的前沿方向,在建设和服役期间保障了结构的安全状况,在国内外受到了广泛的关注.结构健康监测技术在统计模式识别框架下分为4步[1]:一是进行数据采集和预处理(标准化处理);二是进行系统动态建模;三是对结构的损伤特征进行提取;四是对结构的状态特征进行分类识别.通过振动测试获取动力响应数据,利用时间序列分析方法建立差分形式的模型,再利用模型所识别的损伤参数来进行特征提取和统计判别.为使模型更好地反映真实情况,得到更为科学、准确的信息,采用主成分分析把原始高维相关的变量处理转换成少量相互独立的向量.美国Los Alamos国家实验室[2-3]对基于时间序列分析的损伤识别方法进行了大量研究,利用加速度响应数据样本建立自回归AR(Auto-Regressive)模型,将AR模型系数定义为损伤识别敏感性指标,分别在结构完好和损伤状态下计算AR模型系数之间的马氏距离,从而实现损伤定位.Doebling S W, Sohn H, Farrar C R等[4-5]详细介绍了近年来在结构健康监测领域内,基于振动测试的结构损伤识别方法的发展状况.刘毅等[6]采用高斯白噪声作为基底激励源,以获取结构模型加速度响应数据建立ARMA模型,提出了结构损伤预警的实现方法,并以三跨连续梁数值算例证明了方法的有效性.马高等[7]利用时间序列模型和系统的联系,采用结构振动响应的仿真数据建立了自回归滑动平均模型,取ARMA模型AR部分前三阶系数的代数组合作为损伤敏感因子,利用ASCE损伤检测标准模型进行了相应的损伤识别的数字仿真实验,证明了时间序列方法的可行性.

理论研究表明:主成分分析法对原始数据压缩降维的同时,又可有效的保留原始数据的特征信息,排除外界干扰因素,减少运算量,可对损伤源进行定位,具有较高的损伤识别精度[8].

本文对完好和不同损伤程度的钢框架模型分别进行了振动试验分析,验证了基于AR模型均方根误差及主成分分析方法的有效性.以高斯白噪声作为激励源,获取加速度响应数据作为损伤识别的原始数据,建立各组数据的AR模型,求得模型的均方根误差,对模型均方根误差进行主成分分析获得载荷矩阵,将此矩阵经过数据标准化处理得到结构损伤特征指标,根据该指标对结构损伤状态进行识别和定位.

1 基于时序与主成分分析的损伤识别方法

1.1 自回归模型建立

平稳、正态、零均值的时序是建立AR模型的前提条件.已知时间序列{Xt},t=0,1,…,k,标准化处理后得[9-10]

(1)

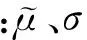
时间序列{Xt},其中t=0,1,…,k,白噪声序列表示为{λt},λt～NID(0,σ2),回归系数Ψα,其中α=1,2,…,p,可得到AR模型:

(2)

本文采用AIC信息准则法定阶[11];采用最小二乘法进行参数估计;采用自相关函数法对模型的独立性作出判断.

若结构损伤存在,则实测值与预测值之间必然存在较大误差,采用均方根误差(RMSE)来衡量两者之间的偏差.

均方根误差计算公式为

(3)

1.2 主成分分析

主成分分析最重要的应用是采取数学降维的思想对原有数据进行简化,用较少的几个综合变量指标代替原来较多的变量指标,准确地反映原始变量的信息[12-13].

在数学上的处理方法是将原始变量做线性组合,适当调整组合系数,成为新的相互独立并且具有代表性的变量指标.数据经过标准化处理后,求得相关系数并构成矩阵,根据样本协方差估计值求得矩阵的特征值与特征向量,用累积贡献率来确定主成分个数,得到相应的载荷矩阵V.载荷矩阵可以体现结构在同一拾振点处不同激振工况下的不同响应状况.

1.3 损伤特征指标

1.3.1 综合权重矩阵B综合权重矩阵B体现了结构的原始响应状况与经数据压缩变换后结构响应状况的差异.首先对主成分分析后得到的载荷矩阵V进行归一化处理,然后,求得结构整体权重矩阵,即将荷载矩阵V与其转置相乘,最后将单位矩阵E与上述结构整体权重矩阵作差,得到综合权重矩阵.

综合权重矩阵B:

B=E-V×V' .

(4)

1.3.2 判定指标D将AR模型均方根误差矩阵R与综合权重矩阵B相乘,得到结构在相同激振条件下不同拾振点处响应状况的差别,即

R×B=R×(E-V×V′) .

(5)

判定指标值Di即为

(6)

其中:i表示传感器数目,i=1, 2,…,m,j表示试验次数j=1, 2,…,n.计算其算术平方根可消除原数据正负数值的影响.

损伤判定指标Di可以对损伤进行识别与定位,但损伤识别与定位的程度不够明显,为进一步突出结构损伤状态与无损状态下的区别,需增强该判定指标的敏感性.

1.3.3 损伤特征指标DI 定义完好工况为基准状态,将结构所有工况下的指标Di与基准状态下的指标D基准作比值,得到指标值D'i,即

(7)

式中:i表示传感器数目,i=1, 2,…,m.

各工况状态下的指标值与结构完好状态下指标值作差,得到的差值即为损伤特征指标DI,若损伤特征指标值DI大于零判定结构为损伤状态.

基于时序与主成分分析的结构损伤识别流程如图1.

2 钢框架模型损伤识别试验

2.1 试验概况

本试验采用剪切型钢框架作为研究对象,利用HEV-50型激振器进行激励,系统产生的结构振动响应由INV9822型ICP接触式传感器拾振得到.

试验模型是3层剪切型钢框架,框架总高为1 000 mm,楼板间的净高为330 mm.楼板为Q235的钢板,尺寸为300 mm×200 mm×15 mm;立柱为Q235的弹簧钢,尺寸为30 mm×3 mm.楼板与立柱连接处的节点采用2个螺栓与夹紧板实现刚性连接,螺栓为Q235的钢材,直径为10 mm.框架结构底部由钢板和螺栓固定在振动台上.

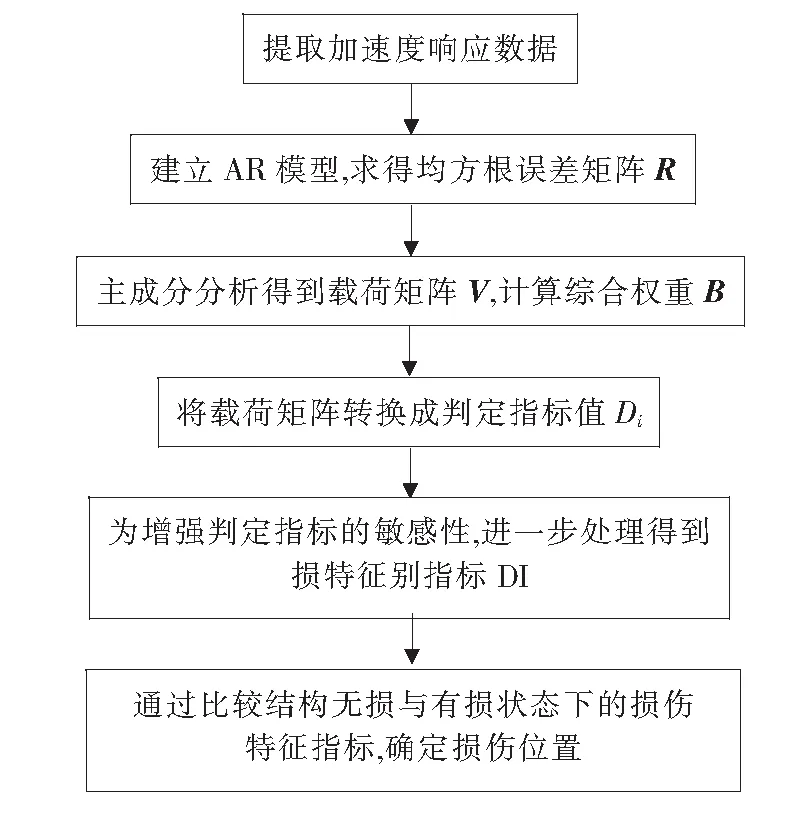
图1 基于时序与主成分分析损伤识别流程

Fig.1 The procedure of structural damage detection based on the time series and principal component analysis

本试验测点设置在结构第一层板侧向中心部位,电磁激振器沿着结构的中心线对框架模型提供了侧向激励.在与刺激源相对的每层钢板中点设置加速度传感器.共测量4个通道的信号,自下而上为通道一、通道二、通道三、通道四,通道五收集激励力的大小,位置在第二层板处并与通道二的传感器相对.采用白噪声激励,激励部位和传感器布置如图2.

图2 钢框架模型

采样频率为25.6 Hz,在激振器开始激振10 s后开始采样,采样时间为30 s,每组工况取前1 000个数据,以每组100个数据把响应数据分成10组.

2.2 结构损伤的模拟

楼板与立柱通过螺栓与夹紧板连接,本试验的损伤模拟是通过减少节点处的螺栓来实现,损伤状况如表1,以第一组工况为基准状态.

表1 钢框架模型振动试验的损伤工况设置

Tab.1 Damage condition settings of steel frame model vibration test

工况状态状态设置工况1工况2工况3工况4工况5工况6工况7完好(0%)小损伤(50%)损伤(100%)小损伤(50%)损伤(100%)小损伤(50%)损伤(100%)基准状态去掉一个螺栓去掉2个螺栓与夹紧板去掉一个螺栓去掉2个螺栓与夹紧板去掉一个螺栓去掉2个螺栓与夹紧板

3 钢框架损伤识别试验结果分析

测量结构加速度响应数据,根据偏自相关函数法确定AR模型阶数为15,根据公式(3)计算出AR模型的均方根误差矩阵,主成分分析后经过标准化处理得到损伤特征指标值DI,试验结果如图3.

根据AR模型参数均方根误差与主成分分析的损伤识别方法,当损伤指标为正值即为损伤,由图3分析可知,通道一的损伤指标均为负值,则该通道无损伤情况发生;通道二在工况2、工况3的损伤指标为正值,则工况2与工况3在通道二附近有损伤发生;通道三在工况4、工况5的损伤指标为正值,则工况4与工况5在通道三附近有损伤发生;通道四在工况6、工况7的损伤指标为正值,则工况6与工况7在通道四附近有损伤发生,分析结果与试验设置相符．说明基于AR模型参数的均方根误差与主成分分析的损伤识别方法对于损伤定位具有良好的应用．

观察图3(b)可知通道二在工况2与工况3的识别指标DI的大小呈递增趋势,观察图3(c)可知通道三在工况4与工况5的识别指标DI的大小呈递增趋势,观察图3(d)可知通道四在工况6与工况7的识别指标DI的大小呈递增趋势,根据试验工况设置,工况2的损伤程度比工况3的降低了50%,工况4的损伤程度比工况5的降低了50%,工况6的损伤程度比工况7的降低了50%,由分析结果可知采用该判定指标对结构的损伤程度也能实现一定的判断．

由试验结果可知,基于AR模型均方根误差法与主成分分析相结合的损伤识别方法对结构损伤具有较高的识别度,可以实现结构的损伤定位与损伤程度的判别,并且对结构小损伤同样具有较高的识别敏感性.

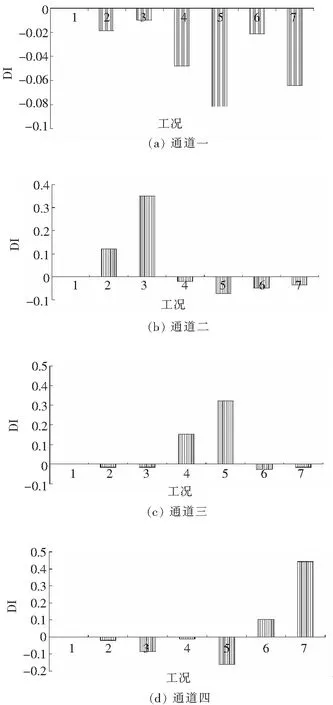
图3 通道一～四各工况损伤特征指标值DI

4 结 论

本文研究了基于时间序列与主成分分析的损伤识别方法,用3层钢框架模型的振动试验验证了本文所提出研究方法的可行性和准确性.

(1) 分析结果表明基于时间序列与主成分分析的损伤识别方法对结构状态的变化具有敏感性,能较准确的识别结构的损伤位置,对结构的损伤程度具有一定的判别能力,对于小损伤识别效果同样显著.

(2) 基于主成分分析的时间序列方法对结构的健康与损伤状态具有稳定的辨识能力,可直接利用加速度响应数据,提取数据中有效的损伤信息.可以用来对结构损伤进行定位与定量分析,便于形成实时监测系统.

[1] Sohn H, Farrar C R. Damage diagnosis using time series analysis of vibration signals[J]. Smart Materials and Structures, 2001,10(3):446-451.

[2] Figueiredo E, Park G, Figueiras J,et al. Structural health monitoring algorithm comparisons using standard data sets[R]. Los Alamos, New Mexico:Los Alamos National Laboratory, 2009.

[3] 朱军华,余岭.基于时间序列分析与高阶统计的结构损伤检测[J].东南大学学报:自然科学版,2012,42(1):137-142.

[4] Doebling S W, Farrar C R, and Prime M B. A summary review of vibration-based damage identification methods[J]. The Shock and Vibration Digest, 1998, 30(2): 91-105.

[5] Sohn H, Farrar C R, Hemez F M, et al. A review of structural health monitoring literature 1996-2001 [R]. LA-13976-MS, New Mexico: Los Alamos national laboratory report, 2003.

[6] 刘毅, 李爱群, 丁幼亮, 等. 基于时间序列分析的结构损伤特征提取与预警方法[J].应用力学学报, 2008, 25(2): 253-256.

[7] 马高, 屈文忠, 陈明祥, 等. 基于时间序列的结构损伤在线诊断[J]. 武汉大学学报, 2010, 40(4): 81-85.

[8] 朱旭, 逯静洲, 徐娜, 等. 基于时间序列和主成分分析的结构损伤识别[J]. 烟台大学学报:自然科学与工程版. 2013, 26(3): 207-211.

[9] 王振龙,胡永宏. 应用时间序列分析[M]. 北京:科学出版社, 2007.

[10] 杨叔子,吴雅.时间序列分析的工程应用(上)[M].武汉:华中科技大学出版社,2007:51-52.

[11] Nair K K,Kiremidjian A S,Law K H.Time series-based damage detection and localization algorithm with application to the ASCE benchmark structures[J]. Journal of Sound and Vibration, 2006, 291(1/2): 349-368.

[12] Housner G W, Bergman L A, et a1.Structural c-ontrol: past, present and future[J].Journal Engineering Mechanics, 1997, 123(9): 897-971.

[13] Farrar C R, Duffery T A, Doebling S W, et a1. A statistical pattern recognition paradigm for vibration-based structural health monitoring[C]//The 2nd International Workshop on Structural Health Monitoring.Stanford: CA,1999.

(责任编辑 苏晓东)

Damage Identification of Steel Frame Based on Time Series and Principal Component Analysis

WANG Jia-chen, LU Jing-zhou, GAO Qian, ZHU Xu

(School of Civil Engineering, Yantai University,Yantai 264005,China)

Aiming at the problem of the time series analysis in structural health monitoring (SHM), a structural damage identification method based on the principal component analysis method (PCA) for the root mean square error (RMSE) of auto regressive (AR) model is presented. Firstly, the AR model is established using acceleration response data, and the root mean square error of AR model is calculated. Then, the load matrix is obtained based on principal component analysis, and the structural damage characteristic index is proposed through standardized processing, on which the accurate location of the damage source is located. To further validate the feasibility of the proposed method, vibration test is conducted in different damage states, and the damage states are detected with the proposed method. The damage identification result is consistent with the predefined damage.Experimental result shows that the suggested method can make full use of a large number of measured data, eliminate the influence of external interference, and has highly theoretical and practical value on damage detection.

damage identification; steel frame structure; time series; principal component analysis; auto regressive(AR) model

1004-8820(2015)04-0289-05

10.13951/j.cnki.37-1213/n.2015.04.010

2015-01-04

国家自然科学基金资助项目(51479174);山东省自然科学基金资助项目(ZR2012EEM014).

王嘉琛(1989- ),女,山东烟台人,硕士研究生.

逯静洲(lujingzhou@sina.com),教授,博士,研究方向:结构的损伤识别.

TU317,O327

A