环路的平均固定时间研究
张培爱
(暨南大学数学系,广东 广州 510632)
环路的平均固定时间研究
张培爱
(暨南大学数学系,广东 广州 510632)
进化图可以动态刻画一个种群的动态演化,定置概率描述进入种群的新突变体占据整个种群的概率,而平均固定时间反映了该种群的平均进化速度.本文研究了环路的平均固定时间.在种群个体数量很大的情况下,给出了环路上单个突变体的平均固定时间及其性质.当相对适应度0
环路;平均固定时间;进化图;固定概率
进化图由Lieberman、Hauert和Nowak[1]于2005年在《Nature》上提出.用一个有向图来刻画一个种群的动态进化[1-9].有向图中的顶点表示种群中的个体,个体间的相互作用由连接顶点的边来表示.在每个时间步,按照一定的规则,随机挑选一个个体进行繁殖,每个个体被挑到的概率与其相对适合度、出度、入度、位置、图的空间结构等有关.被选出的个体取代相邻个体的概率与连接它们的边的权重成正比.当一个突变体(新的个体)在这个种群中出现,这个突变体可能占据整个种群或者从这个种群消失.这个具有一定相对适应度的突变体占据整个种群的概率为定置概率,与种群的个体数量、空间结构、突变体的相对适应度等有关.突变体的相对适合度就是突变体的适应度与种群中原有个体的适应度比值.一个突变体在一个进化图中的定置概率越高,表明这个种群的更新能力更强,系统稳定性就越差[5-8].固定时间被定义为突变个体最终占领整个种群所花费的时间;平均固定时间反映了该类种群的平均进化速度.平均固定时间越少,种群平均进化速度越快.Whigham和Dick[10], Broom等[3],Paley等[11]研究了k-星型图和漏斗图的平均固定时间,并给出了随着相对适应度的增加、平均固定时间也相应减少的结论.Antal等[12]给出了一种在充分混合的种群中的平均固定时间的计算方法.Nie和Zhang[6]得到了在充分大的种群下,等温图和k-星型图的平均固定时间的简单表达公式等.环路是一类特殊的进化图,对于环路中的每个顶点来讲,入度等于出度.权重矩阵W=(wij)不再要求是随机的,权重系数wij可以是任意的非负数.在每个时间步,挑选一条边.挑选概率正比于wij与该边首端个体(即顶点i)的相对适合度的乘积.如果边ij被选择,则i的子代将取代j.由于在许多不同背景下产生的图都是环路,因此,环路的研究具有非常重要的意义.张京友等[13]给出了环路的定置概率,下面我们给出环路中单个突变体的平均固定时间.
1 主要结论
环路作为一种特殊的进化图,张京友等[13]研究了其定置概率,并给出了定置概率随着相对适应度的增加而增加的结论,并应用于知识型企业组织结构.下面我们将计算环路的平均固定时间,得到以下结论.
定理(环路平均固定时间定理) 在一个有N个适应度为1的正常个体、具有环路结构的种群中,如果引入一个相对适应度为r的突变个体,则该突变个体占领整个种群的平均固定时间为
(1)
证明 记环路中的一个个体p,即有向图中的一个顶点p,wi(p)和wo(p)分别表示顶点p的入度和出度.因为进化图G为一个环路,所以每个顶点的入度等于出度,即wo(p)=wi(p)[13].记状态i表示种群中有i个相对适应度为r的突变体和N-i个适应度为1的正常个体情形.状态0表示突变体在该种群中消失,状态N表示突变体占据了整个种群,因此我们称状态0和状态N为吸收状态.
γi=p(i→i)=1-p(i→i-1)-p(i→i+1);
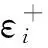
i=1,2,…,N-1.
以上方程可化为如下方程:
(2)


由一维随机游走过程[14-15]可知
pi(t)=μipi-1(t-1)+λipi+1(t-1)+(1-μi-λi)pi(t),
i=1,2,…,N-1,
即
i=1,2,…,N-1.
从而,
由上式可得
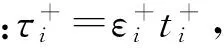
该式可化为
i=1,2,…,N-1.
经过多次迭代得到
其中:qk=r-k.令i=1,2,…,N-1,则

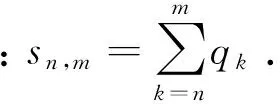

定理证毕.
在上述定理中,我们给出了进入环路中的单个突变体最后占领种群的平均固定时间,下面给出环路的平均固定时间的一个性质.

证明 当r∈(0,1),N非常大时,

可直接计算得
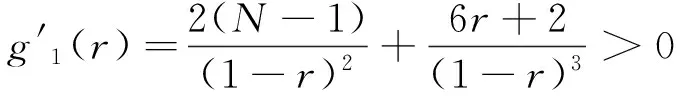

下面讨论当r>1时的情况.
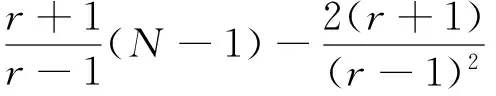
直接结算可得
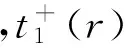
2 结 论
本文给出了环路上单突变体的平均固定时间,并讨论了当种群个体数目非常大,突变个体的相对适应度小于种群中原有个体的适应度,即该突变体是一个劣势突变体时,环路的平均固定时间随着相对适应度的增加而增加,由文献[9]可知,该环路的定制概率是随着相对适应度的增加而增加.而对于种群中相对适应度大于种群中原有个体的平均适应度,即该突变体是一个优势突变体时,环路的平均固定时间随着适应度的增加而减少,而环路的定置概率是随着相对适应度的增大而增大的.
[1] Lieberman E,Hauert C,Nowak M A. Evolutionary dynamics on graphs[J]. Nature,2005,433(20):312-316.
[2] Shakarian P,Roos P,Johnson A. A review of evolutionary graph theory with applications to game theory[J]. BioSystems,2012,107(2):66-80.
[3] Broom M,RychtT. Evolutionary dynamics on graphs—the effect of graph structure and initial placement on mutant spread[J]. The Journal of Statistical Theory and Practice,2011,5(3):369-381.
[4] Ohtsuki H, Hauert C, Lieberman E,et al. A simple rule for the evolution of cooperation on graphs and social networks[J].Nature, 2006,441(7092):502-505.
[5] Nie Puyan, Zhang Peiai. Evolutionary graphs with frequency dependent fitness[J]. Internal Journal of Modern Physics B,2009,23(4):537-543.
[6] Nie Puyan, Zhang Peiai. Fixation time for evolutionary graphs[J]. International Journal of Modern Physics B,2010, 24(27): 5285-5293.
[7] Zhang Peiai, Nie Puyan, Hu Daiqiang. Bi-level evolutionary graphs with multi-fitness[J]. IET Systems Biology,2010,4(1):33-38.
[8] Zhang Peiai.Fixation probabilities of evolutionary graphs bassed on the positions of new appearing mutants[DB/OL]. http://www.hindawi.com/journals/jam/2014/901363/2014-04-17.
[9] Nie Puyan. Evolutionary graphs on two levels[J]. Ars Combinatoria,2008, 86:115-120.
[10] Whigham P A, Dick G. Evolutionary dynamics for the spatial Moran process[J]. Genetic Programming and Evolvable Machines,2008, 9(2):157-170.
[11] Paley C, Taraskin S,Elliott S.Temporal and dimensional effects in evolutionary graph theory[J]. Physical Review Letters,2007,98(9):1-13.
[12] Antal T, Scheuring I. Fixation of strategies for an evolutionary game in finite populations[J]. Mathematical Biology,2006,68(2):1923-1944.
[13] 张京友,张培爱,钟海萍.进化图论在知识型企业组织结构中的应用[J].山东大学学报:理学版,2013,48(1): 107-110.
[14] Liang Dongfang, Wu Xuefei. A random walk simulation of scalar mixing in flows through submerged vegetations[J]. Journal of Hydrodynamics,2014, 26(3):343-350.
[15] 刘恒,寇月,申德荣,等.基于随机游走路径的分布式SimRank算法[J].计算机科学与探索,2014,8(12):1422-1431.
(责任编辑 李春梅)
Average Fixation Time on a Circulation
ZHANG Pei-ai
(Department of Mathematics, Jinan University, Guangzhou 510632, China)
Evolutionary graph can be used to describe the evolution of a population dynamically. The fixation probability of an evolutionary graph is the probability that a new emerging mutant occupies the whole population, while its average fixation time reflectes the average evolutinary velocity of the population. The average fixation time of a new mutant on a circulation with large population is studied and its property is discussed. When the relative fitness 0
circulation; average fixation time; evolution graph; fixation probability
1004-8820(2015)04-0246-03
10.13951/j.cnki.37-1213/n.2015.04.003
2015-05-13
教育部人文社科资助项目(11YJAZH118).
张培爱(1973- ),女,山东潍坊人,副教授,博士,研究方向为最优化理论及其应用.
O224
A

