属性粗糙集粗糙性的度量方法
郭志林,王 宁
(商丘师范学院数学与信息科学学院,河南 商丘 476000)
属性粗糙集粗糙性的度量方法
郭志林,王 宁
(商丘师范学院数学与信息科学学院,河南 商丘 476000)
考虑到粗糙集的不确定性与其所在近似空间知识粒度的关系,在属性粗糙集模型的基础上,将传统的粗糙度与知识粒度相结合,提出了一种新的属性粗糙集粗糙性的度量方法,讨论了这一度量的特性.证明了随着近似空间的细分新的粗糙度单调减小的性质.
属性粗糙集;属性测度;知识粒度;粗糙度
粗糙集理论作为一种处理不确定性知识的数学工具,在人工智能、模式识别、数据挖掘与信息处理等领域得到广泛应用. 建立在等价关系基础上的经典粗糙集理论极大地限制了其在实际的应用.为适应各种复杂系统的应用需要,对粗糙集模型的扩展成为当今研究的热点.随着理论研究的深入,粗糙集理论逐渐和其他数学理论如FUZZY集、VAGAU集、概率论和随机集等相结合,形成各种扩展的粗糙集模型[1-4], 将属性数学[5-7]引入到粗糙集理论,作者首次建立了属性测度空间的粗糙集模型[8], 并讨论了具有动态特性的S-属性粗糙集的性质[9-10].但发现,将Pawlak提出的近似精度和粗糙度等概念应用于属性粗糙集,虽然可以直观地反映属性粗糙集的不确定性,但当属性集的知识被逐渐细分时,属性粗糙集的粗糙度有时将不会变化,这不符合人们对不确定性问题的直观认识.由于属性粗糙集的不确定性除与它本身的粗糙性有关外,还与属性测度空间本身的不确定性有关.本文从属性测度空间的角度,讨论了不同粒度的近似空间(即不同层次的商空间)下属性粗糙集的粗糙度的变化情况,将Pawlak粗糙度应用于属性粗糙集,与不同近似空间的知识粒度相结合,提出了一种新的属性粗糙集的粗糙度,证明了这种粗糙度随着近似空间的细分而单调减小的性质,并举例说明这种度量方法克服了经典粗糙集粗糙度的局限性,与人们对不确定性问题的直观认知相吻合.
1 基本概念
定义1[5-7]设U为对象空间,X为属性空间(或最大属性集,X⊂U),属性空间X的任一子集A称为属性集.
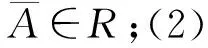
定义3[5-7]设x为X中的一个元素,A为一个属性集,μA(x)表示“x具有属性A”的程度,称为x∈A的属性测度(0≤μA(x)≤1).
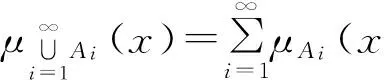

定义6 设U为对象空间,(X,R,μ(x))为属性测度空间.A是R上的一个属性集合,定义A关于(X,R,μ(x))的粗糙度ρR(A)为
.

显然,0≤ρR(A)≤1,0≤ηR(A)≤1.若A是可定义的,则ρR(A)=0,ηR(A)=1.
用属性粗糙集的粗糙度ρR(A)或近似精度ηR(A)来刻画属性粗糙集的不确定性具有一定的局限性.下面举例来理解这种局限性.
例1 设U={x1,x2,x3,x4,x5,x6,x7,x8,x9},A是U上的属性集,其属性测度μA(x)={0.4,0.6,0.4,0.6,0.2,0.6,0.4,0.8,0.9},即
对于U上的等价关系S1,S2,有
U/S1={{x1,x2,x3,x4},{x5,x6,x7},{x8,x9}},
U/S2={{x1,x2},{x3,x4},{x5,x6,x7},{x8,x9}}.


显然,知识S2比知识S1精细. 但属性集A在不同划分S1,S2下的粗糙度却相同. 因此,传统的粗糙度具有一定的局限性.
2 粒度意义下属性粗糙集的粗糙性度量

以P(A)表示属性集A的幂集,则在任意给定的信息系统S=(U,A,V,f)中,P(A)与包含关系⊆构成一个完备的偏序格
例2 设A={a1,a2,a3}, 则图1给出

图1 格
如Φ⊆{a1}⊆{a1,a2}⊆{a1,a2,a3},Φ⊆{a1}⊆{a1,a3}⊆{a1,a2,a3}和Φ⊆{a2}⊆{a1,a3}⊆{a1,a2,a3}等都是属性链.
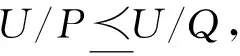

例3 设信息系统U={x1,x2,…,x10},属性集A={a1,a2,a3}, 如表1所示.

表1 信息系统
假若取属性链Φ⊆{a1}⊆{a1,a2}⊆{a1,a2,a3},可以得到如下的分层递阶近似空间:U/Φ={{x1,x2,…,x10}},U/{a1}={{x1,x2,x3,x4,x5},{x6,x7},{x8,x9,x10}},U/{a1,a2}={{x1,x2},{x3,x4,x5},{x6,x7},{x8},{x9,x10}},U/{a1,a2,a3}={{x1,x2},{x3,x4},{x5},{x6},{x7},{x8},{x9,x10}}.
说明在不同属性链的分层递阶的近似空间中,属性个数越来越多,知识颗粒越来越细.
定义8[12]设U={x1,x2,…,xn},属性集B(B⊆A)对论域U的划分U/B={X1,X2,…,Xn},则U/B的知识粒度定义为
定义8的知识粒度具有下列性质:
定理1 设格
GD(Bi+1)≤GD(Bi).
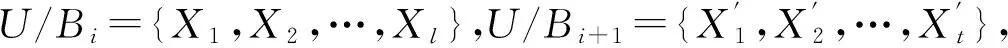
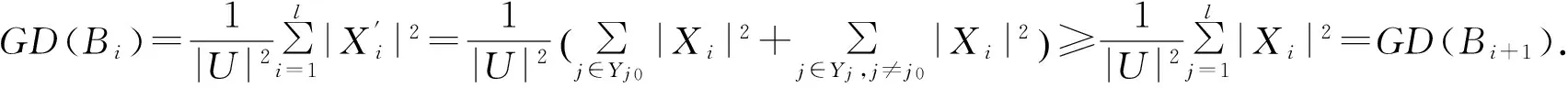
此定理说明在分层递阶近似空间中,随着属性个数的逐渐增加,知识粒度单调减小.
对于X⊆U,X的粗糙性不仅与其本身的粗糙性有关,还与论域U上知识的粗糙性有关,为此,引进属性粗糙集的粗糙度的概念.
定义9 设S=(U,A,V,f)是一个信息系统,U={x1,x2,…,xn},属性集R⊆A,Φ⊂X⊆U,则X的粗糙度定义为
RoughnessR(X)=ρR(X)GD(R).
新定义的粗糙度不仅考虑了集合X本身的粗糙性, 而且更进一步考虑了近似空间的相对知识粒度,从而能更真实的反映X的粗糙度.
定理2 设(X,R,μ(x))为属性测度空间,A为属性集,若S1⊆S2,则
RoughnessS1(A)≤RoughnessS2(A).
证明 因为S1⊆S2,所以[x]S1⊆[x]S2.从而∀x∈U,有

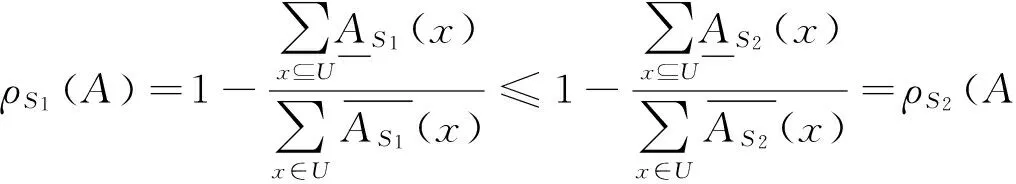
由定理1知,GD(S1)≤GD(S2),从而
RoughnessS1(A)≤RoughnessS2(A).
定理2说明属性粗糙集的粗糙度随着信息粒度的变小而单调减小.
下面通过实例来说明定理2的正确性.
例4 仍以例1为例,例1已经算得属性集A关于属性测度空间(X,R,μ(x))和(X,S,μ(x))的粗糙度ρR1(A)=ρR2(A)=0.367,但明显知识R1比知识R2粗糙. 应用新的粗糙度的度量公式,进一步计算, 由于
所以
RoughnessR1(A)=ρR1(A)GD(R1)=0.131,
RoughnessR2(A)=ρR2(A)GD(R2)=0.095.
说明划分越细,粗糙度越小,符合人们的直观认识.
3 结束语
粗糙集的不确定性由集合X本身及近似空间2个方面确定,将这2个方面合理地结合起来是解决粗糙集不确定性问题的有力工具.本文指出了Pawlak粗糙度在属性粗糙集粗糙性度量中的不足,将近似空间中的知识粒度与Pawlak粗糙度相结合,提出了属性粗糙集粗糙性的一种度量方法,并证明了新的粗糙度随着划分加细粗糙度变小这一结论.通过举例说明这种新的度量方法克服了Pawlak粗糙集粗糙度的局限性,为属性粗糙集的应用提供了理论依据.
[1] Dubois D, Prade H. Rough fuzzy sets and fuzzy rough sets[J]. International Journal of General Systems, 1990, 17: 191- 208.
[2] Morsi N N, Yak M M. Axiomatics for fuzzy rough sets[J]. Fuzzy Sets and Systems, 1998, 100: 327-342.
[3] 张淮中.Bayes决策的概率型粗糙集模型[J].小型微型计算机系统,2004,25(3):407-409.
[4] 张文修,吴伟志.基于随机集的粗糙集模型(I)[J].西安交通大学学报,2000,34(12):75-79.
[5] 程乾生.属性集和属性综合评价系统[J].系统工程理论与实践,1997,9:1-9.
[6] 程乾生.属性识别理论模型及其应用[J].北京大学学报:自然科学版,1997,33(1):12-20.
[7] 程乾生.属性数学——属性测度和属性统计[J].数学的实践与认识,1998,28(2):97-107.
[8] 郭志林.属性测度空间的粗糙集模型[J].模糊系统与数学,2009,23(2):162-166.
[9] 郭志林.双向S-属性粗糙集模型[J].山东大学学报:理学版,2010,45(12):117-121.
[10] 郭志林.双向S-属性粗糙集及其性质[J].山西大学学报:自然科学版,2010,33(4):513-518.
[11] 王国胤,张清华.不同知识粒度粗糙集的不确定性研究[J].计算机学报,2008,31(9):1588-1597.
[12] 解滨,李磊军,米据生.基于知识粒度的粗糙集的不确定性度量[J].计算机科学,2010,37(9):225-228.
(责任编辑 李春梅)
A New Method for Measuring Roughness of Attribute Rough Sets
GUO Zhi-lin, WANG Ning
(School of Mathematics and Information Science, Shangqiu Normal University, Shangqiu 476000, China)
Based on the fact that the uncertainty of rough sets is closely related to the knowledge granularities of the same approximation space, a new method for measuring the roughness of attribute rough sets is proposed by integrating the traditional roughness with knowledge granularities. We discuss the properties of this measure and prove that this new roughness is decreasing with the refinement of knowledge granularities in approximation space.
attribute rough set; attribute measure; knowledge granularity; roughness measure
1004-8820(2015)04-0235-04
10.13951/j.cnki.37-1213/n.2015.04.001
2015-01-08
国家自然科学基金资助项目(61179038); 河南省自然科学基金资助项目(132300410391).
郭志林(1963- ),男,回族,山东曹县人,教授,研究方向为粗糙集理论及应用.
O159
A

