确定专家权重的数量积法及在排名中的应用
郭东威,丁根宏,毛俊诚,陈玉磊
(1.河海大学理学院,江苏 南京 211100;2.北京科技大学数理学院,北京 100083)
确定专家权重的数量积法及在排名中的应用
郭东威1,丁根宏1,毛俊诚1,陈玉磊2
(1.河海大学理学院,江苏 南京 211100;2.北京科技大学数理学院,北京 100083)
对群决策及残缺主观评价系统研究分析,发现直接对评分取均值排名会因专家打分尺度的不同带来较大误差,虽然T分数法可以将打分尺度统一,但是缺乏对专家评价对象不同的考虑.为减小此系统误差,提出了一种确定专家权重的数量积法,并将其应用于论文型竞赛排名系统.与传统方法及T分数法比较,对T分数求加权平均值排名,提高了主观名次与客观名次的重合度,减小了其乱序度.计算欧氏距离,证明新方法减小了评委打分的误差度及论文的争议度.
主观评价;数量积;权重;残缺评分矩阵;系统误差
在群决策中,尤其是主观评价系统,专家权重起着至关重要的作用,它直接影响着决策的结果.专家权重可分为先验权重和后验权重[1].先验权重由相关的先验信息(如历史数据)计算得出,是对专家知识、经验、能力、水平、期望及偏好等的综合数量表示.确定先验权重常用的方法有AHP法、Delphi法、利用互评的方法[2-3]、夏普利—舒笔克权力指数法[4]、班扎夫权力指数法[4]等.后验权重是将专家决策结果与实际比较,确定前者相对于后者的偏离程度,通过反馈信息、逆判进行赋权.确定后验权重的方法有利用均衡指标CHI的方法[5]、利用一致性指标的方法[2]、最大特征值方法[6]、导出矩阵的方法[6]、相似度函数方法[7]、信息熵的权力指数法[3]等.此外,Patrik Eklund等[8]研究了满足共识度和规模度的群决策中专家交互过程问题[8].已有的方法侧重点各有不同,涉及具体问题时可根据各方法的特点采用一种或多种方法来考查问题.群决策论文型竞赛名次问题是一类主观评价性问题,由于各评委打分习惯及把握评分标准的不同,使得决策误差较大.目前已有不少专家学者对此问题做了深入的研究,比如T分数法[9],基于神经网络技术的评卷模式[10],对残缺数据进行填补[11-12]等.本研究在前人研究的基础上,提出了确定专家权重的数量积法,通过论文型竞赛排名的模拟试验,证明该权重可以有效减小此类决策的误差,增强了决策的科学性准确性.
1 确定专家权重的数量积法


2 在论文型竞赛排名中的应用
2.1 论文分配模型
在大型竞赛中,比如全国大学生数学建模竞赛,由于工作量、时间等原因,每位评委不能评阅每份论文.为使决策公平公正科学化,只能在某种最优准则下,每篇论文由随机的几个评委逐一评分.因此,评分矩阵A=(aij)m×n是残缺不全的,残缺部位可用0填充.
设共有参赛论文n份,随机编号为1-n;评委m位,随机编号为1-m.每份试卷由t位评委评分.
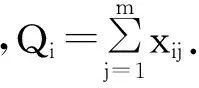
论文分配的数学模型:
目标函数 min{z=(maxQi-minQi)} .
目标函数说明:使得任意2个评委所评阅论文的数量尽可能接近.


2.2 常用排名方法简介
方法1(传统方法): 直接对各篇论文的原始得分取平均值进行排名.
方法2(T分数法): 将原始评分按公式(1)转换后的分数bij称为T分数,依据T分数均值对论文排名的方法称为T分数法.
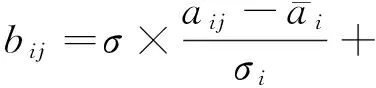
(1)
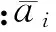
2.3 评委权重及竞赛名次的确定
假设:(1) 每个评委都有较高的评阅水平,即他对一组论文进行排名应和该组论文的真实排名不会出现严重不合,误判情况除外.(2) 每个评委都是公正的,即如果他认为论文A优于论文B,则应有A的分值大于B的分值.
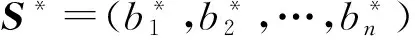
3 模拟试验及对比分析
3.1 成绩的生成
统计资料表明,在大型竞赛中,考生总体成绩合理有效的分布应该呈对称正态分布或正偏态分布,因此本文所做的100次模拟试验中,论文的客观成绩、各评委所打的分数均服从正态分布,具体操作如下.

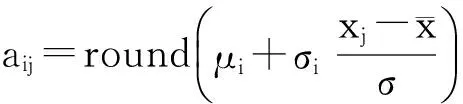
3.2 检验排名结果好坏的指标
定义1 主观名次:一篇论文依据评委的打分排名得到的名次称为主观名次.第j篇论文的主观名次记为tj,其客观名次记为pj.
定义2 重合度:主观名次与客观名次相同的个数称为重合度,用C表示.显然,重合度越大越好.
定义3 乱序度: 每篇论文的主观名次与其客观名次之差的绝对值的和称为乱序度,用D表示.则
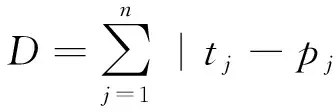
显然,乱序度越小越好.
3.3 对评委评分误差度及论文争议度的分析
考查评委评分的误差度及论文的争议度,可以引入欧氏距离来测度,即对第i号评委,有
(2)
对第j篇论文,有
(3)

3.4 具体试验及结果分析
取论文数量n=40,评委数m=5,进行随机模拟N=100次试验,并将本文方法的结果与排名方法1、方法2的结果作比较,具体见表1.为方便起见,以下称本文方法为方法3.

表1 100次试验结果
从表1可以明显看出方法3的排名效果要优于方法1与方法2,说明评委权重大大优化了排名的结果.
下面给出其中的一次试验,具体数据及3种方法的排名结果见表2,评委权重见表3,3种排名方法的结果比较见表4.由表2可以知道每位评委评阅论文24份,说明了本文给出的论文分配模型的可行性.由表2、表4不难看出方法1的排名效果最差,而且容易出现得分相同的现象;方法2和方法3在最终的得分上有1分左右的差别,这是由于不同评委所评阅的论文水平的差异引起的,由权重予以修正的方法3的排名结果要比方法2更科学.
图1、图2分别利用式(2)、(3)的分析模型,比较了3种排名方法的结果,显然新方法明显降低了评分误差度,提高了评委的准确度,减小了论文的争议度,因此排名结果更科学合理.
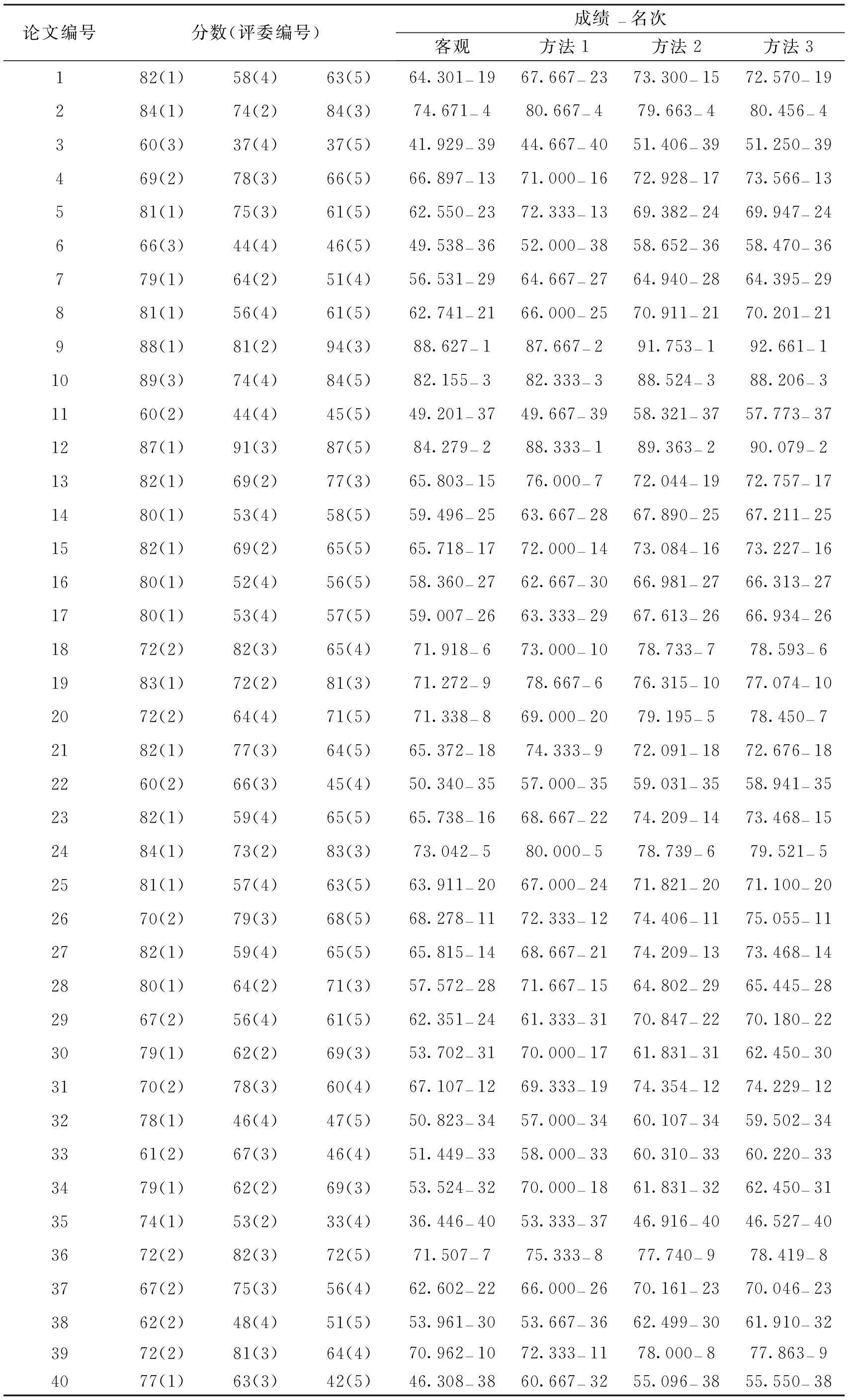
表2 成绩及名次
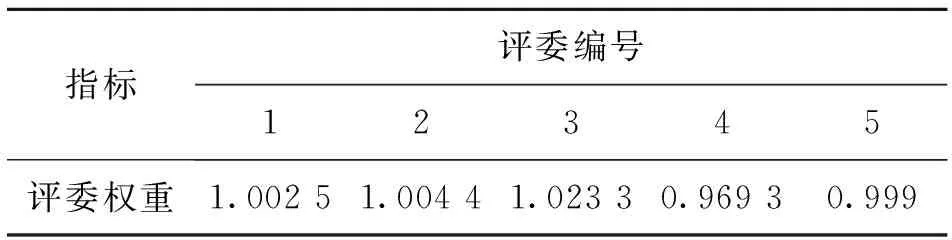
表3 评委权重

表4 结果比较

图1 评分误差度比较
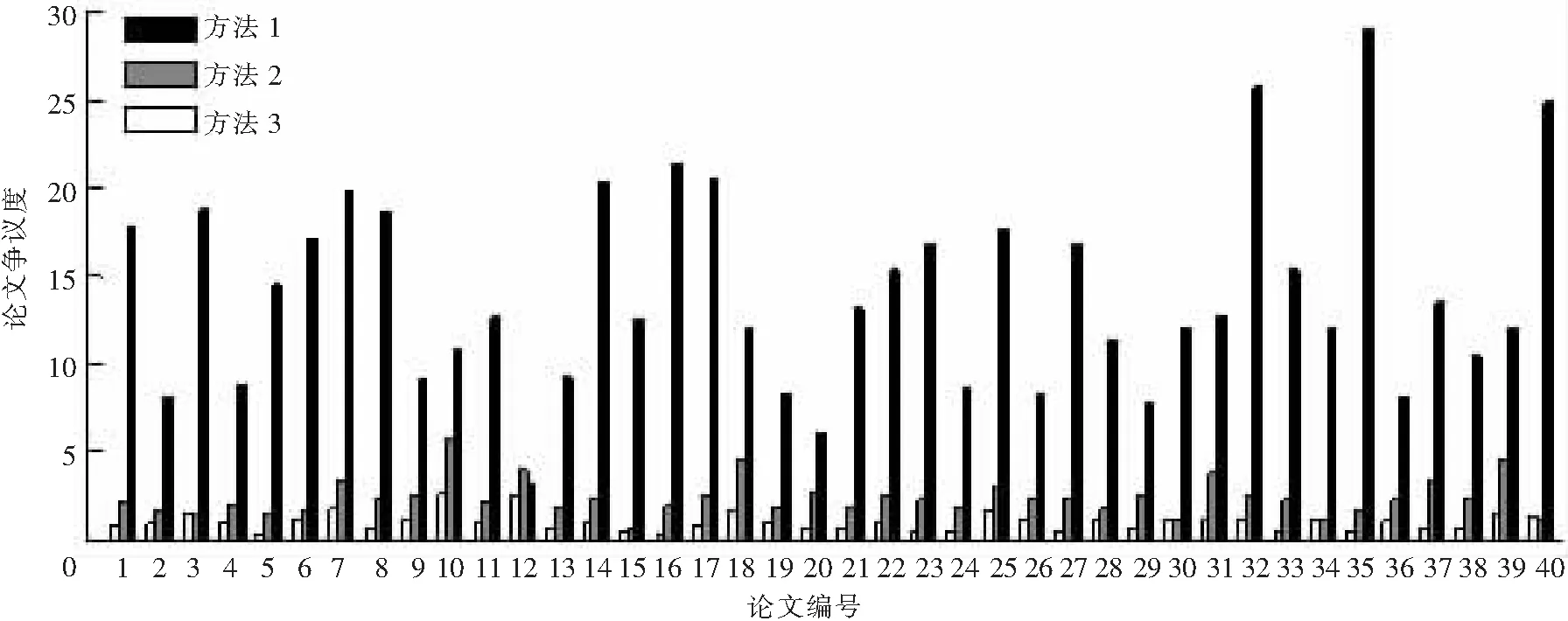
图2 论文争议度比较
4 结束语
合理确定专家的权重,可以有效提高决策的科学性准确性.通过对群决策及主观评价系统的研究分析,笔者发现,在主观评分系统中专家权重的大小主要反映的并非专家权威的大小,而是专家评分的习惯.比如对于被评对象A与B,甲专家评分可能为65和80,而乙专家评分可能为45和60,但这并不影响决策的结果.在大型评价系统中,被评对象就有很多,即使各专家都有相当高的评估水平,也难免出现意见不同的情况.若直接取均分,由于存在专家评分高低不等的系统误差,使得决策结果误差较大.因此,确定专家权重的一个重要原则就是在不改变评价对象在各评委心目中的地位的前提下,增加权重后使得各专家的意见(或评分)尽可能接近,以减小评分系统误差及争议,再取均值.本研究基于该原则提出了确定专家权重的数量积法,通过论文型竞赛排名试验,证明了该方法提高了主观评价系统的科学性准确性,有较强的适应性.
[1] 周宇峰,魏法杰.一种综合评价中确定专家权重的方法[J].工业工程,2006,9(5):23-27.
[2] 刘进生,王庆云,张福伟.列和求逆法的保序性及群体权重计算[J].系统工程理论方法应用,1993,2(3):69-72.
[3] Ramanathan R, Ganesh L S. Group preference aggregation methods employed in AHP: An evaluation and an intrinsic process for deriving members′ weightages[J]. European Journal of Operational Research, 1994, 79(2): 249-265.
[4] 杨雷.群体决策理论与应用——群体决策中的个体偏好集结方法研究[M].北京:经济科学出版社,2004:117-130.
[5] 韩旭里,李松仁.基于一致性均衡权指标的排序方法[J].系统工程理论方法应用,1994,3(1):41-45.
[6] 宋光兴,邹平.多属性群决策中决策者权重的确定方法[J].系统工程,2001,19(4):85.
[7] His-Mei Hsu, Chen-Tung Chen.Aggregation of fuzzy options under group decision making[J].Fuzzy Sets and Systems, 1996,79(4):278-285.
[8] Eklund P, Rusinowska A, De Swart H. Consensus reaching in-committees[J].European Journal of Operational Research, 2007,178(1):185-193.
[9] Klein J. Assessing university students’ achievements by means of standard score (Z score) and its effect on the learning climate[J]. Studies in Educational Evaluation, 2014, 40: 63-68.
[10] 丁文,杨卫东,刘继来.基于神经网络技术的评卷误差控制模型及其应用[J].浙江工业大学学报,2003,31(4):419-423.
[11] 易昆南,梁霞,易芳.残缺评分矩阵的论文排名[J].铁道科学与工程学报,2008,5(3):93-96.
[12] 易昆南.残缺数据的论文名次及评委水平的评判与逆判[J].湘潭大学自然科学学报,2005,27(2):39-43.
[13] 叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社,2006:29-45.
[14] Forman E, Kirti P.Aggregating individual judgments and priorities with the analytic hierarchy process[J].European Journal of Operational Research, 1998,108(1):165-169.
[15] Herrera F, Herrera-Viedma E, Chiclana F.Multiperson decision-making based on multiplicative preference relations[J].European Journal of Operational Research,2001,129(2):372-385.
[16] Chiclana F, Herrera F, Herrera-Viedma E. Integrating three representation models in fuzzy multipurpose decision-making based on fuzzy preference relations[J].Fuzzy Sets and Systems,1998,97(1):33-48.
(责任编辑 李春梅)
Dot Product Method for Determining Experts’ Weights and Application in Ranking
GUO Dong-wei1, DING Gen-hong1, MAO Jun-cheng1, Chen Yu-lei2
(1.College of Science, Hohai University, Nanjing 211100, China; 2. School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China)
In the analysis of group decision making and incomplete subjective evaluation system, we find that taking the means ranking directly brings big error due to the difference of experts’ scoring scales. Although the T-score method can be used to unify them, it lacks the difference of experts’ evaluation objects. In order to reduce this system error, in this paper, we propose the Dot Product method for determining experts’ weights and apply it to the theses type competition ranking system. Compared with the traditional and T-score methods, this method improves the coincidence of the subjective and objective ranking, and reduces the disorder degree. By calculating the Euclidean distance, we prove that the new method can reduce the experts’ scoring error and the controversy of theses.
subjective evaluation; Dot Product; weight; incomplete score matrix; system error
1004-8820(2015)04-0249-06
10.13951/j.cnki.37-1213/n.2015.04.004
2015-04-08
中央高校业务费资助项目(B12020128).
郭东威(1986- ),男,河南开封人,硕士研究生.
丁根宏(dinggenhong@126.com),副教授,博士,研究方向:运筹学优化与控制.
O29
A

