警用某型九管发射器振动模态分析

商保利，战仁军，商 鹏，张洪彪

(武警工程大学装备工程学院，陕西西安710086)

1 引 言

九管发射器(图1)是武警常用的车载非致命防暴武器，可用来发射38 mm催泪弹、防暴弹、烟雾弹、布袋弹等不同弹体，发射距离在100 m以上。该武器可以使人员短时间内失去抵抗能力，其强大的威力不仅适用于快速制止、驱散非法集会，打击流氓团伙斗殴等聚众闹事活动，更能很好地适用于武装巡逻、缉毒缉私、防暴搜捕、平息武装叛乱等任务。其和单兵使用的防暴枪相比，具有发射距离远、发射精度高、发射速度快的特点。其在处置大规模群体性事件中发挥着重要作用，是武警部队维护社会稳定的一种大威力的防暴非致命武器。

发射器在发射时受到固有频率、发动机转速、发射频率以及不同路况等因素的影响，其发射管往往会发生弯曲振动甚至产生共振。而这些振动会直接影响射击的精度和系统的可靠性。因此，有必要对发射器进行振动模态分析，获取发射器的固有频率，尽量避免共振的发生，为发射管的优化设计和改进提供合理的依据。

有限元方法是求解复杂物理数学问题的重要方法，能够对复杂的结构进行数值模拟。有限元方法(FEM)的基础是变分原理或加权余量法，其基本求解思想是把计算域划分为有限个互不重叠的单元，在每个单元内，选择一些合适的节点作为求解函数的插值点，将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式，借助于变分原理或加权余量法，将微分方程离散求解。有限元方法最早应用于结构力学，后来随着计算机的发展慢慢用于流体力学的数值模拟。有限元方法已经广泛应用于军事装备的建模仿真。其中吴东亚对某型坦克炮身管进行了模态分析［1］。张海航进行了多管火炮的模态分析［2］。但由于之前部队对非致命武器射击精确度要求较低，大家忽略了对非致命武器动力学的研究。这就在一定程度上造成了弹药的浪费。近几年，随着暴骚乱等群体性事件的增多，非致命武器的适用范围也越来越广。这就要求必须提高非致命武器的射击精度。既能实现有效打击又可以避免不必要的浪费。

所以本文以武警常用的车载九管发射器为研究对象，以有限元方法为理论支撑，以CAD软件Pro/E和大型常用的有限元软件ANSYS 13．0为工具，对发射器的振动模态进行分析，获取发射管的固有频率，为进一步进行动力学研究奠定基础。

2 振动对发射稳定性的影响

在武器发射的过程中，发射管的振动情况会增大弹着点的散布。在发射瞬间由于受到后坐力的影响发射管会产生俯仰运动。这样就会影响下一发弹的起始扰动，进而影响射击精度。同时，如果车辆在较为复杂路面行驶，会引起车体的振动。若车体的振动频率和发射管的固有频率相同或相近，就极易引起共振。发射管的振动阶数越低，对发射器射击精度的影响就会越大。

2.1 静止发射时的振动激励

静止发射时，振动的激励来自于弹体发射的后坐力。在各方向分力的作用下，发射管产生不同方向的振动。若采用连发模式，第一发弹发射带来的振动会对第二发弹的初始扰动带来影响。第二发的发射时间应避开第一发弹引起振动的最大振幅或者发射时间相差半个振动周期。

若采用多管齐发模式，管数不同则后坐力的大小不同，总的后坐力是各单管发射后坐力的矢量叠加。由于在不同大小的激励作用下产生的振动频率不同，如果某个振动频率ωj(j表示发射管的数目)和发射器的固有频率ω0相同或者相近，极易引起共振。

2.2 车辆行进时的振动激励

车辆行进过程中，发射器的振动主要来自于路面不平所带来的激励。激励通过轮胎、车架、悬架、车体的传递，作用于发射器，引起发射器的振动。以平均速度u通过路程为l的时间t=l/u，以平均速度通过波长为λ的路面时间T=λ/u为周期。T的倒数f=1/T=u/λ为频率［3］。

路面不平度的时间频率单边功率密度函数为

由于T=l/u，故有

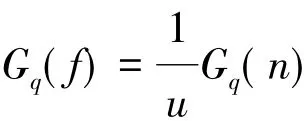
国际标准建议路面的空间频率谱用下式拟合

故得到路面不平度时间频率的单边谱的拟合式为

3 建立发射器的有限元模型

由于九管发射器(图1)的结构比较复杂，很难实现在ANSYS中直接建模，所以首先在Pro/E中建立物理模型，然后将其导入ANSYS中进行分析。

图1 九管发射器模型Fig．1 Model of nine pipe launcher

由于结构的固有频率和模态振型主要取决于质量分布和刚度，细节的影响不大。因此在建立三维数字化模型时，在不影响计算精度的前提下，适当对模型进行简化，忽略倒角、圆角、螺纹孔等不必要的细节。

发射器的整体结构过于复杂，而发射管对整个发射器的固有频率起着主导作用，因此只对发射管进行模态分析。根据发射管的实际尺寸在Pro/E中建立发射管的三维数字化模型(图2)。然后利用接口将模型导入ANSYS的仿真平台。整个模型采用8节点的solid185单元，它可模拟几乎不可压缩的弹塑和完全不可压缩的超弹。采用smart size的方法对模型进行智能网格化分。划分后整个模型共有单元45 134个，节点23 446个。得到有限元模型如图3所示。

图2 三维数字化模型Fig．2 Three-dimensional digital model

图3 有限元模型Fig．3 Finite element model

发射管的本质模型是一个悬臂梁结构，所以在发射管的后端施加全约束，根据物理属性对模型进行参数设置。发射管材料为钢，其几何参数、材料属性由有关技术文件获得。主要参数如表1所示。

表1 发射管模型的结构尺寸和材料参数［4］Tab．1 Structure dimensions and material parameters of launch pipe model

根据材料参数对模型进行材料参数相关设置。

4 模态计算及分析

模态分析理论吸取了振动理论、信号分析、数据处理、数理统计及自动控制中的有关“营养”，结合自身发展形成了一套独特的理论。模态分析技术已经广泛地应用在航天、航空、机械、造船、建筑、交通和兵器等工程领域。

模态分析的方法主要有两种，一种是用有限元方法计算获得，这种方法为数值模态分析。另外一种是通过实验获得采集信号和模态参数，这种方法为试验模态分析。数值模态分析是将弹性结构离散为有限个单元，根据单元的质量和弹性特征在计算机上完成相关数学理论运算。通过这种方法，可以在产品生产出来之前对其性能进行模拟，获得产品的相关模态参数，根据获得的数据对产品进行优化，可以缩短生产周期，降低生产成本［5］。本文采用此种方法进行分析。

4.1 模态计算数学模型

根据达朗贝尔原理，对于一个有N个自由度的线性系统，其运动微分方程为:

根据达朗贝尔原理，对于一个有N个自由度的线性系统，其运动微分方程为:

(1)模态分析:F(t)=0。

(2)谐响应分析:F(t)为周期载荷。

(3)瞬态动力学分析:F(t)为冲击载荷。

(4)谱分析:F(t)为随机载荷。

振动有F(t)=0，上式可以写为:

若忽略阻尼影响，即C=0则可进一步简化为:

式中:［M］为质量矩阵;［C］为阻尼矩阵;［K］为刚度矩阵;［X］为位移向量;{F(t)}为作用力向量;t为时间。

自由振动时各节点得的位移为:

其中:［Xmax］为位移振幅向量。

由式(3)、式(4)得:

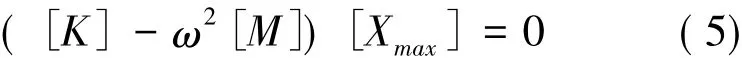
式(5)是齐次方程，要想得到［Xmax］的非零解，只能使系数矩阵的行列式为0，即

由此式，可求出n个特征值和他们分别对应的特征向量。其中特征值的平方根 ωi(i=1，2，…，n)就是结构的第i阶固有频率，特征向量［］就是第i阶的模态振型，它反映了结构按频率ωi振动时各自由度方向振幅间相对比例关系。［6－7］

4.2 模态仿真计算

在有限元模型建好后，进入solution求解器，选择分析类型为Modal。在ANSYS 13．0中，软件提供了 Block Lanczos，Subspace，Power dynamics，缩减法，不对称法，阻尼法6种模态提取方法。在选用提取方法时要根据模型的大小、计算机的运算能力等具体情况来定。Block Lanczos和其他的几种方法相比计算速度更快，适合于大型对称矩阵特征向量的求解，能使大部分问题得以解决，而且具有很高的精度，故本文采用此方法进行提取。在这里对发射管的前12阶模态进行提取，在“No．of modes to extract”中输入模态提取数目为12，在“No．of modes to expand”中输入模态扩展数目为12。

运用solution求解器进行求解，通过计算得到了模型的前12阶振动模态。由于低阶模态对发射精度有较大影响，高阶模态影响较小，所以在这里只分析1阶到6阶模态，可以得到模型的固有频率和振型如表2所示。

表2 各阶频率和振型Tab．2 Frequencies and vibration

同时，各阶的振型图如图4到图9，图中的位移仅表示振型，并非实际的位移大小。

图4 一阶模态振型Fig．4 1st modal shape

图5 二阶模态振型Fig．5 2nd modal shape

图6 三阶模态振型Fig．6 3rd modal shape

图7 四阶模态振型Fig．7 4th modal shape

4.3 结果分析

通过结果可以看出发射管的自由振动频率分布在1 000Hz至1 500Hz之间，在使用过程中为避免共振，确保发射精度，必须尽量避开这一频率。而对其振动产生影响的因素主要有发动机的频率、弹体的发射频率和路面的激励。

图8 五阶模态振型Fig．8 5th modal shape

图9 六阶模态振型Fig．9 6th modal shape

(1)发动机的转速通常在1 000～2 000 r/min，也就是振动频率在 16．7～33．3 Hz［8］，与发射器固有频率相差较大，不会产生共振，对发射精度的影响较小。

(2)在行车过程中，假设最高车速为80 km/h，路面不平度的最小波长为0．32(表3)。由于路面不平所带来的激励频率为:在公路上行驶的激励一般在15 Hz以下，在越野状态下，路况较差，其产生的激励也一般在50 Hz以下。与发射器固有频率相差较大。

表3 路面的不平度波长［9］Tab．3 Pavement roughness wavelength

(3)弹体的发射周期为10 s左右，频率在0．1 Hz，对发射影响较小。弹体的初速度为70 m/s，在发射管内的飞行时间为 0．004 3 s［10］。而发射管的振动周期为 0．000 67～0．001 00 s。弹体的飞行时间避开了振动周期的1/2，即振幅的最大值，避免了共振的产生。

5 结 语

(1)本文通过模态分析获得了发射管的固有频率，分析了其可能产生共振的环境以及避免共振的措施，为下一步发射管的动力响应分析提供了数据和技术基础，具有可借鉴意义。

(2)以武警常用九管发射器为切入点，进行动力学分析，在一定程度上弥补对非致命武器动力学研究不足的现状，为其他车载非致命武器的系统动力学分析提供了思路和方法。

(3)本文只是获得了发射器的固有频率。不能很好地模拟其在整个发射过程的瞬态响应情况。影响发射器发射精度的因素较多，需要在日后进行进一步研究。

［1］ 吴东亚，刑宏光．基于有限元的某型坦克炮身管模态分析［J］．科技导报，2008，26(23):44－47．WU Dongya，XING Hongguang．Modal analysis of a tank gun barrel based on finite element method［J］．Review of Science and Technology，2008，26(23):44－47．

［2］ 张海航，狄长安．某型多管火炮的振动模态分析［J］．兵工学报，2008，12(29):1514－1516．ZHANG Haihang，DI Changan．Analysis of vibration modal of a multibarrel cannon［J］．Acta Armamentaria，2008，12(29):1514－1516．

［3］ 毛保全．车载武器发射动力学［M］．北京:国防工业出版社，2010．MAO Baoquan．Launching dynamics of vehicle weapon［M］．Beijing:National Defense Industry Press，2010．

［4］ 曾正明．机械工程材料手册［M］．北京:机械工业出版社，2010．ZENG Zhengming．Handbook of mechanical engineering materials［M］．Beijing:National Defense Industry Press，2010．

［5］ 袁安富，陈俊．ANSYS在模态分析中的应用［J］．设计与研究，2007(8):79－81．YUAN Anfu，CHEN Jun．Application of ANSYSin model analysis［J］．Design and Research，2007(8):79－81．

［6］ 傅志方，华宏星．模态分析理论与应用［M］．上海:上海交通大学出版社，2000．FU Zhifang，HUA Hongxing．Theory and application of modal analysis［M］．Shanghai:Shanghai Jiao Tong University Press，2000．

［7］ 徐立黄，张贵林．基于有限元的某多管火箭炮模态分析［J］．弹箭与制导学报，2010，6(30):110－115．XU Lihuang，ZHANG Guilin．The modal analysis of a MLRS based on FEM ［J］．Journal of Projectiles，Rockets，Missiles and Guidance，2010，6(30):110－115．

［8］ 喻凡，林逸．汽车系统动力学［M］．北京:机械工业出版社，2005．YU Fan，LIN Yi．Dynamics of vehicle system［M］．Beijing:Machinery Industry Press，2005．

［9］ 梁君，赵登峰．模态分析方法综述［J］．现代制造工程，2006(8):139－141．LIANG Jun，ZHAO Dengfeng．Summary of method modal analysis［J］．Modern Manufacturing Engineering，2006(8):139－141．

［10］ 赵陕冬，马永忠．非致命武器与警用器材［M］．北京:兵器工业出版社，2005．ZHAO Shandong，MA Yongzhong．Nonlethal weapons and police equipment［M］．Beijing:Weapon Industry Press，2005．