基于粒模型的PAD情感模型描述方法

林君焕，陈月芬

(1．台州职业技术学院 机电学院，浙江台州318000;2．台州学院物理与电子工程学院，浙江 台州318000)

1 引 言

PAD情感模型可以对情感进行有效的描述。它可以将人类的抽象情感映射到由P，A，D三个维度构成的空间里，并通过三个维度坐标来实现特定情感的量化表达，其中三个维度的具体涵义为:愉悦度(Pleasure)代表个体情感状态的正负特性，激活度(Arousal)代表个体的神经生理激活水平，优势度(Dominance)代表个体对情景和他人的控制状态。PAD三维情感模型作为情感与计算之间的桥梁，具有很强的可操作性，便于计算机的处理。

原有PAD情感模型存在几个问题:① 人类情感丰富细腻，复杂情感可能由2个以上基本情感合成。②人在认知情感时，可能会从不同层面上去获取有关情感知识，如宏观层面上来说，情感总的可以分成消极情感和积极情感，往下一层可以进一步将积极情感分成高兴、轻松等，消极情感可以分为害怕、发怒等。如何在PAD情感空间里对情感进行不同层面的描述，是情感计算的关键之一。

基于此，本文通过基于商空间理论的粒模型与方法来描述PAD情感模型，并最终能够在一定程度上解决如上所述的一系列情感计算问题。

2 粒的基本概念

定义1 设U是非空有限集合，称之为论域。P(U)为论域U的幂集，U上的一个等价关系R:U→P(U)。由R在U上产生一个划分U/R={［u］R/u∈U}={U1，U2，Ui，…，Um}，称为 R 的等价类或基本集，U1，U2，Ui，…，Um称为 R 的粒［1］。且满足:

(1)UiU，Ui≠φ

(2)Ui∩Uj=φ，i≠j，i，j=1，2，3，…，m

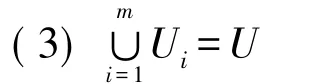
定义2 定义R的粒度［2］为

式中:当定义1中U为离散论域时，A 表示A的基数，当U为连续论域时，A =∫Ad x，下同。

定理1 设R在U上的一个等价关系，其产生的划分 U/R={U1，U2，…，Um}，则有

证明略。

性质1 设R是U上的一个等价关系，则有

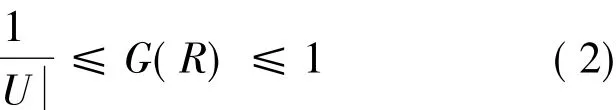
证明 当R是相等关系时，即R=ω时，R的粒度最小论域关系，即R=σ时，R的粒度最大，G(R)=

定义3 设R是论域U上的一个等价关系族，且 R1，R2∈R，若对 x，y∈U，xR1yxR2y，则称R1比 R2细，记为 R1R2。

性质2 设R1，R2是论域U的两个等价关系，且 R1R2，则 G(R1)＜G(R2)。

定义4 设R是U上的一个等价关系，R在U上产生一个划分U/R={U1，U2，…，Um}，则 R 在 U的子集构成的σ－代数上定义的概率分布为［3］

定义5 设R是U上的一个等价关系，U/R={［u］R/u∈U}={U1，U2，Ui，…，Um}，定义 R 的信息熵H(R)为

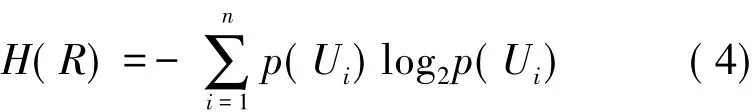
信息熵也是R对论域U进行划分的粗细程度的衡量。

性质3 当R由最粗的论域关系到最细的相等关系时，H(R)由0增大到log2U。

证毕。

3 基于商空间的粒

3.1 商空间模型

定义6 设U为所要研究的论域，在U上有属性函数f:U→W，其中W可以是多维的，各维既可以是实数域，也可以是其他的集合。拓扑T用来描述U中各元素之间的关系，则称三元组(U，f，T)为所要研究的对象［4］。

定义7 设R是U上的一个等价关系，则由R产生的划分构成U的一个商集［U］。在［U］上定义的商拓扑［T］为［T］={u/p－1(u)∈T，u∈［U］}，其中，p:U→［U］是自然投影;p－1是 p的逆变换。在［U］上构造出属性函数［f］，则称三元组(［U］，［f］，［T］)为(U，f，T)的商空间［4］。

3.2 模糊商空间理论

定义8 设U是论域，U上的一个模糊集A是指u∈U，有-μA∈［0，1］，称为 u对 A 的隶属程度，映射 μA:U→［0，1］，u→μA(u)称为 A 的隶属函数［5］。

令F(U)表示U的模糊子集的幂集，则F(U)实际上是由 μAi:U→［0，1］，Ai∈F(U)，i=1，2，3，…组成的函数族。

定义 9 设 R∈F(U×U)，若满足［5］:

(1) u∈U，R(u，．u)=1

(2) u，v∈U，R(u，．v)=R(v，．u)

(3) u，v，w∈U，R(v，．w)≥

supu(min(R(v，．u)，R(u，．w)))

则称R是U上的一个模糊等价关系。

命题1 设R是U上的一个模糊等价关系，若u，v∈U，R(u，v)=1，则称是 U 上的一个普通等价关系，可令由构造的对应商空间为［U］［5］。

命题2 设R是U上的一个模糊等价关系，令 Rλ={(u，v)/R(u，v)≥λ}，0≤λ≤1，则 Rλ是U上的一个普通等价关系，称Rλ为R的截关系，令由 Rλ构造的对应商空间为 U(λ)［5］。

定义10 设R是U上的一个模糊等价关系，Rλ为R的截关系，Rλ构造的对应商空间为U(λ)={U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)}，则称U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)为 Rλ的粒。

定义11 根据定义2和定义10，Rλ的粒度定义为

式中:当定义9中U为离散论域时，A 表示A的基数，当U为连续论域时，A =∫Ad x，下同。

定理2 设R是U上的一个模糊等价关系，Rλ为R的截关系，且由Rλ构造的对应商空间为U(λ)={U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)}，则有

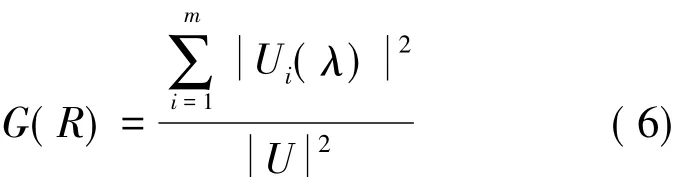
证明 由定理1同理可得。

性质4 设R是U上的一个模糊等价关系，Rλ是 R 的截关系，则有 0≤λ2≤λ1≤1Rλ1＜Rλ2U(λ2)是 U(λ1)的商集。于是商空间族{U(λ)/0≤λ≤1}按照商集的包含关系构成一个有序链，称{U(λ)/0≤λ≤1}为U上的一个分层递阶结构［5］。

性质5 设R是U上的一个模糊等价关系，Rλ1，Rλ2是 R 的截关系，且有 Rλ2＞Rλ1，则有 G(Rλ1)＜G(Rλ2)。

命题3 给定一个U上的模糊等价关系，则对应一个U上的分层递阶结构［5］。

定义12 设R是U上的一个模糊等价关系，可得到一个与它等价的U的商空间［U］上的归一化等腰距离d。对a∈［U］，定义μa(b)=1－d(a，b)，b∈［U］。那么每个 μa就定义了［U］上一个模糊集。由这些模糊集构成的空间就对应于模糊等价关系R的模糊商空间{μa/a∈［U］}，或称其为U上的一个模糊知识基。注:U的商空间［U］上的归一化等腰距离的相关概念见文献［5］。

定义13 设R1，R2是U上的两个模糊等价关系，若对(u，v)∈(U×U)，有 R1(u，v)≤R2(u，v)，则称 R2比 R1细，记为 R1≤R2。

定理3 在上述定义的关系“＜”下，所有U上的模糊商空间全体构成一个完备半序格R［5］。

证明略。

4 PAD情感空间的粒模型

PAD空间中的三个坐标轴具体量值含义为:+P代表愉悦，－P代表不愉悦;+A代表激活，－A代表不激活;+D代表优势，－D代表没有优势，每个维度上的数值范围为［－1，+1］，－1表示该维度上的值比较低，相反+1表示该维度上的值比较高，例如希望的坐标是(0．2，0．2，－0．1)。通过这种量化表示，OCC(由 Ortony，Clore，Collins三位学者提出的情感模型，称为OCC模型，在该模型中，他们根据不同的情感刺激提出了22类情感)中的情感类型与PAD三维情感模型的对应关系［6］如表1所示。

将PAD空间的情感状态通过粒模型来描述，首先是将P，A，D三维坐标构成的空间作为所要研究的对象论域。该论域由表1中的24个离散情感状态构成。

定义14 设PAD情感空间论域为U:P×A×D，在U:P×A×D 上有属性函数f:P×A×D→E，E 为情感状态空间。拓扑T是U:P×A×D上各元素之间的关系。则(U，f，T)就是PAD情感空间上所要研究的对象。

定义15 设R是U:P×A×D上的一个等价关系，则由R产生的划分构成U:P×A×D的一个商集［U］。在［U］上定义的商拓扑［T］为［T］={u/p－1(u)∈T，u∈［U］}，其中，p:U→［U］是自然投影;p－1是p的逆变换。在［U］上构造出属性函数［f］，则称三元组(［U］，［f］，［T］)为(U，f，T)的PAD情感商空间。

定义16 设R∈F(U×U)，若满足:

(1) u∈U，R(u，．u)=1

(2) u，v∈U，R(u，．v)=R(v，．u)则称R是U上的一个模糊相似关系。

表1 OCC情感类型与PAD三维情感模型的对应关系Tab．1 Corresponding relationship between emotions of OCC and the 3-dimension emotional model of PAD

定理 4 令 R(x，y)=1－d(x，y)，其中 d(x，y)是U:P×A×D上欧氏归一化距离，则R是U:P×A×D上的一个模糊相似关系。

证明 R(x，x)=1－d(x，x)=1满足定义 16的条件(1);

R(x，y)=1－d(x，y)=1－d(y，x)=R(y，x)满足定义16的条件(2)。证毕。

定理5 设模糊矩阵A，则A的传递闭包t(A)是

证明略。

定理6 模糊相似矩阵R的传递闭包是模糊等价矩阵，且

证明略。

定理7 设R是模糊相似矩阵，则存在一个最小自然数 k(k≤n)，使得传递闭包 t(R)=于任何自然数 b≥k，都有 Rb=Rk，此时t(R)=是模糊等价矩阵［7］。

证明略。

定理 8 令 R(x，y)=1－d(x，y)，其中 d(x，y)是 U:P×A×D 上欧氏归一化距离，由 R(x，y)组成矩阵 R∈μ24×24，其中 μi×j=R(xi，yj)，则有模糊等价矩阵t(R)=，k(k≤n)。

证明:由定理4和定理7可证。

根据表1和定理4计算PAD情感空间论域U:P×A×D上的模糊相似关系矩阵。

根据定理8和式(7)求得R对应的模糊等价矩阵。

定义17 R是由式(8)确定的模糊等价关系，Rλ为R的截关系，Rλ构造的对应情感商空间为U(λ)={U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)}，则称 U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)为 Rλ的情感粒。

定义18 根据定义2和定义17，Rλ的情感粒度定义为

式中: A 表示A的基数。情感粒度是衡量PAD情感空间上的情感粒粗细度的尺度之一。

定理9 R是由式(8)确定的模糊等价关系，Rλ为R的截关系，且由Rλ构造的对应情感商空间为 U(λ)={U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)}，则有

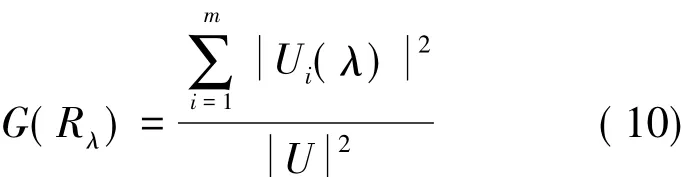
证明 由定理1同理可得。

定义19 R是由式(8)确定的模糊等价关系，Rλ为R的截关系，且由Rλ构造的对应情感商空间为 U(λ)={U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)}，则Rλ在U的子集构成的σ－代数上定义的概率分布为

定义20 R是由式(8)确定的模糊等价关系，Rλ为R的截关系，且由Rλ构造的对应情感商空间为 U(λ)={U1(λ)，U2(λ)，Ui(λ)，…，Um(λ)}，定义Rλ的PAD情感空间上的情感熵H(R)为

情感熵也是衡量PAD情感空间上的情感粒粗细度的尺度之一。

例1 对于式(8)的模糊等价矩阵，求取该模糊等价矩阵的截关系矩阵Rλ，λ=0．87时的情感商空间、情感粒度、情感熵。

解:

由式(8)和 Rλ，λ=0．87 可得

由定义15得R0．87等价截关系下的一个情感商集［U］:P×A×D 为:

{{钦佩，满足，感激，幸福，希望，高兴，喜欢，爱，傲慢，轻松，满意}，{发怒，厌恶，憎恨，责备}，{失望，痛苦，害怕，恐惧，同情，懊悔，愤恨，羞愧}，{幸灾乐祸}}

上式中:{钦佩，满足，感激，幸福，希望，高兴，喜欢，爱，傲慢，轻松，满意}是原情感空间U:P×A×D上比较正性情感的集合，{发怒，厌恶，憎恨，责备}是原情感空间U:P×A×D上比较负性且直接作用于客体的情感的集合，{失望，痛苦，害怕，恐惧，同情，懊悔，愤恨，羞愧}是原情感空间U:P×A×D上比较负性且比较倾向于内省的情感的集合，{幸灾乐祸}是原情感空间U:P×A×D上无利益冲突时表现出的负面情感的集合，该结果证明了通过R0．87等价截关系求得的商集，能够有效地将原空间提升到更宏观的层面进行描述和总结。

情感商空间的情感粒度

情感熵

例2 对于式(8)的模糊等价矩阵，分别取该模糊等价矩阵的截关系矩阵 Rλ1，λ1=0．87 和 Rλ2，λ2=0．9，试比较两者产生的情感商空间的情感粒粗细度。

解:

由式(8)和 Rλ，λ=0．9 可得

由定义15得R0．87等价关系下的一个情感商集［U］:P×A×D］为:

{{钦佩，满足，感激，幸福，希望，高兴，喜欢，爱，傲慢}，{发怒，憎恨}，{厌恶}，{失望，痛苦，恐惧，同情，懊悔，羞愧}，{害怕}，{幸灾乐祸}，{轻松，满意}，{责备}，{愤恨}}

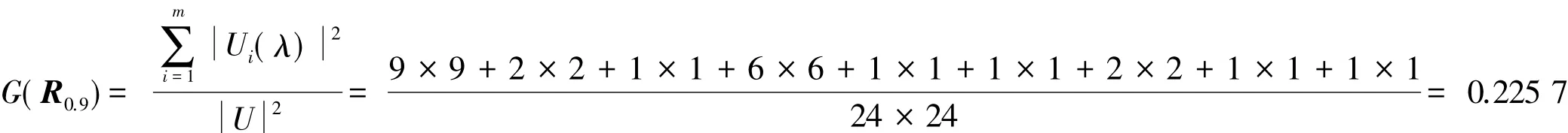
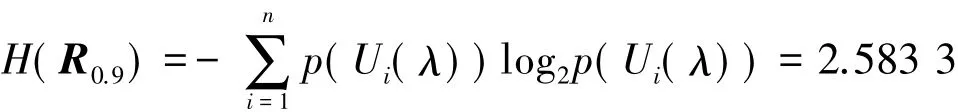
由定义 3、性质 2、性质 3 和 G(R0．87) ＞G(R0．9)、H(R0．87)＜H(R0．9) 可得 R0．87的情感商空间比 R0．9的情感商空间粗。

比较 R0．87的情感商空间和 R0．9的情感商空间，可以发现 R0．87的情感商空间是 R0．9的情感商空间集合的集合，也证明了R0．87的情感商空间是R0．9的情感商空间的商空间。

5 结 论

情感的可计算问题一直是人工智能领域研究的热点之一。情感计算的关键是将情感投影到特定空间上进行量化，并建立起有效的数学模型对其进行相关的计算，计算结果可以为后续的情感推理模型提供依据。本文以基于商空间理论的粒模型和粒计算为方法，对PAD情感模型进行了粒的描述。从粒的角度，定性和定量地刻画了PAD情感空间里的情感状态。通过实例证明了基于商空间理论的粒模型在描述PAD情感状态上具有一定的有效性和可行性。目前本文只是对PAD情感模型作了初步的粒描述。未来还将研究通过基于商空间理论的粒模型和粒计算的方法，定性和定量地描述情感在不同商空间上的拓扑关系以及情感在不同商空间上的运算法则，从而实现情感在不同层面(商空间)上的迁移、合成和分解等。

［1］ 张文修，吴伟志，梁吉业．粗糙集理论与方法［M］．北京:科学出版社，2001．ZHANG Wenxiu，WU Weizhi，LIANG Jiye．The rough set theory and method［M］．Beijing:Science Press，2001．

［2］ 苗夺谦，范世栋．知识的粒度计算及应用［J］．系统工程理论与实践，2002，22(1):48－56．MIAO Duoqian，FAN Shidong．The knowledge of granularity and its application［J］．Systems Engineering-Theory ＆ Practice，2002，22(1):48－56．

［3］ Duntsch I，Gediga G．Uncertainty measures of rough set prediction［J］．Artificial Intelligence，1998，106:109－137．

［4］ 苗夺谦，王国胤，刘清，等．粒计算:过去、现在与展望［M］．北京:科学出版社，2007．MIAO Duoqian，WANG Yinguo，LIU Qing，et al．Granular computing:history，currency and outlook［M］．Beijing:Science Press，2007．

［5］ 张玲，张钹．模糊商空间理论(模糊粒度计算方法)［J］．软件学报，2003，14(4):770－777．ZHANG Ling，ZHANG Bo．Theory of fuzzy quotient space(methods of fuzzy granular computing) ［J］．Journal of Software，2003，14(4):770－777．

［6］ Mehrabian A．Pleasure-Arousal-Dominance:A general framework for describing and measuring individual differences in temperament［J］．Current Psychology:Developmental，Learning，Personality，Social，1996，14(4):2612－2921．

［7］ 李柏年．模糊数学及其应用［M］．合肥:合肥工业大学出版社，2007．LI Bainian．Fuzzy mathematics and its application［M］．Hefei:Hefei University of Technology Press，2007．