动态非短视资产负债管理

张 玲, 张未未, 郑 军

(1.广东金融学院 经济贸易系,广东 广州 510521;2.惠州学院 数学系,广东 惠州 516007;3.广东财经大学 金融学院,广东 广州 510320)



动态非短视资产负债管理

张 玲1, 张未未2, 郑 军3

(1.广东金融学院 经济贸易系,广东 广州 510521;2.惠州学院 数学系,广东 惠州 516007;3.广东财经大学 金融学院,广东 广州 510320)

用均值-回复过程刻画股票价格变化，本文研究了股票收益可预测金融市场中的连续时间资产负债管理问题。运用动态规划方法，求得了最优资产负债管理策略的闭合解。结果表明，最优策略是风险溢价的线性函数，随着投资期限的缩短，股票上的投资金额不断降低。数值分析表明，投资期限、股票风险溢价和债务对于最优资产配置策略和股票风险溢价不确定性跨期对冲需求都存在显著影响。

资产负债管理;均值-回复过程;可预测性;HJB方程

0 引言

股票收益预测性是金融经济学研究的核心内容之一，投资组合管理、市场有效性和交易成本等问题的研究都必须考虑股票收益的预测性，研究发现历史收益率、盈余价格比、股息价格比、通货膨胀率等变量可用来预测股票的收益率。Campbell和Shiller[1]、Fama和French[2]的实证研究发现股票超额收益是时变、可预测的Ang和Bekaert[3]发现短期国库券的利率可以有效预测股票收益率，且这种预测能力在国际金融市场数据中的表现也是显著的。

近年，国内学者针对中国股票市场也开展了股票收益预测性的研究。姜富伟等[4]发现，各类成分投资组合的样本内和样本外预测都是显著的，且时变风险溢价有助于解释中国股票收益的预测性。秦泰和刘红忠[5]发现M1月环比增长率能够显著而稳定的预测股票超额收益率，且长期来看，根据M1月环比增长率构建的预测模型能够带来更高的投资绩效。

股票收益预测性已经成为国内外学术界的共识，针对股票收益预测性如何影响资产配置这一问题，大量学者进行了相关研究。Kim和Omberg[6]发现预测使得HARA效用下的资产配置策略敏感依赖于股票风险溢价。Barberis[7]指出股票收益预测导致投资者增加在股票上配置的资金。Xia[8]的研究表明预测的不确定性通过投资者动态学习行为影响资产配置，且诱导了最优策略与投资期限之间的状态相依。Watcher和Warusawitharana[9]发现即使是对股票收益预测性持高度怀疑态度的投资者，其基于股利率和期限利差预测做出的资产配置仍会收到较好的投资收益。Chen等[10]利用VAR模型刻画股票收益过程，研究了模型不确定情况下收益预测性对资产配置的影响，发现持怀疑态度的投资者会大幅降低其在股票上的投资。杨朝军等[11]基于中国股票市场的研究表明，长期投资者的资产配置策略与短期投资者的资产配置策略存在显著差异。综合已有研究我们发现，股票收益预测会导致资产配置策略与投资期限的状态相依，长期投资者配置在股票上的资金显著多于短期投资者，这与传统观点中认为的长期投资者应配置更多的资金到股票上是一致的。上述研究充分表明，在最优资产组合选择问题的研究和实践中，股票收益预测是投资者必须考虑的重要现实因素。

投资活动中，投资者不仅关注财富增长，还需要考虑投资过程中的债务。无论机构投资者还是个体投资者，债务都是投资者在资产管理过程中无法忽视的重要因素。随着资产规模的增大，债务导致的净资金流短缺风险会使得投资决策存在显著偏差，忽视债务将导致投资决策无法有效对冲风险。尤其是对于投资期限较长的养老金计划，跨期风险对冲需求显得尤为关键。资产负债管理，又称盈余管理，主要研究如何设计有效的风险管理策略。连续时间优化控制方法的发展，使得连续时间资产负债管理策略的求解成为可能，近年涌现了大量的研究成果。Rudolf和Ziemba[12]用几何布朗运动描述状态变量的动态过程，研究了终端盈余效用最大化问题。Van Binsbergen和Brandt[13]利用Gaussian VAR过程模拟状态变量的动态过程，发现最优组合策略独立于资金比率。Chiu和Li[14]考虑了均值-方差效用下的连续时间资产负债管理问题，利用随机LQ方法和嵌入法得到了最优资产负债管理策略和最优初始资金比率。 Detemple和Rindisbacher[15]考虑了投资者偏好依赖资金比率时最低债务偿付对最优资产负债管理策略的影响。Ferstl和Weissensteiner[16]采用情景生成方法研究了投资机会集合时变的动态资产负债管理。Wei等[17]考虑了均值-方差资产负债管理问题的时间一致性策略。

上述资产负债管理问题的研究中，股票价格的运动过程通常用几何布朗运动刻画，且模型参数通常设定为定常的，即股票收益是独立同分布的、股票的即时收益率和波动率是确定的常数，这与金融市场中股票价格的表现有较大的距离。事实上，资产管理过程中，投资者通常利用已有信息来预测股票的收益率，做出资产管理决策。基于此，本文突破股票即时收益率是常数的设定，假定股票即时收益率是时变的，且服从O-U过程；在股票收益可预测的金融市场中，利用带漂移的布朗运动刻画债务的动态演变过程，求解HJB方程得到了最优资产负债管理策略的闭合解。结果表明，最优资产负债管理策略是非短视的，且是风险溢价的线性函数。在校准模型参数的基础上，给出了风险溢价、投资期限和债务对最优资产负债管理策略以及风险溢价不确定性对冲需求影响的数值分析。

1 模型

投资者在时刻0以净资产w0进入金融市场，计划进行时间长度为T的投资活动。在整个投资期[0,T]内，投资者可以连续调整其在无风险资产和股票上的头寸而不需要支付交易费用。投资期[0,T]内，不考虑消费和随机收入。

1.1 金融市场

假定在整个投资期[0,T]内，无风险资产的利率是常数r，r>0，且价格过程B={Bt,0≤t≤T}满足

dBt=rBtdt

(1)

在分红再投资的情形下，股票价格过程S={St,0≤t≤T}满足下面的随机微分方程

(2)

(3)

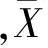
投资过程中，投资者需要抽出部分资金以偿还债务。令Lt表示时刻t累积外生负债，其动态变化过程L={Lt,0≤t≤T}满足

(4)

其中ν表示债务的即时收益率。σL>0代表债务的波动率，zL是均值为0方差为1的一维标准布朗运动，E[dzdzL]=ρSLdt。

1.2 资产负债管理问题

令αt表示时刻t投资在股票上的资金数额，则α={αt,0≤t≤T}是整个投资周期内的资产配置策略。令Wt表示时刻t在策略α下投资者的净资产，那么时刻配置在无风险资产上的资金数额为Wt-αt，因此投资者财富过程W={Wt,0≤t≤T}满足

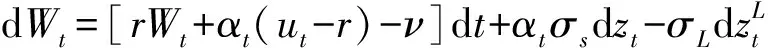
(5)

投资者希望寻找到最优资产负债管理策略α，使得在时刻T投资结束时其终端净资产WT的效用最大化，即投资者期望解决以下优化问题：

(6)

其中，γ>1代表投资者的风险厌恶程度。

2 最优资产负债管理策略

令

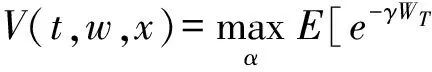
表示在时刻t问题(6)从状态Wt=w、Xt=x出发的最优值函数，则最优值函数V(t,w,x)满足下面的Hamilton-Jacobi-Bellman(HJB)方程

(7)

边界条件为V(T,w,x)=e-γw。下面的命题，给出了HJB方程(7)的最优解和最优资产负债管理策略。

命题1 HJB方程(7)的最优解为

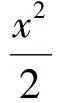
(8)

相应的最优资产负债管理策略为

(9)

其中τ=T-t，

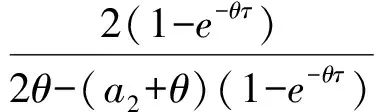
(10)

(11)

(12)

证明 考虑HJB方程(7)诸如

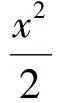
对V(t,w,x)关于t,w,x求一阶、二阶偏导数，有

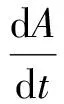
(13)

将上述V(t,w,x)对t,w,x的一阶、二阶偏导数代入HJB方程(7)得到

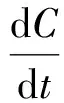
(14)

(15)

(16)

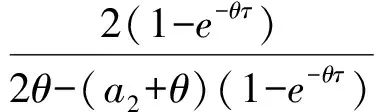
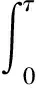
将B(τ),C(τ)代入方程(16)，且方程两边求积分得到方程(16)的解为

证毕。

3 最优资产负债管理策略灵敏性分析

本节将分析股票风险溢价、投资期限和负债对资产负债管理策略的影响，考虑投资期限T分别为6个月(6M)、1年(1Y)、5年(5Y)、10年(10Y)和30年(30Y)、投资者初始净资产为1的情况。

3.1 参数校准

依据Barberis[7]和Wachter[17]的计算方法，校准模型参数，如表1所示。

表1 数值分析中所需参数值，所有参数以月为单位

3.2 风险溢价对资产负债管理策略的影响

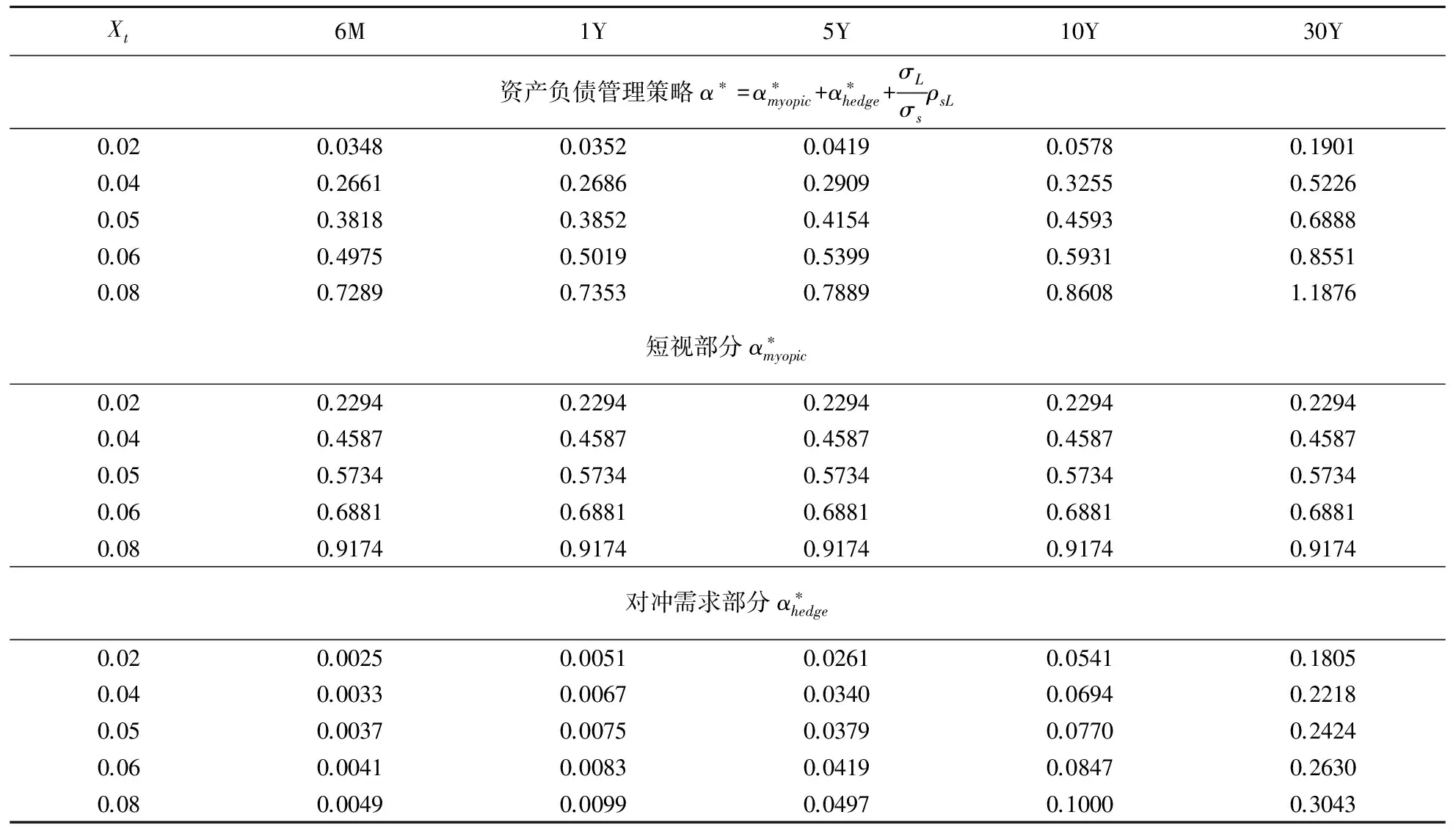
表2 风险厌恶因子γ=5时，不同投资期限和风险溢价下的资产负债管理策略、短视策略和对冲需求

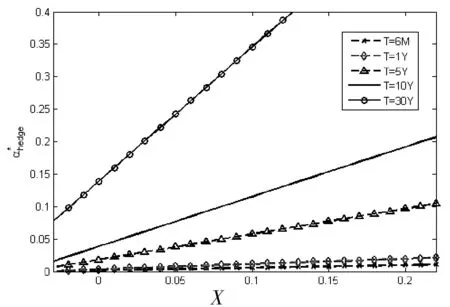
图1 γ=5时风险溢价不确定性对冲需求与风险溢价X的关系

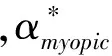
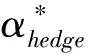
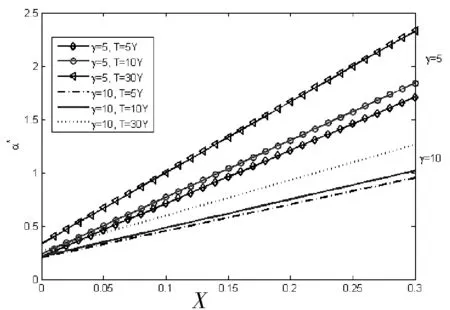
图2 风险厌恶因子为5和10，投资期限为5Y、10Y和30Y时风险溢价与资产负债管理策略的关系

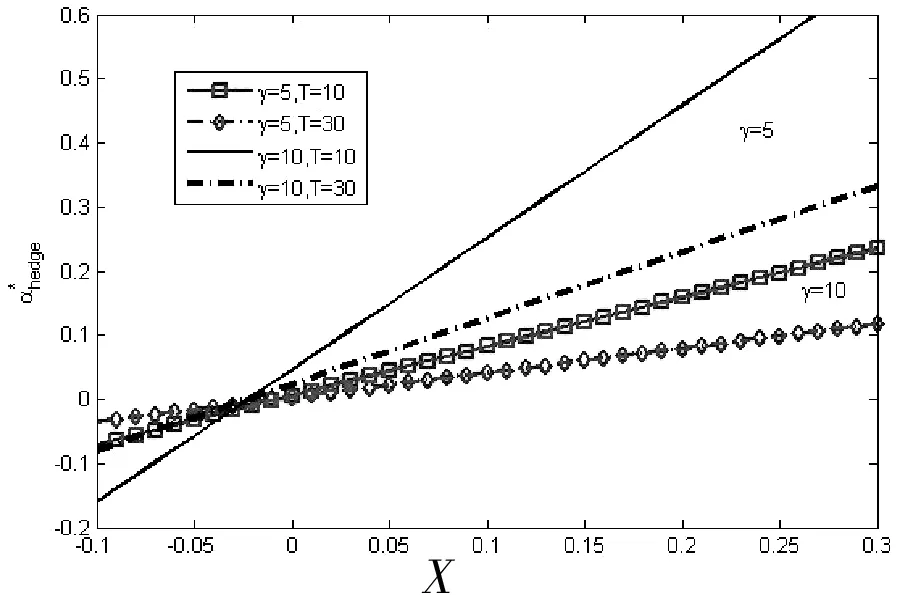
图3 风险厌恶因子为5和10，投资期限为10Y和30Y时风险溢价与对冲需求的关系

图2对比了不同风险厌恶程度下风险溢价与最优策略的关系，图3表示风险溢价与对冲需求之间的关系。在相同的风险溢价X下，风险厌恶因子越低，配置在股票上的资金越多，跨期风险对冲需求越高。尽管存在小部分区域使得X<0时对冲需求是正的，但总体来看，风险溢价X<0时，对冲需求为负；风险溢价X>0时，对冲需求为正。

图4 风险厌恶因子γ=5时资产负债管理策略与投资期限τ=T-t的关系

3.3 债务对资产负债管理策略的影响

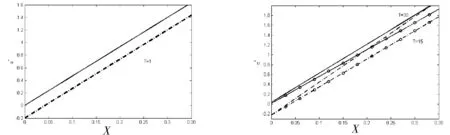
图5 T=1Y时，风险溢价与最优策略α*的关系 图6 T=15Y和T=30Y时，风险溢价与最优策略α*的关系

图5～图8中实线代表的考虑债务时的状况，虚线代表不考虑债务时的状况。图5中，投资期限为1年时(T=1Y)，风险溢价X未显著影响股票上配置资金增加的幅度；而图6中投资期限为15年(T=15Y)和30年(T=30Y)时，风险溢价越大，考虑负债时配置到股票上资金增加的幅度小于未考虑负债时增加的幅度。也就是说债务的引入使得配置到股票上的资金增加，但是随着投资期限的拉长，有负债时股票上投资增加的幅度小于未考虑负债时增加的幅度。图7表明投资在股票上的资金随着投资期限的拉长而增大，且考虑债务时投资在股票上的资金增大的幅度远大于未考虑负债的情形。 图8表明，投资期限的拉长会加大非短视投资者对股票风险溢价不确定性的对冲需求，考虑负债时风险溢价不确定性的对冲需求大于未考虑负债的情形。

4 结论

本文利用均值-回复过程描述股票收益的动态变化、带漂移的布朗运动描述负债的动态过程，研究了资产收益可预测时的连续时间资产负债管理问题，求得了资产负债管理策略的最优闭合解。股票收益预测性导致最优资产负债管理策略由短视部分和股票风险溢价不确定性对冲需求两部分组成，是非短视的；最优资产负债管理策略是风险溢价的线性函数，且依赖于投资期限，接近于投资结束时，股票上配置的资金下降。数值分析表明，在资产收益可预测的金融市场中，考虑债务的长期投资者配置在股票上的资金多于短期投资者。由于非短视投资者会考虑到股票未来的风险溢价，风险溢价在不同水平上影响配置在股票上的资产。负债的引入导致股票风险溢价的对冲需求显著增大，但是随着风险溢价水平的提高，对冲需求增大的幅度降低。

[1] Campbell J Y, Shiller R J. The dividend price ratio and expectations of future dividends and discount factors[J]. The Review of Financial Studies, 1988 , 1: 195-228.

[2] Fama E F, French K. Dividend yields 和 expected stock returns[J]. Journal of Financial Economics, 1988, 22:3-27.

[3] Ang A, Bekaert G. Stock return predictability: Is it there? [J]. The Review of Financial Studies, 2007, 20: 651-707.

[4] 姜富伟, 涂俊, Rapach D E, Strauss J K, 周国富. 中国股票市场可预测性的实证研究 [J].金融研究,2011,9:107-121.

[5] 秦泰, 刘红忠. 超额收益的可预测性与资产配置——于中国股票市场数据的研究[J].复旦学报(社会科学版),2013, 6:107-119.

[6] Kim T S, Omber E. Dynamic nonmyopic portfolio behavior[J]. The Review of Financial Studies, 1996, 9(1): 141-161.

[7] Barberis N. Investing for the long run when returns are predictable[J]. Journal of Finance, 2000, 55: 225-264.

[8] Xia Y H. Learning about predictability: te effects of parameter uncertainty on dynamic asset allocation [J]. Journal of Finance, 2001, 56(1): 205-246.

[9] Wachter J A, Warusawitharana, M. Predictable returns and asset allocation: Should a skeptical investor time the market?[J] Journal of Econometrics, 2009, 148: 162-178.

[10] Chen H, Ju, N J, Miao J J. Dynamic asset allocation with ambiguous return predictability[J].The Review of Economic Dynamics, 2013. http://dx. doi.org/10.1016/j.red.2013.12.001.

[11] 杨朝军,陈浩武,杨玮沁.长期投资者收益可预测条件下的战略资产配置决策——理论与中国实证[J].中国管理科学, 2012, 20(3): 63- 69.

[12] Rudolf M, Ziemba W T. Intertemporal surplus management[J]. Journal of Economic Dynamics 和 Control, 2004, 28: 975-990.

[13] Van Binsbergen J H, Brandt M W. Optimal asset allocation in asset and liability management[J]. Working paper, Fuqua School of Management, Duke University, 2006.

[14] Chiu M C, Li D. Asset and liability management under a continuous-time mean-variance optimization framework[J]. Insurance: Mathematics and Economics, 2006, 39: 330-355.

[15] Detemple J, Rindisbacher M. Dynamic asset liability management with tolerance for limited shortfalls[J]. Insurance: Mathematics and Economics, 2008, 43: 281-294.

[16] Ferstl R, Weissensteiner A. Asset-liability management under time-varying investment opportunities[J]. Journal of Banking and Finance, 2011, 35: 182-192.

[17] Watchter J A. Optimal consumption and portfolio allocation under mean- reverting returns: an exact solution for complete }[J]. Journal of Financial and Quantitative Analysis, 2002, 37: 63-91.

Dynamic Nonmyopic Asset Liability Management

ZHANG Ling1, ZHANG Wei-wei2, ZHENG Jun3

(1.DepartmentofEconomicsandTrade,GuangzhouUniversityofFinance,Guangzhou510521,China; 2.DepartmentofMathematics,HuizhouUniversity,Huizhou516007,China; 3.SchoolofFinance,GuangdongUniversityofFinanceandEconomics,Guangzhou510320,China)

This paper investigates a continuous-time asset liability management problem by assuming that the stock returns are predictable which breaks the impasse that the returns of stock are independent identical distribution. The appreciation rate of the stock price is modulated by a mean-reverting process. And the dynamics of liability is described by a Brownian motion with drift. Utilizing the dynamic programming approach, this paper solves, in closed form, the optimal asset liability management strategy for an investor under expected utility over the terminal surplus. The result shows that the optimal asset liability management strategy is a linear function of risk premium and the amount invested in the risky stock decreases with the investment time horizon. The numerical analysis shows that the investment time horizon, risk premium and liability have significant impact on the optimal asset liability management strategy and the demand for hedging the uncertainty of the risk premium.

asset liability management; mean-reverting process; predictability; HJB equation

2014- 06- 12

教育部人文社会科学基金资助项目(13YJCZH247)；广东省哲学社会科学基金资助项目(GD12XYJ06)；广东金融学院“创新强校”工程资助项目“随机市场环境下的动态资产配置问题研究”。

张玲(1979-)女，副教授，理学博士，研究方向：投资组合与风险管理、金融经济学；张未未(1978-)，女，讲师，研究方向：最优资产组合选择；郑军(1982-)，男，博士，讲师，研究方向：金融经济学与经济机制理论。

F830

A

1007-3221(2015)06- 0225- 08

10.12005/orms.2015.0217