基于网络等级特征与VMS的交叉巢式Logit模型
曾明华, 云美萍, 杨晓光
(1.华东交通大学 轨道交通学院,江西 南昌 330013; 2.同济大学 交通运输工程学院,上海 201804)
基于网络等级特征与VMS的交叉巢式Logit模型
曾明华1, 云美萍2, 杨晓光2
(1.华东交通大学 轨道交通学院,江西 南昌 330013; 2.同济大学 交通运输工程学院,上海 201804)
基于等级特征与可变信息板(VMS)研究了交叉巢式Logit(CNL)模型及网络交通流分配。综合幂函数与指数函数表示方法给出新的信息效用衰减因子,结合道路等级特征表示VMS对车流的影响系数及CNL模型的分配系数;给出等级结构道路网络的随机用户均衡条件下的交叉巢式Logit路径选择模型及其等价数学规划,并设计网络流分配算法。通过实例网络的计算与分析,得到一些有意义的结论:等级结构越显著的路网总出行时间费用越低且其分散参数(θ)弹性绝对值越大;对具有较强随机性的实际路网,若增加一定的确定性则节省更多网络总出行时间;道路网络中设置了VMS时总出行时间受分散参数的影响更小。
交通运输规划与管理;交叉巢式Logit;随机用户均衡;等级性道路网络;路径选择行为;可变信息板
0 引言
等级特征是城市道路网络的普遍现象和典型特性,信息技术是重要城市交通管理工具。二者在现在城市交通系统中扮演重要角色,但少有成果刻画它们共同对交通系统性能所产生的影响。对该现实问题展开研究,揭示其中规律,为交通运输系统规划与管理提供借鉴。
出行者路径选择模型,对刻画出行行为尤其是路径选择行为至关重要,对交通网络流量加载会产生深刻影响。最常用的是基于随机效用模型的Logit路径选择模型,具有封闭的解析函数形式。对路径之间效用进行确定性的相关性校正的多项式Logit(MNL)模型和通过误差项分布假设和离散选择模型来进行相关性建模的交叉巢式(CNL)模型,是Logit模型的两类典型代表,它们各有长短,MNL模型简单却不能捕获路径的相关性结构,CNL模型正好相反。MNL模型应用非常广泛,而CNL模型在文献[1]中被应用于路径选择问题,文献[2]利用CNL模型研究多用户多模式随机用户均衡。考虑到CNL模型具有双层巢式结构,下层每条路径分配给上层所有构成该路径的路段,它们之间的分配系数是CNL模型的重要结构性参数,已有研究中主要利用路段距离等网络拓扑计算该参数[3]。
等级性是重要的路网特征,与路径选择行为存在密切联系。不少学者研究了等级级配[4]和等级划分[5];尽管在网络交通流分配中的应用研究不多,但工程实践与已有成果表明等级结构在优化路网性能方面具有显著作用[6,7]。可变信息板(VMS)在城市交通管理中的广泛经年使用中,对路径选择行为和路网交通流分布产生了不可忽视的影响。较多研究侧重于借助调查与统计以标定各种形式的VMS信息对不同性能评价指标或个体属性[8]共同表示的效用函数的影响,从而计算是否改变路径的概率;如何确定VMS位置以发挥最大效用并提高网络性能[9],也激发了不少学者的研究热情。
物理距离或路段旅行时间等传统物理量在反映信息作用时的局限性,而且,根据人类思维特点及消费者行为心理学可知出行者倾向于选择等级更高、信息服务更优的路段出行;但是,传统路径选择模型难以体现等级特征和信息融合现象,因此,利用新的方式计算CNL模型的分配参数以反应VMS信息技术的影响,研究路网中基于CNL模型的网络交通流分配。通过实例研究表明,所设计的交叉巢式Logit路径选择模型能够有效地反映路网的等级特征和VMS信息作用,并分析了等级特征与VMS信息影响下路网总时间费用关于CNL模型分散参数θ和嵌套参数μ的变化情况。
1 基于VMS和等级特征的CNL模型
1.1 基本符号
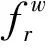
1.2 等级路网的CNL模型
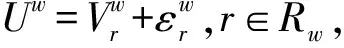
(1)
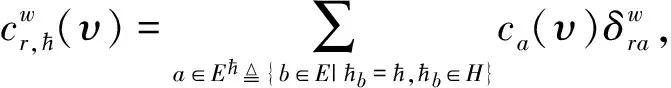
(2)
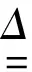
等级路网中OD对w间路径r的选择概率如下
(3)
其中:M是构成路径r的路段集合;αmr是刻画选择枝r分配到巢m的分配参数,αmr须满足αmr≥0且(∀r)∑mαmr=1;μm∈(0,1]是巢m的相异度参数,刻画了每个巢或簇团中选择枝效用的随机项之间的相似度或相关度;参数μ表示嵌套的程度。
1.3VMS影响指数与分配参数
(1)信息效用的衰减因子
信息效用随车辆获取信息时所处路段与VMS装设路段的距离增加而减弱,在VMS信息效用最大化研究文献中考虑了该特征,并用效用衰减因子来刻画[9, 11],下面简单介绍并设计新的衰减因子。
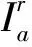
(4)
(2)VMS信息的影响系数
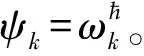
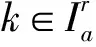
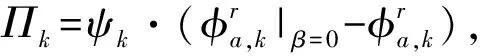
(5)
而VMS下游没有受到影响的路段则为
(6)
其中:za表示是否设置VMS的0-1变量。故将路段a上所设置VMS对路径r上车流的影响系数表示为
Πa=za∑Πk,∀a|za=1
(7)
该式表明,路段a的后续路段等级越低,影响系数越大,VMS的效用越大;β越大,衰减因子越小,VMS的效用越大。
(3)计算分配参数
CNL模型(3)包括了大量的结构参数,一些文献利用网络拓扑计算分配参数[3]以降低问题复杂性,结合本节(1)与(2)的研究,定义分配参数如下
αar=(La/Lr)γδra,∀a∈E,r∈Rw
La=arctan(ca)·exp(-Πa),∀a∈E
(8)
Lr=∑a∈MLa
其中:γ反映出行者对路径之间相似性的感知,为γ是待校正参数,为方便起见令γ=1[3];Λmr是路段-路径关联系数(0-1数);路段a在路径r中的分配系数αar与路段等级、路段长度、及其VMS影响系数有关,取γ=1则∑aαar=1。需要说明的是,当没有设置VMS时,令La=ca。
2 CNL-SUE模型及路网流量分配算法
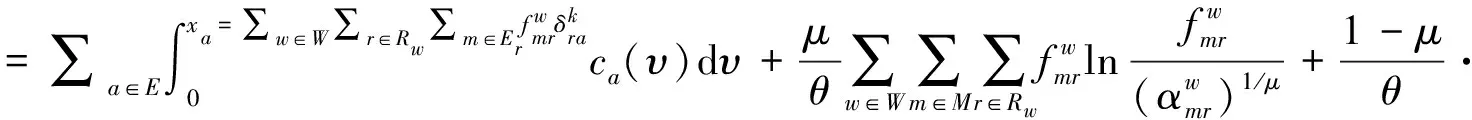
(9)
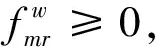
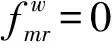
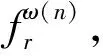
(10)
路网流量分配算法步骤:
Step 0 初始化。读入路段容量、OD流量等已知量;给定参数值;给定初始可行解f(0);置n←0。
Step 1 下降方向。更新费用c(n)=c(f(n)),计算分配参数,求解部分线性化子问题(10)得到辅助流量h(n);若d(n)=h(n)-f(n)≠0,则定义目标函数(9)的一个下降方向为d(n)=h(n)-f(n)。
Step 3 流量更新。f(n+1)=f(n)+ss(n)·(h(n)-f(n))。
Step 4 终止条件。若满足终止条件(11):
(11)
则退出;否则,置n←n+1,转Step 1。
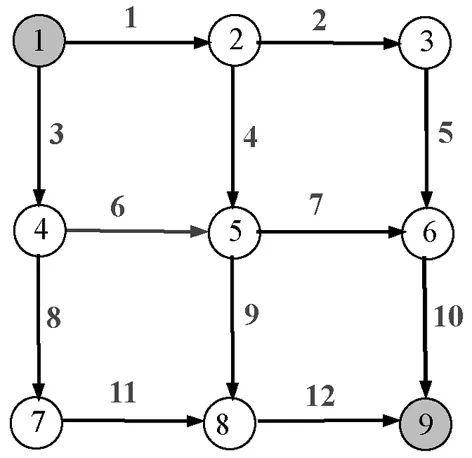
图1 实例网络
3 实例分析
采用9个节点的实例网络图1,路段旁边的数字表示路段标号。OD对1→9的流量为q19=600veh。不失一般性,假设在路段4、7上安装有VMS装置;假设路网共有两个等级,路段4、6、7、9是较高等级ћ1,其他为较低等级ћ2,相应的层次因子为Iћ,ћ∈H={ћ1,ћ2}。用Rl0代表无等级特征的路网结构,Rlx,x∈{1,2…,5}分别表示各种等级结构路网中较高等级与较低等级的层次因子数值比率(HFR),即Rl1=0.6/0.4=1.5、Rl2=0.612/0.388=1.576、Rl3=0.625/0.375=1.67、Rl4=0.634/0.366=1.73、Rl5=0.667/0.333=2。

表1 已知参数
设置参数:ε=0.001,θ=1,μ=0.34,γ=1.0,δ=2,β=1;若无特殊说明,这些参数值不变。其中,δ的取值依据网络大小而定;对β而言,取其他值并不影响研究结果,且其他参数一定的情况下,设置了VMS时信息衰减函数的常数因子β越大,网络总时间费用越低。
(1)路网总时间费用
路网总时间费用(NTTC)按下式计算
NTTC=∑a∈Eca(v)va
(12)
令μ=0.01,0.1,0.34,0.85,1.0,对Rl0,Rl1,Rl2,Rl3,Rl4,Rl5,分别在设置了VMS和没有设置VMS情况下计算。对于分配参数没有考虑VMS的情况(记为NVMS)而言,如图2(a)所示,可得出如下结论:(1)不论是MNL、还是CNL,在给定一个μ值的情况下,等级特征越明显,网络的总时间费用越低;(2)对任何等级结构路网,网络总时间费用相对于μ呈下降趋势,且利用MNL模型计算得到的网络总时间费用低于CNL模型;(3)对于分配参数中考虑VMS的情况而言,也有相同结论,如图2(b)所示。
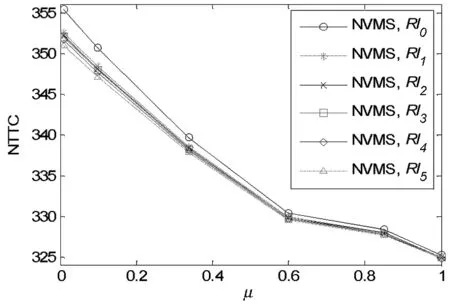
图2(a) 无VMS信息情形下的NTTC-μ关系图
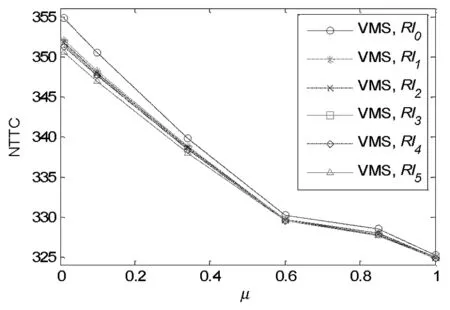
图2(b) 有VMS信息情形下的NTTC-μ关系图
(2)网络总时间费用的θ弹性
定义参数θ对网络总时间费用的影响为网络总时间费用θ弹性(NTTCTE)
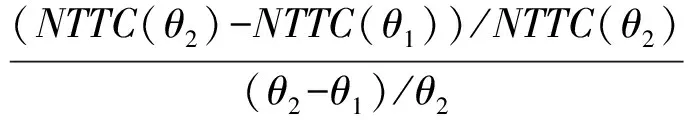
(13)
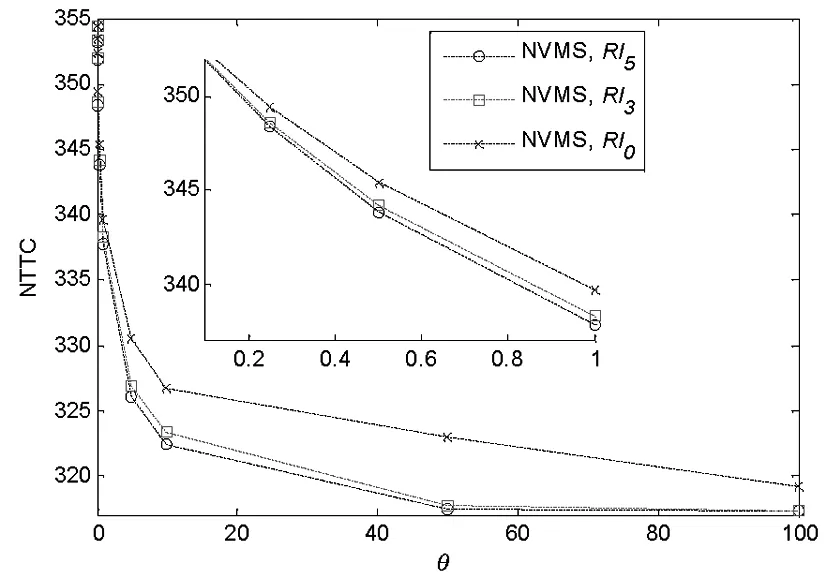
图3(a) 无VMS信息情形下的NTTC-θ关系图
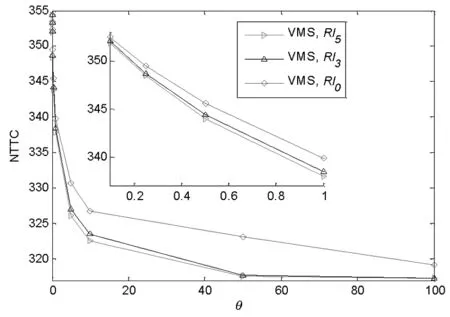
图3(b) 有VMS信息情形下的NTTC-θ关系图
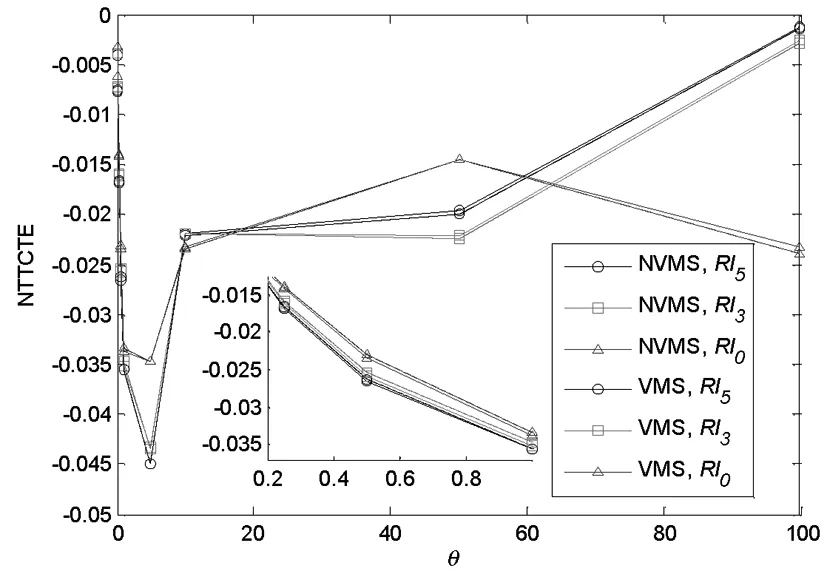
图4 网络总时间费用的θ弹性
没有设置和设置了VMS情况下,计算了网络总时间费用θ弹性。两种情况下的网络总时间费用θ弹性见图4 所示:当θ较小时,如θ∈(0,1),不管是没有设置VMS还是设置了VMS,等级特征强的网络的总时间费用的θ弹性绝对值比等级特征弱的大,这表明等级特征越明显θ增大所带来的网络总时间费用节省越多;对特定网络结构而言,有VMS信息的网络总时间费用的θ弹性绝对值比没有VMS信息时小,这说明在有VMS信息情况下θ的变化对网络总时间费用影响更小。当θ取更大值时,会出现波动;当θ取值很大,如大于80后,网络趋于非常确定,此时网络总时间费用θ弹性正好与较小θ时相反。
因此,结合(1)与(2)的分析,得出如下结论:对网络特定随机程度或CNL模型的特定嵌套程度,网络等级能够优化以网络总时间为准则的路网性能;因现实路网随机性较强,故更显著的等级特征能因θ在局域内增大而节省网络总时间;网络中设置VMS信息时总时间受θ影响更小。
(3)CNL模型与MNL模型之间路径流量解差别
在(1)的计算结果中,已经表明MNL模型的网络总时间费用比任何嵌套结构的CNL模型都小。在此,将基于收敛路径流量定义了如下准则以比较CNL模型与MNL模型两种分配方式之间的差异。
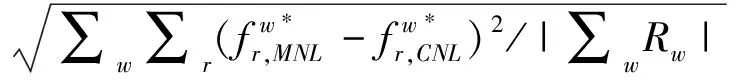
(14)
计算RMSE2,得到图5(a)与(b)所示结果。可知:对任何等级结构网络,无论其中是否设置了VMS装置,RMSE2随μ值增大而减小;在没有设置VMS装置的无等级特征路网中,CNL模型与MNL模型之间差别最明显,等级特征越明显的路网中这种差别越小;有VMS信息时,可得出类似的结论。
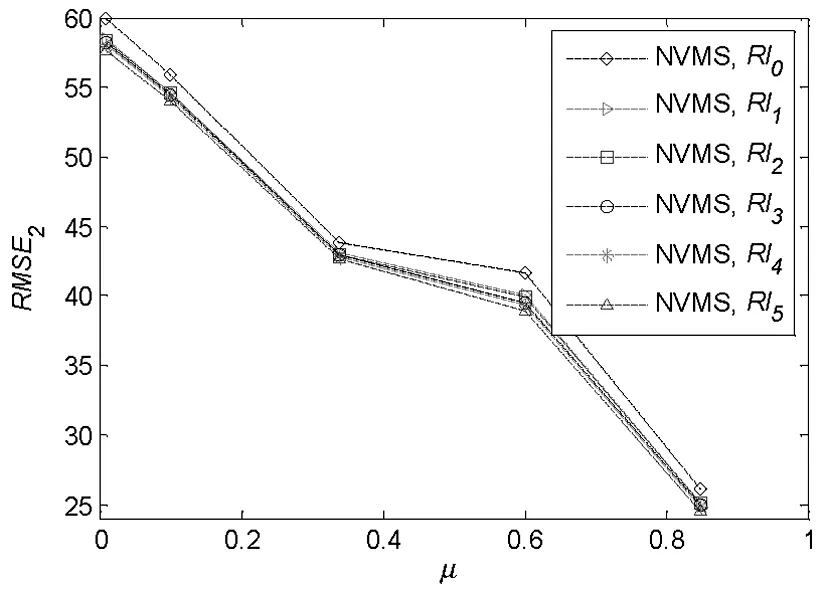
图5(a) 无VMS信息时的RMSE2-μ关系图
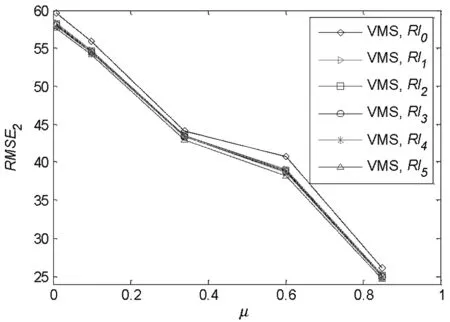
图5(b) 有VMS信息时的RMSE2-μ关系图
(4)调整图1的网络结构并计算分析
在图1 中,改变网络拓扑结构,新建路段(1,5)和(5,9),各自的FFTT(h)分别为3.5和2.5,各自的容量(veh)都为280。并调整网络的等级结构,假设分为2个层次:路段(1,5)、(4,5)、(5,6)、(5,9)是较高层次路段,其他为较低层次路段,VMS的设置与图1 一致。在所有参数和计算方式一样的情况下,通过对所有计算结果的详细比较与分析,得到了与上述(1)、(2)、(3)完全一致的结论。
4 结论
道路网络等级结构是功能结构的支撑,等级结构影响布局结构形态和居民出行需求分布。等级特性在城市路网规划的工程实践中得到了广泛的应用,且当今先进信息在道路网络中使用越来越广,因此,在设置了VMS信息的等级性道路网络中研究出行者的路径选择行为和交通需求在路网的分配。基于等级特征的和VMS信息效用衰减因子,建立随机用户均衡的交叉巢式Logit路径选择模型和等价数学规划模型,并设计相应的网络交通流加载算法。研究得到有价值的结论: (1)更接近实际路网随机性较强的情况(分散参数取较小值时),等级特征可以提高以网络总时间费用为指标的道路网络性能,VMS信息能缓冲分散参数变化对路网性能的影响;而路网确定性较强的情况(分散参数取较大值时,这与现实有异),情形相反。 (2)基于MNL模型的随机用户均衡交通流加载所得路网总时间费用低于任何嵌套参数下的CNL模型,且嵌套参数越大CNL模型与MNL差异越小。
研究结论表明了等级特征与VMS信息在何种情况下能优化道路网络性能;进一步可研究混合交通流和交通拥堵的情形下如何优化等级路网的性能。
[1] Prashker J N, Bekhor S. Investigation of stochastic network loading procedures[J]. Transportation Research Record: Journal of the Transportation Research Board, 1998, 1645(1): 94-102.
[2] 胡文君,周溪召.基于交叉巢式Logit的多用户多模式随机用户均衡模型[J].中国公路学报,2012,25(4):133-140.
[3] Bekhor S, Ben-Akiva M E, Ramming M S. Evaluation of choice set generation algorithms for route choice models[J]. Annals Of Operations Research, 2006, 144(1): 235-247.
[4] 石飞.城市道路等级级配及布局方法研究[D].南京:东南大学博士学位论文,2006.
[5] 叶彭姚,陈小鸿.基于道路骨架性的城市道路等级划分方法[J].同济大学学报(自然科学版),2011,39(6):853- 856.
[6] 曾明华,李夏苗.多层次多模式综合交通网络设计研究[J].交通运输系统工程与信息,2010,10(2):23-29.
[7] 曾明华,李夏苗.基于层次性的交通网络资源优化配置方法[J].中南大学学报(自然科学版),2011,42(1):247-253.
[8] 徐天东,孙立军,媛郝,等.不同交通信息下网络交通动态路径选择行为[J].同济大学学报(自然科学版),2009,37(6):1029-1034.
[9] 杨远舟,毛保华,张笑杰,等.基于路径诱导的高负荷路网微循环组织研究[J].系统仿真学报,2010,22(7):1580-1584.
[10] McFadden D. Modelling the choice of residential location[J]. Transportation Research Record, 1978, 672: 72-77.
[11] 倪富健,刘志超.可变交通信息牌的最优分布模型[J].信息与控制,2003,32(5):395-398.
A Modified Cross Nested Logit Route Choice Model Based on Network Hierarchy and VMS Information
ZENG Ming-hua1, YUN Mei-ping2, YANG Xiao-guang2
(1.SchoolofRailwayTracksandTransportation,EastChinaJiaoTongUniversity,Nanchang330013,China; 2.SchoolofTransportationEngineering,TongjiUniversity,Shanghai201804,China)
Network traffic assignment and cross-nested Logit(CNL)model are investigated based on road hierarchy and VMS information. Supposing some main roads are installed with VMS equipment, the impact coefficients on traffic flow by VMS and the allocation coefficients in CNL model are calculated with road grade and a new attenuation factor of information utility that is formulated by integrating power and exponential ones. For hierarchical road network, CNL route choice model and its equivalent mathematical programming are established under the stochastic user equilibrium, and then a network flow allocation algorithm is proposed. The model and algorithm presented are examined with an example network. Calculations and analyses lead to some meaningful conclusions. The more significant hierarchical structure of road network, the lower the total travel time and the greater the absolute value of its elasticity on the diffusion parameter(θ). The enhancement of determinacy of the real road network that has relatively strong randomness will save more travel time. The road network installed with VMS is more slightly affected by dispersion parameter when the performance is measured by total travel time.
Transportation planning and management; cross-nested Logit; stochastic user equilibrium; hierarchical road network; route choice behavior; VMS
2014- 03-28
国家自然科学基金项目(51468020);中国博士后基金(2014M561519);江西省科技支撑计划(20151BBG70056);江西省自然科学基金资助项目(C20141BAB207016)
曾明华(1977-),男,博士,副教授,研究方向:交通系统建模、智能交通系统工程;云美萍(1977-),女,博士,副教授,博士生导师,研究方向:智能交通系统、交通行为分析;杨晓光(1959-),男,博士,教授,博士生导师,研究方向:交通运输规划与管理、智能交通。
U491;O22
A
1007-3221(2015)06- 0199- 06
10.12005/orms.2015.0213

