施工项目中设计风险元传递模型研究

李存斌， 刘赟奇， 李书科

(华北电力大学 经济与管理学院，北京 102206)



施工项目中设计风险元传递模型研究

李存斌， 刘赟奇， 李书科

(华北电力大学 经济与管理学院，北京 102206)

针对设计变更对项目实施的影响，本文将影响施工项目的设计变更原因称为项目的设计风险元，基于广义项目风险元传递理论建立系统动力学模型，动态研究设计风险元传递过程。通过模型模拟分析不同时间、不同程度的设计风险元对项目工期和项目费用影响程度，当设计风险元发生后，设计审批及设计过程将影响项目工期；受施工工序影响设计风险元造成实际施工速度不饱和，使得施工效率低下形成窝工；由于设计风险元导致的返工造成施工项目的工期延误和成本超支。此模型为风险管理者或项目管理者在设计风险管理方面提供了有力依据。

项目管理；设计风险；风险元传递；系统动力学

0 引言

设计风险是在施工过程中导致返工的主要原因之一，这往往会迫使项目管理者延长项目工期或增加项目费用支出[1,2]；无论一个人的技能水平有多高、经验有多足，受人类的生理和心理的限制，设计风险可能发生在任何时间里[3]。在实践中，设计和施工组织只是通过有限的精力和注意力去关注这些风险，并不能有效地预测和规避，从而导致了项目施工过程中需要返工[4,5]。

项目风险应对是风险管理的一个值得关注的重要研究问题[6],随着工程项目建设规模的扩大、建设周期的延长以及项目环境的日趋复杂，项目设计风险也随之不断复杂化，国外文献[7～10]分别从不同角度和方面对设计风险进行了研究；国内学者也对设计风险进行较多的研究[11～14]。然而，项目的一个风险元的微小变化，经过连锁反应影响，可能会导致企业目标的巨大偏离[15]。因此，项目风险管理有必要研究风险的传递影响，即项目风险元传递[16]。在本文，将导致工程量变化的各种设计变更原因称为项目的设计风险元。

关于对风险的界定，学者们有不同的观点[17]，本文作者已在项目风险元传递方面做过研究：将项目的基础风险变量定义为风险元，并提出了不同的风险元度量方法；研究了经济评价项目中风险元传递对项目投资的影响；利用数据挖掘技术建立工程项目风险元传递矩阵，以此为基础判断和比较不同风险元的传递影响；基于风险元传递理论研究了多目标工程项目中风险、工期与费用三者之间的均衡问题；针对项目风险，提出了基于GERT网络计划的风险元传递解析模型，以此来研究项目工期风险元传递影响。而本文将运用系统动力学来研究施工项目中的设计风险元传递问题。

系统动力学(System dynamics, SD)的概念和理论最初由Forrester教授提出[18]，并得到广泛应用，其最突出的特点是能够处理非线性高阶层多重反馈复杂时变的系统问题[19]。Wang等[20]专门论证了系统动力学在项目风险管理中的优势；文献[21]运用系统动力学定量地研究风险元是如何通过工程项目系统内部结构在项目进行过程中动态影响项目目标。本文首先分析设计风险元的传递过程，给出系统框架，接着运用Vensim软件对系统中的各组成要素和要素间的关系进行剖析，最终形成整体循环体系，对模拟结果进行对比分析并给出结论。

1 设计风险元传递系统分析

1.1 设计风险元分析

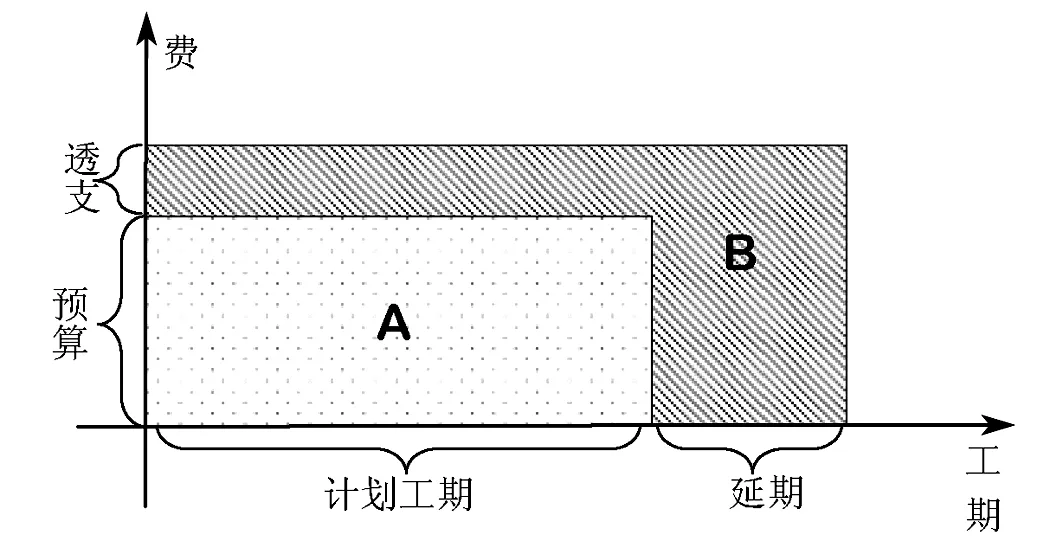
图1 设计风险分析图

项目工期持续期间，如果没有风险发生则整个项目会在计划工期和计划预算的控制范围内顺利完成，如图1中A部分所示。当由于某种原因在项目施工期间产生了设计风险元，项目中某个关键活动的结束时间被延迟，它的后继活动的开始时间也将会延迟，继而可能引发一系列的延迟问题。设计风险元也会造成已经完成的工程量进行返工，这时又产生了额外返工工程量。项目管理者会设法恢复原计划项目进度，但受实际施工能力的限制，往往是增加大量成本费用用于提升施工速度也很难达到期望的施工速度。如图1中B部分所示，项目实际完工时透支了预算，也造成了计划工期的延期。

1.2 系统因果分析

设计风险发生后，设计变更无论是由哪方提出，均应由监理部门会同建设单位、设计单位、施工单位等进行协商，经过确认后由设计部门进行设计变更，再下发到施工部门付诸实施。疑似设计风险元可能在剩余工程量中发生，也可能在已完成工程量中发生，或者在二者中都发生，发生的设计风险工程量后会有一个待批复延迟过程，在这个过程中会部分疑似设计风险工程量被驳回，不同意变更。被确认为设计风险工程量的部分在经过设计变更协商后只是部分确认为有变更的必要，最后设计单位的能力等因素不同又给设计工作造成不同程度的延迟。

设计变更后部分已完工工程量会进行返工导致建设材料需要调增；返工造成的工程量增加导致相应的施工费用也需要增加。设计风险工程量在审批、设计、返工过程中受前后工序等影响和实际施工速率限制不得不调整工期。加班问题已在文献[21]进行了研究，在此施工量增加时只考虑增加工期。

考虑到系统的边界性，本文设定设计变更后的工程量不再出现设计风险元，工程质量也都达到验收要求。设计风险元对项目的工期和费用影响过程因果关系如图2 所示。

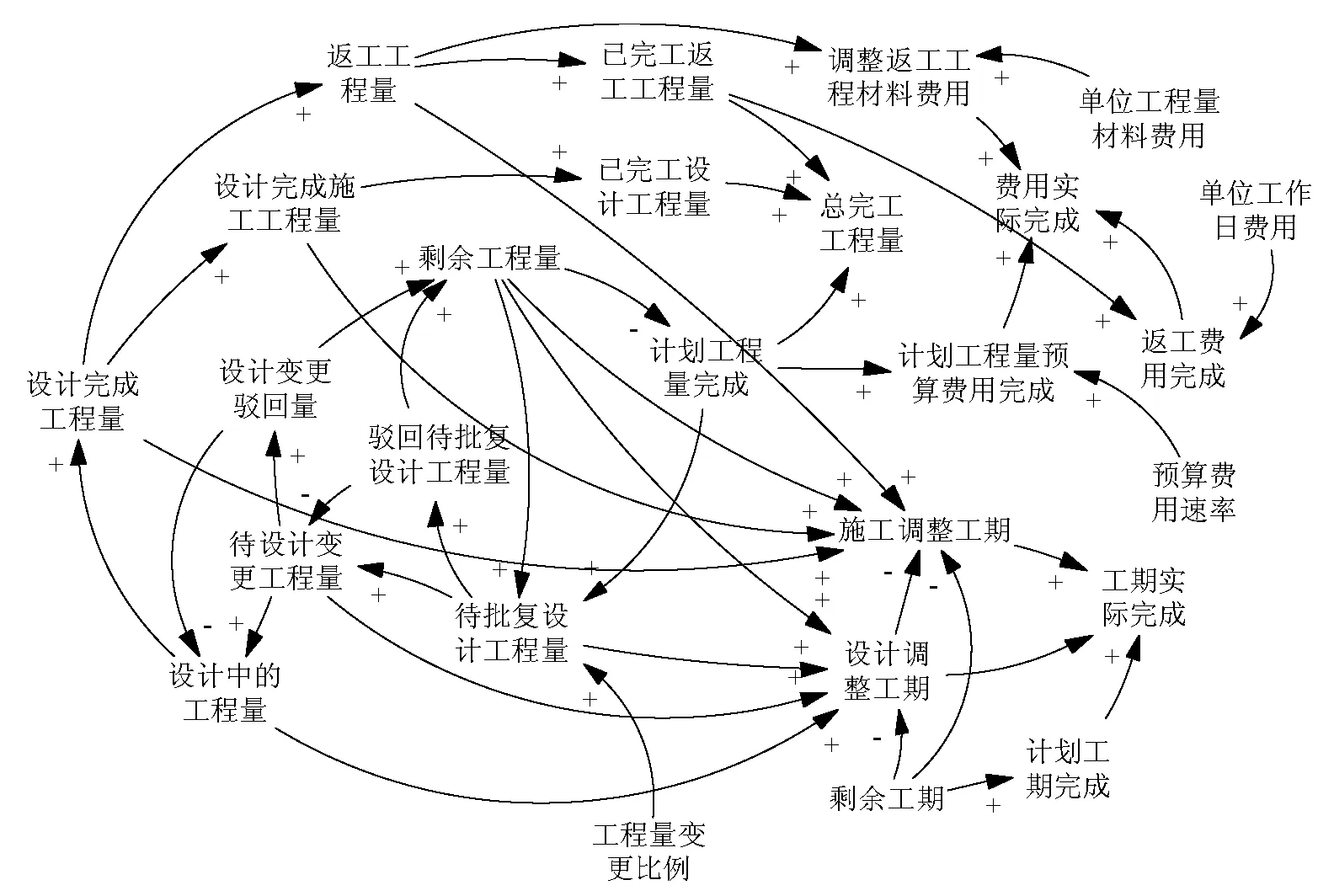
图2 设计风险因果分析图

2 系统动力学建模

根据上述分析，使用Vensim系统动力学软件建立设计风险元传递系统动力学模型，如图3所示。

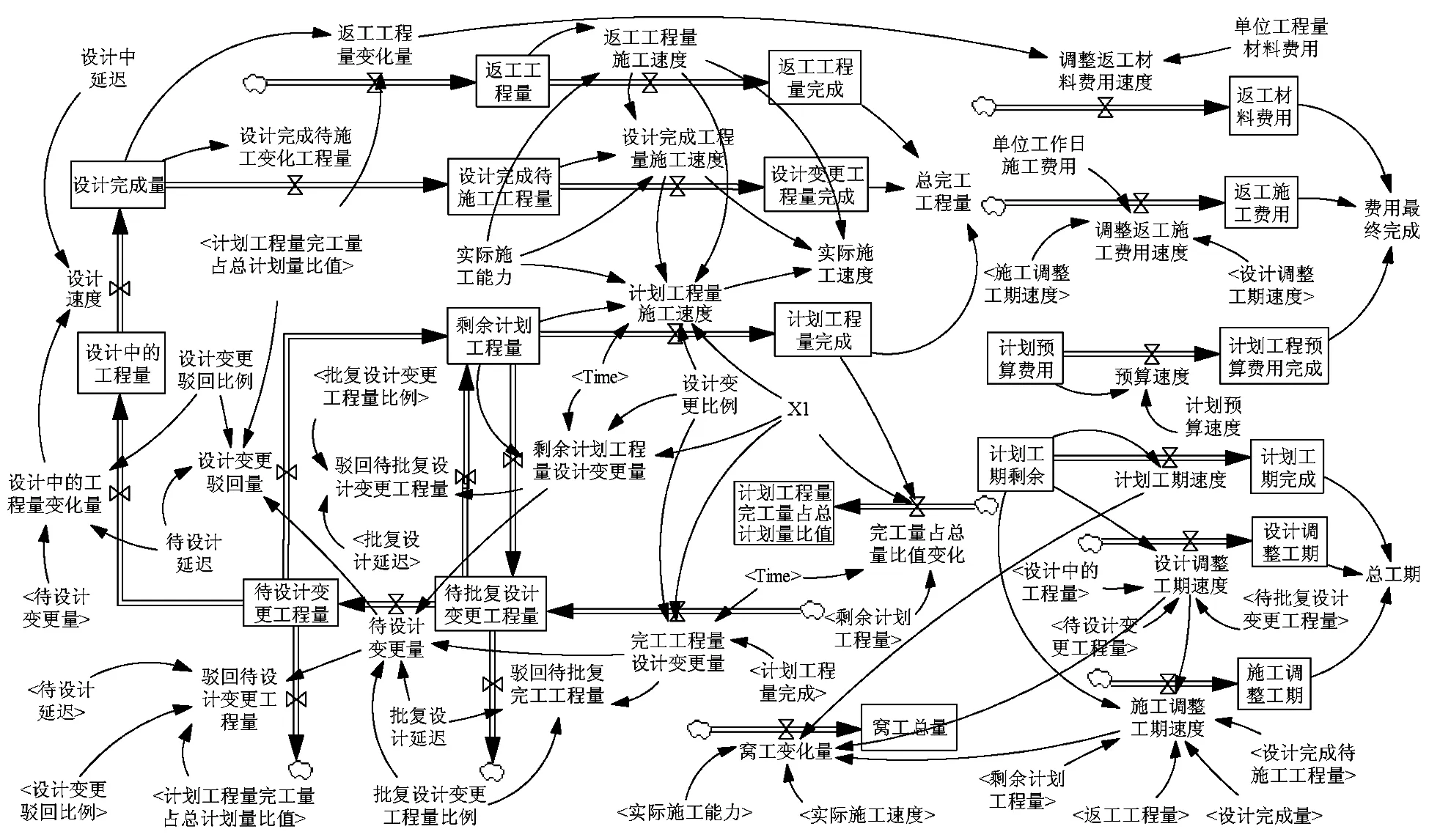
图3 设计风险流量图

此模型中由57个变量组成六个子系统：设计变更子系统、返工子系统、总完工工程量子系统、调整工期子系统、调整费用子系统、窝工总量子系统。

2.1 设计变更子系统

设计变更子系统的系统动力学模型如图3左下部分所示。在设计变更子系统中，设计风险元在X1时刻发生，经两级审批通过后进入设计过程中，驳回的工程量返回剩余计划工程量中，其中关系用如下公式表达：

剩余计划工程量设计变更量=IF THEN ELSE(X1=Time, IF THEN ELSE(剩余计划工程量<1,0,剩余计划工程量×设计变更比例),0)

(1)

驳回待批复设计变更工程量=DELAY FIXED(剩余计划工程量设计变更量×(1-批复设计变更工程量比例),批复设计延迟,0)

(2)

待批复设计变更工程量=INTEG(剩余计划工程量设计变更量+完工工程量设计变更量-待设计变更量-驳回待批复完工工程量-驳回待批复设计变更工程量, 0)

(3)

完工工程量设计变更量=IF THEN ELSE(X1=Time, IF THEN ELSE(计划工程量完成×设计变更比例<1,0,计划工程量完成×设计变更比例),0)

(4)

驳回待批复完工工程量=DELAY FIXED(完工工程量设计变更量×(1-批复设计变更工程量比例),批复设计延迟,0)

(5)

待设计变更量=DELAY FIXED((剩余计划工程量设计变更量+完工工程量设计变更量)×批复设计变更工程量比例,批复设计延迟,0)

(6)

驳回待设计变更工程量=DELAY FIXED(待设计变更量×设计变更驳回比例×计划工程量完工量占总计划量比值,待设计延迟,0)

(7)

待设计变更工程量=INTEG (待设计变更量-设计变更驳回量-设计中的工程量变化量-驳回待设计变更工程量, 0)

(8)

设计变更驳回量=DELAY FIXED(待设计变更量×设计变更驳回比例×(1-计划工程量完工量占总计划量比值),待设计延迟,0)

(9)

设计中的工程量变化量=DELAY FIXED(待设计变更量×(1-设计变更驳回比例),待设计延迟,0)

(10)

设计中的工程量=INTEG (设计中的工程量变化量-设计速度,0)

(11)

设计速度=DELAY FIXED(设计中的工程量变化量,设计中延迟,0)

(12)

计划工程量完工量占总计划量比值=INTEG(完工量占总量比值变化,0)

(13)

完工量占总量比值变化=IF THEN ELSE(X1=Time, IF THEN ELSE((剩余计划工程量+计划工程量完成)>0, 计划工程量完成/(剩余计划工程量+计划工程量完成),0),0)

(14)

公式中IF THEN ELSE(a,b,c)是系统动力学中表示条件的一个函数，其中a表示是条件，b和c分别表示条件成立和不成立时的变量取值。

公式中INTEL(d,e)是系统动力学中表示累积变化的一个函数，其中d表示变量的变化量，e表示变量的原始值。

公式中DELAY(f,g)是系统动力学中表示延迟的一个函数，其中f表示被延迟的变量，而g表示延迟时间。

2.2 返工子系统

返工子系统的系统动力学模型如图3左上部分所示。在设计变更完成后，已经完工的工程量部分需要返工，本模块为了便于量化分析工程量变化情况，上半部分考虑返工增加的那部分工程量，下半部分考虑与原计划工程量相同的那部分。其中关系用如下公式表达：

设计完成量=INTEG(设计速度-设计完成待施工变化工程量, 0)

(15)

设计完成待施工变化工程量=设计完成量

(16)

设计完成待施工工程量=INTEG(设计完成待施工变化工程量-设计完成工程量施工速度,0)

(17)

返工工程量变化量=设计完成量×计划工程量完工量占总计划量比值

(18)

返工工程量=INTEG(返工工程量变化量-返工工程量施工速度,0)

(19)

2.3 总完工工程量子系统

总完工工程量子系统的系统动力学模型如图3中上部分所示。受设计风险元影响，总完工工程量由原计划完工工程量、设计变更后完工工程量和完成返工工程量三部分组成。上述三种工程量的施工速度受实际施工能力所限，认定优先进行返工，其次进行设计变更后工程量施工，最后是原计划工程量施工。其中关系用如下公式表达：

返工工程量施工速度=MIN(返工工程量, 实际施工能力)

(20)

返工工程量完成=INTEG(返工工程量施工速度,0)

(21)

设计完成工程量施工速度=MIN(设计完成待施工工程量,实际施工能力-返工工程量施工速度)

(22)

设计变更工程量完成=INTEG(设计完成工程量施工速度,0)

(23)

剩余计划工程量=INTEG(设计变更驳回量+驳回待批复设计变更工程量-计划工程量施工速度-剩余计划工程量设计变更量,2500)

(24)

计划工程量施工速度=MIN(剩余计划工程量,实际施工能力-返工工程量施工速度-设计完成工程量施工速度)

(25)

计划工程量完成=INTEG(计划工程量施工速度,0)

(26)

总完工工程量=返工工程量完成+设计变更工程量完成+计划工程量完成

(27)

2.4 调整工期子系统

调整工期子系统的系统动力学模型如图3右下部分所示。设计批复和设计过程都需要时间处理，当原计划剩余工期小于设计批复和设计过程需要工期处理时就需要调整因设计原因导致的整个项目工期。原计划完工工程量、设计变更后完工工程量和完成返工程量三部分未全部完工时，如果所需的工期大于原计划剩余工期，就需要调整施工工期。其中关系用如下公式表达：

计划工期剩余=INTEG(-计划工期速度,50)

(28)

计划工期速度=MIN(计划工期剩余,1)

(29)

计划工期完成=INTEG(计划工期速度,0)

(30)

施工调整工期速度=IF THEN ELSE(计划工期剩余<1,IF THEN ELSE(设计调整工期速度<1,IF THEN ELSE(设计完成量>0:OR:设计完成待施工工程量>0:OR:返工工程量>0:OR:剩余计划工程量>0,1,0),0),0)

(31)

施工调整工期=INTEG(施工调整工期速度, 0)

(32)

设计调整工期速度=IF THEN ELSE(计划工期剩余<1,IF THEN ELSE(待批复设计变更工程量>0:OR:待设计变更工程量>0:OR:设计中的工程量>0, 1,0),0)

(33)

设计调整工期=INTEG(设计调整工期速度,0)

(34)

总工期=计划工期完成+施工调整工期+设计调整工期

(35)

公式中h:OR:i是系统动力学中表示“或”的计算符号，即当满足条件h或条件i之一时，其逻辑计算结果即为成立。

2.5 调整费用子系统

调整费用子系统的系统动力学模型如图3右上部分所示。已完工工程量重新设计变更后会产生返工工程量，需要增加施工材料。上述工期调整后，施工费用也需要相应调整。在发生设计风险元时，会产生实际施工速度小于实际施工能力的情况，但人员及设备等施工费用还是需要正常开支，原预算速率保持不变。因设计费占施工费用比例较小，不会对系统分析结果产生较大影响，在此不对设计费作深入研究。其中关系用如下公式表达：

调整返工材料费用速度=返工工程量变化量×单位工程量材料费用

(36)

返工材料费用=INTEG(调整返工材料费用速度,0)

(37)

调整返工施工费用速度=IF THEN ELSE(施工调整工期速度>0:OR:设计调整工期速度>0,单位工作日施工费用,0)

(38)

返工施工费用=INTEG(调整返工施工费用速度,0)

(39)

计划预算费用=INTEG(-预算速度,750000)

(40)

预算速度=IF THEN ELSE(计划预算费用<计划预算速度,计划预算费用,计划预算速度)

(41)

计划工程预算费用完成=INTEG(预算速度,0)

(42)

费用最终完成=计划工程预算费用完成+返工施工费用+返工材料费用

(43)

2.6 窝工总量子系统

窝工总量子系统的系统动力学模型如图3中下部分所示。在工期持续期间由于设计风险元导致部分工作量在审批或设计环节受到延迟，会发生实际施工速度小于实际施工能力的情况，在项目施工过程中窝工成本小于调迁成本或窝工成本在承受范围内不会调迁设备和人员，此子系统可以模拟出窝工总量。其中关系用如下公式表达：

窝工变化量=IF THEN ELSE(计划工期速度>0:OR:施工调整工期速度>0:OR:设计调整工期速度>0,实际施工能力-实际施工速度,0)

(44)

窝工总量=INTEG(窝工变化量, 0)

(45)

实际施工速度= 计划工程量施工速度+设计完成工程量施工速度+返工工程量施工速度

(46)

3 模型算例分析

3.1 参数设置说明

模型中部分参数设置如表1所示，其中比例参数是经验值，根据不同项目类型或管理机制可作适当调整，不影响此模型的鲁棒性和分析准确性。

表1 参数设置表

3.2 模拟与分析

(1)模拟没有设计风险元发生时，即工程量设计变更比例为0时的情况，如图4所示。项目共进行了50天(线1)，在此期间：总费用为75万元，曲线匀速上升(线3)；剩余工程量(线2)匀速下降，总完工工程量2500个单位。

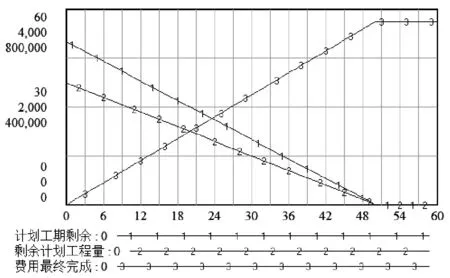
图4 无风险模拟结果图

(2)模拟设计风险元在施工到第20天时发生，工程量设计变更比例设为1时，其中设计时间为2天的情况，如图5所示。项目共进行了73天，由于施工原因调整工期23天，在此期间：总完工工程量3480个单位，返工490个单位，设计后重新施工1225个单位，原计划工程量完成1765个单位；总费用为93.66万元，材料费用调增11.76万元，施工费用调整6.9万元。

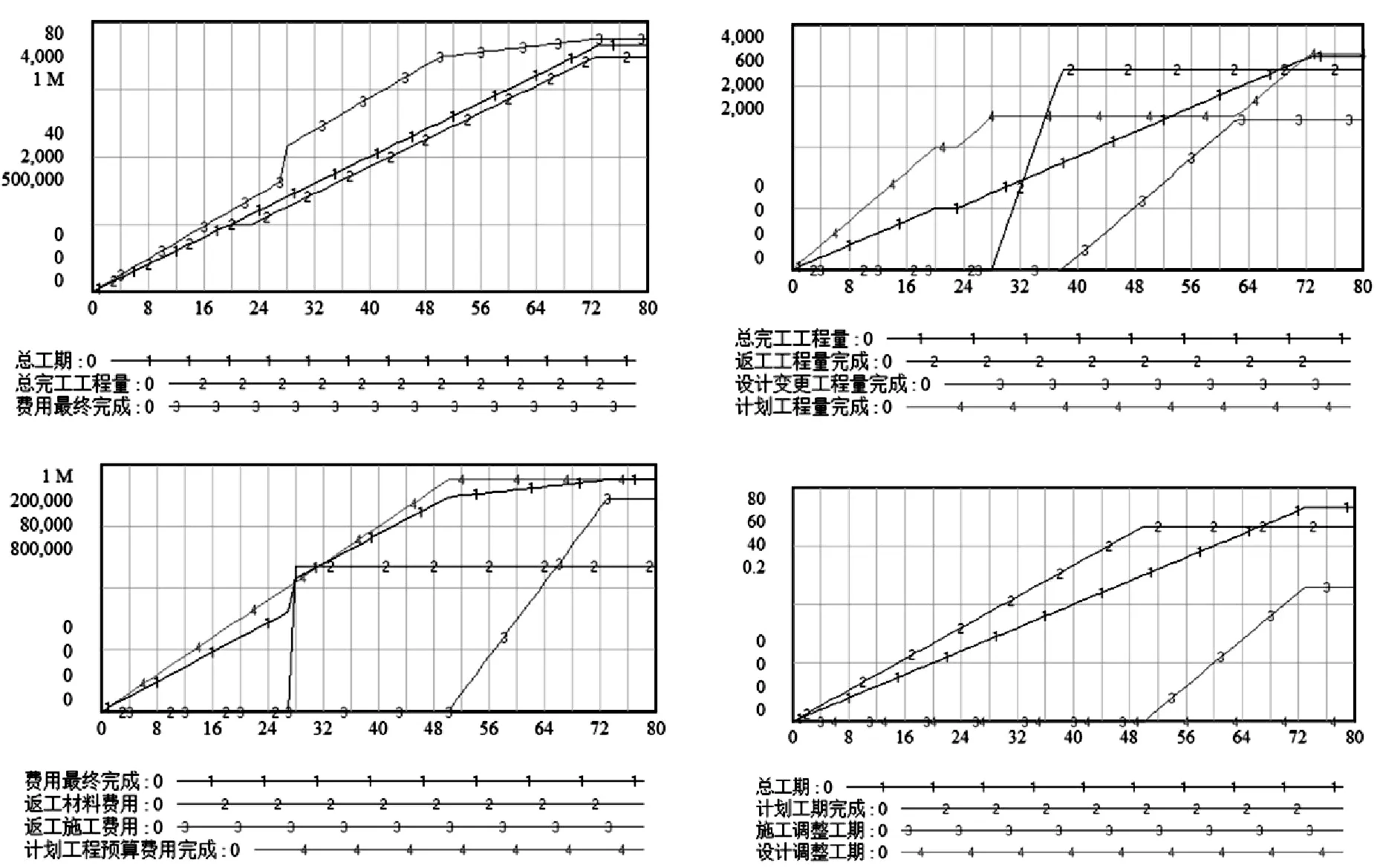
图5 第20天设计变更比例为1，设计时间为2天的模拟结果图

(3)模拟设计风险元在施工到第49天时发生，工程量设计变更比例设为1时，其中设计时间为10天的情况，如图6所示。项目共进行了114天，由于施工原因调整工期50天，设计审批及设计时间为14天，在此期间：总完工工程量4901个单位，返工1200.5个单位，设计后重新施工1225个单位，原计划工程量完成2475.5个单位；总费用为123.01万元，材料费用调增28.81万元，施工费用调整19.2万元。

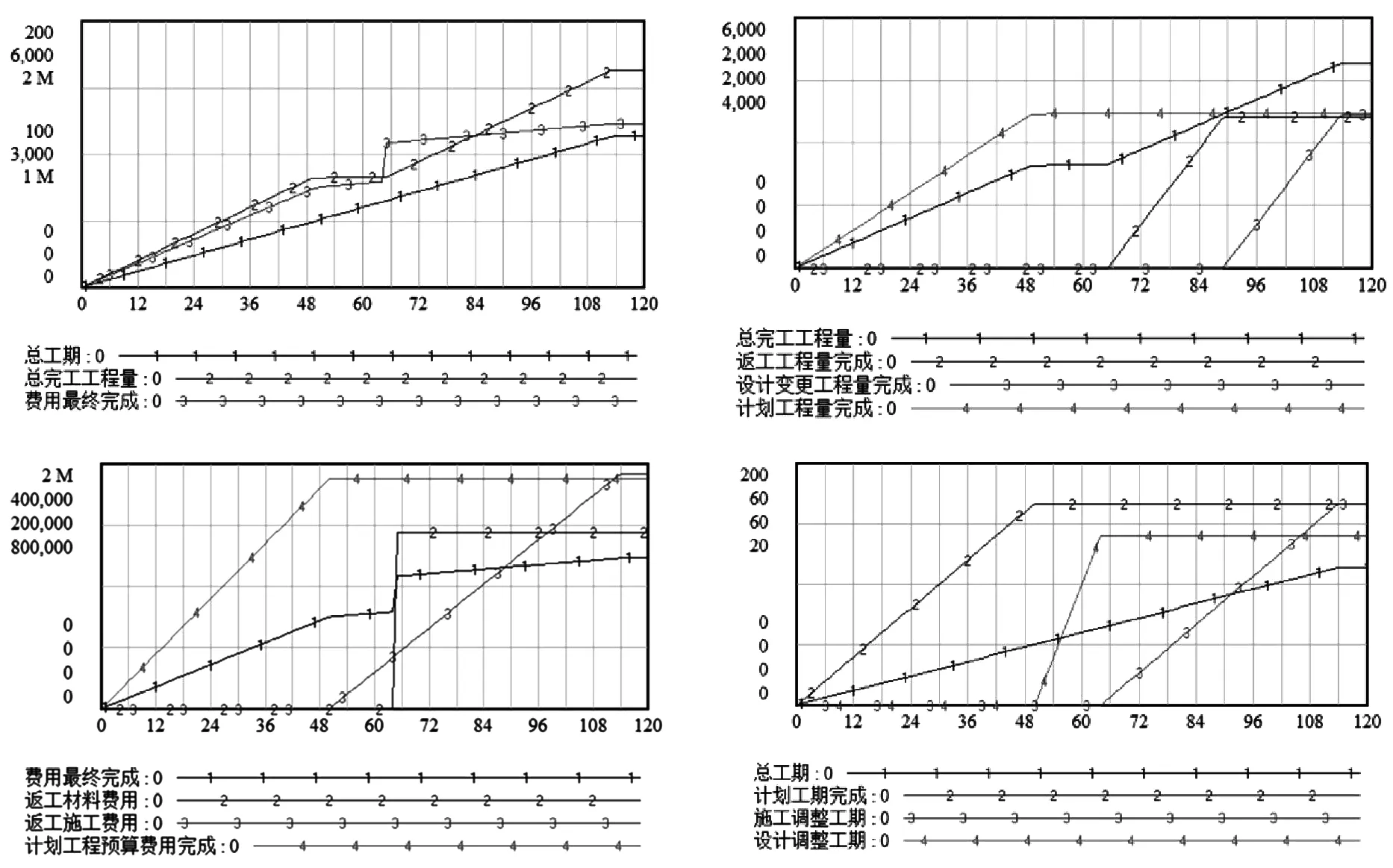
图6 第49天设计变更比例为1，设计时间为10天的模拟结果图

由于篇幅所限，其他模拟结果数据见表2所示。

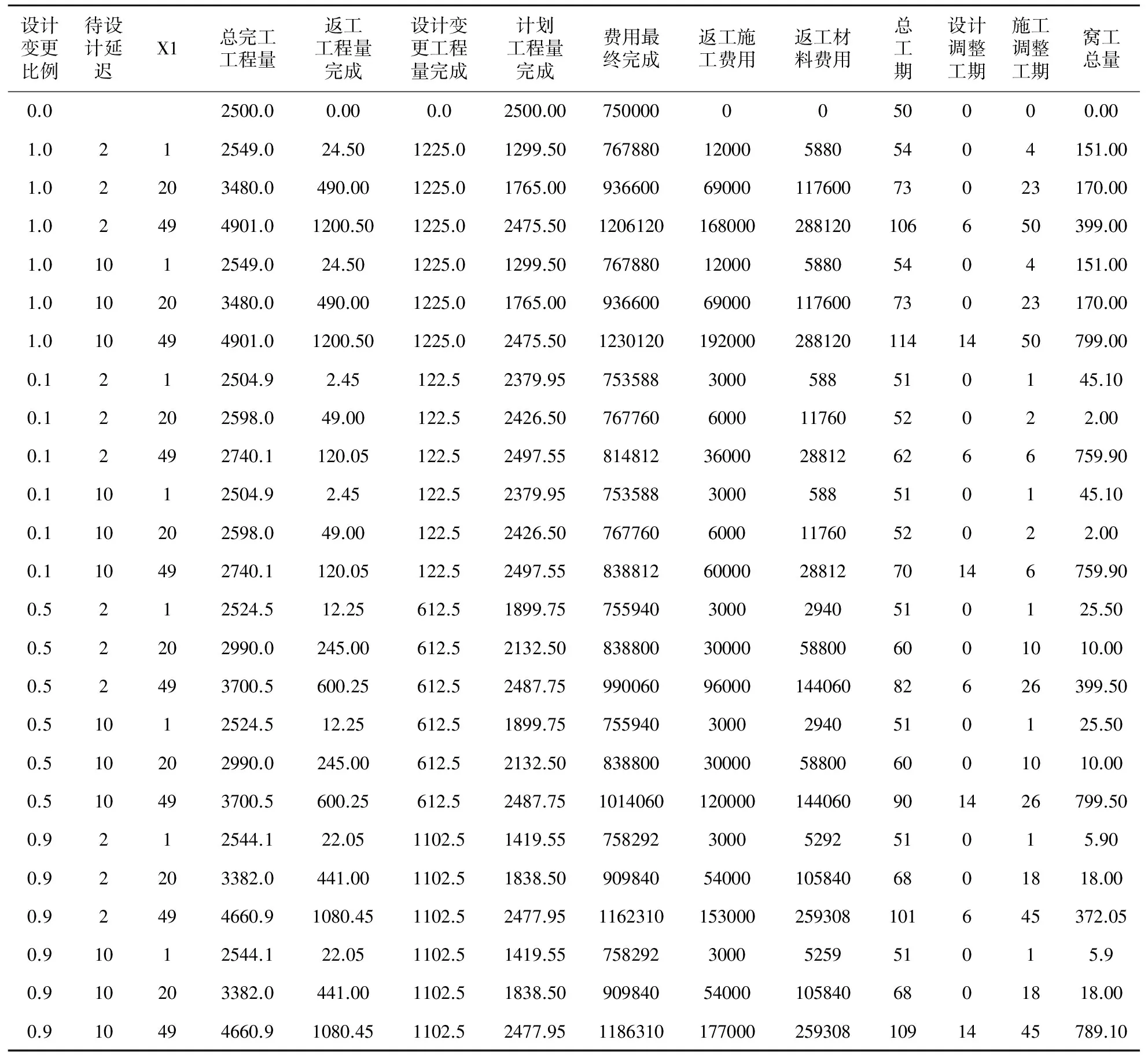
表2 其他模拟结果

4 结论

项目在施工过程中产生设计风险元，经过传递会对项目的工程量、费用及工期产生影响，本文建立了相应的风险元传递系统动力学模型，对项目的影响范围及深度进行模拟，通过模拟得出以下几方面的结论:

(1)用系统动力学模型将风险元传递理论引入到设计变更对施工项目的影响传递过程中，可以量化分析其影响过程及深度。

(2)设计风险元发生时间越晚原计划工程量完工就越多，返工工程量增加越大；工程返工需要施工材料增多，购买材料费用也需要追加；返工工程量对应的施工费用和工期也需要增加。

(3)设计风险元发生的时间加上设计审批时间及设计时间大于剩余工期时，设计审批及设计过程会影响工期调增。

(4)因设计审批和设计过程中部分工程量不能施工，使得实际施工速度低于施工能力，造成施工量不饱和形成窝工。

(5)设计变更比例值不同，对工期、材料费用、施工费用影响程度不同。

有待进一步研究的内容包括：同一项目中多次叠加设计风险元发生的传递过程及影响情况；设计能力和设计审批流程影响到设计时限，对工期产生影响程度；设计风险元对施工材料的浪费情况。

[1] Han S. A hybrid simulation model for understanding and managing non-value adding activities in large-scale design and construction projects[D]. Illinois: University of Illinois at Urbana-Champaign, 2008.

[3] Hagen E W, Mays G T. Human factors engineering in the US nuclear arena[J]. Nuclear Safety, 1981, 22(3): 337-346.

[4] Love P E, Lopez R, Edwards D J, Goh Y M. Error begat error: design error analysis and prevention in social infrastructure projects[J]. Accident Analysis & Prevention, 2012, 48: 100-110.

[5] Fayek A R, Dissanayake M, Campero O. Measuring and classifying construction field rework: a pilot study[J]. Canadian Journal of Civil Engineering, 2003, 31(6): 1077-1089.

[6] 张尧，陈曦，刘洋，樊治平.考虑两个风险情形的项目风险应对策略选择方法[J].运筹与管理,2014,23(3)：252-256.

[8] Rounce G. Quality, waste and cost considerations in architectural building design management[J]. International Journal of Project Management, 1998,16(2): 123-127.

[9] Love P E D, Edwards D J, Han S, Goh Y M. Design error reduction: toward the effective utilization of building information modeling[J]. Research in Engineering Design, 2011,22(3):173-187.

[11] 邵等玲.工程项目设计风险控制[J].铁路工程造价管理,2009,24(3):25-28.

[12] 徐晓兵，苏永强，周剑波.建筑工程设计风险评价方法的研究[J].华北科技学院学报,2009,6(4):112-114.

[13] 方俊.建设项目工程变更控制研究[D].重庆：重庆大学,2005.

[14] 季国良.设计变更工程项目中工程量变化对造价的影响[J].中国市政工程,2008,(6):57-58.

[15] 李存斌，李鹏，陆龚曙.基于MFGM企业项目链风险元传递研究[J].运筹与管理,2013,(4):241-247.

[16] 李存斌.项目风险元传递理论及应用[M].北京:中国水利水电出版社,2009.

[17] 周昌发.企业应收款法律风险防范体系构建研究[J].中国软科学,2013,(10):186-192.

[18] Forrester J W. Industrial dynamics[M]. MIT Press: Cambridge, MA, 1961.

[19] 姜钰，贺雪涛.基于系统动力学的林下经济可持续发展战略仿真分析[J].中国软科学,2014(1):105-114.

[20] Wang Q F, Ning X Q, You J. Advantages of system dynamics approach in managing project risk dynamics[J]. Journal of Fudan University (Natural Science), 2005, 44(2): 201-206.

[21] 李存斌，陆龚曙. 工程项目风险元传递的系统动力学模型[J].系统工程理论与实践,2012,32(12):2731-2739.

Study on Model of Design Risk Element Transmission in the Construction Project

LI Cun-bin, LIU Yun-qi, LI Shu-ke

(SchoolofEconomicsandManagement,NorthChinaElectricPowerUniversity,Beijing102206,China)

Design risk is one of the main reasons for leading to rework in the process of the construction. In this paper, based on the generic project risk element transmission theory and system dynamics, a system dynamics model of construction project design risk element transmission is developed. The factors leading to the quantity increase of construction projects are considered as design risk element, and after the analysis of transfer process of design risk element in construction project, a corresponding causal feedback loop is constructed. By assigning values to model variables and establishing functions between them, the model is simulated through software Vensim. The results indicate that design risk element exerts different degree of influence on project cost and time, and that the more design risk element occurs or the later design risk element occurs, the faster will the impact accelerate through the internal structure of project. In addition, it can be concluded that the model results chart, which reflects the dynamic changes of individual construction project, can provide sound evidence for risk management and project management.

project management; design risk; risk element transmission; system dynamics

2014-10-10

国家自然科学基金资助项目(71271084,71071054)；中央高校基本科研业务费专项资金资助(2014XS55,2015XS32)；北京市产学研联合培养研究生基地项目

李存斌(1959-)，男，硕士，教授，博士生导师，研究方向：信息管理、项目风险管理;刘赟奇(1979-)，男，博士研究生，研究方向：项目管理、风险管理;李书科(1978-)，女，博士研究生，研究方向：风险管理、信息管理。

C931；N949

A

1007-3221(2015)06- 0143- 09

10.12005/orms.2015.0206