考虑相互依赖性的信息系统安全投资及协调机制

顾建强， 梅姝娥， 仲伟俊

(东南大学 经济管理学院，江苏 南京 211189)



考虑相互依赖性的信息系统安全投资及协调机制

顾建强， 梅姝娥， 仲伟俊

(东南大学 经济管理学院，江苏 南京 211189)

考虑信息系统安全相互依赖情形下最优化信息系统连续时间安全投资水平是一个值得研究的问题。首先讨论了非合作博弈下信息系统安全投资的最优策略选择，在此基础上讨论了安全投资效率参数、黑客学习能力、传染风险对信息系统脆弱性及信息系统安全投资率的影响。其次，在推导出两企业在合作博弈情形下最优策略选择的基础上，对比两种情形下的博弈均衡结果，得出合作博弈下的投资水平高于非合作博弈下的投资水平。原因是两个企业的相互依赖关系隐含着企业投资的负外部性，从而导致企业投资不足。最后，构建一种双边支付激励机制消除企业投资不足问题，从而使企业达到合作博弈下的最优投资水平，提高两个企业的收益。

信息系统安全投资；合作协调；微分博弈；相互依赖的安全

0 引言

随着计算机网络的快速发展，通过运用先进的信息技术来联系关联企业和整合供应链正成为各个行业的趋势，如Electronic Data Interchange(EDI) ，Continuous Replenishment Program(CRP)and Vendor Managed Inventory(VMI)等技术的广泛运用使得企业与其上下游企业、甚至与竞争对手之间形成了紧密的联系和信息共享[1]。一个企业信息系统的安全性直接影响关联企业信息系统的安全性[2,3]。如果关联企业安全水平不高，共享信息不能得到有效的保护，则企业提升自身信息系统安全性付出的代价必然会提高[4]。考虑信息系统安全相互依赖性背景下的企业信息系统安全投资策略，是信息系统安全投资研究领域的重点问题之一。目前，关于这方面的研究已经有了不少文献。Kunreuther和Heal运用博弈论研究了存在信息系统安全相互依赖性的企业之间安全投资上的纳什均衡，发现在非合作条件下，可能存在投资不足的问题，并分析了保险、责任、罚款和补贴、第三方检查、规章和协调等外部机制对信息系统安全投资的影响[5]。Garcia和Horowitz通过建立博弈论模型分析得出对于相互竞争的多个企业，从最大化社会福利的角度看每个企业的信息系统安全投资水平都偏低，所以有必要通过补贴提高企业的安全投资水平[6]。Zhuang等通过建立信息系统安全模型并通过分析指出，在多个企业信息系统相互关联的情况下，缺乏战略视角企业的存在使得其他企业不愿意进行安全投资[7]。Zhang进一步指出，企业信息系统相互关联的情况下，为某些企业提供信息系统安全补助，能够提升社会最优安全投资均衡的稳定性，提高社会福利[8]。Bandyopadhyay等以网络供应链为背景，讨论了网络脆弱性和供应链整合程度对企业信息系统安全投资的影响。他们发现，即使这两种因素对企业信息系统安全风险产生相同的影响，但对企业的安全投资却有不同的影响[9]。

仔细研读以上文献，可以看出现有的文献都是从静态角度分析企业的信息系统安全投资策略。但是当企业信息系统的脆弱性，黑客的学习能力等表现为随时间动态变化的时候，这些特征不能很完美地通过静态模型体现出来，导致结果与现实产生一定的差距。因此，鉴于信息系统安全的背景环境的复杂性和动态变化的特点[11]，在动态框架下研究信息系统安全投资更加贴近现实。因此本文考虑的是企业信息安全相互依赖情形下两个企业信息系统安全投资问题。通过建立微分博弈模型探讨了两企业合作博弈和非合作博弈时的最优行动选择，通过对两种情形下的博弈均衡结果进行分析和对比，得到实现合作解的激励机制。期望所得到的相关结论能为企业在信息系统安全投资、多企业合作机制等方面的科学决策提供理论依据。

1 基本假设与描述

本文从最简单的模型开始，只考虑属于入侵目标集的两个信息系统安全关联的企业(i,j)。黑客的目标是通过病毒直接入侵或者间接入侵(即通过病毒侵入其他企业，再通过企业之间的信息系统互联而传播)信息资产以期达到一定的经济收益[12]。为了保护企业的信息系统安全，需要通过安全投资来减少信息系统的脆弱性，从而降低病毒成功入侵的概率，以期减少企业的损失。

变量和参数说明

Pi，Pj状态变量，分别表示两个企业信息系统的脆弱性水平，0⩽Pi，Pj⩽1Li，Lj分别表示病毒成功入侵给企业带来的损失q病毒传播给另一个企业的概率Si，Sj控制变量，分别表示两个企业信息系统安全投资率r贴现率β投资效率参数ρ黑客的学习效应对企业信息系统脆弱性的影响

假设1 考虑计算机病毒传播的情形，即如果一个企业的信息系统被病毒感染，病毒就会有可能传播给另外的关联企业。这种情况下，单个企业的全部成本依赖于其双方的脆弱性水平和自身的安全投资。

即企业i的期望成本为Ci=(1-(1-Pi)(1-qPj))Li+Si。

假设2 每个企业信息系统的脆弱性由企业信息系统安全投资量来决定，且信息系统的脆弱性是一个动态变化的过程，可以用式(1)所示的微分方程来表示信息系统脆弱性的变化过程：

(1)

假设3 为了确保系统能达到稳定状态，假设黑客的学习效应低于信息系统安全投资的影响效应，即βS(t)>ρ。

假设4 根据文献[9],假设信息系统被病毒成功入侵并传染的概率小于1/2，即qP<1/2。

2 非合作安全投资博弈

非合作博弈中，两个企业处于分散决策情形, 双方同时且独立确定自己的最优投资策略。其均衡为反馈Nash均衡。

在该种情况下，两个企业的目标函数分别为：

(2)

(3)

现值哈密尔顿函数表示企业从信息系统安全投资中取得的全部收益(包括当前的和未来的收益)，根据状态方程(1)和目标方程(2)(3)，可以得到两企业的哈密尔顿函数为：

Hi=-(1-(1-Pi)(1-qPj))Li-Si+λii(-βiSi(t)Pi+ρ)+λij(-βjSj(t)Pj+ρ)

(4)

HJ=-(1-(1-Pj)(1-qPi))Lj-Sj+λji(-βiSi(t)Pi+ρ)+λjj(-βjSj(t)Pj+ρ)

(5)

(4)(5)中的λii,λij,λji,λjj表示伴随变量，度量企业信息系统脆弱性的单位量改变对未来收益的现值影响，受以下条件控制：

(6)

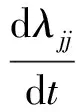
(7)

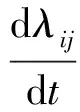
(8)

(9)

从(4)(5)可以看出，哈密尔顿函数对控制变量(Si和Sj)是线性的，从而可以得出(10)式解。

(10)

奇异解由以下条件得到：

(11)

(12)

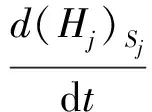
(13)

结合(6)～(13)和(1)，我们得到

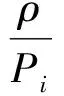
(14)

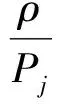
(15)

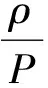
定理1 在奇异域和对称情形下，两个企业投资为相同的不变值，当信息系统安全投资效率(β)下降，或者传染率(q)、黑客学习能力(ρ)上升时，信息系统脆弱性(P)上升。当黑客学习能力(ρ)上升时，信息系统安全投资率(S)上升。当qβP3L>ρ时，信息系统安全投资效率(β)上升时，信息系统安全投资率(S)上升，反之，信息系统安全投资率(S)下降。当传染率(q)上升时，信息系统安全投资率(S)下降。

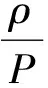
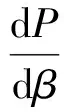
投资效率参数(β)表明企业通过信息系统安全投资来降低信息系统脆弱性的能力。更高的信息系统安全投资效率参数(β)表示企业的信息系统安全投资有更高的效率和更高的信息系统安全投资收益。因此，投资效率参数(β)比较高的情况下，低一点的投资率也可以维持高的信息系统安全水平。但是值得注意的是，投资效率参数(β)上升，企业信息系统安全投资率(S)并不是总是上升的，只有当qβP3L>ρ时，两者才是正相关的。黑客学习能力(ρ)上升时，企业的反应是通过更高的投资率来维持原来的安全水平，但是由于边际收益递减效应的影响，会导致企业信息系统安全水平下降。作为黑客学习能力的上升的结果，企业投资更多，但信息系统脆弱性反而更高。传染率(q)上升，企业受到间接攻击的可能性增大，负外部性增大，因此投资动力不足，表现为信息系统安全投资率下降。

在不对称情形下，两企业有不同价值的信息资产需要保护(在这里仍然假设βi=βj=β)。由(14)～(15)可得

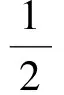
(16)

定理2 在奇异域下，当两个企业有相同的信息系统安全投资效率(βi=βj=β)，资产价值高的企业信息系统脆弱性要比资产价值低的企业信息系统脆弱性低。

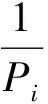
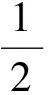
因为两个企业有相同的投资效率参数，他们的每单位成本投资效率可以直接进行比较。在这种情况下，黑客成功入侵给企业带来的损失更高的企业一定在信息系统安全防御上投资更多。即相对于其他企业，其维持更低的信息系统脆弱性。

3 合作博弈

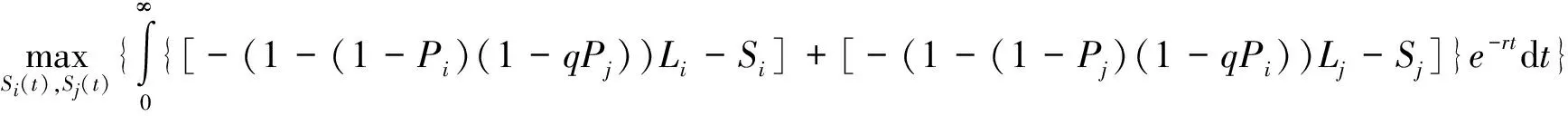
(17)

现值哈密尔顿函数为：

Hc= -(1-(1-Pi)(1-qPj))Li-Si-(1-(1-Pj)(1-qPi))Lj

-Sj+λci(-βiSi(t)Pi+ρ)+λcj(-βjSj(t)Pj+ρ)

λci,λcj表示伴随变量，度量企业信息系统脆弱性的单位量(Si,Sj)改变对整体未来收益的现值影响。哈密尔顿函数对控制变量(Si和Sj)是线性的，因此我们仍然得到一个关于Si,Sj的bang-bang解和奇异解形式。同样的，可以得到奇异域的两个方程：

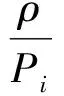
(18)

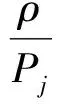
(19)

在对称条件下，同样可推得

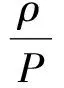
(20)

定理3 相对于非合作博弈，在合作博弈情形下，两对称企业分别维持更高的信息系统安全投资率。

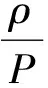
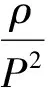
推出PD≥PC,进一步推出SD≤SC。

在非合作博弈情形下，如果企业i的信息系统安全投入增加，那么病毒成功入侵企业i的可能性就比较小，同时从攻击企业i信息系统转而攻击企业j信息系统的概率就会减少。但是在非合作情况下，企业在进行投资时不会考虑增加投资给其他企业带来的正外部性影响，所以相对于合作情形下，非合作情况下两对称企业信息系统安全投资不足。

4 合作协调机制

合作决策能够使两个企业在信息系统安全投资方面节约成本。因此，有必要通过一定的机制来激励双方实现合作解。一个可行的方法是通过强加一项双边支付机制来影响企业的信息系统安全投资水平，从而能够解决投资不足的问题。

考虑这样一个支付机制：企业I支付φi(Pi)给企业J，φi(Pi)是关于企业I信息系统脆弱性的一个函数。同样的，企业J支付φj(Pj)给企业I，φj(Pj)是关于企业信息系统脆弱性的一个函数。因此，两个企业的目标函数可以表现为以下形式：

(21)

(22)

两企业的哈密尔顿函数为：

Hi=-(1-(1-Pi)(1-qPj))Li-Si-φi(Pi)+φj(Pj)+λii(-βiSi(t)Pi+ρ)+λij(-βjSj(t)Pj+ρ)

(23)

Hj=-(1-(1-Pj)(1-qPj))Lj-Sj-φj(Pj)+φi(Pi)+λji(-βiSi(t)Pi+ρ)+λjj(-βjSj(t)Pj+ρ)

(24)

仍然得到一个关于Si,Sj的bang-bang解和奇异解形式。同样的，可以得到奇异域的两个方程：

(25)

(26)

在对称情况下，Li=Lj=L,βi=βj=β，Pi=Pj=P，因此方程简化为

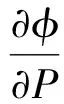
(27)

利用(20)，可以得到

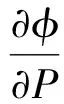
(28)

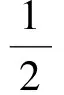
这时候，两个对称企业的目标函数变为以下形式：

(29)

(30)

在非合作博弈下，新的目标函数下的均衡结果和合作下的结果是一样的。换句话说，在应用的上述的补偿计划后，两个企业避免了投资不足的问题。然而，这个补偿计划的实现需要有一个双方都认可的第三方对两企业的信息系统安全水平进行检查，以确保补偿基于双方企业真实的信息系统脆弱性水平。

5 数值分析

两个企业在在合作与非合作信息系统安全投资博弈情形下，信息系统的脆弱性和利润依赖模型中参数的选择，假定取Li=Lj=100，r=0.5，ρ=0.6，βi=βj=1，q=0.1,0.2,0.3,0.4，则两个企业在在合作与非合作信息系统安全投资博弈情形下，其信息系统的脆弱性和合作协调下的支付补偿如表1所示。

表1 非合作与合作下的信息系统的脆弱性和协调支付补偿额

从表1中可看出，两个企业在合作情形下的信息系统脆弱性低于非合作情形下的信息系统脆弱性，这与理论推导相符。而且两种情形下信息系统脆弱性的差距以及合作协调下的支付补偿额随着传染率q的增大而增加。说明相互依赖性越大越能体现合作协调的价值。

6 结语

应用微分博弈的方法研究了两个企业在面对黑客病毒攻击下的信息系统安全投资过程，主要得到以下结论：①病毒传播攻击使两个企业在信息系统安全方面进行投资不足；②合作博弈能够使企业在信息系统安全方面增加投资；③在非合作情形下，可以通过一个双方的合理的补偿计划来激励企业达到合作情形下的均衡水平。有以下几个创新点：一是主要研究了动态情况下的投资策略。加入时间维的微分博弈模型分析企业的信息系统安全投资策略，更能体现鉴于信息系统安全的背景环境动态变化的特点，因而更加贴近现实情况。二是提出了在非合作情形下，如何通过一种双边支付机制来达到合作情形下的均衡水平。未来可进一步研究两个以上企业之间的病毒入侵情形下的信息系统安全投资或者可以设计实现多企业面对网络病毒入侵情形下协调的补偿机制，以及考虑多企业博弈下，在非对称情形时如何激励以达到总体最优。

[1] Mukhopadhyay T, Kekre S, Kalathur S.Business value of information technology: a study of electronic data interchange[J]. MIS Q, 1995, 19(2): 137-155.

[2] Gordon L A, Loeb M P,Lucyshyn W, Sharing information on computer system security: an economic analysis[J]. Journal of Accounting and Public Policy, 2003, 22(9): 461- 485.

[3] 吕俊杰,邱菀华,王元卓.基于相互依赖性的信息安全投资博弈[J].中国管理科学,2006,14(3)：7-12.

[4] Hausken K. Income, interdependence, and substitution effects affecting incentives for security investment[J]. Journal of Account Public Policy, 2006, 25(6): 629- 665.

[5] Kunreuther H, Heal G. Interdependent security[J]. Journal of Risk and Uncertainty, 2003, 26(2), 231-249.

[6] Garcia A, Horowitz B. The potential for underinvestment in internet security: implications for regulatory policy[J]. Journal of Regulatory Economics, 2007, 31(1): 37-55.

[7] Zhuang J, Bier V M, Gupta A. Subsidies in interdependent security with heterogeneous discount rates[J]. The Engineering Economist, 2007, 52(1): 1-19.

[8] Zhuang J. Impacts of subsidized security on stability and total social costs of equilibrium solutions in an n-player game with errors[J]. The Engineering Economist, 2010, 55(2): 131-149.

[9] Bandyopadhyay T, Jacob V, Raghunathan S. Information security in networked supply chains: impact of network vulnerability and supply chain integration on incentives to invest[J]. Information Technology and Management, 2010, 11(1): 7-23.

[10] Hausken K. Information sharing among firms and cyber attacks[J]. Journal of Accounting and Public Policy, 2007, 26(6): 639- 688.

[11] Mookerjee V, Mookerjee R, Bensoussan A, Yue W T. When hackers talk: managing information security under variable attack rates and knowledge dissemination[J]. Information Systems Research, 2011, 22(3): 606- 623.

[12] Png I P L, Wang Q. Information security: user precautions vis-à-vis enforcement against attackers[J]. Journal of Management Information Systems, 2009, 26(2): 97-122.

[13] Cremonini M, Nizovtsev D. Risks and benefits of signaling information system characteristics to strategic attackers[J]. Journal of Management Information Systems, 2009, 26(3): 241-274.

Dynamic Coordination Mechanism of Information System Security Investment Based on Interdependent Security

GU Jian-qiang, MEI Shu-e, ZHONG Wei-jun

(SchoolofEconomicsandManagement,SoutheastUniversity,Nanjing211189,China)

Optimizing continuous time information system security investment decisions of firms in the case of interdependent security is worthing studying. First, we employ the methodology of differential games to investigate two firms’ optimal investment strategies in the Nash non-cooperative game. In this general non-cooperative information system security investment game situation，the influence on the equilibrium vulnerability (security investment rate)is studied when three important elements(investment efficiency parameter,hackers’ learning effect, pidemic risk)are changed .Then the optimal action selection of two partners in the cooperative game situation is analyzed. After comparing these two game equilibrium results，it is found that symmetric firms maintain a higher rate of security investment under cooperative situation. The application of executing a bilateral compensation scheme is one of the measures to achieve the equilibrium which under coordination.

information system security investment; coordination; differential game; interdependent secuurity

2013-12-12

国家自然科学基金资助项目(71071033)

顾建强(1979-)，男，江苏泰州人，博士研究生，研究方向：信息系统安全投资策略及风险管理；梅姝娥(1968-)，女，江苏南通人，博士生导师，教授，研究方向：信息安全经济学，决策理论；仲伟俊(1962-)，男，江苏南通人，博士生导师，教授，研究方向：信息管理与信息系统。

TP309

A

1007-3221(2015)06- 0136- 07

10.12005/orms.2015.0205